22.1 平行四边形的性质 第1课时 课件(共17张PPT) 冀教版八年级下册
文档属性
| 名称 | 22.1 平行四边形的性质 第1课时 课件(共17张PPT) 冀教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
22.1 平行四边形的性质
第1课时
第二十二章 四边形
学习目标
1、理解平行四边形的概念;
2、探索并证明平行四边形的性质定理1.
学习重难点
探索并证明平行四边形的性质定理1.
探索并证明平行四边形的性质定理1.
难点
重点
创设情境
在我们的周围存在着许多的四边形. 观察下列图片,从中找出四边形,并就它们的共同特性和不同特性,和大家交流一下你的看法
新知引入
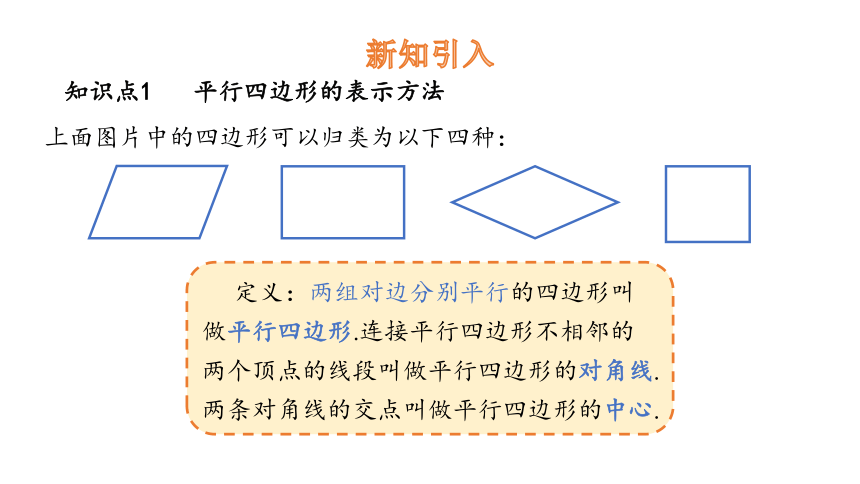
知识点1 平行四边形的表示方法
上面图片中的四边形可以归类为以下四种:
定义:两组对边分别平行的四边形叫做平行四边形.连接平行四边形不相邻的两个顶点的线段叫做平行四边形的对角线.两条对角线的交点叫做平行四边形的中心.
如图,四边形ABCD是平行四边形,记作“ ABCD”,读作“平行四边形ABCD”.线段AC,BD为 ABCD的两条对角线,点O为它的中心.
A
D
C
B
O
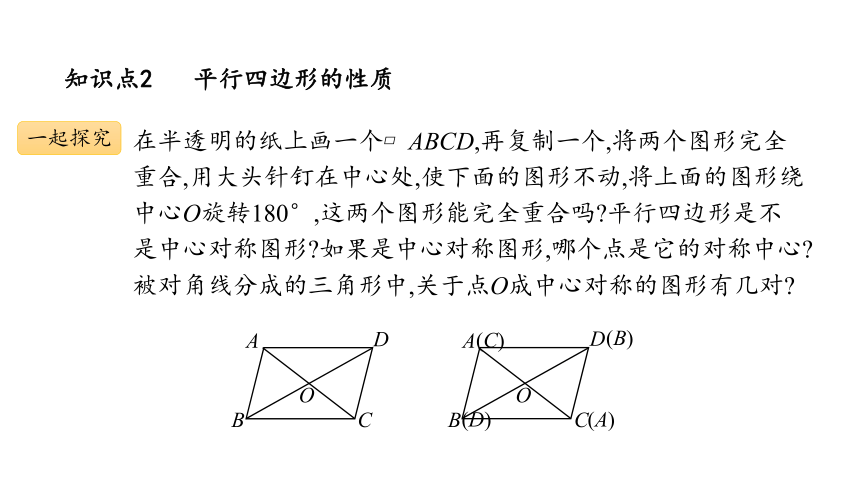
知识点2 平行四边形的性质
在半透明的纸上画一个 ABCD,再复制一个,将两个图形完全重合,用大头针钉在中心处,使下面的图形不动,将上面的图形绕中心O旋转180°,这两个图形能完全重合吗 平行四边形是不是中心对称图形 如果是中心对称图形,哪个点是它的对称中心 被对角线分成的三角形中,关于点O成中心对称的图形有几对
A
D
C
B
O
A
D
C
B
O
(C)
(B)
(A)
(D)
一起探究
2. 在上面的活动过程中,你发现了 ABCD的
对边AD与CB,AB与CD之间具有怎样的数量关系?
对角∠BAD与∠DCB,∠ABC与∠CDA之间具有怎样的数量关系?
线段OA与OC,OB与OD之间具有怎样的数量关系
AB=CD,AD=BC
∠BAD=∠BCD,
∠ABC=∠ADC
A
D
C
B
O
OA=OC,OB=OD
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.
(2)∠BAD=∠DCB,∠ABC=∠CDA.
A
B
C
D
证明:如图所示,连接BD,在△ABD和△CDB中,
∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,即∠ABC=∠CDA.
归纳
1.平行四边形是中心对称图形,
它的对称中心是两条对角线的交点.
2.平行四边形性质定理:
平行四边形的对边相等,对角相等.
符号语言:
∵四边形ABCD是平行四边形,
∴AD=CB,AB=CD,∠A=∠C,∠B=∠D
A
D
C
B
O
已知:如图所示, ABCD的周长为22 已知:如图所示, ABCD的
周长为22 cm,△ABD的周长为18 cm,求对角线BD的长.
cm,△ABD的周长为18 cm,求对角线BD的长.
A
D
C
B
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC.
由已知条件,得2(AB+AD)=22,
∴AB+AD=11.
又∵AB+AD+BD=18,
∴BD=18-11=7.
做一做
例题示范
已知:如图所示,在 ABCD中,∠B+∠D=260°,∠A,∠C的度数.
A
D
C
B
解:在 ABCD中,
∵∠B=∠D,∠B+∠D=260°,∴∠B=∠D= =130°.
又∵AD∥CB,
∴∠A===50°.
∴∠C=∠A=50°.
随堂练习
2. 如图, ABCD中,EF∥BC,则图中平行四边形一共有_____个.
1. 在 ABCD中,若∠A=2∠B,则∠D的度数是_____.
3
60°
3. 已知 ABCD的周长为12,若AB=2BC,则CD的长为_____.
4. 如图, ABCD中,CE⊥AB与点E,若∠D=65°,则∠1=_____.
4
25°
1. 如图, ABCD周长为20,AB=4,BE平分∠ABC,则DE=_____.
2. 在 ABCD中,∠B的平分线把AD边长分成长度是5和7的两部分,则平行四边形的周长是=_______.
拓展提升
2
34或38
3. 如图, AOCB中,点A,C的坐标为A(1,1),C(2,0),则点B的坐标为________.
(3)
4. 如图,在等腰三角形ABC中,∠A=120°,顶点B在 ODEF的边DE上,已知∠1=40°,则∠2=______.
110°
归纳小结
平行四边形
两组对边分别平行的四边形
定义
性质1
平行四边形是中心对称图形,它的对称中心是两条对角线的交点
平行四边形的对边相等,对角相等
22.1 平行四边形的性质
第1课时
第二十二章 四边形
学习目标
1、理解平行四边形的概念;
2、探索并证明平行四边形的性质定理1.
学习重难点
探索并证明平行四边形的性质定理1.
探索并证明平行四边形的性质定理1.
难点
重点
创设情境
在我们的周围存在着许多的四边形. 观察下列图片,从中找出四边形,并就它们的共同特性和不同特性,和大家交流一下你的看法
新知引入
知识点1 平行四边形的表示方法
上面图片中的四边形可以归类为以下四种:
定义:两组对边分别平行的四边形叫做平行四边形.连接平行四边形不相邻的两个顶点的线段叫做平行四边形的对角线.两条对角线的交点叫做平行四边形的中心.
如图,四边形ABCD是平行四边形,记作“ ABCD”,读作“平行四边形ABCD”.线段AC,BD为 ABCD的两条对角线,点O为它的中心.
A
D
C
B
O
知识点2 平行四边形的性质
在半透明的纸上画一个 ABCD,再复制一个,将两个图形完全重合,用大头针钉在中心处,使下面的图形不动,将上面的图形绕中心O旋转180°,这两个图形能完全重合吗 平行四边形是不是中心对称图形 如果是中心对称图形,哪个点是它的对称中心 被对角线分成的三角形中,关于点O成中心对称的图形有几对
A
D
C
B
O
A
D
C
B
O
(C)
(B)
(A)
(D)
一起探究
2. 在上面的活动过程中,你发现了 ABCD的
对边AD与CB,AB与CD之间具有怎样的数量关系?
对角∠BAD与∠DCB,∠ABC与∠CDA之间具有怎样的数量关系?
线段OA与OC,OB与OD之间具有怎样的数量关系
AB=CD,AD=BC
∠BAD=∠BCD,
∠ABC=∠ADC
A
D
C
B
O
OA=OC,OB=OD
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.
(2)∠BAD=∠DCB,∠ABC=∠CDA.
A
B
C
D
证明:如图所示,连接BD,在△ABD和△CDB中,
∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,即∠ABC=∠CDA.
归纳
1.平行四边形是中心对称图形,
它的对称中心是两条对角线的交点.
2.平行四边形性质定理:
平行四边形的对边相等,对角相等.
符号语言:
∵四边形ABCD是平行四边形,
∴AD=CB,AB=CD,∠A=∠C,∠B=∠D
A
D
C
B
O
已知:如图所示, ABCD的周长为22 已知:如图所示, ABCD的
周长为22 cm,△ABD的周长为18 cm,求对角线BD的长.
cm,△ABD的周长为18 cm,求对角线BD的长.
A
D
C
B
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC.
由已知条件,得2(AB+AD)=22,
∴AB+AD=11.
又∵AB+AD+BD=18,
∴BD=18-11=7.
做一做
例题示范
已知:如图所示,在 ABCD中,∠B+∠D=260°,∠A,∠C的度数.
A
D
C
B
解:在 ABCD中,
∵∠B=∠D,∠B+∠D=260°,∴∠B=∠D= =130°.
又∵AD∥CB,
∴∠A===50°.
∴∠C=∠A=50°.
随堂练习
2. 如图, ABCD中,EF∥BC,则图中平行四边形一共有_____个.
1. 在 ABCD中,若∠A=2∠B,则∠D的度数是_____.
3
60°
3. 已知 ABCD的周长为12,若AB=2BC,则CD的长为_____.
4. 如图, ABCD中,CE⊥AB与点E,若∠D=65°,则∠1=_____.
4
25°
1. 如图, ABCD周长为20,AB=4,BE平分∠ABC,则DE=_____.
2. 在 ABCD中,∠B的平分线把AD边长分成长度是5和7的两部分,则平行四边形的周长是=_______.
拓展提升
2
34或38
3. 如图, AOCB中,点A,C的坐标为A(1,1),C(2,0),则点B的坐标为________.
(3)
4. 如图,在等腰三角形ABC中,∠A=120°,顶点B在 ODEF的边DE上,已知∠1=40°,则∠2=______.
110°
归纳小结
平行四边形
两组对边分别平行的四边形
定义
性质1
平行四边形是中心对称图形,它的对称中心是两条对角线的交点
平行四边形的对边相等,对角相等
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
