6.3 二元一次方程组的应用 第1课时 课件 (共23张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 6.3 二元一次方程组的应用 第1课时 课件 (共23张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 953.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第六章 二元一次方程组
6. 3 二元一次方程组的应用
第1课时
学习目标
1.会类比一元一次方程的应用用二元一次方程组找实际问题中的等量关系;
2.掌握解二元一次方程应用题步骤;
3.感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识.
学习重难点
掌握解二元一次方程应用题步骤.
感受二元一次方程组的广泛应用,增强数学的应用意识.
难点
重点
回顾复习
用代入消元法解二元一次方程组的步骤:
变形
选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数.
把 y=ax+b (或 x=ay+b) 代入另一个没有变形的方程.
代入
求解
写解
把两个未知数的值用大括号联立起来.
解消元后的一元一次方程.
把求得的未知数的值代入步骤1中变形后的方程.
回代
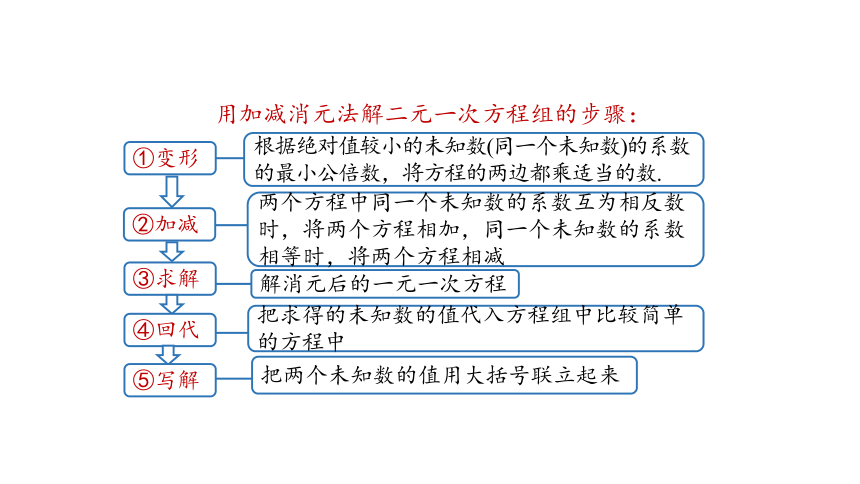
用加减消元法解二元一次方程组的步骤:
根据绝对值较小的未知数(同一个未知数)的系数的最小公倍数,将方程的两边都乘适当的数.
①变形
两个方程中同一个未知数的系数互为相反数时,将两个方程相加,同一个未知数的系数相等时,将两个方程相减
②加减
解消元后的一元一次方程
③求解
把求得的未知数的值代入方程组中比较简单的方程中
④回代
把两个未知数的值用大括号联立起来
⑤写解
情境导入
大马和小马驮着货物在途中有一段对话:
大马说:“把我驮着的东西给你1包多好啊,
这样咱俩驮的东西就一样多了。”
小马说:“我还想给你1包呢!”
大马说:“那可不行!如果你给我1包,我驮
的包数就是你的2倍了。”
请利用一元一次方程求出大马和小马各自所驮货物的包数。
1、大马的两句话,说出了哪两个等量关系?
大马驮物包数-1=小马驮物包数+1
大马驮物包数+1=(小马驮物包数-1)×2
一起探究
3、请你试着解出题中所列方程组,并与同学们进行交流。
例题示范
化肥厂往某地区发运了两批化肥,第一批装满了9节火车车厢和25辆卡车,共运走640t;第二批装满了12节火车车厢和10辆卡车,共运走了760t;平均每节火车车厢和每辆卡车分别装运化肥多少吨?
小组讨论:本题中的等量关系是:
第一批,9节火车车厢运货吨数+25辆卡车运货吨数=640
第二批,12节火车车厢运货吨数+10辆卡车运货吨数=760
例1
列二元一次
方程组解应用题的一般步骤
审:认真审题,明确等量关系
设:恰当地设未知数
列:依据等量关系列出方程组
验:检验是否符合题意和实际意义
答:写出答
解:解方程组,求出未知数的值
找等量关系的方法
1.抓住题目中的关键词,常见的关键词有:“比”“是”
“等于”等;
2.根据常见的数量关系,如体积公式、面积公式等,找等量关系;
3.挖掘题目中的隐含条件,如飞机沿同一航线航行,顺风航行与逆风航行的路程相等;
4.借助列表格、画线段示意图等方法找等量关系.
某车间有工人660名,生产甲、乙两种零件,已知每人每天平均生产甲种零件14个或乙种零件20个,1个甲种零件与2个乙种零件为一套.如何调配人员可使每天生产的两种零件刚好配套?
分析本题中等量关系:
生产甲种零件的人数+生产乙种零件的人数=660
甲种零件的个数×2=乙种零件的个数
例2
随堂练习
1.(中考·深圳)某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满.设大房间有x个,小房间有y个,下列方程组正确的是( )
A. B.
C. D.
A
x+y=70
8x+6y=480
x+y=480
6x+8y=70
x+y=480
8x+6y=70
x+y=70
6x+8y=480
2.(中考 梧州)运用方程或方程组解决实际问题:
若干学生分若干支铅笔,如果每人5支,那么多余3支;如果每人7支,那么缺5支.试问有多少名学生?共有多少支铅笔?
解:设共有x名学生,y支铅笔,
依题意得 解得,
答:共有4名学生,23支铅笔.
3.一支部队第一天行军 4 h,第二天行军 5 h,两天共行军 98 km,且第一天比第二天少走 2 km,第一天和第二天行军的平均速度各是多少?
解:设第一天行军的平均速度为 x km/h,第二天行军的平均速度为 y km/h.
①+②,得 8x=96,解得 x=12,把 x=12代入①,得 48+5y=98.
解得 y=10.∴这个方程组的解为
答:第一天行军的平均速度为 12 km/h,第二天行军的平均速度为 10 km/h.
由题意,
拓展提升
B
1.无人知甲、乙两人年龄,只知道当甲是乙现在的年龄时, 乙只有2岁; 当乙到甲现在的年龄时,甲是38岁了,问甲、乙现在的年龄各是( )
A.24岁,14岁
B.26岁,14岁
C.26岁,16岁
D.28岁,16岁
2.(中考 大连)某校为实现垃圾分类投放,准备在校园内摆放大、小两种垃圾桶.购买2个大垃圾桶和4个小垃圾桶共需600元;购买6个大垃圾桶和8个小垃圾桶共需1 560元.
(1)求大、小两种垃圾桶的单价;
(2)该校购买8个大垃圾桶和24个小垃圾桶共需多少元?
解:(1)设大垃圾桶的单价为x元,小垃圾桶的单价
为y元,
依题意,得 解得
答:大垃圾桶的单价为180元,小垃圾桶的单价为60元.
(2)180×8+60×24=2 880(元).
答:该校购买8个大垃圾桶和24个小垃圾桶共需2 880元.
3.某家商店的帐目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
解:有误,理由:设一支牙刷的价格为x元,一盒牙膏的价格为y元.由题意,得
即
方程组无解.∴这个记录有误.
归纳小结
列二元一次
方程组解应用题的一般步骤
审:认真审题,明确等量关系
设:恰当地设未知数
列:依据等量关系列出方程组
验:检验是否符合题意和实际意义
答:写出答
解:解方程组,求出未知数的值
第六章 二元一次方程组
6. 3 二元一次方程组的应用
第1课时
学习目标
1.会类比一元一次方程的应用用二元一次方程组找实际问题中的等量关系;
2.掌握解二元一次方程应用题步骤;
3.感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识.
学习重难点
掌握解二元一次方程应用题步骤.
感受二元一次方程组的广泛应用,增强数学的应用意识.
难点
重点
回顾复习
用代入消元法解二元一次方程组的步骤:
变形
选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数.
把 y=ax+b (或 x=ay+b) 代入另一个没有变形的方程.
代入
求解
写解
把两个未知数的值用大括号联立起来.
解消元后的一元一次方程.
把求得的未知数的值代入步骤1中变形后的方程.
回代
用加减消元法解二元一次方程组的步骤:
根据绝对值较小的未知数(同一个未知数)的系数的最小公倍数,将方程的两边都乘适当的数.
①变形
两个方程中同一个未知数的系数互为相反数时,将两个方程相加,同一个未知数的系数相等时,将两个方程相减
②加减
解消元后的一元一次方程
③求解
把求得的未知数的值代入方程组中比较简单的方程中
④回代
把两个未知数的值用大括号联立起来
⑤写解
情境导入
大马和小马驮着货物在途中有一段对话:
大马说:“把我驮着的东西给你1包多好啊,
这样咱俩驮的东西就一样多了。”
小马说:“我还想给你1包呢!”
大马说:“那可不行!如果你给我1包,我驮
的包数就是你的2倍了。”
请利用一元一次方程求出大马和小马各自所驮货物的包数。
1、大马的两句话,说出了哪两个等量关系?
大马驮物包数-1=小马驮物包数+1
大马驮物包数+1=(小马驮物包数-1)×2
一起探究
3、请你试着解出题中所列方程组,并与同学们进行交流。
例题示范
化肥厂往某地区发运了两批化肥,第一批装满了9节火车车厢和25辆卡车,共运走640t;第二批装满了12节火车车厢和10辆卡车,共运走了760t;平均每节火车车厢和每辆卡车分别装运化肥多少吨?
小组讨论:本题中的等量关系是:
第一批,9节火车车厢运货吨数+25辆卡车运货吨数=640
第二批,12节火车车厢运货吨数+10辆卡车运货吨数=760
例1
列二元一次
方程组解应用题的一般步骤
审:认真审题,明确等量关系
设:恰当地设未知数
列:依据等量关系列出方程组
验:检验是否符合题意和实际意义
答:写出答
解:解方程组,求出未知数的值
找等量关系的方法
1.抓住题目中的关键词,常见的关键词有:“比”“是”
“等于”等;
2.根据常见的数量关系,如体积公式、面积公式等,找等量关系;
3.挖掘题目中的隐含条件,如飞机沿同一航线航行,顺风航行与逆风航行的路程相等;
4.借助列表格、画线段示意图等方法找等量关系.
某车间有工人660名,生产甲、乙两种零件,已知每人每天平均生产甲种零件14个或乙种零件20个,1个甲种零件与2个乙种零件为一套.如何调配人员可使每天生产的两种零件刚好配套?
分析本题中等量关系:
生产甲种零件的人数+生产乙种零件的人数=660
甲种零件的个数×2=乙种零件的个数
例2
随堂练习
1.(中考·深圳)某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满.设大房间有x个,小房间有y个,下列方程组正确的是( )
A. B.
C. D.
A
x+y=70
8x+6y=480
x+y=480
6x+8y=70
x+y=480
8x+6y=70
x+y=70
6x+8y=480
2.(中考 梧州)运用方程或方程组解决实际问题:
若干学生分若干支铅笔,如果每人5支,那么多余3支;如果每人7支,那么缺5支.试问有多少名学生?共有多少支铅笔?
解:设共有x名学生,y支铅笔,
依题意得 解得,
答:共有4名学生,23支铅笔.
3.一支部队第一天行军 4 h,第二天行军 5 h,两天共行军 98 km,且第一天比第二天少走 2 km,第一天和第二天行军的平均速度各是多少?
解:设第一天行军的平均速度为 x km/h,第二天行军的平均速度为 y km/h.
①+②,得 8x=96,解得 x=12,把 x=12代入①,得 48+5y=98.
解得 y=10.∴这个方程组的解为
答:第一天行军的平均速度为 12 km/h,第二天行军的平均速度为 10 km/h.
由题意,
拓展提升
B
1.无人知甲、乙两人年龄,只知道当甲是乙现在的年龄时, 乙只有2岁; 当乙到甲现在的年龄时,甲是38岁了,问甲、乙现在的年龄各是( )
A.24岁,14岁
B.26岁,14岁
C.26岁,16岁
D.28岁,16岁
2.(中考 大连)某校为实现垃圾分类投放,准备在校园内摆放大、小两种垃圾桶.购买2个大垃圾桶和4个小垃圾桶共需600元;购买6个大垃圾桶和8个小垃圾桶共需1 560元.
(1)求大、小两种垃圾桶的单价;
(2)该校购买8个大垃圾桶和24个小垃圾桶共需多少元?
解:(1)设大垃圾桶的单价为x元,小垃圾桶的单价
为y元,
依题意,得 解得
答:大垃圾桶的单价为180元,小垃圾桶的单价为60元.
(2)180×8+60×24=2 880(元).
答:该校购买8个大垃圾桶和24个小垃圾桶共需2 880元.
3.某家商店的帐目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
解:有误,理由:设一支牙刷的价格为x元,一盒牙膏的价格为y元.由题意,得
即
方程组无解.∴这个记录有误.
归纳小结
列二元一次
方程组解应用题的一般步骤
审:认真审题,明确等量关系
设:恰当地设未知数
列:依据等量关系列出方程组
验:检验是否符合题意和实际意义
答:写出答
解:解方程组,求出未知数的值
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
