7.1 命题 第2课时 课件 (共18张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 7.1 命题 第2课时 课件 (共18张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 725.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 21:27:39 | ||
图片预览





文档简介
(共18张PPT)
第七章 相交线与平行线
7.1 命题
第2课时
学习目标
1.理解和掌握说理、基本事实、定理及演绎推理的概念.
2.掌握说理的一般步骤.
学习重难点
理解和掌握说理、基本事实、定理及演绎推理的概念.
掌握说理的一般步骤.
难点
重点
问题导入
如何证实一个命题是真命题呢?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的
能不能根据已经知道的真命题证实呢
哦……那可
怎么办
新知引入
知识点1 说理与基本事实
观察与思考
问题1 在图1中,AB和CD是直线吗?请你先观察,后判断,然后利用直尺验证你的结论是否正确.
图1
A
B
C
D
AB是直线;
CD是直线.
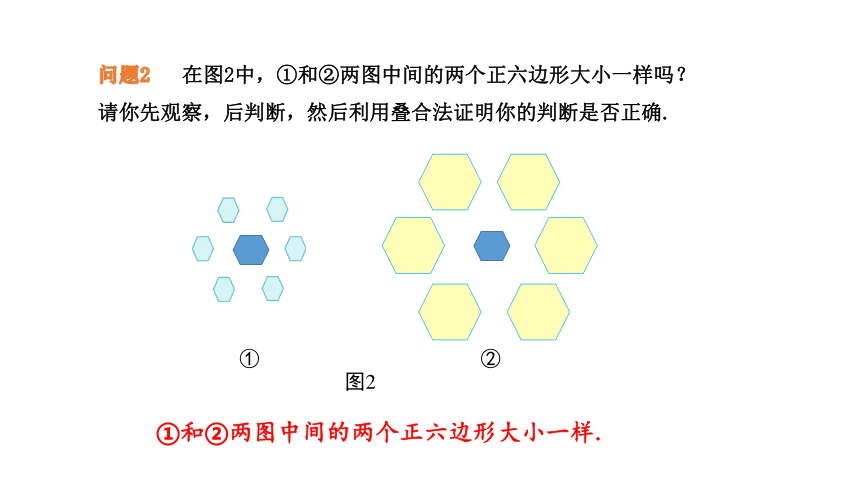
问题2 在图2中,①和②两图中间的两个正六边形大小一样吗? 请你先观察,后判断,然后利用叠合法证明你的判断是否正确.
图2
①
②
①和②两图中间的两个正六边形大小一样.
问题3 如果a=-b,那么a2=b2.由此得出:当a=-b时,a3=b3.你认为后一个命题正确吗?为什么?
解:后一个命题不正确.
说明:设a=1,b=-1,则a=-b.(符合命题的条件)
因为a3=13=1,b3=(-1)3=-1,
则a3≠b3.(不符合命题的结论)
所以命题“当a=-b时,a3=b3”是个假命题.
总结归纳
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
有些命题经过实践经验被公认为真命题,我们把这样的命题叫做基本事实.
我们学习过的基本事实有哪些呢?
1.过平面上两点,有且只有一条直线,简记为“两点确定一条直线”。
2.两点之间的连线中,线段最短。
简记为“两点之间线段最短”。
3.等式的性质
知识点2 定理与演绎推理
互动探究
观察相邻两个奇数的和:
1
3
5
7
9
···
4
8
12
16
···
问题1 相邻两个奇数的和与4之间有什么关系?请提出你的猜想.
相邻两个奇数的和都能被4的整除.
实验、归纳是常用的发现命题的方法.
问题2 通过说理,验证你的猜想正确与否.
说明:设相邻两奇数为2k-1,2k+1,其中k是整数.
(符合命题的条件)
因为(2k-1)+(2k+1)=4k.(符合命题的结论)
所以“相邻两个奇数的和能被4整除”这个命题是真命题.
例题示范
例 如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD(等量加等量,和相等或等式的性质),
所以 AD=CB(线段和的定义).
知识要点
依据已有的事实(包括定义、基本事实、已被确认的真命题),按照确定的规则,得到某个具体的结论的推理就是演绎推理.
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
随堂练习
1.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到了三角形有三个角
C.老师告诉了我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
2.下列说法中不正确的是( )
A.证实命题正确与否的推理过程就是说理
B.命题是判断一件事的语句
C.基本事实的正确与否必须通过推理的方法来证实
D.定理都是真命题,但真命题不一定是定理
C
3.关于说理,下列说法不正确的是( )
A.说理是说明命题是真命题的过程
B.要说明一个命题是真命题常常通过推理的方式
C.要说明一个命题是假命题常采用举反例的方式
D.真命题与假命题都可以通过举反例来说明
D
拓展提升
可以作为说理的依据的是( )
A.已知条件
B.基本事实
C.定理
D.以上三种都对
D
1
2
阅读下面命题及说理过程,在括号内填上推理的依据.
命题:如图所示,直线AB,CD
相交于点O,那么∠1=∠2.
理由:因为∠1+∠AOD=180°( ),
∠2+∠AOD=180°( ),
所以∠1+∠AOD=∠2+∠AOD ( ),
所以∠1=∠2( ).
平角定义
平角定义
等量代换
等式的基本性质
如图,P 是线段AB 的中点,M 为PB上任意一点,探究2PM与AM-BM之间的大小关系,并说明理由.
3
2PM=AM-BM.理由:因为P 是线段AB 的中点,
所以AP=BP.
所以AM-BM=AP+PM-(BP-PM)=AP+PM-(AP-PM)=2PM.
解:
归纳小结
真命题
说理的依据
基本事实
定理
定义
说理的过程
演绎推理
第七章 相交线与平行线
7.1 命题
第2课时
学习目标
1.理解和掌握说理、基本事实、定理及演绎推理的概念.
2.掌握说理的一般步骤.
学习重难点
理解和掌握说理、基本事实、定理及演绎推理的概念.
掌握说理的一般步骤.
难点
重点
问题导入
如何证实一个命题是真命题呢?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的
能不能根据已经知道的真命题证实呢
哦……那可
怎么办
新知引入
知识点1 说理与基本事实
观察与思考
问题1 在图1中,AB和CD是直线吗?请你先观察,后判断,然后利用直尺验证你的结论是否正确.
图1
A
B
C
D
AB是直线;
CD是直线.
问题2 在图2中,①和②两图中间的两个正六边形大小一样吗? 请你先观察,后判断,然后利用叠合法证明你的判断是否正确.
图2
①
②
①和②两图中间的两个正六边形大小一样.
问题3 如果a=-b,那么a2=b2.由此得出:当a=-b时,a3=b3.你认为后一个命题正确吗?为什么?
解:后一个命题不正确.
说明:设a=1,b=-1,则a=-b.(符合命题的条件)
因为a3=13=1,b3=(-1)3=-1,
则a3≠b3.(不符合命题的结论)
所以命题“当a=-b时,a3=b3”是个假命题.
总结归纳
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
有些命题经过实践经验被公认为真命题,我们把这样的命题叫做基本事实.
我们学习过的基本事实有哪些呢?
1.过平面上两点,有且只有一条直线,简记为“两点确定一条直线”。
2.两点之间的连线中,线段最短。
简记为“两点之间线段最短”。
3.等式的性质
知识点2 定理与演绎推理
互动探究
观察相邻两个奇数的和:
1
3
5
7
9
···
4
8
12
16
···
问题1 相邻两个奇数的和与4之间有什么关系?请提出你的猜想.
相邻两个奇数的和都能被4的整除.
实验、归纳是常用的发现命题的方法.
问题2 通过说理,验证你的猜想正确与否.
说明:设相邻两奇数为2k-1,2k+1,其中k是整数.
(符合命题的条件)
因为(2k-1)+(2k+1)=4k.(符合命题的结论)
所以“相邻两个奇数的和能被4整除”这个命题是真命题.
例题示范
例 如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD(等量加等量,和相等或等式的性质),
所以 AD=CB(线段和的定义).
知识要点
依据已有的事实(包括定义、基本事实、已被确认的真命题),按照确定的规则,得到某个具体的结论的推理就是演绎推理.
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
随堂练习
1.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到了三角形有三个角
C.老师告诉了我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
2.下列说法中不正确的是( )
A.证实命题正确与否的推理过程就是说理
B.命题是判断一件事的语句
C.基本事实的正确与否必须通过推理的方法来证实
D.定理都是真命题,但真命题不一定是定理
C
3.关于说理,下列说法不正确的是( )
A.说理是说明命题是真命题的过程
B.要说明一个命题是真命题常常通过推理的方式
C.要说明一个命题是假命题常采用举反例的方式
D.真命题与假命题都可以通过举反例来说明
D
拓展提升
可以作为说理的依据的是( )
A.已知条件
B.基本事实
C.定理
D.以上三种都对
D
1
2
阅读下面命题及说理过程,在括号内填上推理的依据.
命题:如图所示,直线AB,CD
相交于点O,那么∠1=∠2.
理由:因为∠1+∠AOD=180°( ),
∠2+∠AOD=180°( ),
所以∠1+∠AOD=∠2+∠AOD ( ),
所以∠1=∠2( ).
平角定义
平角定义
等量代换
等式的基本性质
如图,P 是线段AB 的中点,M 为PB上任意一点,探究2PM与AM-BM之间的大小关系,并说明理由.
3
2PM=AM-BM.理由:因为P 是线段AB 的中点,
所以AP=BP.
所以AM-BM=AP+PM-(BP-PM)=AP+PM-(AP-PM)=2PM.
解:
归纳小结
真命题
说理的依据
基本事实
定理
定义
说理的过程
演绎推理
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
