7.2 相交线 第2课时 课件 (共36张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 7.2 相交线 第2课时 课件 (共36张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 21:30:47 | ||
图片预览











文档简介
(共36张PPT)
第七章 相交线与平行线
7. 2 相交线
第2课时
学习目标
1.理解垂线、垂线段的概念,能过一点画已知直线的垂线,掌握垂线的基本事实.
2.通过探究掌握“垂线段最短”这一性质.
学习重难点
理解垂线、垂线段的概念,掌握垂线的基本事实.掌握“垂线段最短”这一性质.
理解垂线、垂线段的概念,掌握垂线的基本事实.掌握“垂线段最短”这一性质.
难点
重点
创设情境
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
新知引入
知识点1 垂线
1.垂直的定义:在相交线的模型中,固定木条a,转动木条b.当b的位置发生变化时,a、b所成的∠ 也会发生变化.当∠ = 90°时,我们说a与b互相垂直,记作a⊥b.
垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.在下图中,AB⊥CD,垂足为O.
A
B
C
D
O
A
B
C
D
O
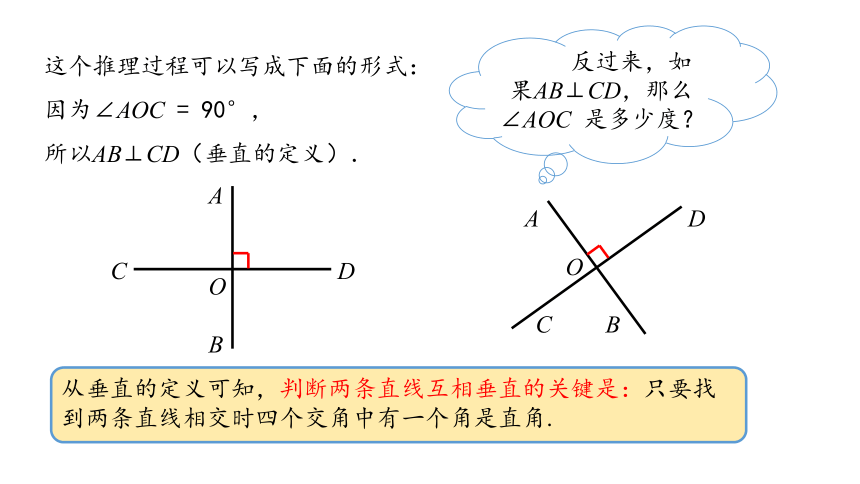
这个推理过程可以写成下面的形式:
因为∠AOC = 90°,
所以AB⊥CD(垂直的定义).
反过来,如果AB⊥CD,那么∠AOC 是多少度?
A
B
C
D
O
A
B
C
D
O
从垂直的定义可知,判断两条直线互相垂直的关键是:只要找到两条直线相交时四个交角中有一个角是直角.
日常生活中,两条直线互相垂直的情形很常见,说出下图中的一些互相垂直的直线.你能再举出其他例子吗
窗户的四边
围栏
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
垂直的表示方法:
如果用 l,m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
垂直的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =
∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
A
B
C
D
O
例题示范
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
例2 如图,直线AB,CD相交于点O,过O点画射线OE,OF,使OE⊥CD,OD平分∠BOF.如果∠BOE=50°,求∠AOC,∠EOF和∠AOF的度数.
解:因为OE⊥CD,所以∠DOE=90°(垂直的定义).
因为∠BOE=50°,所以∠AOC=∠BOD=
∠DOE-∠BOE=90°-50°=40°.
因为OD平分∠BOF,所以∠BOF=2∠BOD=80°.
所以∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
知识点2 垂线的画法及基本事实
新知引入
1.落.
2.画.
如图,已知直线 l,作 l 的垂线.
l
O
A
这样画直线 l 的垂线可以画几条?
无数条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 如果作线段互相垂直或作射线的垂
线,实际上是作线段所在的直线互相垂直,或作射线
所在的直线的垂线,因为射线和线段都是直线的一部
分.在垂线的画法中,有时需延长线段,垂足在延长
线上,并记上直角符号“﹁”.
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
基本事实:经过直线上或直线外的一点,有且只有一条直线与已知直线垂直.
总结归纳
例题示范
例 如图,分别过点 P 作线段 MN 的垂线.
M
N
P
M
N
P
Q
P
M
N
Q
P
M
N
Q
知识点3 垂线段的定义及性质
新知引入
猜一猜:哪条线段是垂线段?
C
D
E
l
B
A
定义:过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
想一想:比较AB,AC,AD,AE 的长短,这些线段中,哪一条最短?
C
D
E
l
B
A
线段AD最短.
想一想:以点A为圆心,AD的长为半径画弧,圆弧分别与线段AB,AC,AE相交于点B1,C1,E1.线段AB1,AC1,AE1,AD相等吗?由此能进一步验证你的猜想吗?
C
D
E
l
B
A
B1
C1
E1
垂线性质:直线外一点与直线上各点连接的所有线段中,垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
总结归纳
注意:
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
例题示范
例 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
∟
理由:垂线段最短
N
随堂练习
1.如图所示,直线 AB ⊥ CD 于点 O ,直线 EF经过点 O ,若∠1 = 26°,则∠2 的度数是( )
A. 26°
B. 64°
C. 54°
D. 以上答案都不对
B
2.如图,点 A,B,C 在直线 l 上,PB⊥l,PA = 6 cm,PB = 5 cm,PC = 7 cm,则点 P 到直线 l 的距离是 cm.
5
3.如图,AB ⊥ l ,BC ⊥ l ,B 为垂足,那么A、B、C 三点在同一直线上吗?为什么?
解:A、B、C 三点在同一直线上.
因为AB ⊥ l ,BC ⊥ l . 且交点都为 B .
所以A、B、C 三点在同一直线上(在同一平面内,过一点有且只有一条直线与已知直线垂直).
4.如图,AO⊥FD,OD 为∠BOC 的平分线,OE 为射线OB 的反向延长线,若∠AOB = 40°,求∠EOF、∠COE 的度数.
解:因为AO⊥OD且∠AOB=40°,
所以∠BOD=90°-40°=50°,所以∠EOF=50°.
又因为OD平分∠BOC,所以∠DOC=∠BOD=50°,
所以∠COE=180°-50°-50°=80°.
A
F
D
O
B
C
E
5.如图,平原上有A,B,C,D 四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池 H 中,怎样开渠最短并说明根据.
解:(1)如图,连接AD,BC 交于 H ,因为两点之间线段最短,所以 H 为蓄水池位置,它到四个村庄距离之和最小.
H
(2)如图,过 H 作 HG⊥EF ,垂足为 G .“过直线外一点与直线各点的连线中,垂线段最短”是把河水引入蓄水池 H 中开渠最短的根据.
G
H
1.点 P 为直线 l 外一点,点 A,B,C 为直线 l 上三点,PA = 2 cm,PB = 3 cm,PC = 4 cm,则点 P 到直线 l 的距离( )
A.等于 2 cm
B.小于 2 cm
C.大于 2cm
D.不大于 2 cm
D
拓展提升
2.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段 CD 的长度是点 C 到 AB 的距离;
②线段 AC 是点 A 到 BC 的距离;
③ AB > AC > CD;
④线段 BC 是点 B 到 AC 的距离;
⑤ CD < BC < AB.
A.2个 B.3个 C.4个 D.5个
B
3.如图,直线 AB,CD 相交于 O 点,OM⊥AB 于 O .
(1)若∠1 =∠2,求∠NOD;
(2)若∠BOC = 4∠1,求∠AOC 与∠MOD.
解:(1)因为 OM ⊥ AB ,所以∠1 + ∠AOC = 90°.
又∠1 = ∠2,所以∠2 + ∠AOC = 90°,
所以∠NOD = 180°-(∠2 + ∠AOC)= 180°- 90°= 90°.
(2)由已知条件∠BOC =4∠1,即 90°+∠1 = 4∠1,
可得∠1 = 30°,所以∠AOC = 90°- 30° = 60°,
所以由对顶角相等可得∠BOD = 60°,
所以∠MOD = 90°+∠BOD = 150°.
4.如图,火车站、码头分别位于 A,B 两点,直线 a 和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
A
a
B
b
两点之间,线段最短
垂线段最短
垂线段最短
归纳小结
垂线
垂线和垂线段
定义
基本事实
垂线段
定义
点到直线的距离
经过直线上或直线外的一点,有且只有一条直线与已知直线垂直.
垂线段最短
性质
第七章 相交线与平行线
7. 2 相交线
第2课时
学习目标
1.理解垂线、垂线段的概念,能过一点画已知直线的垂线,掌握垂线的基本事实.
2.通过探究掌握“垂线段最短”这一性质.
学习重难点
理解垂线、垂线段的概念,掌握垂线的基本事实.掌握“垂线段最短”这一性质.
理解垂线、垂线段的概念,掌握垂线的基本事实.掌握“垂线段最短”这一性质.
难点
重点
创设情境
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
新知引入
知识点1 垂线
1.垂直的定义:在相交线的模型中,固定木条a,转动木条b.当b的位置发生变化时,a、b所成的∠ 也会发生变化.当∠ = 90°时,我们说a与b互相垂直,记作a⊥b.
垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.在下图中,AB⊥CD,垂足为O.
A
B
C
D
O
A
B
C
D
O
这个推理过程可以写成下面的形式:
因为∠AOC = 90°,
所以AB⊥CD(垂直的定义).
反过来,如果AB⊥CD,那么∠AOC 是多少度?
A
B
C
D
O
A
B
C
D
O
从垂直的定义可知,判断两条直线互相垂直的关键是:只要找到两条直线相交时四个交角中有一个角是直角.
日常生活中,两条直线互相垂直的情形很常见,说出下图中的一些互相垂直的直线.你能再举出其他例子吗
窗户的四边
围栏
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
垂直的表示方法:
如果用 l,m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
垂直的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =
∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
A
B
C
D
O
例题示范
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
例2 如图,直线AB,CD相交于点O,过O点画射线OE,OF,使OE⊥CD,OD平分∠BOF.如果∠BOE=50°,求∠AOC,∠EOF和∠AOF的度数.
解:因为OE⊥CD,所以∠DOE=90°(垂直的定义).
因为∠BOE=50°,所以∠AOC=∠BOD=
∠DOE-∠BOE=90°-50°=40°.
因为OD平分∠BOF,所以∠BOF=2∠BOD=80°.
所以∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
知识点2 垂线的画法及基本事实
新知引入
1.落.
2.画.
如图,已知直线 l,作 l 的垂线.
l
O
A
这样画直线 l 的垂线可以画几条?
无数条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 如果作线段互相垂直或作射线的垂
线,实际上是作线段所在的直线互相垂直,或作射线
所在的直线的垂线,因为射线和线段都是直线的一部
分.在垂线的画法中,有时需延长线段,垂足在延长
线上,并记上直角符号“﹁”.
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
基本事实:经过直线上或直线外的一点,有且只有一条直线与已知直线垂直.
总结归纳
例题示范
例 如图,分别过点 P 作线段 MN 的垂线.
M
N
P
M
N
P
Q
P
M
N
Q
P
M
N
Q
知识点3 垂线段的定义及性质
新知引入
猜一猜:哪条线段是垂线段?
C
D
E
l
B
A
定义:过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
想一想:比较AB,AC,AD,AE 的长短,这些线段中,哪一条最短?
C
D
E
l
B
A
线段AD最短.
想一想:以点A为圆心,AD的长为半径画弧,圆弧分别与线段AB,AC,AE相交于点B1,C1,E1.线段AB1,AC1,AE1,AD相等吗?由此能进一步验证你的猜想吗?
C
D
E
l
B
A
B1
C1
E1
垂线性质:直线外一点与直线上各点连接的所有线段中,垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
总结归纳
注意:
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
例题示范
例 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
∟
理由:垂线段最短
N
随堂练习
1.如图所示,直线 AB ⊥ CD 于点 O ,直线 EF经过点 O ,若∠1 = 26°,则∠2 的度数是( )
A. 26°
B. 64°
C. 54°
D. 以上答案都不对
B
2.如图,点 A,B,C 在直线 l 上,PB⊥l,PA = 6 cm,PB = 5 cm,PC = 7 cm,则点 P 到直线 l 的距离是 cm.
5
3.如图,AB ⊥ l ,BC ⊥ l ,B 为垂足,那么A、B、C 三点在同一直线上吗?为什么?
解:A、B、C 三点在同一直线上.
因为AB ⊥ l ,BC ⊥ l . 且交点都为 B .
所以A、B、C 三点在同一直线上(在同一平面内,过一点有且只有一条直线与已知直线垂直).
4.如图,AO⊥FD,OD 为∠BOC 的平分线,OE 为射线OB 的反向延长线,若∠AOB = 40°,求∠EOF、∠COE 的度数.
解:因为AO⊥OD且∠AOB=40°,
所以∠BOD=90°-40°=50°,所以∠EOF=50°.
又因为OD平分∠BOC,所以∠DOC=∠BOD=50°,
所以∠COE=180°-50°-50°=80°.
A
F
D
O
B
C
E
5.如图,平原上有A,B,C,D 四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池 H 中,怎样开渠最短并说明根据.
解:(1)如图,连接AD,BC 交于 H ,因为两点之间线段最短,所以 H 为蓄水池位置,它到四个村庄距离之和最小.
H
(2)如图,过 H 作 HG⊥EF ,垂足为 G .“过直线外一点与直线各点的连线中,垂线段最短”是把河水引入蓄水池 H 中开渠最短的根据.
G
H
1.点 P 为直线 l 外一点,点 A,B,C 为直线 l 上三点,PA = 2 cm,PB = 3 cm,PC = 4 cm,则点 P 到直线 l 的距离( )
A.等于 2 cm
B.小于 2 cm
C.大于 2cm
D.不大于 2 cm
D
拓展提升
2.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段 CD 的长度是点 C 到 AB 的距离;
②线段 AC 是点 A 到 BC 的距离;
③ AB > AC > CD;
④线段 BC 是点 B 到 AC 的距离;
⑤ CD < BC < AB.
A.2个 B.3个 C.4个 D.5个
B
3.如图,直线 AB,CD 相交于 O 点,OM⊥AB 于 O .
(1)若∠1 =∠2,求∠NOD;
(2)若∠BOC = 4∠1,求∠AOC 与∠MOD.
解:(1)因为 OM ⊥ AB ,所以∠1 + ∠AOC = 90°.
又∠1 = ∠2,所以∠2 + ∠AOC = 90°,
所以∠NOD = 180°-(∠2 + ∠AOC)= 180°- 90°= 90°.
(2)由已知条件∠BOC =4∠1,即 90°+∠1 = 4∠1,
可得∠1 = 30°,所以∠AOC = 90°- 30° = 60°,
所以由对顶角相等可得∠BOD = 60°,
所以∠MOD = 90°+∠BOD = 150°.
4.如图,火车站、码头分别位于 A,B 两点,直线 a 和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
A
a
B
b
两点之间,线段最短
垂线段最短
垂线段最短
归纳小结
垂线
垂线和垂线段
定义
基本事实
垂线段
定义
点到直线的距离
经过直线上或直线外的一点,有且只有一条直线与已知直线垂直.
垂线段最短
性质
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
