7.6 图形的平移 课件 (共36张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 7.6 图形的平移 课件 (共36张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览








文档简介
(共36张PPT)
第七章 相交线与平行线
7. 6 图形的平移
学习目标
1.理解平移的概念及决定因素.
2.会找出平移前后图形中对应点、对应角和对应线段.
3.掌握平移的性质及其运用.
学习重难点
掌握平移的性质及其运用.
理解平移的概念及决定因素.
难点
重点
回顾复习
小学阶段我们学习了哪些图形的变换方法?
平移、轴对称和旋转.
创设情境
仔细观察下面一些美丽的图案,它们有什么共同的特点 能否根据其中的一部分绘制出整个图案?
新知引入
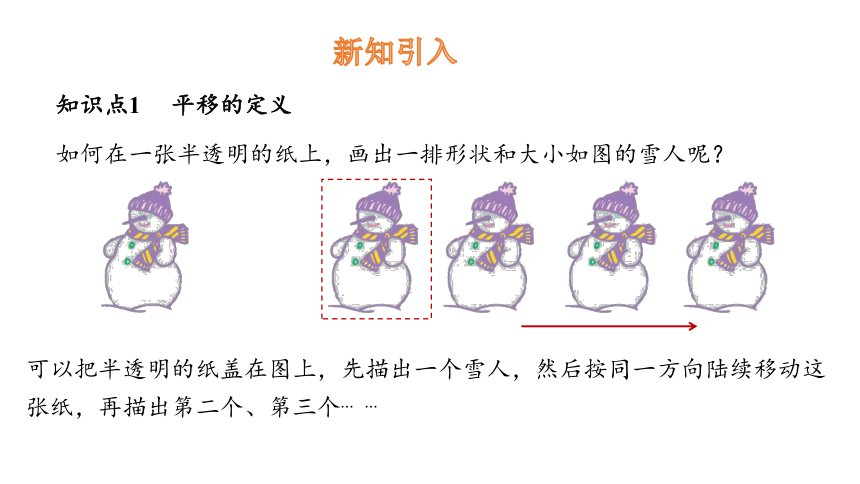
知识点1 平移的定义
如何在一张半透明的纸上,画出一排形状和大小如图的雪人呢?
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个
比较:画出的这些小雪人和已知的图片.
说一说:什么改变了?什么没改变?
1. 把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
归纳
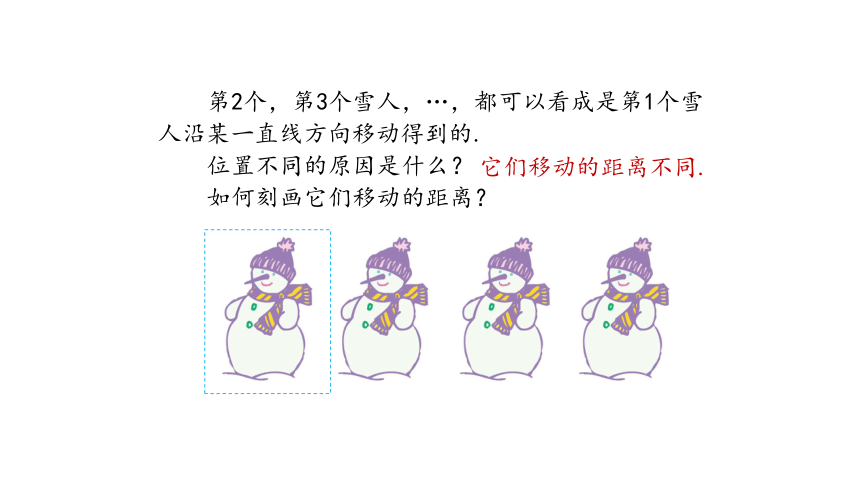
第2个,第3个雪人,…,都可以看成是第1个雪人沿某一直线方向移动得到的.
位置不同的原因是什么?
如何刻画它们移动的距离?
它们移动的距离不同.
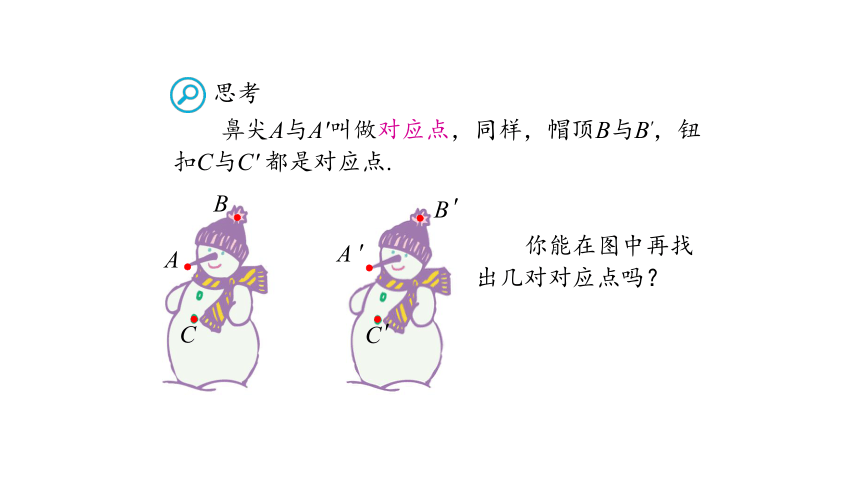
鼻尖A与A'叫做对应点,同样,帽顶B与B',钮扣C与C' 都是对应点.
你能在图中再找出几对对应点吗?
A
A
'
B
C
B
'
C
'
思考
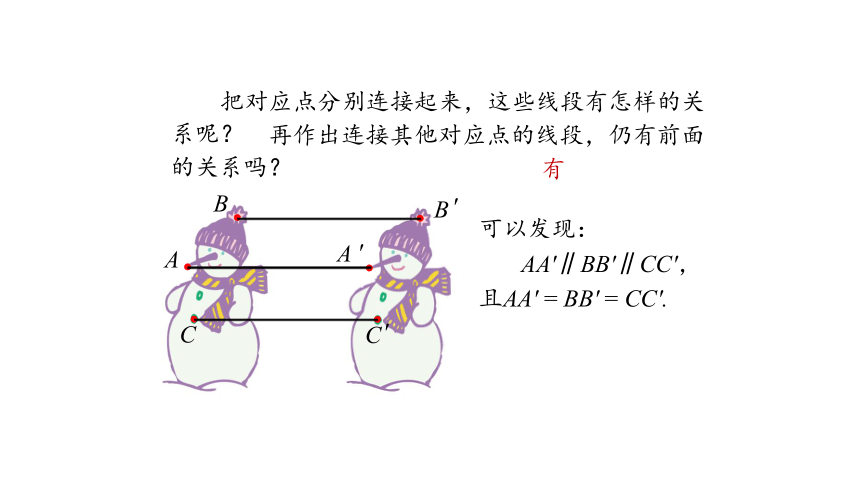
把对应点分别连接起来,这些线段有怎样的关系呢?
可以发现:
AA′∥BB′∥CC′,
且AA′ = BB′ = CC′.
再作出连接其他对应点的线段,仍有前面的关系吗?
A
A
'
B
C
B
'
C
'
有
2. 连接各组对应点的线段平行(或在同一条直线上)且相等.
归纳
图形的这种移动,叫做平移(translation).
A
A
'
B
C
B
'
C
'
观察以下几种移动,想一想平移有什么要素?
平移的要素:1. 平移的方向;2. 平移的距离.
注意:图形平移的方向可以是任意指定的方向,不限于是水平的或竖直的,但必须是直线方向.
图形的平移是整个图形都在移动,即图形中所有点、线平移的方向和平移的距离都相同,所以确定一个图形平移的方向和距离,只需确定图形上一个点平移的方向和距离即可.
例题示范
例1 将如图所示的图案平移后,可以得到的图案是( )
A
例2 下列现象:
(1)水平运输带上砖块的运动;
(2)高楼电梯上上下下迎接乘客;
(3)健身做呼啦圈运动;
(4)火车飞驰在一段平直的铁轨上;
(5)沸水中气泡的运动.
属于平移的是___________________.
(1)(2)(4)
新知引入
知识点2 平移的性质
如图,把三角形ABC 沿直线 PQ 平移,得到三角形DEF. 分析 AD、BE、CF 有怎样的数量关系和位置关系.
F
D
A
B
C
P
Q
E
AD//BE//CF, AD=BE=CF.
再画一些连接其他对应点的线段,你能得到什么结论?
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点. 连接各组对应点的线段平行(或在同一条直线上)且相等.
如图,把三角形ABC 沿直线 PQ 平移,得到三角形DEF. 分析对应线段间有怎样的数量关系和位置关系?对应角有什么关系?
F
D
A
B
C
P
Q
E
平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
注意:“连接各组对应点的线段”是原图形上的点与平移后的图形上的点连接而成的;而“对应线段”就存在于原来的图形与平移后的图形之中,是图形的一部分.
平移的性质
1. 平移后得到的新图形与原图形的形状、大小完全相同;
2. 连接各组对应点的线段平行(或在同一条直线上)且相等.
3. 平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
例题示范
例 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE之间有什么数量关系?
导引:
根据平移的特征可知:平移只改变图形的位置,不改变图形的大小;平移得到的图形与原来的图形是完全一样的,所以对应的线段之间是平行且相等的.
解: (1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
新知引入
知识点3 平移作图
如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
解:如图,连接AA' ,过点B作的平行线l,在l 上截取BB' =AA' ,则点B'就是点B的对应点.
类似地,作出点C的对应点 C' ,得到平移后的△A'B'C'.
B'
l
C'
1. 定:确定平移的方向和距离;
2. 找:找出确定图形形状的关键点;
3. 移:按平移的方向和距离平移各个关键点,
得到各个关键点的对应点;
4. 连:按原图形的顺序依次连接各对应点;
5. 写:写出结论.
平移作图的基本步骤
1. 平移的性质是平移作图的依据.
2. 确定一个图形平移后的位置需三个条件:
① 图形原来的位置;
② 平移的方向;
③ 平移的距离.
这三个条件缺一不可,只有这样,平移后的图形才唯一确定.
例题示范
例 如图所示,经过平移,四边形 ABCD 的顶点 A 移到点 A′处,作出平移后的四边形.
随堂练习
1.下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
C
2.经过平移的图形与原图形的对应点所连的线段的关系是( )
A.平行
B.相等
C.平行(或在同一条直线上)且相等
D.不确定
C
3.如图,在图形B到图形A的变化过程中,下列描述
正确的是( )
A.向上平移2个单位长度,向左平移4个单位长度
B.向上平移1个单位长度,向左平移4个单位长度
C.向上平移2个单位长度,向左平移5个单位长度
D.向上平移1个单位长度,向左平移5个单位长度
B
4.(中考·泰州)如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则三角形ABC平移的距离为________cm.
2.5
拓展提升
1.如图,将三角形ABC 向右平移得到三角形DEF,已知
A,D 两点的距离为 1,CE=2,则 BF 的长为( )
A.5
B.4
C.3
D.2
B
B
E
C
F
A
D
2.如图所示,将三角形ABC平移到三角形DEF的位置,则下列结论:①AB∥DE,AD=CF=BE;
②∠ACB=∠DEF;
③平移的方向是点C到点E的方向;
④平移距离为线段BE的长.
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
B
3.如图,将直角三角形 ABC 沿 CB 方向平移得到直角三角形 DEF,已知∠ABC =90°,AG =2,BE =4,DE =6,求阴影部分的面积.
解:∵ 三角形 DEF 是三角形 ABC经过平移得到的,
∴ AB =DE =6,S三角形DEF=S三角形ABC,
∴ BG =ABAG=62=4,
∴ S阴影部分=S梯形BEDG= (BG+DE)·BE= ×(4+6)×4=20.
4.如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,求这块草地的绿地面积.
解:绿地面积为(a-1)b=(ab-b)m2.
归纳小结
平移
概念
两要素
性质
作图
平移的方向、平移的距离
平移前后图形的形状和大小完全相同
对应线段平行(或在同一直线上)且相等
对应点所连线段平行(或在同一直线上)且相等
一定、二找、三移、四连、五写
第七章 相交线与平行线
7. 6 图形的平移
学习目标
1.理解平移的概念及决定因素.
2.会找出平移前后图形中对应点、对应角和对应线段.
3.掌握平移的性质及其运用.
学习重难点
掌握平移的性质及其运用.
理解平移的概念及决定因素.
难点
重点
回顾复习
小学阶段我们学习了哪些图形的变换方法?
平移、轴对称和旋转.
创设情境
仔细观察下面一些美丽的图案,它们有什么共同的特点 能否根据其中的一部分绘制出整个图案?
新知引入
知识点1 平移的定义
如何在一张半透明的纸上,画出一排形状和大小如图的雪人呢?
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个
比较:画出的这些小雪人和已知的图片.
说一说:什么改变了?什么没改变?
1. 把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
归纳
第2个,第3个雪人,…,都可以看成是第1个雪人沿某一直线方向移动得到的.
位置不同的原因是什么?
如何刻画它们移动的距离?
它们移动的距离不同.
鼻尖A与A'叫做对应点,同样,帽顶B与B',钮扣C与C' 都是对应点.
你能在图中再找出几对对应点吗?
A
A
'
B
C
B
'
C
'
思考
把对应点分别连接起来,这些线段有怎样的关系呢?
可以发现:
AA′∥BB′∥CC′,
且AA′ = BB′ = CC′.
再作出连接其他对应点的线段,仍有前面的关系吗?
A
A
'
B
C
B
'
C
'
有
2. 连接各组对应点的线段平行(或在同一条直线上)且相等.
归纳
图形的这种移动,叫做平移(translation).
A
A
'
B
C
B
'
C
'
观察以下几种移动,想一想平移有什么要素?
平移的要素:1. 平移的方向;2. 平移的距离.
注意:图形平移的方向可以是任意指定的方向,不限于是水平的或竖直的,但必须是直线方向.
图形的平移是整个图形都在移动,即图形中所有点、线平移的方向和平移的距离都相同,所以确定一个图形平移的方向和距离,只需确定图形上一个点平移的方向和距离即可.
例题示范
例1 将如图所示的图案平移后,可以得到的图案是( )
A
例2 下列现象:
(1)水平运输带上砖块的运动;
(2)高楼电梯上上下下迎接乘客;
(3)健身做呼啦圈运动;
(4)火车飞驰在一段平直的铁轨上;
(5)沸水中气泡的运动.
属于平移的是___________________.
(1)(2)(4)
新知引入
知识点2 平移的性质
如图,把三角形ABC 沿直线 PQ 平移,得到三角形DEF. 分析 AD、BE、CF 有怎样的数量关系和位置关系.
F
D
A
B
C
P
Q
E
AD//BE//CF, AD=BE=CF.
再画一些连接其他对应点的线段,你能得到什么结论?
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点. 连接各组对应点的线段平行(或在同一条直线上)且相等.
如图,把三角形ABC 沿直线 PQ 平移,得到三角形DEF. 分析对应线段间有怎样的数量关系和位置关系?对应角有什么关系?
F
D
A
B
C
P
Q
E
平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
注意:“连接各组对应点的线段”是原图形上的点与平移后的图形上的点连接而成的;而“对应线段”就存在于原来的图形与平移后的图形之中,是图形的一部分.
平移的性质
1. 平移后得到的新图形与原图形的形状、大小完全相同;
2. 连接各组对应点的线段平行(或在同一条直线上)且相等.
3. 平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
例题示范
例 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE之间有什么数量关系?
导引:
根据平移的特征可知:平移只改变图形的位置,不改变图形的大小;平移得到的图形与原来的图形是完全一样的,所以对应的线段之间是平行且相等的.
解: (1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
新知引入
知识点3 平移作图
如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
解:如图,连接AA' ,过点B作的平行线l,在l 上截取BB' =AA' ,则点B'就是点B的对应点.
类似地,作出点C的对应点 C' ,得到平移后的△A'B'C'.
B'
l
C'
1. 定:确定平移的方向和距离;
2. 找:找出确定图形形状的关键点;
3. 移:按平移的方向和距离平移各个关键点,
得到各个关键点的对应点;
4. 连:按原图形的顺序依次连接各对应点;
5. 写:写出结论.
平移作图的基本步骤
1. 平移的性质是平移作图的依据.
2. 确定一个图形平移后的位置需三个条件:
① 图形原来的位置;
② 平移的方向;
③ 平移的距离.
这三个条件缺一不可,只有这样,平移后的图形才唯一确定.
例题示范
例 如图所示,经过平移,四边形 ABCD 的顶点 A 移到点 A′处,作出平移后的四边形.
随堂练习
1.下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
C
2.经过平移的图形与原图形的对应点所连的线段的关系是( )
A.平行
B.相等
C.平行(或在同一条直线上)且相等
D.不确定
C
3.如图,在图形B到图形A的变化过程中,下列描述
正确的是( )
A.向上平移2个单位长度,向左平移4个单位长度
B.向上平移1个单位长度,向左平移4个单位长度
C.向上平移2个单位长度,向左平移5个单位长度
D.向上平移1个单位长度,向左平移5个单位长度
B
4.(中考·泰州)如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则三角形ABC平移的距离为________cm.
2.5
拓展提升
1.如图,将三角形ABC 向右平移得到三角形DEF,已知
A,D 两点的距离为 1,CE=2,则 BF 的长为( )
A.5
B.4
C.3
D.2
B
B
E
C
F
A
D
2.如图所示,将三角形ABC平移到三角形DEF的位置,则下列结论:①AB∥DE,AD=CF=BE;
②∠ACB=∠DEF;
③平移的方向是点C到点E的方向;
④平移距离为线段BE的长.
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
B
3.如图,将直角三角形 ABC 沿 CB 方向平移得到直角三角形 DEF,已知∠ABC =90°,AG =2,BE =4,DE =6,求阴影部分的面积.
解:∵ 三角形 DEF 是三角形 ABC经过平移得到的,
∴ AB =DE =6,S三角形DEF=S三角形ABC,
∴ BG =ABAG=62=4,
∴ S阴影部分=S梯形BEDG= (BG+DE)·BE= ×(4+6)×4=20.
4.如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,求这块草地的绿地面积.
解:绿地面积为(a-1)b=(ab-b)m2.
归纳小结
平移
概念
两要素
性质
作图
平移的方向、平移的距离
平移前后图形的形状和大小完全相同
对应线段平行(或在同一直线上)且相等
对应点所连线段平行(或在同一直线上)且相等
一定、二找、三移、四连、五写
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
