8.3 同底数幂的除法 课件 (共17张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 8.3 同底数幂的除法 课件 (共17张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 663.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第八章 整式的乘法
8.3 同底数幂的除法
学习目标
1.掌握同底数幂的运算性质,会用同底数幂的运算进行有关计算.
2.了解零指数幂和负整指数幂的意义.
3.体会转化,整体思想的应用.
学习重难点
掌握同底数幂的运算性质,会用同底数幂的运算进行有关计算.
掌握同底数幂的运算性质,会用同底数幂的运算进行有关计算.
难点
重点
回顾复习
积的乘方运算法则:
(ab)n = a n ·bn (n 为正整数)
同底数幂的乘法运算法则:
a m·a n=a m+n (m,n 都是正整数)
幂的乘方运算法则:
(a m)n = a mn (m,n 都是正整数)
新知引入
知识点 同底数幂的除法法则
1.计算下列各题,用幂的形式表示结果,并说明计算的依据.
(1) 55÷53 =______________.
(2) (-3)5+(-3)3=______________.
(3)如果a≠0,那么a6÷a3=______________.
(4)如果a≠0,那么a10÷a4=______________.
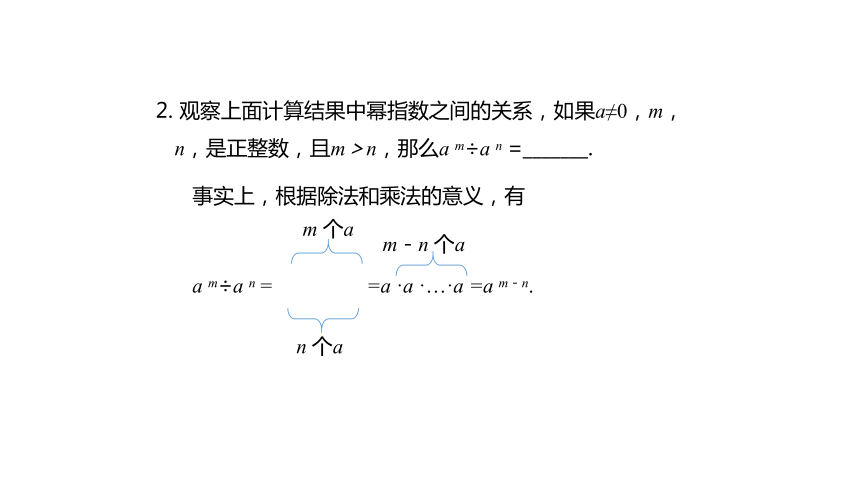
2. 观察上面计算结果中幂指数之间的关系,如果a≠0,m,n,是正整数,且m>n,那么a m÷a n =_______.
事实上,根据除法和乘法的意义,有
a m÷a n = =a ·a ·…·a =a m-n.
m 个a
n 个a
m-n 个a
a m÷a n =a m-n (a≠0,m,n,是正整数,且m>n) .
同底数幂相除,底数不变,指数相减.
归纳
观察与思考:
问题:我们得到了同底数幂的除法当“m>n”时的运算性质,那么,对于这个性质,你有什么疑问吗?
当“m≤n”时又该如何计算呢?上述性质还适用吗?
1.按乘方的意义和除法计算:
(1)当 时,
(2)当 时,
如果按照前面m>n时得出的结论就有:
比较它们的结果就应该有:
因此我们规定:
(1) ,即任何不等于0的数的0次幂都等于 ;
(2) 是正整数)即任何不等于0的数的 次幂,等于这个数的倒数。
从而对于任意正整数m,n,都有:
即:同底数幂相除,底数不变,指数相减.
例题示范
例(独立完成,组内互查)
(1)
(2)
(3)
(4)
随堂练习
1
下面的运算是否正确?如果不正确,请改正过来.
(1) a 4÷a 3 =a 7; (2) a 6÷a 3 =a 2.
(1)不正确,应为a 4÷a 3=a 4-3=a.
(2)不正确,应为a 6÷a 3=a 6-3=a 3.
解:
计算:
(1) a 6÷a 4; (2) (-10)8÷(-10)4 .
计算108÷103 .
(1)a 6÷a 4=a 6-4=a 2.
(2)(-10)8÷(-10)4=(-10)8-4=(-10)4=104.
解:
2
3
108÷103=108-3=105.
解:
计算x 6÷x 2正确的结果是( )
A.3 B.x 3
C.x 4 D.x 8
下列计算正确的是( )
A.a 3+a 2=a 5 B.a 3·a 2=a 5
C.(a3)2=a 5 D.a 6÷a 2=a 3
下列运算正确的是( )
A.m 6÷m 2=m 3 B.3m 2-2m 2=m 2
C.(3m 2)3=9m 6 D.m ·m 2=m 2
4
C
B
5
6
B
拓展提升
计算:
(1)[(x n+1)4·x 2]÷[(x n+2)3÷(x 2)n];
(2) (a ·a m+1)2-(a 2)m+3÷a 2.
(1)原式=x 4n+4+2÷(x 3n+6÷x 2n)
=x 4n+6÷x n+6
=x 3n.
(2)原式=a 2m+4-a 2m+6÷a 2
=a 2m+4-a 2m+4
=0.
解:
1
先化简,再求值:(2x-y )13÷[(2x-y )3]2÷[(y-2x )2]3,
其中x=2,y=-1.
原式=(2x-y )13÷(2x-y )6÷(2x-y )6
=(2x-y )13-6-6
=2x-y,
当x=2,y=-1时,
原式=2×2-(-1)=5.
解:
2
已知:3a=4,3b=10,3c=25.
(1)求32a 的值;
(2)求3c-b+a 的值;
(3)试说明:2b=a+c.
(1)32a=(3a)2=42=16.
(2)3c-b+a=3c÷3b×3a=25÷10×4=10.
(3)因为32b=(3b)2=102=100,
3a+c=3a×3c=4×25=100,
所以32b=3a+c,所以2b=a+c.
解:
3
归纳小结
第八章 整式的乘法
8.3 同底数幂的除法
学习目标
1.掌握同底数幂的运算性质,会用同底数幂的运算进行有关计算.
2.了解零指数幂和负整指数幂的意义.
3.体会转化,整体思想的应用.
学习重难点
掌握同底数幂的运算性质,会用同底数幂的运算进行有关计算.
掌握同底数幂的运算性质,会用同底数幂的运算进行有关计算.
难点
重点
回顾复习
积的乘方运算法则:
(ab)n = a n ·bn (n 为正整数)
同底数幂的乘法运算法则:
a m·a n=a m+n (m,n 都是正整数)
幂的乘方运算法则:
(a m)n = a mn (m,n 都是正整数)
新知引入
知识点 同底数幂的除法法则
1.计算下列各题,用幂的形式表示结果,并说明计算的依据.
(1) 55÷53 =______________.
(2) (-3)5+(-3)3=______________.
(3)如果a≠0,那么a6÷a3=______________.
(4)如果a≠0,那么a10÷a4=______________.
2. 观察上面计算结果中幂指数之间的关系,如果a≠0,m,n,是正整数,且m>n,那么a m÷a n =_______.
事实上,根据除法和乘法的意义,有
a m÷a n = =a ·a ·…·a =a m-n.
m 个a
n 个a
m-n 个a
a m÷a n =a m-n (a≠0,m,n,是正整数,且m>n) .
同底数幂相除,底数不变,指数相减.
归纳
观察与思考:
问题:我们得到了同底数幂的除法当“m>n”时的运算性质,那么,对于这个性质,你有什么疑问吗?
当“m≤n”时又该如何计算呢?上述性质还适用吗?
1.按乘方的意义和除法计算:
(1)当 时,
(2)当 时,
如果按照前面m>n时得出的结论就有:
比较它们的结果就应该有:
因此我们规定:
(1) ,即任何不等于0的数的0次幂都等于 ;
(2) 是正整数)即任何不等于0的数的 次幂,等于这个数的倒数。
从而对于任意正整数m,n,都有:
即:同底数幂相除,底数不变,指数相减.
例题示范
例(独立完成,组内互查)
(1)
(2)
(3)
(4)
随堂练习
1
下面的运算是否正确?如果不正确,请改正过来.
(1) a 4÷a 3 =a 7; (2) a 6÷a 3 =a 2.
(1)不正确,应为a 4÷a 3=a 4-3=a.
(2)不正确,应为a 6÷a 3=a 6-3=a 3.
解:
计算:
(1) a 6÷a 4; (2) (-10)8÷(-10)4 .
计算108÷103 .
(1)a 6÷a 4=a 6-4=a 2.
(2)(-10)8÷(-10)4=(-10)8-4=(-10)4=104.
解:
2
3
108÷103=108-3=105.
解:
计算x 6÷x 2正确的结果是( )
A.3 B.x 3
C.x 4 D.x 8
下列计算正确的是( )
A.a 3+a 2=a 5 B.a 3·a 2=a 5
C.(a3)2=a 5 D.a 6÷a 2=a 3
下列运算正确的是( )
A.m 6÷m 2=m 3 B.3m 2-2m 2=m 2
C.(3m 2)3=9m 6 D.m ·m 2=m 2
4
C
B
5
6
B
拓展提升
计算:
(1)[(x n+1)4·x 2]÷[(x n+2)3÷(x 2)n];
(2) (a ·a m+1)2-(a 2)m+3÷a 2.
(1)原式=x 4n+4+2÷(x 3n+6÷x 2n)
=x 4n+6÷x n+6
=x 3n.
(2)原式=a 2m+4-a 2m+6÷a 2
=a 2m+4-a 2m+4
=0.
解:
1
先化简,再求值:(2x-y )13÷[(2x-y )3]2÷[(y-2x )2]3,
其中x=2,y=-1.
原式=(2x-y )13÷(2x-y )6÷(2x-y )6
=(2x-y )13-6-6
=2x-y,
当x=2,y=-1时,
原式=2×2-(-1)=5.
解:
2
已知:3a=4,3b=10,3c=25.
(1)求32a 的值;
(2)求3c-b+a 的值;
(3)试说明:2b=a+c.
(1)32a=(3a)2=42=16.
(2)3c-b+a=3c÷3b×3a=25÷10×4=10.
(3)因为32b=(3b)2=102=100,
3a+c=3a×3c=4×25=100,
所以32b=3a+c,所以2b=a+c.
解:
3
归纳小结
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
