9.2 三角形的内角 第2课时 课件 (共31张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 9.2 三角形的内角 第2课时 课件 (共31张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 932.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 21:44:49 | ||
图片预览





文档简介
(共31张PPT)
第九章 三角形
9.2 三角形的内角
第2课时
学习目标
1.了解三角形外角的概念,能在图形中找出外角.
2.掌握三角形外角与内角关系,能按边和角对三角形分类,渗透分类思想.
学习重难点
掌握三角形外角与内角关系,能按边和角对三角形分类,渗透分类思想.
掌握三角形外角与内角关系,能按边和角对三角形分类,渗透分类思想.
难点
重点
复习导入
48 °
1.在△ABC中,∠A=80°, ∠B=52°,则∠C= .
3.什么是三角形的内角?其内角和等于多少?
三角形相邻两边组成的角叫作三角形的内角,
它们的和是180 °.
2.如图,在△ABC中, ∠A=70°, ∠B=60°,
则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
新知引入
知识点1 三角形外角的概念
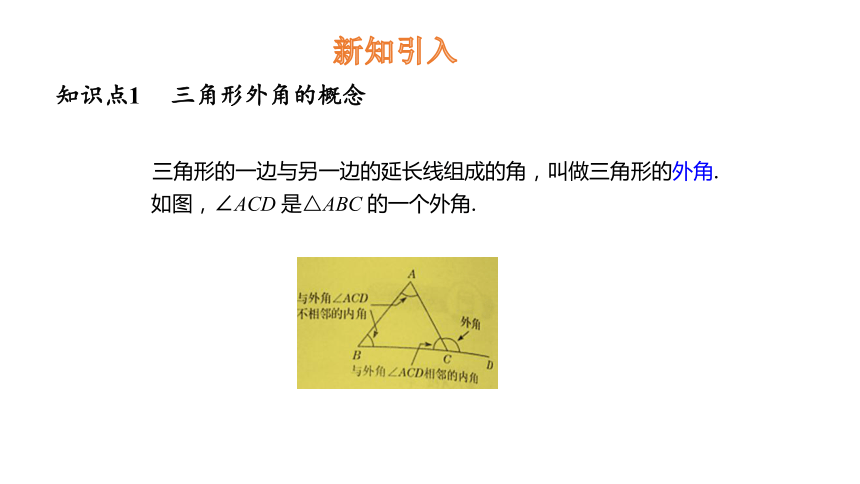
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
如图,∠ACD 是△ABC 的一个外角.
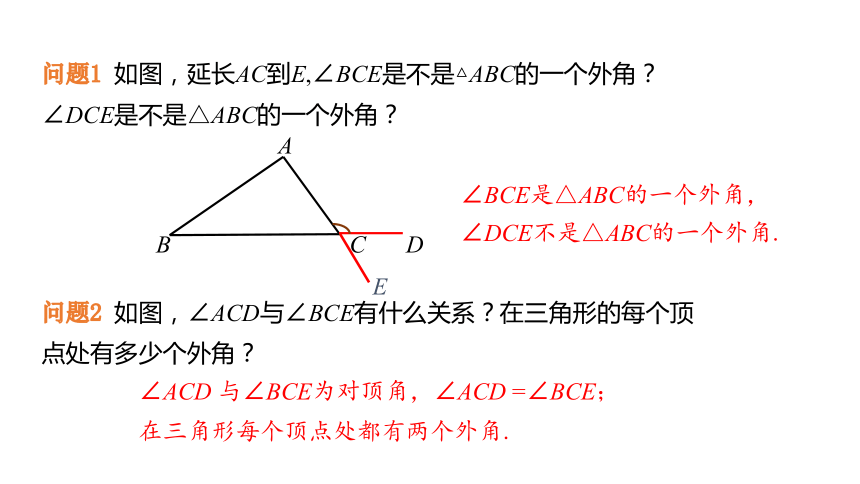
问题1 如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
问题2 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
A
B
C
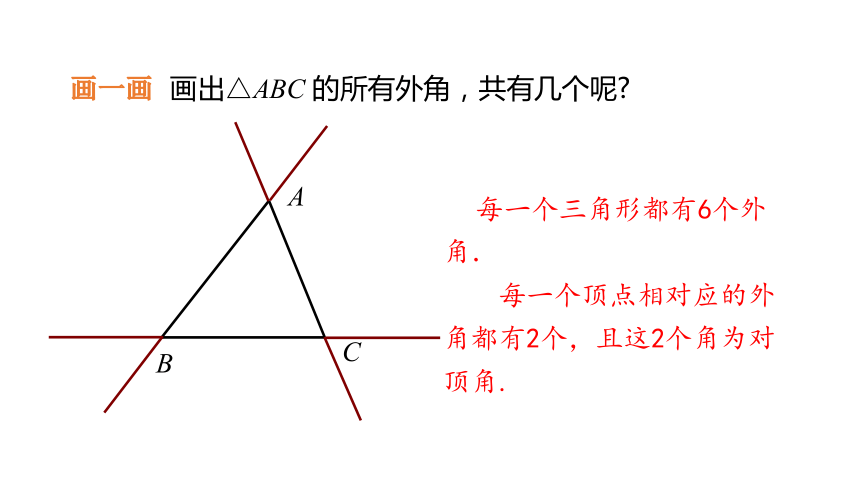
画一画 画出△ABC 的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,且这2个角为对顶角.
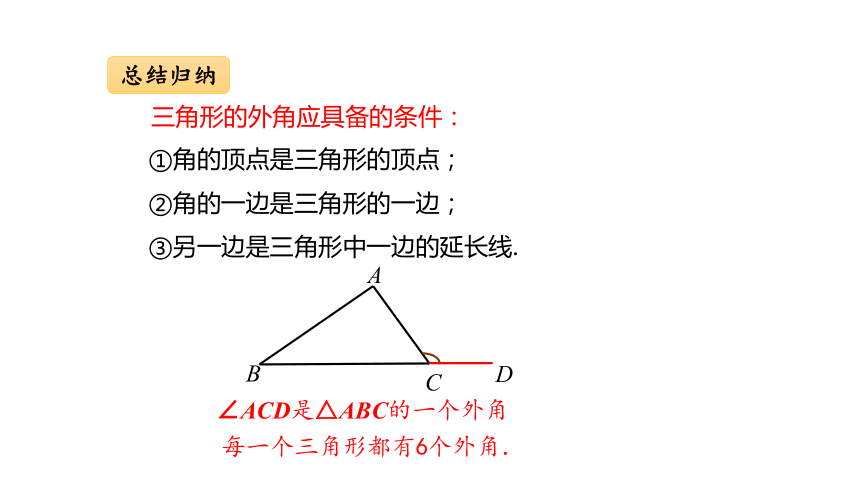
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
总结归纳
例题示范
例1
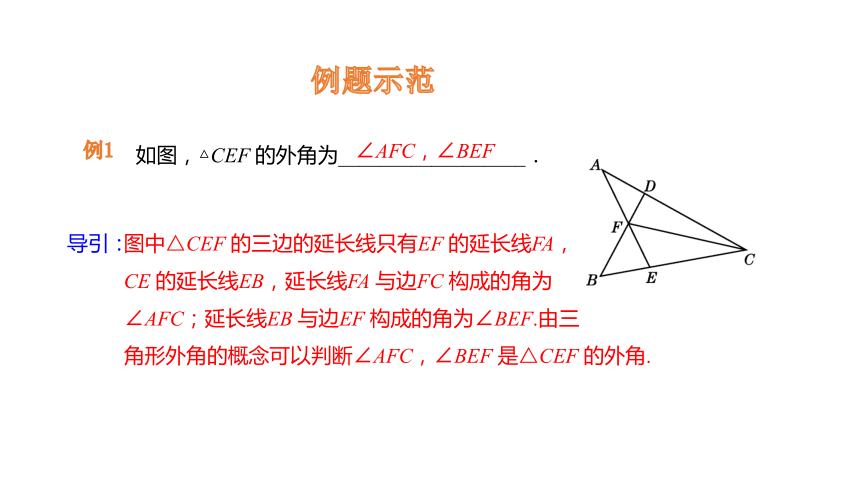
如图,△CEF 的外角为__________________.
图中△CEF 的三边的延长线只有EF 的延长线FA,
CE 的延长线EB,延长线FA 与边FC 构成的角为
∠AFC;延长线EB 与边EF 构成的角为∠BEF.由三
角形外角的概念可以判断∠AFC,∠BEF 是△CEF 的外角.
导引:
∠AFC,∠BEF
总结
判定一个角是三角形的外角的三个条件:一
是顶点在三角形的一个顶点上;二是一边是三角
形的一条边;三是另一边是三角形的另一条边的
延长线.
知识点2 三角形外角的性质
三角形的外角
A
C
B
D
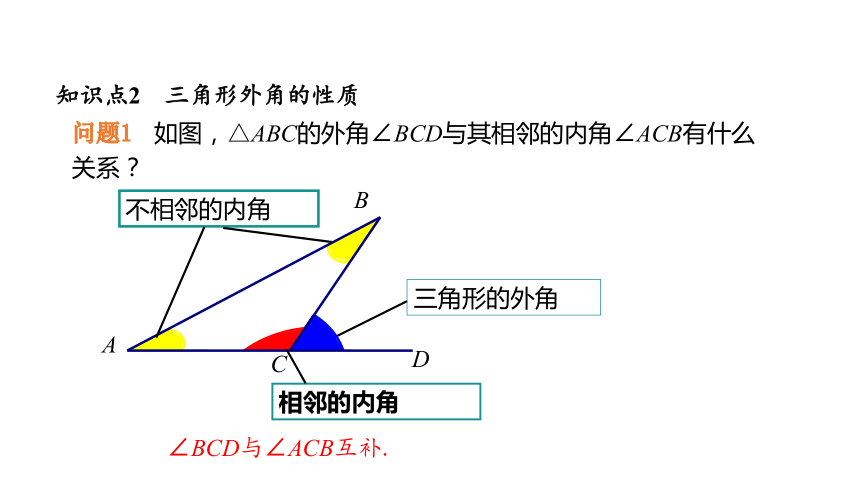
相邻的内角
不相邻的内角
问题1 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
∠BCD与∠ACB互补.
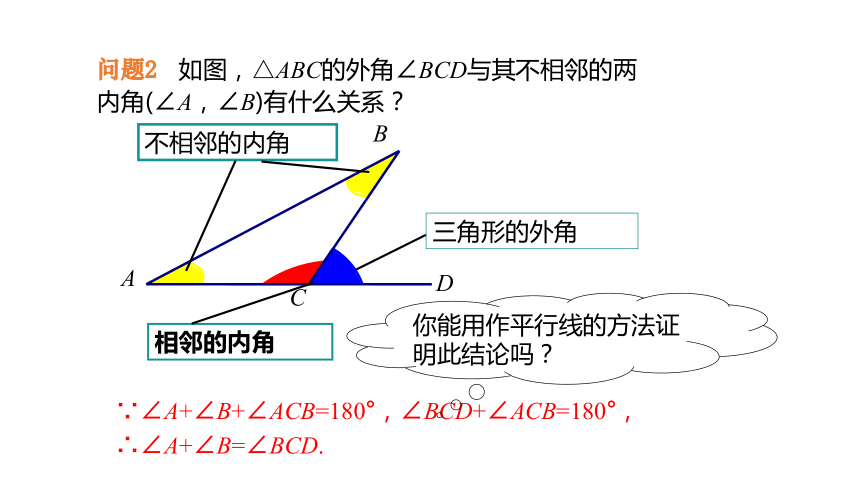
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
D
证明:过C 作CE 平行于AB,
A
B
C
1
2
∴∠1= ∠B(两直线平行,同位角相等),
∠2= ∠A (两直线平行,内错角相等),
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
如图 ,试比较∠2 、∠1的大小;
如图 ,试比较∠3 、∠2、 ∠1的大小.
图
图
解:∵∠2=∠1+∠B,
∴∠2>∠1.
解:∵∠2=∠1+∠B,
∠3=∠2+∠D,
∴∠3>∠2>∠1.
想一想
三角形的一个外角等于与它不相邻的两个内角之和.
三角形的一个外角大于与它不相邻的任意一个内角.
A
B
C
D
∠B+∠C=∠CAD
∠CAD > ∠B, ∠CAD > ∠C
归纳总结
三角形外角的性质
如图,∠BCD=92°,∠A=27°,∠BED=44°. 求:(1)∠B 的度数;
(2)∠BFD 的度数.
例2
(1)在△ABC 中,
∵ ∠BCD=∠A+∠B (三角形的一个外角等
于与它不相邻的两个内角的和).
∴∠B =∠BCD-∠A = 92°-27°=65°.
(2)在△BEF 中,
∵ ∠BFD=∠A+∠BED (三角形的一个外角等
于与它不相邻的两个内角的和).
∠BED=44°(已知),∠B=65°(已求).
∴∠BFD=44°+65°=109°.
解:
总结
利用三角形的外角的性质求角的度数常与内角的
度数相结合来应用.
知识点3 三角形的分类
互动探究
填空
(1)一个三角形最多有 个直角,
因为 ;
(2)一个三角形最多有 个钝角,
因为 ;
(3)一个三角形至少有 个锐角,
因为 .
1
1
2
三角形内角和等于180 °
三角形内角和等于180 °
三角形内角和等于180 °
问题:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
知识要点
锐角三角形
直角三角形
钝角三角形
按是否有边相等分
按内角大小分
三角形
三角形的分类
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
如果一个三角形三个内角度数的比为2 : 3 : 5,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
例3
导引:
设三角形三个内角的度数分别为2x,3x,5x,由
三角形的内角和等于180°,可列出方程2x+3x
+5x=180°,解得x=18°,∴三角形最大的内
角是5x=90°,故这个三角形是直角三角形.
A
利用方程思想解决问题,用未知数分别表示出三个内角的度数,再利用三角形内角和定理列出方程,
解方程求出未知数的值,进一步求出最大内角,再进
行判断即可.
总结
随堂练习
1.如果三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
2.已知,如图,△ABC 中,∠B=∠DAC,则∠BAC 和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
B
B
3.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F
等于( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中 ,
∠C+∠1+∠2=180 ,
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180 .
4.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
拓展提升
下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
C
1
2
如图,在△ABC 中,D 是三角形内一点,
试说明:∠BDC >∠A.
如图,延长BD 交AC 于点E.
因为在△ABE 中,∠BEC>∠A,
在△CDE 中,∠BDC>∠BEC,
所以∠BDC>∠A.
解:
如图,在△ABC 中,D 为BC 的延长线上一点,∠A=60°,
∠ABC 和∠ACD 的平分线交于点O,求∠O 的度数.
由题意得∠OBC= ∠ABC,
∠DCO= ∠ACD,
∴∠O=∠DCO-∠OBC= ∠ACD- ∠ABC=
(∠ACD-∠ABC )= ∠A=30°.
解:
3
4
一个零件的形状如图所示,按规定∠A 应等于90°,
∠B 和∠C 分别是21°和20°,质量检验员量得∠BDC=
130°后就断定这个零件不合格.请说明为什么?
如图,连接AD 并延长到点E,
则∠CDE=∠C+∠2,
∠BDE=∠B+∠1.
所以∠CDE+∠BDE=∠C+∠2+∠B+∠1.
即∠BDC=∠C+∠B+∠CAB.
若零件合格,则∠BDC=20°+21°+90°=131°.
而量得∠BDC=130°,所以这个零件不合格.
解:
归纳小结
三角形的外角
三角形外角的性质
三角形的分类
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
按边分类
按角分类
等腰三角形
不等边三角形
锐角三角形
直角三角形
钝角三角形
第九章 三角形
9.2 三角形的内角
第2课时
学习目标
1.了解三角形外角的概念,能在图形中找出外角.
2.掌握三角形外角与内角关系,能按边和角对三角形分类,渗透分类思想.
学习重难点
掌握三角形外角与内角关系,能按边和角对三角形分类,渗透分类思想.
掌握三角形外角与内角关系,能按边和角对三角形分类,渗透分类思想.
难点
重点
复习导入
48 °
1.在△ABC中,∠A=80°, ∠B=52°,则∠C= .
3.什么是三角形的内角?其内角和等于多少?
三角形相邻两边组成的角叫作三角形的内角,
它们的和是180 °.
2.如图,在△ABC中, ∠A=70°, ∠B=60°,
则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
新知引入
知识点1 三角形外角的概念
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
如图,∠ACD 是△ABC 的一个外角.
问题1 如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
问题2 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
A
B
C
画一画 画出△ABC 的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,且这2个角为对顶角.
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
总结归纳
例题示范
例1
如图,△CEF 的外角为__________________.
图中△CEF 的三边的延长线只有EF 的延长线FA,
CE 的延长线EB,延长线FA 与边FC 构成的角为
∠AFC;延长线EB 与边EF 构成的角为∠BEF.由三
角形外角的概念可以判断∠AFC,∠BEF 是△CEF 的外角.
导引:
∠AFC,∠BEF
总结
判定一个角是三角形的外角的三个条件:一
是顶点在三角形的一个顶点上;二是一边是三角
形的一条边;三是另一边是三角形的另一条边的
延长线.
知识点2 三角形外角的性质
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
问题1 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
∠BCD与∠ACB互补.
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
D
证明:过C 作CE 平行于AB,
A
B
C
1
2
∴∠1= ∠B(两直线平行,同位角相等),
∠2= ∠A (两直线平行,内错角相等),
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
如图 ,试比较∠2 、∠1的大小;
如图 ,试比较∠3 、∠2、 ∠1的大小.
图
图
解:∵∠2=∠1+∠B,
∴∠2>∠1.
解:∵∠2=∠1+∠B,
∠3=∠2+∠D,
∴∠3>∠2>∠1.
想一想
三角形的一个外角等于与它不相邻的两个内角之和.
三角形的一个外角大于与它不相邻的任意一个内角.
A
B
C
D
∠B+∠C=∠CAD
∠CAD > ∠B, ∠CAD > ∠C
归纳总结
三角形外角的性质
如图,∠BCD=92°,∠A=27°,∠BED=44°. 求:(1)∠B 的度数;
(2)∠BFD 的度数.
例2
(1)在△ABC 中,
∵ ∠BCD=∠A+∠B (三角形的一个外角等
于与它不相邻的两个内角的和).
∴∠B =∠BCD-∠A = 92°-27°=65°.
(2)在△BEF 中,
∵ ∠BFD=∠A+∠BED (三角形的一个外角等
于与它不相邻的两个内角的和).
∠BED=44°(已知),∠B=65°(已求).
∴∠BFD=44°+65°=109°.
解:
总结
利用三角形的外角的性质求角的度数常与内角的
度数相结合来应用.
知识点3 三角形的分类
互动探究
填空
(1)一个三角形最多有 个直角,
因为 ;
(2)一个三角形最多有 个钝角,
因为 ;
(3)一个三角形至少有 个锐角,
因为 .
1
1
2
三角形内角和等于180 °
三角形内角和等于180 °
三角形内角和等于180 °
问题:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
知识要点
锐角三角形
直角三角形
钝角三角形
按是否有边相等分
按内角大小分
三角形
三角形的分类
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
如果一个三角形三个内角度数的比为2 : 3 : 5,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
例3
导引:
设三角形三个内角的度数分别为2x,3x,5x,由
三角形的内角和等于180°,可列出方程2x+3x
+5x=180°,解得x=18°,∴三角形最大的内
角是5x=90°,故这个三角形是直角三角形.
A
利用方程思想解决问题,用未知数分别表示出三个内角的度数,再利用三角形内角和定理列出方程,
解方程求出未知数的值,进一步求出最大内角,再进
行判断即可.
总结
随堂练习
1.如果三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
2.已知,如图,△ABC 中,∠B=∠DAC,则∠BAC 和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
B
B
3.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F
等于( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中 ,
∠C+∠1+∠2=180 ,
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180 .
4.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
拓展提升
下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
C
1
2
如图,在△ABC 中,D 是三角形内一点,
试说明:∠BDC >∠A.
如图,延长BD 交AC 于点E.
因为在△ABE 中,∠BEC>∠A,
在△CDE 中,∠BDC>∠BEC,
所以∠BDC>∠A.
解:
如图,在△ABC 中,D 为BC 的延长线上一点,∠A=60°,
∠ABC 和∠ACD 的平分线交于点O,求∠O 的度数.
由题意得∠OBC= ∠ABC,
∠DCO= ∠ACD,
∴∠O=∠DCO-∠OBC= ∠ACD- ∠ABC=
(∠ACD-∠ABC )= ∠A=30°.
解:
3
4
一个零件的形状如图所示,按规定∠A 应等于90°,
∠B 和∠C 分别是21°和20°,质量检验员量得∠BDC=
130°后就断定这个零件不合格.请说明为什么?
如图,连接AD 并延长到点E,
则∠CDE=∠C+∠2,
∠BDE=∠B+∠1.
所以∠CDE+∠BDE=∠C+∠2+∠B+∠1.
即∠BDC=∠C+∠B+∠CAB.
若零件合格,则∠BDC=20°+21°+90°=131°.
而量得∠BDC=130°,所以这个零件不合格.
解:
归纳小结
三角形的外角
三角形外角的性质
三角形的分类
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
按边分类
按角分类
等腰三角形
不等边三角形
锐角三角形
直角三角形
钝角三角形
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
