9.3 三角形的角平分线、中线和高 课件 (共30张PPT) 2023-2024学年数学冀教版七年级下册
文档属性
| 名称 | 9.3 三角形的角平分线、中线和高 课件 (共30张PPT) 2023-2024学年数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 808.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
第九章 三角形
9.3 三角形的角平分线、中线和高
学习目标
1.理解三角形的角平分线、中线、高线的概念.
2.会画出已知三角形的角平分线、中线和高.
3.掌握“三线”的性质,并能应用进行计算.
学习重难点
掌握“三线”的性质,并能应用进行计算.
掌握“三线”的性质,并能应用进行计算.
难点
重点
复习导入
上节课我们学习三角形按角分为哪几类?
1.锐角三角形;2.直角三角形;3.钝角三角形。
新知引入
知识点1 三角形的角平分线
1.复习用量角器或折纸的办法画出或折出一个角的平分线。
角平分线的定义及画法:
从一个角的顶点引出的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线。
A
B
C
D
定义:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫三角形的角平分线。
角平分线的符号语言:
∵ AD是△ABC的角平分线
∴∠BAD=∠CAD= ∠BAC
2.什么是三角形的角平分线?
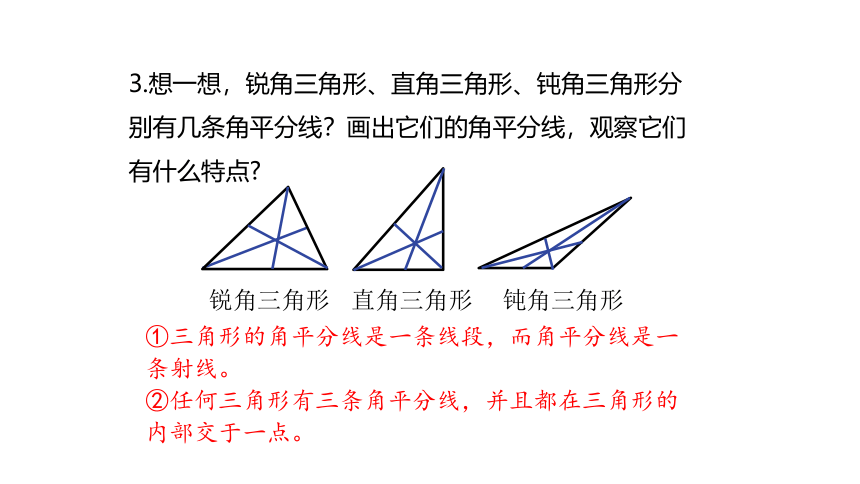
3.想一想,锐角三角形、直角三角形、钝角三角形分别有几条角平分线?画出它们的角平分线,观察它们有什么特点
锐角三角形
钝角三角形
直角三角形
①三角形的角平分线是一条线段,而角平分线是一条射线。
②任何三角形有三条角平分线,并且都在三角形的内部交于一点。
例题示范
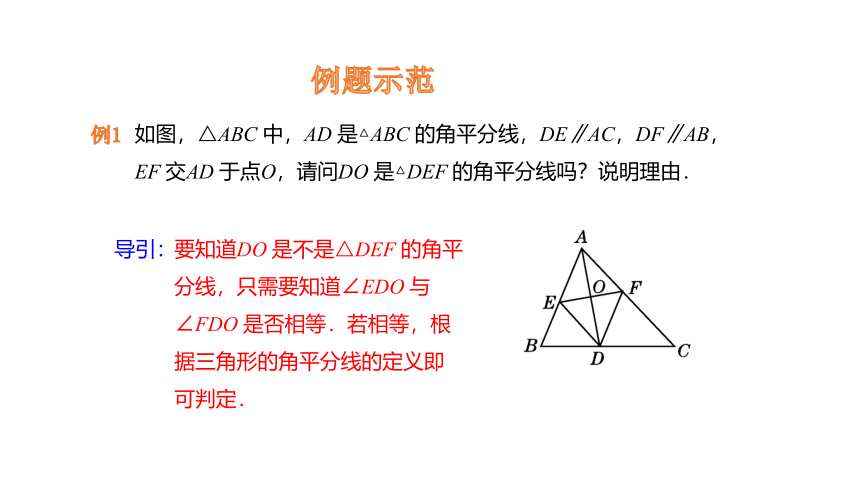
要知道DO 是不是△DEF 的角平
分线,只需要知道∠EDO 与
∠FDO 是否相等.若相等,根
据三角形的角平分线的定义即
可判定.
例1
如图,△ABC 中,AD 是△ABC 的角平分线,DE∥AC,DF∥AB,EF 交AD 于点O,请问DO 是△DEF 的角平分线吗?说明理由.
导引:
DO 是△DEF 的角平分线.理由如下:
因为AD是△ABC 的角平分线,
所以∠DAB=∠DAC (角平分线定义).
因为DE∥AC,DF∥AB,
所以∠DAC=∠ADE,∠DAB=∠ADF (两直线平行,内错角相等),所以∠ADE=∠ADF (等量代换),
所以DO 是△DEF 的角平分线.
解:
总结
本例在解题过程中,先利用角平分线的定义,得出相等的角,再结合相关条件(如平行等)推出新的一组相等的角,最后由角平分线的定义说明角平分线,它经历了定义→条件→定义的过程,这就是定义法.
知识点2 三角形的中线
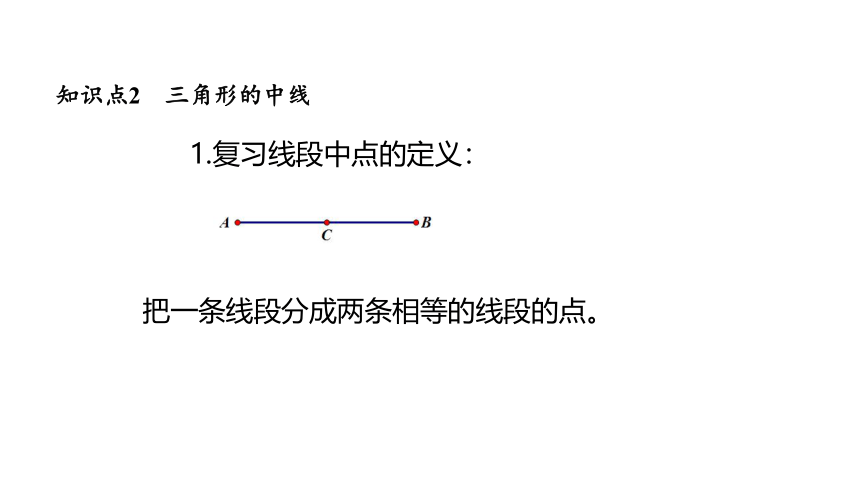
1.复习线段中点的定义:
把一条线段分成两条相等的线段的点。
A
B
C
D
.
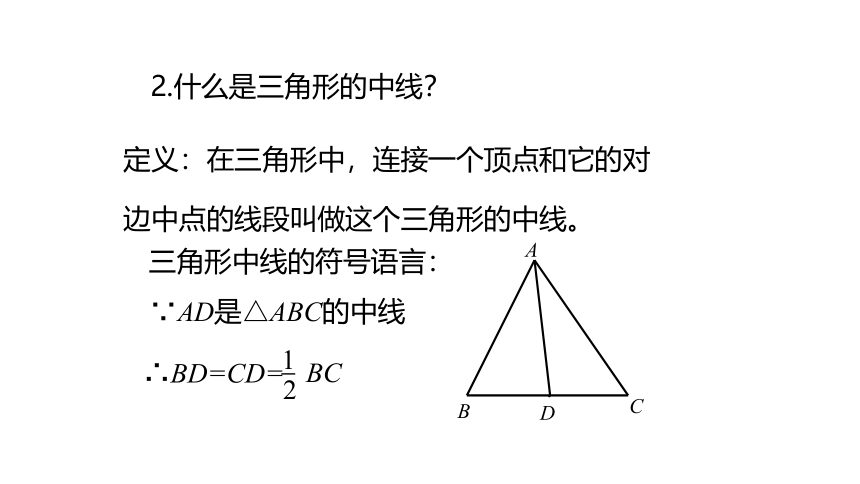
定义:在三角形中,连接一个顶点和它的对边中点的线段叫做这个三角形的中线。
三角形中线的符号语言:
∵AD是△ABC的中线
∴BD=CD=
1
2
BC
2.什么是三角形的中线?
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
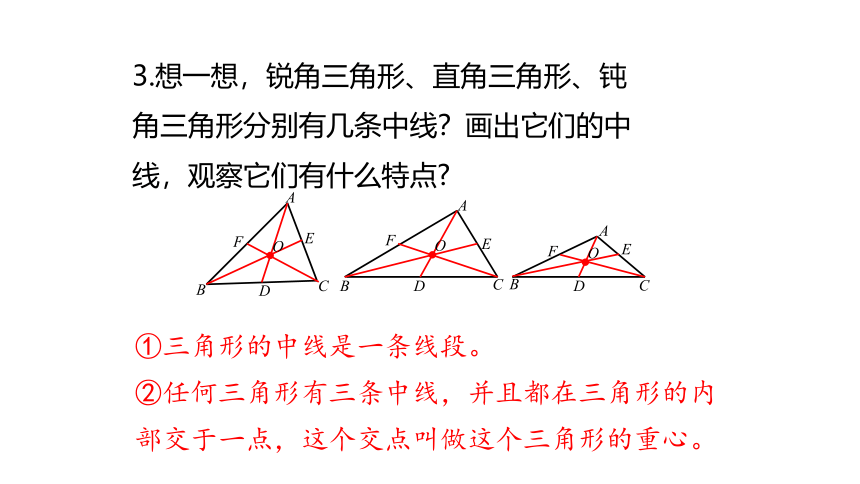
3.想一想,锐角三角形、直角三角形、钝角三角形分别有几条中线?画出它们的中线,观察它们有什么特点
①三角形的中线是一条线段。
②任何三角形有三条中线,并且都在三角形的内部交于一点,这个交点叫做这个三角形的重心。
4.用薄厚均匀的硬纸板裁出一个三角形,画出这个三角形的三条中线,在它们的交点处钻一个小孔,通过小孔系一条线将三角形硬纸板吊起,三角形硬纸板处于什么状态?这种现象说明了什么?
三角形硬纸板处于平衡状态,这种现象说明了重心能使物体保持平衡。
例2
张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.
根据等底同高的三角形的面积相
等,要等分三角形的面积,只需
要作出一条边上的中线即可.
导引:
解:
根据要求,平分田地的直线必须经过三角形的顶点.画△ABC 的中线AD (如图),则AD 就把△ABC 的面积平分成两份.这是因为AD 是△ABC 的中线,所以BD=DC.过点A 作AE⊥BC 于点E.在△ABD 和△ACD 中,因为BD,CD 边上的高都是AE,所以由三角形的面积计算公式,知△ABD 和△ACD 的面积相等,因此,要把△ABC 平分成两个三角形,只需画中线AD 即可,这是一种平分方法.(本题答案不唯一,作AB,AC 边上的中线也可以)
总结
(1)三角形的任意一条中线都能把三角形分成面积相
等的两部分,即等底同高的三角形面积相等;
(2)拓展:在两个三角形中:底、高、面积这三个量,
如果有其中的两个量相等,那么第三个量也相等.
知识点3 三角形的高
1. 复习“过一点作已知直线的垂线”:
A
B
C
定义:三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,简称三角形的高。
D
三角形高的符号语言:
∵AD是△ABC的高
∴AD⊥BC或∠ADC=∠ADB=90°
2.什么是三角形的高线?
3.想一想,锐角三角形、直角三角形、钝角三角形分别有几条高线?画出它们的高线,观察它们有什么特点
①三角形的高是一条线段。
②任何三角形有三条高,三条高(或高的延长线)相交于一点。可分为锐角三角形(内部),直角三角形(直角顶点),钝角三角形(外部)。
画出图中△ABC 的三条高.(要标明字母,不写画法)
例3
导引:
“作一边上的高”,即可看作“过一点(这边所对角的顶点)作已知直线(这边所在的直线)的垂线.”按照“过一点作已知直线的垂线”进行作图,顶点与垂足之间的线段即为该边上的高;需注意AB,BC 边上的高在三角形的外部,作高时先延长AB 与CB.
解:
如图所示.
总结
(1)作三角形的高时,找准顶点和对边是关键,作高的步骤就是“过一点作已知直线的垂线”的步骤:
一靠(三角尺的一条直角边靠在要作高的边上)、
二找(移动三角尺使另一条直角边通过要作高的顶点)、三画线(画垂线段),如图.
(2)注意:高是线段,垂线是直线.
随堂练习
1、下列各组图形中,哪一组图形中AD是△ABC的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A.
B.
C.
D.
2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形
B
D
3、如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35 cm,BC=11 cm,且△ABD与△ACD的周长之差为3 cm,求AB与AC的长.
A
C
D
B
解:∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
又∵△ABD与△ACD的周长之差为3cm,
∴AB-AC=3,
∴AB=13.5cm,AC=10.5cm.
拓展提升
能把三角形平分成两个面积相等的三角形的线段是( )
A.三角形的中线
B.三角形的高
C.三角形的角平分线
D.以上三种情况都正确
A
1
如图,AD 是∠CAB 的平分线,DE∥AB,DF∥AC,EF 交AD 于点O.
请问:
(1)DO 是∠EDF 的平分线吗?
如果是,请给予证明;
如果不是,请说明理由.
(2)若将“DO 是∠EDF 的平分线”与“AD 是∠CAB 的平分线”,“DE∥AB ”,“DF∥AC ”三个条件中的任一条件交换,所得说法正确吗?若正确,请选择一个说明理由.
2
(1)DO 是∠EDF 的平分线.
证明如下:∵AD是∠CAB 的平分线,
∴∠EAD=∠FAD.
∵DE∥AB,DF∥AC,
∴∠EDA=∠FAD,∠FDA=∠EAD.
∴∠EDA=∠FDA.
∴DO 是∠EDF 的平分线.
解:
(2)与三个条件中的任一条件交换,所得说法都正确.
若和“DE∥AB ”交换.
理由如下:∵DF∥AC,∴∠FDA=∠EAD.
∵AD 是∠CAB 的平分线,
∴∠EAD=∠FAD.∴∠FAD=∠FDA.
∵DO 是∠EDF 的平分线,
∴∠EDA=∠FDA.∴∠EDA=∠FAD.
∴DE∥AB.
(答案不唯一)
如图,在△ABC 中,AD⊥BC,BE⊥AC,垂足分别
为D,E,若BC=10,AC=8,BE= ,求AD 的长.
4
∵AD⊥BC,BE⊥AC,
∴S△ABC= ·BC·AD= ·AC·BE.
∴BC ·AD=AC ·BE.
又∵BC=10,AC=8,BE= ,
∴10AD=8× .
∴AD=6.8.
解:
归纳小结
三角形的 重要线段 概念 图示 表述方式
三角形 的高线 从三角形的一个顶点向它的对边所在的直线作垂线,_____和_____之间的 _____
三角形 的中线 三角形中,连结一个顶点和它对边 ____的 ____,三条中线的交点叫做_____
三角形的 角平分线 三角形一个内角的________与它的对边相交,这个角顶点与交点之间的_____
顶点
垂足
线段
中点
线段
平分线
线段
A
B
D
C
A
B
D
C
∵ AD是△ABC的中线
∴ BD=CD= BC
∵AD是△ABC的高线
∴AD⊥BC
∠ADB=∠ADC=90°
∵.AD是∠BAC的平分线
∴ ∠1=∠2= ∠BAC
A
B
D
C
1
2
A
B
D
C
A
B
D
C
A
B
D
C
1
2
重心
第九章 三角形
9.3 三角形的角平分线、中线和高
学习目标
1.理解三角形的角平分线、中线、高线的概念.
2.会画出已知三角形的角平分线、中线和高.
3.掌握“三线”的性质,并能应用进行计算.
学习重难点
掌握“三线”的性质,并能应用进行计算.
掌握“三线”的性质,并能应用进行计算.
难点
重点
复习导入
上节课我们学习三角形按角分为哪几类?
1.锐角三角形;2.直角三角形;3.钝角三角形。
新知引入
知识点1 三角形的角平分线
1.复习用量角器或折纸的办法画出或折出一个角的平分线。
角平分线的定义及画法:
从一个角的顶点引出的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线。
A
B
C
D
定义:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫三角形的角平分线。
角平分线的符号语言:
∵ AD是△ABC的角平分线
∴∠BAD=∠CAD= ∠BAC
2.什么是三角形的角平分线?
3.想一想,锐角三角形、直角三角形、钝角三角形分别有几条角平分线?画出它们的角平分线,观察它们有什么特点
锐角三角形
钝角三角形
直角三角形
①三角形的角平分线是一条线段,而角平分线是一条射线。
②任何三角形有三条角平分线,并且都在三角形的内部交于一点。
例题示范
要知道DO 是不是△DEF 的角平
分线,只需要知道∠EDO 与
∠FDO 是否相等.若相等,根
据三角形的角平分线的定义即
可判定.
例1
如图,△ABC 中,AD 是△ABC 的角平分线,DE∥AC,DF∥AB,EF 交AD 于点O,请问DO 是△DEF 的角平分线吗?说明理由.
导引:
DO 是△DEF 的角平分线.理由如下:
因为AD是△ABC 的角平分线,
所以∠DAB=∠DAC (角平分线定义).
因为DE∥AC,DF∥AB,
所以∠DAC=∠ADE,∠DAB=∠ADF (两直线平行,内错角相等),所以∠ADE=∠ADF (等量代换),
所以DO 是△DEF 的角平分线.
解:
总结
本例在解题过程中,先利用角平分线的定义,得出相等的角,再结合相关条件(如平行等)推出新的一组相等的角,最后由角平分线的定义说明角平分线,它经历了定义→条件→定义的过程,这就是定义法.
知识点2 三角形的中线
1.复习线段中点的定义:
把一条线段分成两条相等的线段的点。
A
B
C
D
.
定义:在三角形中,连接一个顶点和它的对边中点的线段叫做这个三角形的中线。
三角形中线的符号语言:
∵AD是△ABC的中线
∴BD=CD=
1
2
BC
2.什么是三角形的中线?
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
3.想一想,锐角三角形、直角三角形、钝角三角形分别有几条中线?画出它们的中线,观察它们有什么特点
①三角形的中线是一条线段。
②任何三角形有三条中线,并且都在三角形的内部交于一点,这个交点叫做这个三角形的重心。
4.用薄厚均匀的硬纸板裁出一个三角形,画出这个三角形的三条中线,在它们的交点处钻一个小孔,通过小孔系一条线将三角形硬纸板吊起,三角形硬纸板处于什么状态?这种现象说明了什么?
三角形硬纸板处于平衡状态,这种现象说明了重心能使物体保持平衡。
例2
张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.
根据等底同高的三角形的面积相
等,要等分三角形的面积,只需
要作出一条边上的中线即可.
导引:
解:
根据要求,平分田地的直线必须经过三角形的顶点.画△ABC 的中线AD (如图),则AD 就把△ABC 的面积平分成两份.这是因为AD 是△ABC 的中线,所以BD=DC.过点A 作AE⊥BC 于点E.在△ABD 和△ACD 中,因为BD,CD 边上的高都是AE,所以由三角形的面积计算公式,知△ABD 和△ACD 的面积相等,因此,要把△ABC 平分成两个三角形,只需画中线AD 即可,这是一种平分方法.(本题答案不唯一,作AB,AC 边上的中线也可以)
总结
(1)三角形的任意一条中线都能把三角形分成面积相
等的两部分,即等底同高的三角形面积相等;
(2)拓展:在两个三角形中:底、高、面积这三个量,
如果有其中的两个量相等,那么第三个量也相等.
知识点3 三角形的高
1. 复习“过一点作已知直线的垂线”:
A
B
C
定义:三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,简称三角形的高。
D
三角形高的符号语言:
∵AD是△ABC的高
∴AD⊥BC或∠ADC=∠ADB=90°
2.什么是三角形的高线?
3.想一想,锐角三角形、直角三角形、钝角三角形分别有几条高线?画出它们的高线,观察它们有什么特点
①三角形的高是一条线段。
②任何三角形有三条高,三条高(或高的延长线)相交于一点。可分为锐角三角形(内部),直角三角形(直角顶点),钝角三角形(外部)。
画出图中△ABC 的三条高.(要标明字母,不写画法)
例3
导引:
“作一边上的高”,即可看作“过一点(这边所对角的顶点)作已知直线(这边所在的直线)的垂线.”按照“过一点作已知直线的垂线”进行作图,顶点与垂足之间的线段即为该边上的高;需注意AB,BC 边上的高在三角形的外部,作高时先延长AB 与CB.
解:
如图所示.
总结
(1)作三角形的高时,找准顶点和对边是关键,作高的步骤就是“过一点作已知直线的垂线”的步骤:
一靠(三角尺的一条直角边靠在要作高的边上)、
二找(移动三角尺使另一条直角边通过要作高的顶点)、三画线(画垂线段),如图.
(2)注意:高是线段,垂线是直线.
随堂练习
1、下列各组图形中,哪一组图形中AD是△ABC的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A.
B.
C.
D.
2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形
B
D
3、如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35 cm,BC=11 cm,且△ABD与△ACD的周长之差为3 cm,求AB与AC的长.
A
C
D
B
解:∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
又∵△ABD与△ACD的周长之差为3cm,
∴AB-AC=3,
∴AB=13.5cm,AC=10.5cm.
拓展提升
能把三角形平分成两个面积相等的三角形的线段是( )
A.三角形的中线
B.三角形的高
C.三角形的角平分线
D.以上三种情况都正确
A
1
如图,AD 是∠CAB 的平分线,DE∥AB,DF∥AC,EF 交AD 于点O.
请问:
(1)DO 是∠EDF 的平分线吗?
如果是,请给予证明;
如果不是,请说明理由.
(2)若将“DO 是∠EDF 的平分线”与“AD 是∠CAB 的平分线”,“DE∥AB ”,“DF∥AC ”三个条件中的任一条件交换,所得说法正确吗?若正确,请选择一个说明理由.
2
(1)DO 是∠EDF 的平分线.
证明如下:∵AD是∠CAB 的平分线,
∴∠EAD=∠FAD.
∵DE∥AB,DF∥AC,
∴∠EDA=∠FAD,∠FDA=∠EAD.
∴∠EDA=∠FDA.
∴DO 是∠EDF 的平分线.
解:
(2)与三个条件中的任一条件交换,所得说法都正确.
若和“DE∥AB ”交换.
理由如下:∵DF∥AC,∴∠FDA=∠EAD.
∵AD 是∠CAB 的平分线,
∴∠EAD=∠FAD.∴∠FAD=∠FDA.
∵DO 是∠EDF 的平分线,
∴∠EDA=∠FDA.∴∠EDA=∠FAD.
∴DE∥AB.
(答案不唯一)
如图,在△ABC 中,AD⊥BC,BE⊥AC,垂足分别
为D,E,若BC=10,AC=8,BE= ,求AD 的长.
4
∵AD⊥BC,BE⊥AC,
∴S△ABC= ·BC·AD= ·AC·BE.
∴BC ·AD=AC ·BE.
又∵BC=10,AC=8,BE= ,
∴10AD=8× .
∴AD=6.8.
解:
归纳小结
三角形的 重要线段 概念 图示 表述方式
三角形 的高线 从三角形的一个顶点向它的对边所在的直线作垂线,_____和_____之间的 _____
三角形 的中线 三角形中,连结一个顶点和它对边 ____的 ____,三条中线的交点叫做_____
三角形的 角平分线 三角形一个内角的________与它的对边相交,这个角顶点与交点之间的_____
顶点
垂足
线段
中点
线段
平分线
线段
A
B
D
C
A
B
D
C
∵ AD是△ABC的中线
∴ BD=CD= BC
∵AD是△ABC的高线
∴AD⊥BC
∠ADB=∠ADC=90°
∵.AD是∠BAC的平分线
∴ ∠1=∠2= ∠BAC
A
B
D
C
1
2
A
B
D
C
A
B
D
C
A
B
D
C
1
2
重心
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
