人教版六年级数学下册第五单元《数学广角——鸽巢问题》5.2 鸽巢问题(2)(课件)(共31张PPT)
文档属性
| 名称 | 人教版六年级数学下册第五单元《数学广角——鸽巢问题》5.2 鸽巢问题(2)(课件)(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 16:34:48 | ||
图片预览








文档简介
(共31张PPT)
第 1 课时 | 鸽巢问题2
第五单元 数学广角——鸽巢问题
任 课 教 师 | X X X
人教版六年级数学下册
知识无涯,进步无界!
小学数学小班化“1+1”教学模式
新理念
新模式
新课标
新征程
教 学 重 点
在了解简单的“鸽巢问题”的基础上,使学生会用此原理解决简单的实际问题。
1
教 学 难 点
能进一步理解“抽屉原理”,运用“抽屉原理”进行逆向思维。
2
重点难点
知
界
无
识
知识无涯,进步无界!
亲爱的同学们,请开始
你的读学内容,把你的
读学困惑记录下来吧!
预
习
读
学
内
容
课本第69页
个人读学困惑 记录表 问题 困惑内容
问题1
问题2
问题3
问题4
知识无涯,进步无界!
预
学
读
习
小组读学困惑 汇总表 困惑学生姓名 问题 困惑内容
问题1
问题2
问题3
问题4
问题5
知识无涯,进步无界!
团
学
互
队
填一填。
(1)把5支笔放进2个文具盒,不管怎么放,总有一个文具盒里至少有( )支笔。
(2)李老师参加射击比赛,射了3发(都是整数环),成绩是 25 环,他至少有一发的成绩不低于( )环。
3
9
想一想,为什么会出现这种情况呢?
把多于kn个物体任意放进n个鸽巢里(n≥2,n,k是正整数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
这节课我们来学习鸽巢问题的应用。
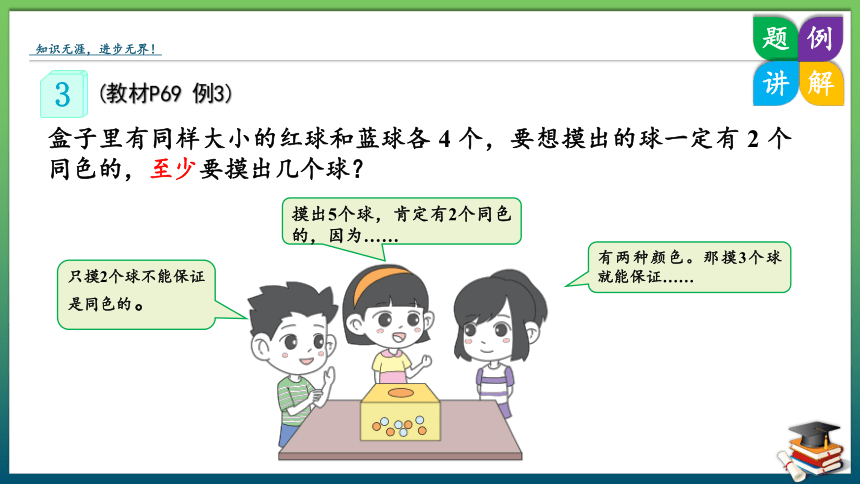
(教材P69 例3)
3
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为……
有两种颜色。那摸3个球就能保证……
只摸2个球不能保证是同色的。
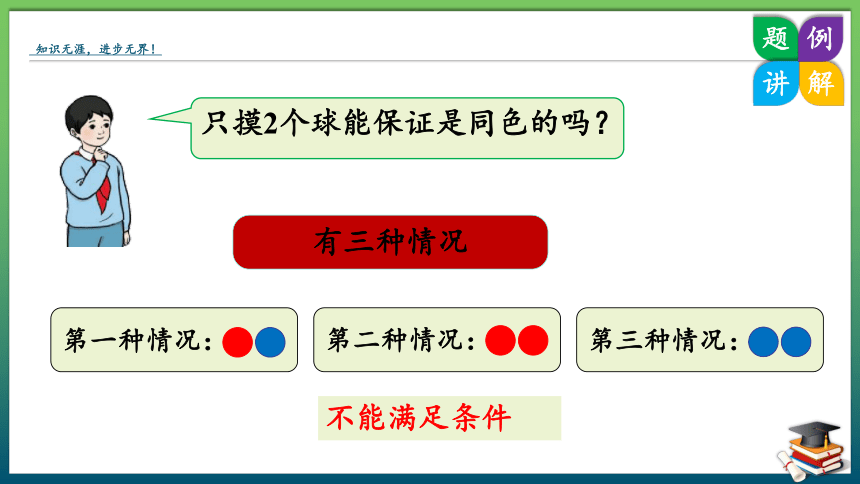
只摸2个球能保证是同色的吗?
有三种情况
第一种情况:
第二种情况:
第三种情况:
不能满足条件
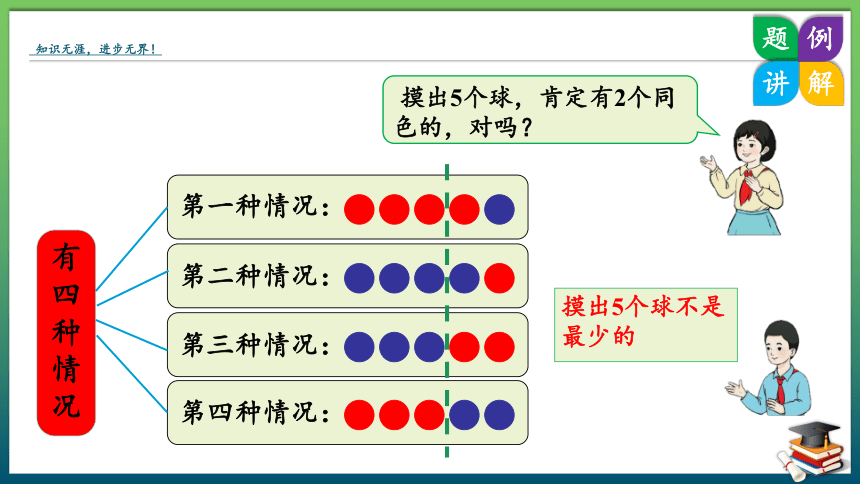
摸出5个球,肯定有2个同色的,对吗?
第一种情况:
第二种情况:
第三种情况:
第四种情况:
有四种情况
摸出5个球不是最少的
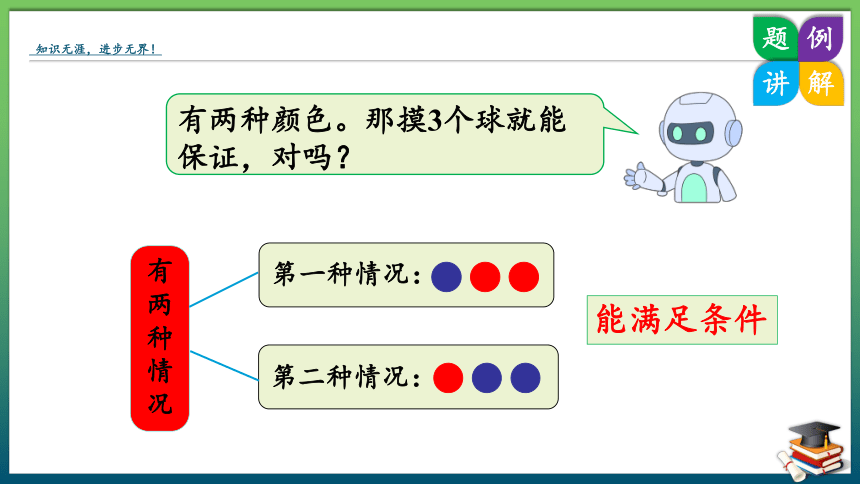
有两种颜色。那摸3个球就能保证,对吗?
第一种情况:
第二种情况:
有两种情况
能满足条件
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
至少要摸出3个球。
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄利克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄利克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
动脑想一想,用“鸽巢原理”解决实际问题的一般步骤。
(1)分析题意,把实际问题转化成“鸽巢问题”,即弄清“鸽巢是什么,有几个鸽巢”和分放的物体的总个数;
(2)设计“鸽巢”的具体形式,即“鸽巢原理”;
(3)运用鸽巢原理,得出在某个“鸽巢”中至少分放的物体的个数,从而求出实际问题的解。
1.向东小学六年级共有367名学生,其中六(2)班有37名学生。(教材P69 做一做 第1题)
六年级里至少有2个人在同一天过生日。
六(2)班中至少有4个人在同一个月过生日。
他说得对吗?为什么?
1.向东小学六年级共有367名学生,其中六(2)班有37名学生。(教材P69做一做 第1题)
六年级里至少有两人在同一天过生日。
367÷365=1······2
1+1=2
通过本节课的学习,我们在了解简单的“鸽巢问题”的基础上,会用此原理解决简单的实际问题。进一步理解“抽屉原理”,运用“抽屉原理”进行逆向思维。
(1)分析题意,把实际问题转化成“鸽巢问题”,即弄清“鸽巢是什么,有几个鸽巢”和分放的物体的总个数;
(2)设计“鸽巢”的具体形式,即“鸽巢原理”;
(3)运用鸽巢原理,得出在某个“鸽巢”中至少分放的物体的个数,从而求出实际问题的解。
用“鸽巢原理”解决实际问题的一般步骤
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
乐学
善思
本课结束 感谢聆听!
第 1 课时 | 鸽巢问题2
第五单元 数学广角——鸽巢问题
任 课 教 师 | X X X
人教版六年级数学下册
知识无涯,进步无界!
小学数学小班化“1+1”教学模式
新理念
新模式
新课标
新征程
教 学 重 点
在了解简单的“鸽巢问题”的基础上,使学生会用此原理解决简单的实际问题。
1
教 学 难 点
能进一步理解“抽屉原理”,运用“抽屉原理”进行逆向思维。
2
重点难点
知
界
无
识
知识无涯,进步无界!
亲爱的同学们,请开始
你的读学内容,把你的
读学困惑记录下来吧!
预
习
读
学
内
容
课本第69页
个人读学困惑 记录表 问题 困惑内容
问题1
问题2
问题3
问题4
知识无涯,进步无界!
预
学
读
习
小组读学困惑 汇总表 困惑学生姓名 问题 困惑内容
问题1
问题2
问题3
问题4
问题5
知识无涯,进步无界!
团
学
互
队
填一填。
(1)把5支笔放进2个文具盒,不管怎么放,总有一个文具盒里至少有( )支笔。
(2)李老师参加射击比赛,射了3发(都是整数环),成绩是 25 环,他至少有一发的成绩不低于( )环。
3
9
想一想,为什么会出现这种情况呢?
把多于kn个物体任意放进n个鸽巢里(n≥2,n,k是正整数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
这节课我们来学习鸽巢问题的应用。
(教材P69 例3)
3
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为……
有两种颜色。那摸3个球就能保证……
只摸2个球不能保证是同色的。
只摸2个球能保证是同色的吗?
有三种情况
第一种情况:
第二种情况:
第三种情况:
不能满足条件
摸出5个球,肯定有2个同色的,对吗?
第一种情况:
第二种情况:
第三种情况:
第四种情况:
有四种情况
摸出5个球不是最少的
有两种颜色。那摸3个球就能保证,对吗?
第一种情况:
第二种情况:
有两种情况
能满足条件
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
至少要摸出3个球。
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄利克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄利克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
动脑想一想,用“鸽巢原理”解决实际问题的一般步骤。
(1)分析题意,把实际问题转化成“鸽巢问题”,即弄清“鸽巢是什么,有几个鸽巢”和分放的物体的总个数;
(2)设计“鸽巢”的具体形式,即“鸽巢原理”;
(3)运用鸽巢原理,得出在某个“鸽巢”中至少分放的物体的个数,从而求出实际问题的解。
1.向东小学六年级共有367名学生,其中六(2)班有37名学生。(教材P69 做一做 第1题)
六年级里至少有2个人在同一天过生日。
六(2)班中至少有4个人在同一个月过生日。
他说得对吗?为什么?
1.向东小学六年级共有367名学生,其中六(2)班有37名学生。(教材P69做一做 第1题)
六年级里至少有两人在同一天过生日。
367÷365=1······2
1+1=2
通过本节课的学习,我们在了解简单的“鸽巢问题”的基础上,会用此原理解决简单的实际问题。进一步理解“抽屉原理”,运用“抽屉原理”进行逆向思维。
(1)分析题意,把实际问题转化成“鸽巢问题”,即弄清“鸽巢是什么,有几个鸽巢”和分放的物体的总个数;
(2)设计“鸽巢”的具体形式,即“鸽巢原理”;
(3)运用鸽巢原理,得出在某个“鸽巢”中至少分放的物体的个数,从而求出实际问题的解。
用“鸽巢原理”解决实际问题的一般步骤
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
乐学
善思
本课结束 感谢聆听!
