苏教版六年级数学下册4.2比例的意义(课件)(共18张PPT)
文档属性
| 名称 | 苏教版六年级数学下册4.2比例的意义(课件)(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 18:46:22 | ||
图片预览





文档简介
(共18张PPT)
苏教版小学数学六年级下册
4.2 比例的意义
学习目标
1、理解比例的意义,认识比例各部分的名称。
2、经历探索比例的意义的过程,并能运用比例的
意义,判断两个比能否组成比例,会组比例。
3、培养学生自主参与的意识、主动探究的精神;
发展学生思维,体验到学习数学的愉悦。
学习重点:理解比例的意义。
学习难点:应用比例的意义判断两个比能否组成比例。
一、情境引入:
复习导入:
1、化简比:
36:8=( );3.2:1.2=( );
2、求比值:
9:3=( ); 3.6:9=( );
=( )。
=( )。
3、放大或缩小后的图形与原图形相比,
为什么形状不会发生改变?
9:2
8:3
3:1
3:1
2:5
3:4
探究新知
1、认识比例:
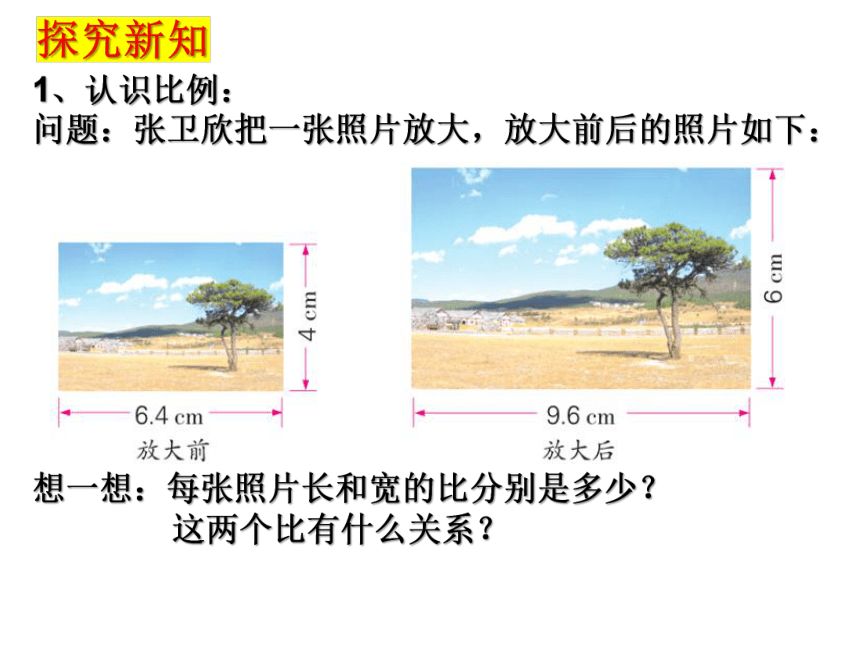
问题:张卫欣把一张照片放大,放大前后的照片如下:
想一想:每张照片长和宽的比分别是多少?
这两个比有什么关系?
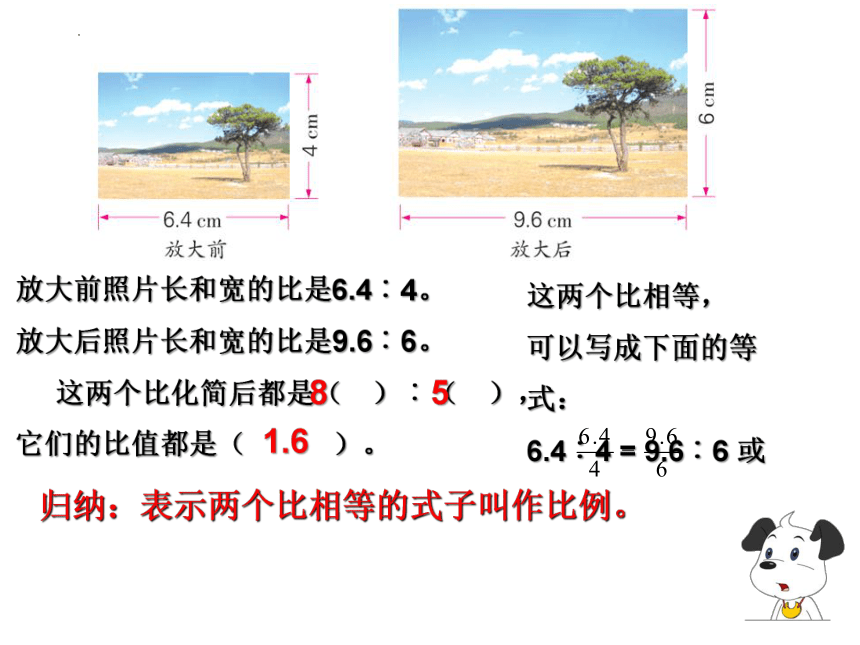
放大前照片长和宽的比是6.4︰4。
放大后照片长和宽的比是9.6︰6。
这两个比化简后都是( )︰( ),
它们的比值都是( )。
这两个比相等,
可以写成下面的等式:
6.4︰4 = 9.6︰6 或
8 5
1.6
归纳:表示两个比相等的式子叫作比例。
议一议:
分别写出照片放大后与放大前长的比和宽的比,这两个比也能组成比例吗?
照片放大后与放大前长的比为6.4:9.6=( ),
照片放大后与放大前宽的比4:6=( )。
这两个比( )组成比例。
(填“能”或“不能”)
2:3
2:3
能
练一练:
1、下列各组两个比,其中可以组成比例的
一共有( )组。
(1) 10︰12 和 25︰30 ;(2) 2︰8 和 9︰27;(3) (4)
A、一 B、二 C、三 D、四
2、一辆汽车上午3小时行驶了270km,
下午5小时行驶了450km,
(1)上午行驶的路程和时间的比是( );
(2)下午行驶的路程和时间的比是( );
(3)这两个比能组成比例吗?为什么?
二、例题讲解:
例1、 如图,
(1)参加跳绳的男、女生人数的比是多少?
参加捉迷藏的男、女生人数的比是多少?
它们能否组成比例?
(2)参加跳绳和捉迷藏男生人数的比与女生人数
的比能组成比例吗?如果能,把比例写出来。
例2、一个人的身高1.5米,一棵树的高度是3.5米,在同一时刻,同一地点阳光下,该人的影子影长1.2米,该树的影长是2.8米。分别求出人的身高和人的影长比,树的高度与树的影长比,这两组比能组成比例吗?
三、基础强化:
1、判断题:
(1)有两个比组成的式子叫比例。 ( )
(2)如果两个比可以组成比例,
这两个比的比值一定相等。 ( )
(3)0.1:0.3与2:6能组成比例。 ( )
(4)组成比例的两个比一定是最简比。( )
2、下面的式子中,( )是比例。
A、2.5︰1.5 > 20︰15 B、2×6=3+9
C、2.4︰3 =0.8 D、48︰8= 12︰2
A、6︰5 B、3:20
3、下面的比中,不能与 组成的比例的是( )
C、 D、0.9︰6
4、用20以内4个合数组成一个比例
( )。
5、两个比的比值都是0.75,且一个比的前项
与另一个比的后项都是6,把这两个比
组成比例是( )。
四、拓展提高:
6、如果数x与2、4、6能组成比例,
则x的值为( )。
7、有两个比,它们的比值都是 ,第一个比的前项和后一个比的后项都是12,这两个比组成的比例是( ) 。
五、总结反思:
1、比例的意义:
表示两个比相等的式子。
2、如何判断两个比能否成比例?
两个比化简后,如果两个比的比值相等,
这两个比就能组成比例,否则,就不能组成比例。
六、随堂检测:
1、下面哪组中的两个比可以组成比例
(1)6:10和9:15 (2)20:5和1:4
(3) 和6:4 (4)0.6:0.2和
2、0.8和6的比等于x和15的比,求x的值。
3、用6、7、18和21四个数组成不同的比例。
(写4个不同的比例)
4、张老师为了布置教室,制作了三幅图画。
(1)写出每幅图画的长与宽的比,并算出比值。
(2)选择其中两个合适的比组成比例。
苏教版小学数学六年级下册
4.2 比例的意义
学习目标
1、理解比例的意义,认识比例各部分的名称。
2、经历探索比例的意义的过程,并能运用比例的
意义,判断两个比能否组成比例,会组比例。
3、培养学生自主参与的意识、主动探究的精神;
发展学生思维,体验到学习数学的愉悦。
学习重点:理解比例的意义。
学习难点:应用比例的意义判断两个比能否组成比例。
一、情境引入:
复习导入:
1、化简比:
36:8=( );3.2:1.2=( );
2、求比值:
9:3=( ); 3.6:9=( );
=( )。
=( )。
3、放大或缩小后的图形与原图形相比,
为什么形状不会发生改变?
9:2
8:3
3:1
3:1
2:5
3:4
探究新知
1、认识比例:
问题:张卫欣把一张照片放大,放大前后的照片如下:
想一想:每张照片长和宽的比分别是多少?
这两个比有什么关系?
放大前照片长和宽的比是6.4︰4。
放大后照片长和宽的比是9.6︰6。
这两个比化简后都是( )︰( ),
它们的比值都是( )。
这两个比相等,
可以写成下面的等式:
6.4︰4 = 9.6︰6 或
8 5
1.6
归纳:表示两个比相等的式子叫作比例。
议一议:
分别写出照片放大后与放大前长的比和宽的比,这两个比也能组成比例吗?
照片放大后与放大前长的比为6.4:9.6=( ),
照片放大后与放大前宽的比4:6=( )。
这两个比( )组成比例。
(填“能”或“不能”)
2:3
2:3
能
练一练:
1、下列各组两个比,其中可以组成比例的
一共有( )组。
(1) 10︰12 和 25︰30 ;(2) 2︰8 和 9︰27;(3) (4)
A、一 B、二 C、三 D、四
2、一辆汽车上午3小时行驶了270km,
下午5小时行驶了450km,
(1)上午行驶的路程和时间的比是( );
(2)下午行驶的路程和时间的比是( );
(3)这两个比能组成比例吗?为什么?
二、例题讲解:
例1、 如图,
(1)参加跳绳的男、女生人数的比是多少?
参加捉迷藏的男、女生人数的比是多少?
它们能否组成比例?
(2)参加跳绳和捉迷藏男生人数的比与女生人数
的比能组成比例吗?如果能,把比例写出来。
例2、一个人的身高1.5米,一棵树的高度是3.5米,在同一时刻,同一地点阳光下,该人的影子影长1.2米,该树的影长是2.8米。分别求出人的身高和人的影长比,树的高度与树的影长比,这两组比能组成比例吗?
三、基础强化:
1、判断题:
(1)有两个比组成的式子叫比例。 ( )
(2)如果两个比可以组成比例,
这两个比的比值一定相等。 ( )
(3)0.1:0.3与2:6能组成比例。 ( )
(4)组成比例的两个比一定是最简比。( )
2、下面的式子中,( )是比例。
A、2.5︰1.5 > 20︰15 B、2×6=3+9
C、2.4︰3 =0.8 D、48︰8= 12︰2
A、6︰5 B、3:20
3、下面的比中,不能与 组成的比例的是( )
C、 D、0.9︰6
4、用20以内4个合数组成一个比例
( )。
5、两个比的比值都是0.75,且一个比的前项
与另一个比的后项都是6,把这两个比
组成比例是( )。
四、拓展提高:
6、如果数x与2、4、6能组成比例,
则x的值为( )。
7、有两个比,它们的比值都是 ,第一个比的前项和后一个比的后项都是12,这两个比组成的比例是( ) 。
五、总结反思:
1、比例的意义:
表示两个比相等的式子。
2、如何判断两个比能否成比例?
两个比化简后,如果两个比的比值相等,
这两个比就能组成比例,否则,就不能组成比例。
六、随堂检测:
1、下面哪组中的两个比可以组成比例
(1)6:10和9:15 (2)20:5和1:4
(3) 和6:4 (4)0.6:0.2和
2、0.8和6的比等于x和15的比,求x的值。
3、用6、7、18和21四个数组成不同的比例。
(写4个不同的比例)
4、张老师为了布置教室,制作了三幅图画。
(1)写出每幅图画的长与宽的比,并算出比值。
(2)选择其中两个合适的比组成比例。
