初中数学人教版八年级下册 第十八章 平行四边形 小结教学设计(表格式)
文档属性
| 名称 | 初中数学人教版八年级下册 第十八章 平行四边形 小结教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 311.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 平行四边形的整理复习
教学目标
1.进一步理解平行四边形、矩形、菱形、正方形的概念及其相互联系。 2.掌握平行四边形、矩形、菱形、正方形的性质和判定,会进行结构化整理。 3.掌握图形研究的基本思路,并会研究其他平面图形。
教学内容
教学重点: 1.会归纳出各种平行四边形的研究内容、研究步骤和研究方法。
2.梳理平行四边形的知识结构体系,会选择适当的知识进行推理计算,并解决问题。
教学难点: 1.应用特殊四边形的定义、性质、判定相关知识解决问题。
2.利用特殊四边形研究思路,对其他平面图形进行研究。
教学过程
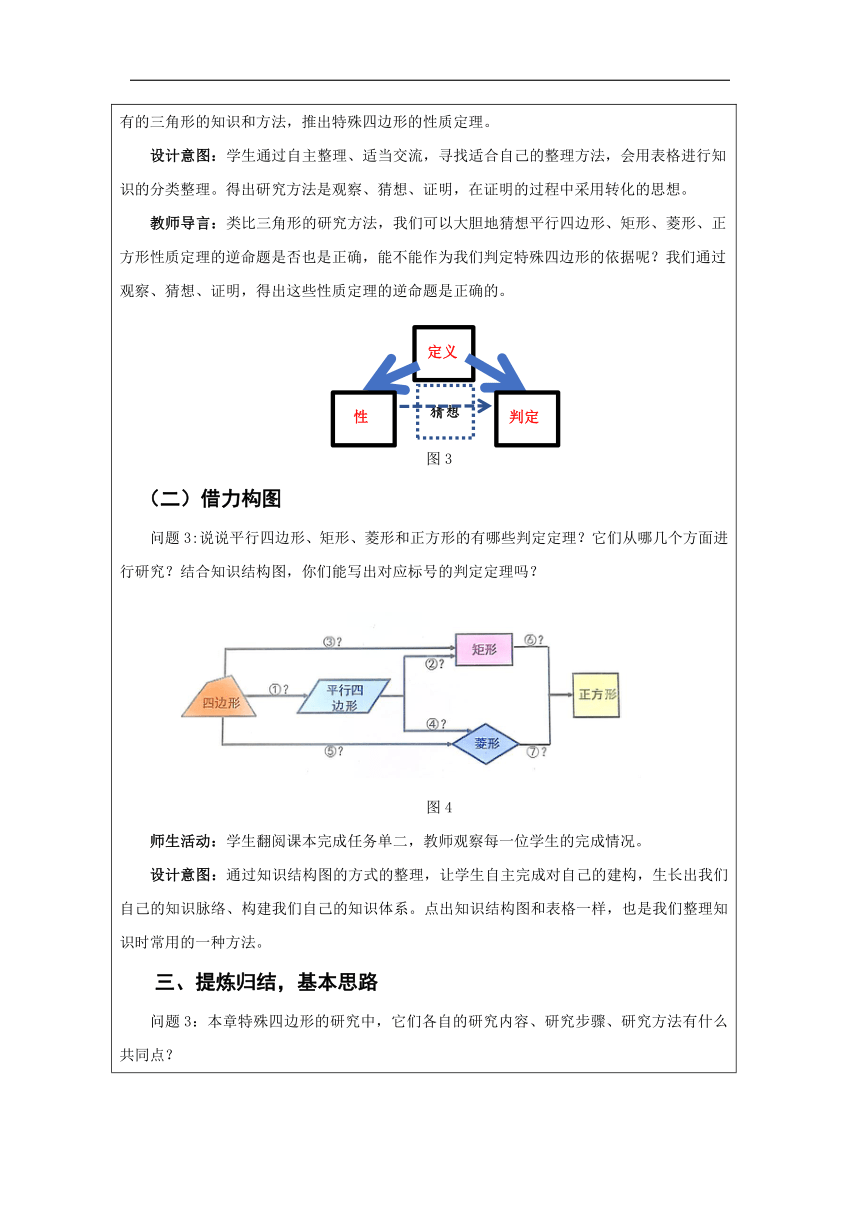
一、回溯知识,理清脉络 教师引言:本章我们在四边形的基础上,进一步学习了一些特殊的四边形,它们分别是平行四边形、矩形、菱形、正方形。 问题1:说一说本章是按照什么顺序学习这些特殊的四边形? 图1 师生活动:学生快速再读课本,理清教材编排,完成【随课快题1】,回溯特殊四边形的学习过程。教师引导学生如何速读教材内容。师生共同讨论、交流得出,本章是按照“四边形——平行四边形——矩形、菱形——正方形”这个次序来学的。 设计意图:通过对图形不断殊化,不断进行类比展示,让学生得出从一般到特殊、类比两种基本的数学思想。 追问1: 请说说这些四边形之间的从属关系 图2 师生活动:教师引导学生进行从属关系的思考,完成【随课快题2】,并展示正确的结果。 设计意图:借助集合,进一步理清四边形、平行四边形、矩形、菱形、正方形之间的界限,使学生能更清晰地了解它们的定义。 整理优化 (一)借力表格 问题2:说说平行四边形、矩形、菱形和正方形的性质?它们从哪几个方面进行研究?能用表格归纳吗? 表1 师生活动:学生自主对照课本自主整理特殊四边形的性质,教师引导学生用表格进行知识的归纳整理。在图形研究过程中,我们先定义,再性质,点出性质定理也是我们进一步认识、理解这些特殊四边形的关键。而这些性质定理得出都经历了观察、猜想、证明,利用已有的三角形的知识和方法,推出特殊四边形的性质定理。 设计意图:学生通过自主整理、适当交流,寻找适合自己的整理方法,会用表格进行知识的分类整理。得出研究方法是观察、猜想、证明,在证明的过程中采用转化的思想。 教师导言:类比三角形的研究方法,我们可以大胆地猜想平行四边形、矩形、菱形、正方形性质定理的逆命题是否也是正确,能不能作为我们判定特殊四边形的依据呢?我们通过观察、猜想、证明,得出这些性质定理的逆命题是正确的。 图3 (二)借力构图 问题3:说说平行四边形、矩形、菱形和正方形的有哪些判定定理?它们从哪几个方面进行研究?结合知识结构图,你们能写出对应标号的判定定理吗? 图4 师生活动:学生翻阅课本完成任务单二,教师观察每一位学生的完成情况。 设计意图:通过知识结构图的方式的整理,让学生自主完成对自己的建构,生长出我们自己的知识脉络、构建我们自己的知识体系。点出知识结构图和表格一样,也是我们整理知识时常用的一种方法。 提炼归结,基本思路 问题3:本章特殊四边形的研究中,它们各自的研究内容、研究步骤、研究方法有什么共同点? 图5 师生活动:通过学生回顾、教师提问等形式,分别从图形研究内容、步骤、方法古三个方面,总结研究几何图形的基本思路。 设计意图:通过对特殊四边形的研究思路的总结归纳,得到一般几何图形研究的基本思路。 四、应用知识,解决问题 例1(2021年玉环市期末卷)如图 , ABCD的对角线AC,BD相交于点O,E是BC的中点,BF//AC交OE的延长线于点F,连接CF. (1)求证:四边形BFCO是平行四边形; (2)当 ABCD是__菱形____时, BFCO是矩形; (3)当 ABCD是__矩形___时, BFCO是菱形; (填“矩形”、“菱形”或“正方形”) (1)证明:∵E是BC的中点 ∴BE=CE 图6 ∵BF//AC ∴∠EBF=ECO,∠EFB=∠EOC ∴△EFB≌△EOC(AAS) ∴EF=EO ∴四边形BFCO是平行四边形 师生活动:学生自主探究,学生代表起立讲解题思路,教师和其他学生倾听,判断学生解题是否正确,并让学生回溯解题过程,解题方法。 设计意图:通过本题解题,让学生选择合适的条件判定特殊四边形。在知识的应用过程中,让学生体会平行四边形的许多题目,往往可以转化为三角形的知识和方法来解决。其中(1)从条件出发推出结论,这是我们常见的一种证明思路叫顺推。(2)和(3)从结论出发,从而达到解决问题的目的,这种方法叫逆推。 例2 定义:有一组对边平行,另一组对边不平行的四边形叫做梯形,其中两条腰相等的梯形叫等腰梯形. 结合本章学到的知识,你打算如何研究等腰梯形? 结合图形,说说等腰梯形的性质?并选择其中一个性质,试着去证明它。 (3)结合图形,说说等腰梯形的判定?并选择其中一个性质,试着去证明它。 解:(1) 研究内容:边、角、对角线的特征 研究步骤:分别先定义、后性质、判定 研究方法:类比特殊平行四边形 观察、猜想、证明 (2)我们对等腰梯形的边、角、对角线的特征进研究发现: 图7 边:两腰相等 角:同一底上的两个底角相等 对角线:对角线相等 我们选“同一底上的两个底角相等”对其进行证明。 已知:四边形ABCD是等腰梯形 求证:∠B=∠C 证明:过D作ED//AB,交BC于E ∵四边形ABCD是等腰梯形 ∴AD//BC ,AB=DC ∴四边形ABED是平行四边形 ∴DE=AB, ∠B=∠1 图8 ∴DE=DC ∴ ∠C=∠1 ∴∠B=∠C 边:两腰相等的梯形是等腰梯形 角:同一底上的两个底角相等的梯形是等腰梯形 对角线:对角线相等的梯形是等腰梯形 我们选择“对角线相等的梯形是等腰梯形”来证明。 已知:AD//BC,∠B=∠C 求证:梯形ABCD是等腰梯形 证明:过D作DE//AC,交BC延长线于E ∵AD//BE ∴四边形ACED是平行四边形 ∴AC=DE,∠E=∠2 ∵AC=BD ∴BE=DE ∴∠1=∠E ∴∠1=∠2 ∴△BCD≌△CBA(SAS) 图9 ∴AB=CD ∴梯形ABCD是等腰梯形 师生活动:学生自主探究,学生代表起立讲解题思路,教师和其他学生倾听,判断学生解题是否正确,并让学生回溯解题过程,解题方法。 设计意图:本题的证明过程中,我们找到一个中间条件,然后已知和需要证明的结论分别往中间凑,最终达到解决问题的方法,这种解题的方法叫两头凑。面对等腰梯形的证明问题,我们的解题思路始终是将梯形问题转化为平行四边形或三角形的知识和方法来研究,这种化陌生为已知的思想也是我们认识世界、解决问题一个种很重要的方法。 课堂小结 图10 师生活动:学生谈收获、教师结合图10作小结:我们按照从一般到特殊、类比、转化的研究方法,将四边形不断进行特殊化,分别研究平行四边形、矩形、菱形、正方形,其研究内容是对这些特殊四边形的边、角、对角线特征的研究,其研究步骤按先定义、后性质、判定,其中通过性质定理的逆命题猜想得到判定定理。通过对特殊四边形的研究,我们得到了一般图形研究的基本思想。通过类比,我们用这种基本思种进行迁移应用,将四边形特殊成梯形这样一个新的方向,开展了等腰梯形的研究。 伟大的数学家毕达哥拉斯曾经说过,在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。数学学习既要重视知识整理内化、又要注重研究思想的总结,它需要我们不断地探索,不断地去发现。 我们对四边形的研究,还没有结束,大家课后可以用我们学到的基本思路继续探索研究直角梯形的定义、性质、判定。 设计意图:在完成本堂学习内容和学生一起作好小结的同时,我们引导学生继续研究直角梯形,使四边形的研究更加完整。
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 平行四边形的整理复习
教学目标
1.进一步理解平行四边形、矩形、菱形、正方形的概念及其相互联系。 2.掌握平行四边形、矩形、菱形、正方形的性质和判定,会进行结构化整理。 3.掌握图形研究的基本思路,并会研究其他平面图形。
教学内容
教学重点: 1.会归纳出各种平行四边形的研究内容、研究步骤和研究方法。
2.梳理平行四边形的知识结构体系,会选择适当的知识进行推理计算,并解决问题。
教学难点: 1.应用特殊四边形的定义、性质、判定相关知识解决问题。
2.利用特殊四边形研究思路,对其他平面图形进行研究。
教学过程
一、回溯知识,理清脉络 教师引言:本章我们在四边形的基础上,进一步学习了一些特殊的四边形,它们分别是平行四边形、矩形、菱形、正方形。 问题1:说一说本章是按照什么顺序学习这些特殊的四边形? 图1 师生活动:学生快速再读课本,理清教材编排,完成【随课快题1】,回溯特殊四边形的学习过程。教师引导学生如何速读教材内容。师生共同讨论、交流得出,本章是按照“四边形——平行四边形——矩形、菱形——正方形”这个次序来学的。 设计意图:通过对图形不断殊化,不断进行类比展示,让学生得出从一般到特殊、类比两种基本的数学思想。 追问1: 请说说这些四边形之间的从属关系 图2 师生活动:教师引导学生进行从属关系的思考,完成【随课快题2】,并展示正确的结果。 设计意图:借助集合,进一步理清四边形、平行四边形、矩形、菱形、正方形之间的界限,使学生能更清晰地了解它们的定义。 整理优化 (一)借力表格 问题2:说说平行四边形、矩形、菱形和正方形的性质?它们从哪几个方面进行研究?能用表格归纳吗? 表1 师生活动:学生自主对照课本自主整理特殊四边形的性质,教师引导学生用表格进行知识的归纳整理。在图形研究过程中,我们先定义,再性质,点出性质定理也是我们进一步认识、理解这些特殊四边形的关键。而这些性质定理得出都经历了观察、猜想、证明,利用已有的三角形的知识和方法,推出特殊四边形的性质定理。 设计意图:学生通过自主整理、适当交流,寻找适合自己的整理方法,会用表格进行知识的分类整理。得出研究方法是观察、猜想、证明,在证明的过程中采用转化的思想。 教师导言:类比三角形的研究方法,我们可以大胆地猜想平行四边形、矩形、菱形、正方形性质定理的逆命题是否也是正确,能不能作为我们判定特殊四边形的依据呢?我们通过观察、猜想、证明,得出这些性质定理的逆命题是正确的。 图3 (二)借力构图 问题3:说说平行四边形、矩形、菱形和正方形的有哪些判定定理?它们从哪几个方面进行研究?结合知识结构图,你们能写出对应标号的判定定理吗? 图4 师生活动:学生翻阅课本完成任务单二,教师观察每一位学生的完成情况。 设计意图:通过知识结构图的方式的整理,让学生自主完成对自己的建构,生长出我们自己的知识脉络、构建我们自己的知识体系。点出知识结构图和表格一样,也是我们整理知识时常用的一种方法。 提炼归结,基本思路 问题3:本章特殊四边形的研究中,它们各自的研究内容、研究步骤、研究方法有什么共同点? 图5 师生活动:通过学生回顾、教师提问等形式,分别从图形研究内容、步骤、方法古三个方面,总结研究几何图形的基本思路。 设计意图:通过对特殊四边形的研究思路的总结归纳,得到一般几何图形研究的基本思路。 四、应用知识,解决问题 例1(2021年玉环市期末卷)如图 , ABCD的对角线AC,BD相交于点O,E是BC的中点,BF//AC交OE的延长线于点F,连接CF. (1)求证:四边形BFCO是平行四边形; (2)当 ABCD是__菱形____时, BFCO是矩形; (3)当 ABCD是__矩形___时, BFCO是菱形; (填“矩形”、“菱形”或“正方形”) (1)证明:∵E是BC的中点 ∴BE=CE 图6 ∵BF//AC ∴∠EBF=ECO,∠EFB=∠EOC ∴△EFB≌△EOC(AAS) ∴EF=EO ∴四边形BFCO是平行四边形 师生活动:学生自主探究,学生代表起立讲解题思路,教师和其他学生倾听,判断学生解题是否正确,并让学生回溯解题过程,解题方法。 设计意图:通过本题解题,让学生选择合适的条件判定特殊四边形。在知识的应用过程中,让学生体会平行四边形的许多题目,往往可以转化为三角形的知识和方法来解决。其中(1)从条件出发推出结论,这是我们常见的一种证明思路叫顺推。(2)和(3)从结论出发,从而达到解决问题的目的,这种方法叫逆推。 例2 定义:有一组对边平行,另一组对边不平行的四边形叫做梯形,其中两条腰相等的梯形叫等腰梯形. 结合本章学到的知识,你打算如何研究等腰梯形? 结合图形,说说等腰梯形的性质?并选择其中一个性质,试着去证明它。 (3)结合图形,说说等腰梯形的判定?并选择其中一个性质,试着去证明它。 解:(1) 研究内容:边、角、对角线的特征 研究步骤:分别先定义、后性质、判定 研究方法:类比特殊平行四边形 观察、猜想、证明 (2)我们对等腰梯形的边、角、对角线的特征进研究发现: 图7 边:两腰相等 角:同一底上的两个底角相等 对角线:对角线相等 我们选“同一底上的两个底角相等”对其进行证明。 已知:四边形ABCD是等腰梯形 求证:∠B=∠C 证明:过D作ED//AB,交BC于E ∵四边形ABCD是等腰梯形 ∴AD//BC ,AB=DC ∴四边形ABED是平行四边形 ∴DE=AB, ∠B=∠1 图8 ∴DE=DC ∴ ∠C=∠1 ∴∠B=∠C 边:两腰相等的梯形是等腰梯形 角:同一底上的两个底角相等的梯形是等腰梯形 对角线:对角线相等的梯形是等腰梯形 我们选择“对角线相等的梯形是等腰梯形”来证明。 已知:AD//BC,∠B=∠C 求证:梯形ABCD是等腰梯形 证明:过D作DE//AC,交BC延长线于E ∵AD//BE ∴四边形ACED是平行四边形 ∴AC=DE,∠E=∠2 ∵AC=BD ∴BE=DE ∴∠1=∠E ∴∠1=∠2 ∴△BCD≌△CBA(SAS) 图9 ∴AB=CD ∴梯形ABCD是等腰梯形 师生活动:学生自主探究,学生代表起立讲解题思路,教师和其他学生倾听,判断学生解题是否正确,并让学生回溯解题过程,解题方法。 设计意图:本题的证明过程中,我们找到一个中间条件,然后已知和需要证明的结论分别往中间凑,最终达到解决问题的方法,这种解题的方法叫两头凑。面对等腰梯形的证明问题,我们的解题思路始终是将梯形问题转化为平行四边形或三角形的知识和方法来研究,这种化陌生为已知的思想也是我们认识世界、解决问题一个种很重要的方法。 课堂小结 图10 师生活动:学生谈收获、教师结合图10作小结:我们按照从一般到特殊、类比、转化的研究方法,将四边形不断进行特殊化,分别研究平行四边形、矩形、菱形、正方形,其研究内容是对这些特殊四边形的边、角、对角线特征的研究,其研究步骤按先定义、后性质、判定,其中通过性质定理的逆命题猜想得到判定定理。通过对特殊四边形的研究,我们得到了一般图形研究的基本思想。通过类比,我们用这种基本思种进行迁移应用,将四边形特殊成梯形这样一个新的方向,开展了等腰梯形的研究。 伟大的数学家毕达哥拉斯曾经说过,在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。数学学习既要重视知识整理内化、又要注重研究思想的总结,它需要我们不断地探索,不断地去发现。 我们对四边形的研究,还没有结束,大家课后可以用我们学到的基本思路继续探索研究直角梯形的定义、性质、判定。 设计意图:在完成本堂学习内容和学生一起作好小结的同时,我们引导学生继续研究直角梯形,使四边形的研究更加完整。
