初中数学人教版八年级下册 第十七章 勾股定理 数学活动教学设计(表格式)
文档属性
| 名称 | 初中数学人教版八年级下册 第十七章 勾股定理 数学活动教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 318.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 初中数学 年级 八年级 学期 春季
课题 勾股定理 数学活动
教学目标
1.理解并掌握勾股定理,运用勾股定理解决实际问题 2.通过拼图活动,体验数学思维的严谨,发展形象思维
教学内容
教学重点: 1.掌握勾股定理,理解勾股定理的证明;
2.能运用勾股定理解决具体问题.
教学难点: 1.利用拼图,数形结合的方法验证勾股定理;
2.探究数与形的内在联系.
教学过程
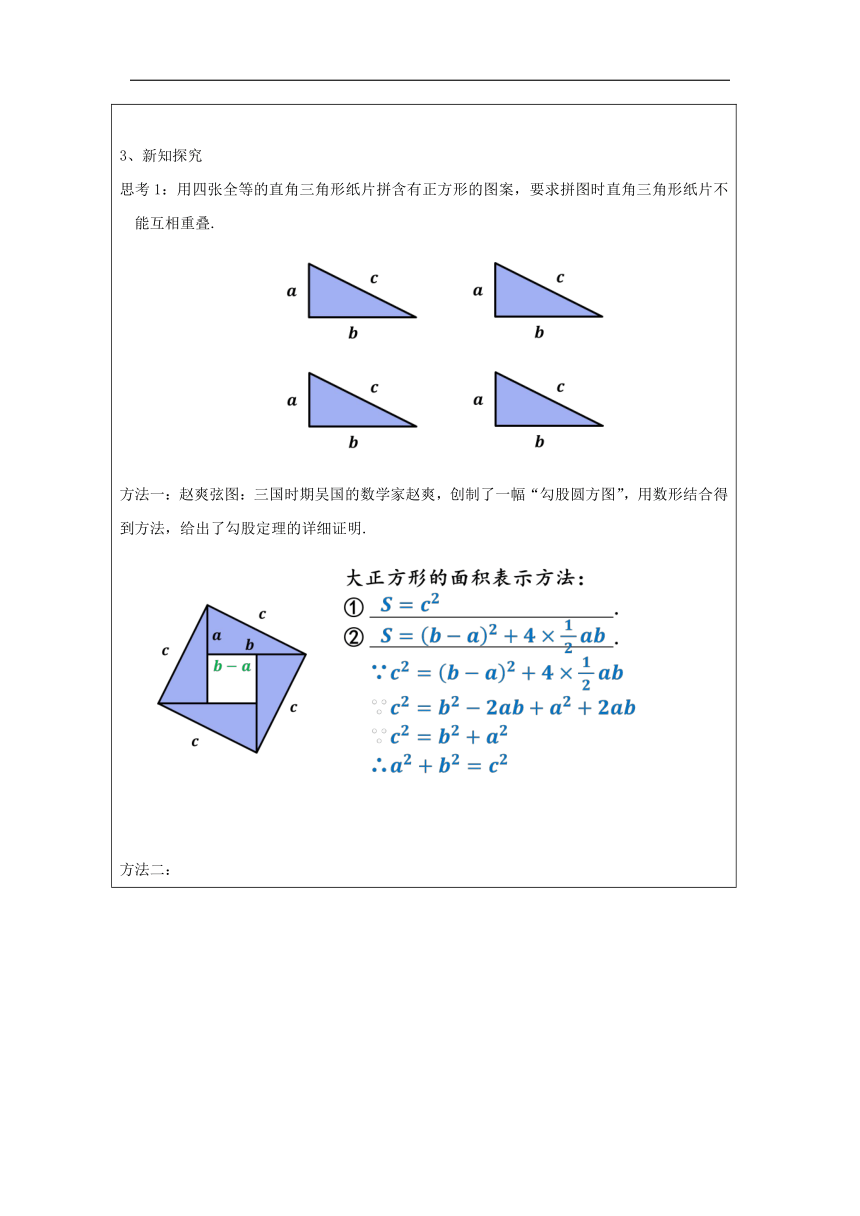
1、教学目标 1.理解并掌握勾股定理,运用勾股定理解决实际问题; 2.通过拼图活动,体验数学思维的严谨,发展形象思维. 2、情景导入:每周一的升旗仪式 学校需要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的总长度未知. 思考:应用勾股定理提出一个测量旗杆的高度的方案. 【设计意图】通过一个实际例子引入新课,激发学生的探究兴趣.可以让学生自主完成这个问题,体会数学与实际生活的紧密联系. 3、新知探究 思考1:用四张全等的直角三角形纸片拼含有正方形的图案,要求拼图时直角三角形纸片不能互相重叠. 方法一:赵爽弦图:三国时期吴国的数学家赵爽,创制了一幅“勾股圆方图”,用数形结合得到方法,给出了勾股定理的详细证明. 方法二: 思考2: 只用这两个直角三角形能说明吗? 解法: 【设计意图】通过拼图,利用面积法验证勾股定理,学生在观察与实践的过程中,锻炼克服困难的勇气,发展形象思维,培养探究能力和合作精神. 4、拓展提升 练习:(1)如图①,为直角三角形,正方形的面积为,正方形的面积为,则正方形的面积为________; (2)如图②,分别以直角三角形的三边长为直径向三角形外作三个半圆,则这三个半圆形的面积之间的关系式是________; (用图中字母表示) (3)如图③,如果直角三角形两直角边的长分别为和,分别以直角三角形的三边长为直径作半圆,请你利用(2)中得出的结论求阴影部分的面积. 【设计意图】给予直角三角形的基本图形,通过结合半圆型的变式,培养学生灵活应用勾股定理,解决面积的难题,培养数形结合的意识,突破难点,发展数学理念,提升思维能力. 5、小结
课程基本信息
学科 初中数学 年级 八年级 学期 春季
课题 勾股定理 数学活动
教学目标
1.理解并掌握勾股定理,运用勾股定理解决实际问题 2.通过拼图活动,体验数学思维的严谨,发展形象思维
教学内容
教学重点: 1.掌握勾股定理,理解勾股定理的证明;
2.能运用勾股定理解决具体问题.
教学难点: 1.利用拼图,数形结合的方法验证勾股定理;
2.探究数与形的内在联系.
教学过程
1、教学目标 1.理解并掌握勾股定理,运用勾股定理解决实际问题; 2.通过拼图活动,体验数学思维的严谨,发展形象思维. 2、情景导入:每周一的升旗仪式 学校需要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的总长度未知. 思考:应用勾股定理提出一个测量旗杆的高度的方案. 【设计意图】通过一个实际例子引入新课,激发学生的探究兴趣.可以让学生自主完成这个问题,体会数学与实际生活的紧密联系. 3、新知探究 思考1:用四张全等的直角三角形纸片拼含有正方形的图案,要求拼图时直角三角形纸片不能互相重叠. 方法一:赵爽弦图:三国时期吴国的数学家赵爽,创制了一幅“勾股圆方图”,用数形结合得到方法,给出了勾股定理的详细证明. 方法二: 思考2: 只用这两个直角三角形能说明吗? 解法: 【设计意图】通过拼图,利用面积法验证勾股定理,学生在观察与实践的过程中,锻炼克服困难的勇气,发展形象思维,培养探究能力和合作精神. 4、拓展提升 练习:(1)如图①,为直角三角形,正方形的面积为,正方形的面积为,则正方形的面积为________; (2)如图②,分别以直角三角形的三边长为直径向三角形外作三个半圆,则这三个半圆形的面积之间的关系式是________; (用图中字母表示) (3)如图③,如果直角三角形两直角边的长分别为和,分别以直角三角形的三边长为直径作半圆,请你利用(2)中得出的结论求阴影部分的面积. 【设计意图】给予直角三角形的基本图形,通过结合半圆型的变式,培养学生灵活应用勾股定理,解决面积的难题,培养数形结合的意识,突破难点,发展数学理念,提升思维能力. 5、小结
