初中数学人教八年级下册第十七章 勾股定理 数学活动:探折纸,找原理 教学设计(表格式)
文档属性
| 名称 | 初中数学人教八年级下册第十七章 勾股定理 数学活动:探折纸,找原理 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览




文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 数学活动:探折纸,找原理
教学目标
1. 经历折出60°,30°,15°的角,会用折角的原理及方法。 2.了解黄金矩形、黄金螺线的定义及它在生活中的应用,会用折边的原理及方法。 3.通过折纸活动,加深对轴对称、全等三角形、特殊的三角形、四边形等知识的认识,积累数学活动经验,发展学生的空间观念,建立几何直观,发展数学推理和运算能力。
教学内容
教学重点: 1. 会折自己想要的角、边,认识黄金矩形、黄金螺线。
2. 掌握折纸的数学原理、方法。
教学难点: 1. 制作黄金矩形、画出黄金螺线。
2. 掌握折纸的数学原理、方法。
教学过程
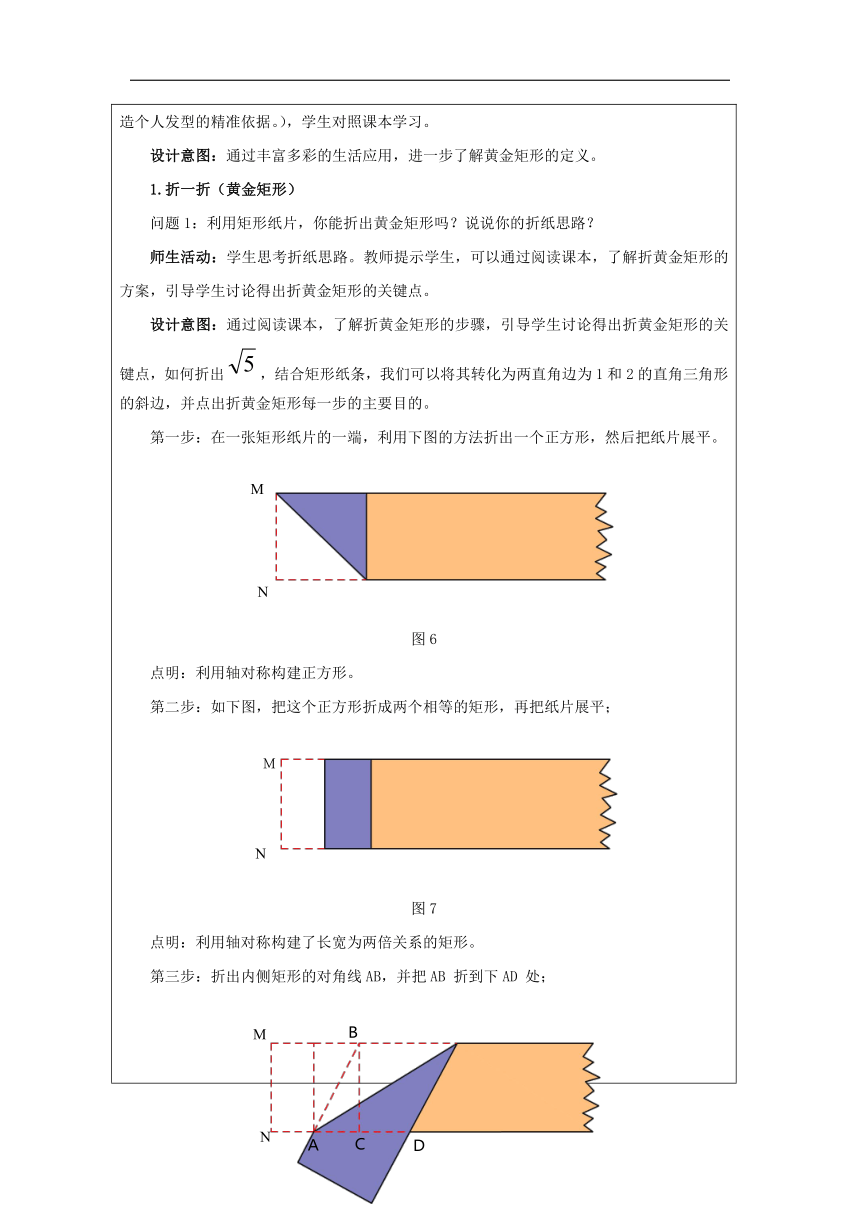
引言: 图1 折纸剪纸是我国一项传统的民间艺术,承载着我们童年的记忆。每逢春节、婚庆时,贴窗花、帖喜字是我们常见的一种民俗活动,被称为中华第一灯的仙居县针刺无骨花灯、不断创新的临海市张秀娟剪纸,成为浙江非遗文化传承中璀璨的明珠。它是中华民族伟大复兴中文化自信的生动体现。 同学们,今天让我们用数学的眼光来看一看折纸,在折纸探研的过程中,利用我们学过的特殊四边形、特殊三角形的边、角、对角线的性质和判定,寻找折纸背后的数学原理。 师生活动:教师讲解,学生倾听。 设计意图:从文化传承的角度出发,认识折纸剪纸;从学生生活出发,感受折纸文化;从民族复兴、文化自信出发,感受中国传统文化的博大精深;从折纸与数学的联系出发,旨在引导学生会用数学的眼光看世界。 一、探折角、找原理 1.折一折 问题1:利用矩形纸片,你能折出45°角吗?并说明理由。 图2 师生活动:学生试着去折,小组交流、总结。教师总结强调对折操作:点A落在矩形的另一边上,直角被平分成相等的两个角。 设计意图:从学生熟悉的生活体验出发,感知数学知识。 追问: 回顾你折出45°角的思考过程。 师生活动:各小组代表讲解思考过程,教师作好引导。根据矩形的性质,它的四个角都是直角,而45°是直角的一半,所以我们将折45°角转化为折出90°角的角平分线来处理。教师总结强调我们发现转化是一种重要的数学方法 设计意图:通过学生熟悉的直角对折得出45°,让学生回忆思考过程,引出对折问题一般转化为折角平分线的问题。 问题2 :利用矩形纸片,你能折出60°,30°,15°的角吗? 师生活动:通过学生自主探究,动手去折。教师观察、引导、参与讨论。 设计意图:通过学生自主探究,小组之间的讨论,找到想要折出的角的基本思路,然后动手折角,并验证正确性。 追问1:说说你是如何折出60°角的? 图3 师生活动:让学生讲解60°角的折纸过程,体会对折,会产生相等的边。利用等边三角形的判定、性质(三线合一),垂直平分线的性质,获得我们想要的角。 若学生从“在直角三角形中,30°角所对直角边是斜边的一半”这个性质考虑边之间的关系,先推出30°也可。 设计意图:通过60°典型角的折叠,让学生体会、得出折出想要角的思考、折叠过程,并能类比到其他角的折出。 追问2:说说你是如何折出30°,15°角? 师生活动:学生讲解,讨论。 设计意图:通过60°,30°,15°的折叠,让学生体会、得出对折是两等分一个角。 2.找原理 问题3:利用矩形是轴对称图形,折45°、60°、30°、15°角,我们发现了什么原理? 师生活动:通过学生小组之间的探讨、归纳,总结,得出:对折可以平分一个角,还可以把一个角分成2n 等份,同时通过角的和差得到相关的度数. 设计意图:要学生通过合作学习,得出折角主要的方法和规律。 问题4:回顾折角的过程中,你们用了哪些数学知识? 师生活动:通过小组合作讨论得出折角用到的数学知识,如:正方形和矩形的性质及判定、直角三角形的性质、勾股定理、角平分线、、等边三角形的性质…… 设计意图:通过小组合作,让学生实践联系理论,深挖折角背后的数学原理。 追问1:你觉得折角问题解决的思路是什么? 师生活动:通过小组合作总结得出:折角问题往往转化为特殊四边形、特殊三角形的知识来解决。 设计意图:通过小组合作,总结出:折角问题,我们该如何去设计折角的步骤,并折出我们想要的角。 3.小练习-你能折出你想要的角吗? 师生活动:学生实践操作,教师观察、指导。 设计意图:学生通过以自主探究、合作学习为主的课堂小练习,运用数学知识,设计折角的方案,并能验证其正确性。 二、探折角、找原理 (一)黄金螺线 图4:巴特农神庙 古希腊巴特农神庙,呈现出了非常舒服、非常和谐的矩形美,通过测量,我们发现它的宽和长的比是 (约为0.618).这就是黄金矩形。黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。 图5:黄金矩形的应用 师生活动:教师介绍(被评选为"世界新七大奇迹"的印度泰姬陵,它的设计处处体现了黄金矩形的设计风格。再比如说张秀娟老师的虎年作品,也体现了黄金矩形的设计理念。而达芬奇的不朽名著《蒙娜丽莎》,其构图更是黄金矩形的完美展示。黄金矩形,也是发型师打造个人发型的精准依据。),学生对照课本学习。 设计意图:通过丰富多彩的生活应用,进一步了解黄金矩形的定义。 1.折一折(黄金矩形) 问题1:利用矩形纸片,你能折出黄金矩形吗?说说你的折纸思路? 师生活动:学生思考折纸思路。教师提示学生,可以通过阅读课本,了解折黄金矩形的方案,引导学生讨论得出折黄金矩形的关键点。 设计意图:通过阅读课本,了解折黄金矩形的步骤,引导学生讨论得出折黄金矩形的关键点,如何折出,结合矩形纸条,我们可以将其转化为两直角边为1和2的直角三角形的斜边,并点出折黄金矩形每一步的主要目的。 第一步:在一张矩形纸片的一端,利用下图的方法折出一个正方形,然后把纸片展平。 图6 点明:利用轴对称构建正方形。 第二步:如下图,把这个正方形折成两个相等的矩形,再把纸片展平; 图7 点明:利用轴对称构建了长宽为两倍关系的矩形。 第三步:折出内侧矩形的对角线AB,并把AB 折到下AD 处; 图8 点明:利用轴对称构建了关键直角三角形的斜边和黄金矩形的关键边。 第四步:展平纸片,按照所得的点D 折出DE,得到矩形BCDE就是黄金矩形。 图9 点明:利用矩形的判定画出了黄金矩形。 2.探原理 问题2: 这样折出的矩形BCDE是黄金矩形吗?也就是说,宽CD与长BC 的比值是否为 ? 图10 解题思路:假设矩形纸条的宽为2,则BC=2, 那么AC=1,根据勾股定理可得AB=。由对折可得AD=AB=,CD=AD-AC=-1,得到 。 师生活动:学生小组合作,证明矩形BCDE是黄金矩形。教师聆听、参加讨论。 设计意图:引导学生通过观察、猜想、证明,这样一个方法证明矩形BCDE是黄金矩形。 问题3: 矩形MNDE是黄金矩形吗?请说明理由. 图11 解题思路:由上题可知:NM=2,AB=AD=,AN=1,所以ND=+1 ∴宽比长=利用平方差公式,分母有理化得,∴矩形MNDE是黄金矩形 师生活动:学生小组合作,证明矩形MNDE是黄金矩形。教师聆听、参加讨论。 设计意图:引导学生通过观察、猜想、证明,这样一个方法证明矩形MNDE是黄金矩形,培养学生的发散思维,并为研究黄金螺线埋下伏笔。 (二)黄金螺线 1.折一折 问题4:矩形BCDE、矩形MNDE都是黄金矩形,那么四边形NCBM是什么图形? 师生活动:通过师生问答的形式,得出黄金矩形MNDE的宽为边长的正方形。 追问:在黄金矩形BCDE中,你能快速地折出多少个新的黄金矩形? 图12 师生活动:通过数学推理,师生问答引导学生得出理论上讲可以折出无数个新的黄金矩形。 设计意图:通过黄金矩形中快速折黄金矩形,为下面引出黄金螺线作铺垫。 2.画一画 问题5:将这些正方形内的四分之一圆弧连接起来,你会发现什么新的图形? 图13 师生活动:学生动手操作及画图,得出新的图形是一条平滑的螺线,即黄金螺线。教师观察引导。 设计意图:通过观察、猜想、证明,并通过学生动手操作,画出黄金螺线,引出其定义,培养学生几何直观、数学推理。 图13 黄金螺线在现实生活中非常常见,如建筑物的楼梯,拍照时的构图,大到宇宙中的银河,超级台风的台风眼,小到海螺,花、草的生长情况,所以黄金螺线又被称为生长螺线。 3.小练习——画一条黄金螺线 师生活动:学生实践操作,教师观察、指导。 设计意图:学生通过以自主探究、合作学习为主的课堂小练习,运用数学知识,动手操作,选取最佳方案,并能验证其正确性。 4.找原理 折边用到的数学知识有: 矩形的性质及判定,直角三角形的性质、勾股定理、角平分线的定义、平行线的性质、等边三角形的性质、全等三角形的性质及判定…… 折边学到的思想方法有: 勾股定理是折边问题的关键 折边问题可以转化为特殊四边形,特殊三角形的知识和方法来解决。 数形结合的思想,转化的思想 师生活动:师生共同讨论,归纳总结,要折出自己想要的边的方法、规律。 设计意图:通过阶段性小结,得出折边的方法规律。 课堂小结 纸活动的基本思路: 1.折纸活动的研究内容是什么? 2.折纸活动的研究步骤是什么? 3.折纸活动的研究方法是什么? 师生活动:通过师生之间讨论、交流,教师要引导学生进行课堂小结。 (本堂课通过研究折角、折边,对特殊四边形、特殊三角形的相关知识,作了一个深入的回顾、复习、应用,现在我想请大家说说,你们有什么新的收获。 折纸活动的基本思路: 我们从研究的内容看:我们研究了四边形与三角形之间的角、边的关系(重点讲了对折将角平分成2n等份,黄金矩形、黄金螺线) 我们从研究的步骤看:先折纸,再证明,后应用 我们从研究的方法看:转化的思想、数形结合的思想) 设计意图:通过小结的形式,引导学生得出数学活动——折纸的研究内容、步骤、方法,这是几何研究的基本思路,也是本章平行四边形研究的基本思路。 四、布置作业 同学们,传统文化源远流长传承不息,我们对折纸的探索也永不停息。这是我们今天的作业: 作业: 1.探究黄金三角形; 2.你还能折出新的作品并说明这样折的道理吗? 师生活动:教师布置作业,学生聆听。 设计意图:给学生更大的研究空间,希望学生传承折纸、剪纸文化,继续深挖折纸背后数学原理。
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 数学活动:探折纸,找原理
教学目标
1. 经历折出60°,30°,15°的角,会用折角的原理及方法。 2.了解黄金矩形、黄金螺线的定义及它在生活中的应用,会用折边的原理及方法。 3.通过折纸活动,加深对轴对称、全等三角形、特殊的三角形、四边形等知识的认识,积累数学活动经验,发展学生的空间观念,建立几何直观,发展数学推理和运算能力。
教学内容
教学重点: 1. 会折自己想要的角、边,认识黄金矩形、黄金螺线。
2. 掌握折纸的数学原理、方法。
教学难点: 1. 制作黄金矩形、画出黄金螺线。
2. 掌握折纸的数学原理、方法。
教学过程
引言: 图1 折纸剪纸是我国一项传统的民间艺术,承载着我们童年的记忆。每逢春节、婚庆时,贴窗花、帖喜字是我们常见的一种民俗活动,被称为中华第一灯的仙居县针刺无骨花灯、不断创新的临海市张秀娟剪纸,成为浙江非遗文化传承中璀璨的明珠。它是中华民族伟大复兴中文化自信的生动体现。 同学们,今天让我们用数学的眼光来看一看折纸,在折纸探研的过程中,利用我们学过的特殊四边形、特殊三角形的边、角、对角线的性质和判定,寻找折纸背后的数学原理。 师生活动:教师讲解,学生倾听。 设计意图:从文化传承的角度出发,认识折纸剪纸;从学生生活出发,感受折纸文化;从民族复兴、文化自信出发,感受中国传统文化的博大精深;从折纸与数学的联系出发,旨在引导学生会用数学的眼光看世界。 一、探折角、找原理 1.折一折 问题1:利用矩形纸片,你能折出45°角吗?并说明理由。 图2 师生活动:学生试着去折,小组交流、总结。教师总结强调对折操作:点A落在矩形的另一边上,直角被平分成相等的两个角。 设计意图:从学生熟悉的生活体验出发,感知数学知识。 追问: 回顾你折出45°角的思考过程。 师生活动:各小组代表讲解思考过程,教师作好引导。根据矩形的性质,它的四个角都是直角,而45°是直角的一半,所以我们将折45°角转化为折出90°角的角平分线来处理。教师总结强调我们发现转化是一种重要的数学方法 设计意图:通过学生熟悉的直角对折得出45°,让学生回忆思考过程,引出对折问题一般转化为折角平分线的问题。 问题2 :利用矩形纸片,你能折出60°,30°,15°的角吗? 师生活动:通过学生自主探究,动手去折。教师观察、引导、参与讨论。 设计意图:通过学生自主探究,小组之间的讨论,找到想要折出的角的基本思路,然后动手折角,并验证正确性。 追问1:说说你是如何折出60°角的? 图3 师生活动:让学生讲解60°角的折纸过程,体会对折,会产生相等的边。利用等边三角形的判定、性质(三线合一),垂直平分线的性质,获得我们想要的角。 若学生从“在直角三角形中,30°角所对直角边是斜边的一半”这个性质考虑边之间的关系,先推出30°也可。 设计意图:通过60°典型角的折叠,让学生体会、得出折出想要角的思考、折叠过程,并能类比到其他角的折出。 追问2:说说你是如何折出30°,15°角? 师生活动:学生讲解,讨论。 设计意图:通过60°,30°,15°的折叠,让学生体会、得出对折是两等分一个角。 2.找原理 问题3:利用矩形是轴对称图形,折45°、60°、30°、15°角,我们发现了什么原理? 师生活动:通过学生小组之间的探讨、归纳,总结,得出:对折可以平分一个角,还可以把一个角分成2n 等份,同时通过角的和差得到相关的度数. 设计意图:要学生通过合作学习,得出折角主要的方法和规律。 问题4:回顾折角的过程中,你们用了哪些数学知识? 师生活动:通过小组合作讨论得出折角用到的数学知识,如:正方形和矩形的性质及判定、直角三角形的性质、勾股定理、角平分线、、等边三角形的性质…… 设计意图:通过小组合作,让学生实践联系理论,深挖折角背后的数学原理。 追问1:你觉得折角问题解决的思路是什么? 师生活动:通过小组合作总结得出:折角问题往往转化为特殊四边形、特殊三角形的知识来解决。 设计意图:通过小组合作,总结出:折角问题,我们该如何去设计折角的步骤,并折出我们想要的角。 3.小练习-你能折出你想要的角吗? 师生活动:学生实践操作,教师观察、指导。 设计意图:学生通过以自主探究、合作学习为主的课堂小练习,运用数学知识,设计折角的方案,并能验证其正确性。 二、探折角、找原理 (一)黄金螺线 图4:巴特农神庙 古希腊巴特农神庙,呈现出了非常舒服、非常和谐的矩形美,通过测量,我们发现它的宽和长的比是 (约为0.618).这就是黄金矩形。黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。 图5:黄金矩形的应用 师生活动:教师介绍(被评选为"世界新七大奇迹"的印度泰姬陵,它的设计处处体现了黄金矩形的设计风格。再比如说张秀娟老师的虎年作品,也体现了黄金矩形的设计理念。而达芬奇的不朽名著《蒙娜丽莎》,其构图更是黄金矩形的完美展示。黄金矩形,也是发型师打造个人发型的精准依据。),学生对照课本学习。 设计意图:通过丰富多彩的生活应用,进一步了解黄金矩形的定义。 1.折一折(黄金矩形) 问题1:利用矩形纸片,你能折出黄金矩形吗?说说你的折纸思路? 师生活动:学生思考折纸思路。教师提示学生,可以通过阅读课本,了解折黄金矩形的方案,引导学生讨论得出折黄金矩形的关键点。 设计意图:通过阅读课本,了解折黄金矩形的步骤,引导学生讨论得出折黄金矩形的关键点,如何折出,结合矩形纸条,我们可以将其转化为两直角边为1和2的直角三角形的斜边,并点出折黄金矩形每一步的主要目的。 第一步:在一张矩形纸片的一端,利用下图的方法折出一个正方形,然后把纸片展平。 图6 点明:利用轴对称构建正方形。 第二步:如下图,把这个正方形折成两个相等的矩形,再把纸片展平; 图7 点明:利用轴对称构建了长宽为两倍关系的矩形。 第三步:折出内侧矩形的对角线AB,并把AB 折到下AD 处; 图8 点明:利用轴对称构建了关键直角三角形的斜边和黄金矩形的关键边。 第四步:展平纸片,按照所得的点D 折出DE,得到矩形BCDE就是黄金矩形。 图9 点明:利用矩形的判定画出了黄金矩形。 2.探原理 问题2: 这样折出的矩形BCDE是黄金矩形吗?也就是说,宽CD与长BC 的比值是否为 ? 图10 解题思路:假设矩形纸条的宽为2,则BC=2, 那么AC=1,根据勾股定理可得AB=。由对折可得AD=AB=,CD=AD-AC=-1,得到 。 师生活动:学生小组合作,证明矩形BCDE是黄金矩形。教师聆听、参加讨论。 设计意图:引导学生通过观察、猜想、证明,这样一个方法证明矩形BCDE是黄金矩形。 问题3: 矩形MNDE是黄金矩形吗?请说明理由. 图11 解题思路:由上题可知:NM=2,AB=AD=,AN=1,所以ND=+1 ∴宽比长=利用平方差公式,分母有理化得,∴矩形MNDE是黄金矩形 师生活动:学生小组合作,证明矩形MNDE是黄金矩形。教师聆听、参加讨论。 设计意图:引导学生通过观察、猜想、证明,这样一个方法证明矩形MNDE是黄金矩形,培养学生的发散思维,并为研究黄金螺线埋下伏笔。 (二)黄金螺线 1.折一折 问题4:矩形BCDE、矩形MNDE都是黄金矩形,那么四边形NCBM是什么图形? 师生活动:通过师生问答的形式,得出黄金矩形MNDE的宽为边长的正方形。 追问:在黄金矩形BCDE中,你能快速地折出多少个新的黄金矩形? 图12 师生活动:通过数学推理,师生问答引导学生得出理论上讲可以折出无数个新的黄金矩形。 设计意图:通过黄金矩形中快速折黄金矩形,为下面引出黄金螺线作铺垫。 2.画一画 问题5:将这些正方形内的四分之一圆弧连接起来,你会发现什么新的图形? 图13 师生活动:学生动手操作及画图,得出新的图形是一条平滑的螺线,即黄金螺线。教师观察引导。 设计意图:通过观察、猜想、证明,并通过学生动手操作,画出黄金螺线,引出其定义,培养学生几何直观、数学推理。 图13 黄金螺线在现实生活中非常常见,如建筑物的楼梯,拍照时的构图,大到宇宙中的银河,超级台风的台风眼,小到海螺,花、草的生长情况,所以黄金螺线又被称为生长螺线。 3.小练习——画一条黄金螺线 师生活动:学生实践操作,教师观察、指导。 设计意图:学生通过以自主探究、合作学习为主的课堂小练习,运用数学知识,动手操作,选取最佳方案,并能验证其正确性。 4.找原理 折边用到的数学知识有: 矩形的性质及判定,直角三角形的性质、勾股定理、角平分线的定义、平行线的性质、等边三角形的性质、全等三角形的性质及判定…… 折边学到的思想方法有: 勾股定理是折边问题的关键 折边问题可以转化为特殊四边形,特殊三角形的知识和方法来解决。 数形结合的思想,转化的思想 师生活动:师生共同讨论,归纳总结,要折出自己想要的边的方法、规律。 设计意图:通过阶段性小结,得出折边的方法规律。 课堂小结 纸活动的基本思路: 1.折纸活动的研究内容是什么? 2.折纸活动的研究步骤是什么? 3.折纸活动的研究方法是什么? 师生活动:通过师生之间讨论、交流,教师要引导学生进行课堂小结。 (本堂课通过研究折角、折边,对特殊四边形、特殊三角形的相关知识,作了一个深入的回顾、复习、应用,现在我想请大家说说,你们有什么新的收获。 折纸活动的基本思路: 我们从研究的内容看:我们研究了四边形与三角形之间的角、边的关系(重点讲了对折将角平分成2n等份,黄金矩形、黄金螺线) 我们从研究的步骤看:先折纸,再证明,后应用 我们从研究的方法看:转化的思想、数形结合的思想) 设计意图:通过小结的形式,引导学生得出数学活动——折纸的研究内容、步骤、方法,这是几何研究的基本思路,也是本章平行四边形研究的基本思路。 四、布置作业 同学们,传统文化源远流长传承不息,我们对折纸的探索也永不停息。这是我们今天的作业: 作业: 1.探究黄金三角形; 2.你还能折出新的作品并说明这样折的道理吗? 师生活动:教师布置作业,学生聆听。 设计意图:给学生更大的研究空间,希望学生传承折纸、剪纸文化,继续深挖折纸背后数学原理。
