数学人教A版(2019)必修第二册8.6.1直线与直线垂直(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.6.1直线与直线垂直(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
复习导入
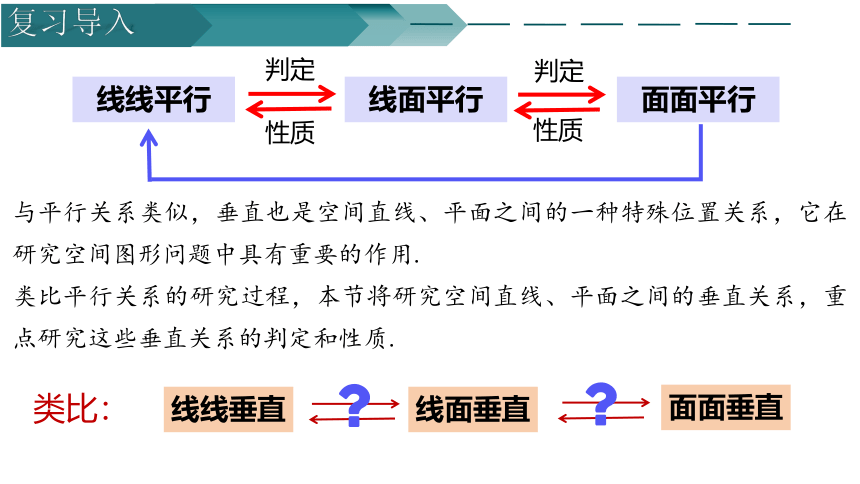
与平行关系类似,垂直也是空间直线、平面之间的一种特殊位置关系,它在研究空间图形问题中具有重要的作用.
类比平行关系的研究过程,本节将研究空间直线、平面之间的垂直关系,重点研究这些垂直关系的判定和性质.
面面平行
判定
性质
线线平行
线面平行
判定
性质
类比:
线线垂直
线面垂直
面面垂直
新知探究
共面直线
异面直线:
平行直线:
相交直线:
在同一平面内,有且只有一个公共点;
在同一平面内,没有公共点;
不同在任何一个平面内,没有公共点.
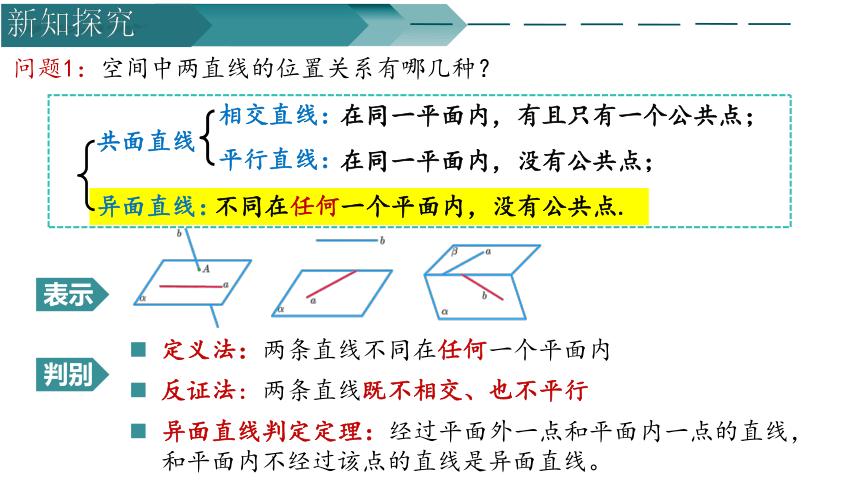
问题1:空间中两直线的位置关系有哪几种?
表示
判别
定义法:两条直线不同在任何一个平面内
反证法:两条直线既不相交、也不平行
异面直线判定定理:经过平面外一点和平面内一点的直线,和平面内不经过该点的直线是异面直线。
新知探究
共面直线
异面直线:
平行直线:
相交直线:
在同一平面内,有且只有一个公共点;
在同一平面内,没有公共点;
不同在任何一个平面内,没有公共点.
问题1:空间中两直线的位置关系有哪几种?
问题2:在平面内,两直线所成的角是什么?
平面内相交直线所成的角:
在平面内,两条直线相交成四个角,其中不大于的角称为它们的夹角,它刻画了一条直线相对于另一条直线倾斜的程度.
新知探究
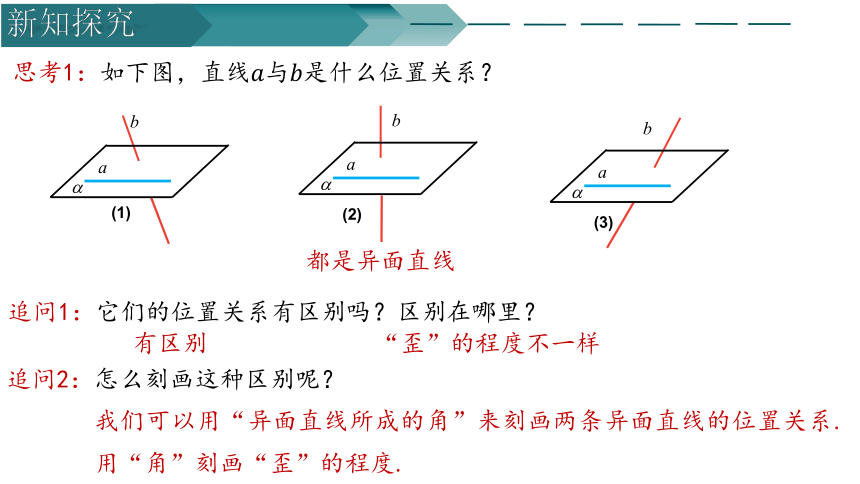
思考1:如下图,直线与是什么位置关系?
(1)
(2)
(3)
都是异面直线
追问1:它们的位置关系有区别吗?区别在哪里?
追问2:怎么刻画这种区别呢?
有区别
“歪”的程度不一样
我们可以用“异面直线所成的角”来刻画两条异面直线的位置关系.用“角”刻画“歪”的程度.
新知探究
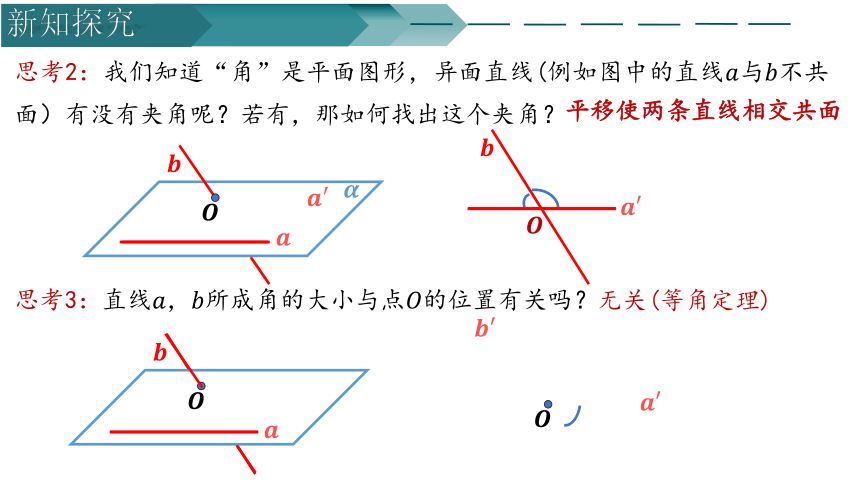
思考2:我们知道“角”是平面图形,异面直线(例如图中的直线与不共面)有没有夹角呢?若有,那如何找出这个夹角?
平移使两条直线相交共面
思考3:直线所成角的大小与点的位置有关吗?
无关(等角定理)
已知两条异面直线经过空间任一点分别作直线我们把直线与所成的角叫做异面直线与所成的角(或夹角).
异面直线所成角
新知探究
(异面直线平移至共面——空间问题平面化)
异面直线所成角的取值范围:
特例:
①当两条直线相互平行(共面直线)时,我们规定它们所成的角为. 所以空间中两条直线所成角的取值范围是
②如果两条异面直线所成的角是直角(),那么称这两条异面
直线互相垂直.直线与直线垂直,记作.
新知探究
思考4:如果空间两条直线垂直,那么它们一定相交吗?
不一定,可能是相交垂直,还可能是异面垂直.
空间中两直线垂直
异面垂直:
相交垂直:
有垂足
无垂足
练习巩固
例1:如图,已知正方体.
(1)哪些棱所在直线与直线垂直?
(2)求直线与所成角的大小.
(3)求直线与所成角的大小.
题型一:求异面直线所成角
直接平移法
可利用图中已有的平行线
变式1-1:如图,在正方体中, 是点,求异面直线与所成角的大小。
练习巩固 大册P101例2
中位线平移法
在原正方体右侧补一个全等的正方体
变式1-2:如图,在正方体中, 是点,求异面直线与所成角的大小。
补形平移法
在已知图形中,补做一个相同的几何体,以便找到平行线
求角的值,常利用解三角形等知识得出
练习巩固 大册P101例2
练习巩固 大册P100延伸探究
变式1-3:如图,如图,在四面体中,分别为的中点,求和所成的角.
解:∵E,F,G分别是所在棱的中点,
∴GE∥CD,GF∥AB.
∴∠EGF或其补角即为AB与CD所成的角.
由已知可得GE=GF=1,又EF= ,
∴由余弦定理,得∠EGF=120°.
∴异面直线AB与CD所成的角为60°.
注意:异面直线所成角的范围是 (锐角或直角)
例2:如图,在正方体中, 为底面的中心.
求证.
题型二:证明两异面直线垂直
从例1与例2的解答可以看出,为了简便,在求作异面直线所成的角时,点常选在其中的一条直线上 (如线段的端点,线段的中点等).
练习巩固
练习巩固
变式2-1:如图,在正方体中,求证: ⊥
证明:如图(2),连接交于,
取的中点为,连接.
∵为中点,∴.
∴直线与所成的角即为直线与所成的角.
连接,易证又为的中点,
∴.∴.
练习巩固 大册P102易错辨析
例3:如图,在四面体中,分别是的中点.若所成的角为,且.求的长度.
题型三:异面直线所成角的应用
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
复习导入
与平行关系类似,垂直也是空间直线、平面之间的一种特殊位置关系,它在研究空间图形问题中具有重要的作用.
类比平行关系的研究过程,本节将研究空间直线、平面之间的垂直关系,重点研究这些垂直关系的判定和性质.
面面平行
判定
性质
线线平行
线面平行
判定
性质
类比:
线线垂直
线面垂直
面面垂直
新知探究
共面直线
异面直线:
平行直线:
相交直线:
在同一平面内,有且只有一个公共点;
在同一平面内,没有公共点;
不同在任何一个平面内,没有公共点.
问题1:空间中两直线的位置关系有哪几种?
表示
判别
定义法:两条直线不同在任何一个平面内
反证法:两条直线既不相交、也不平行
异面直线判定定理:经过平面外一点和平面内一点的直线,和平面内不经过该点的直线是异面直线。
新知探究
共面直线
异面直线:
平行直线:
相交直线:
在同一平面内,有且只有一个公共点;
在同一平面内,没有公共点;
不同在任何一个平面内,没有公共点.
问题1:空间中两直线的位置关系有哪几种?
问题2:在平面内,两直线所成的角是什么?
平面内相交直线所成的角:
在平面内,两条直线相交成四个角,其中不大于的角称为它们的夹角,它刻画了一条直线相对于另一条直线倾斜的程度.
新知探究
思考1:如下图,直线与是什么位置关系?
(1)
(2)
(3)
都是异面直线
追问1:它们的位置关系有区别吗?区别在哪里?
追问2:怎么刻画这种区别呢?
有区别
“歪”的程度不一样
我们可以用“异面直线所成的角”来刻画两条异面直线的位置关系.用“角”刻画“歪”的程度.
新知探究
思考2:我们知道“角”是平面图形,异面直线(例如图中的直线与不共面)有没有夹角呢?若有,那如何找出这个夹角?
平移使两条直线相交共面
思考3:直线所成角的大小与点的位置有关吗?
无关(等角定理)
已知两条异面直线经过空间任一点分别作直线我们把直线与所成的角叫做异面直线与所成的角(或夹角).
异面直线所成角
新知探究
(异面直线平移至共面——空间问题平面化)
异面直线所成角的取值范围:
特例:
①当两条直线相互平行(共面直线)时,我们规定它们所成的角为. 所以空间中两条直线所成角的取值范围是
②如果两条异面直线所成的角是直角(),那么称这两条异面
直线互相垂直.直线与直线垂直,记作.
新知探究
思考4:如果空间两条直线垂直,那么它们一定相交吗?
不一定,可能是相交垂直,还可能是异面垂直.
空间中两直线垂直
异面垂直:
相交垂直:
有垂足
无垂足
练习巩固
例1:如图,已知正方体.
(1)哪些棱所在直线与直线垂直?
(2)求直线与所成角的大小.
(3)求直线与所成角的大小.
题型一:求异面直线所成角
直接平移法
可利用图中已有的平行线
变式1-1:如图,在正方体中, 是点,求异面直线与所成角的大小。
练习巩固 大册P101例2
中位线平移法
在原正方体右侧补一个全等的正方体
变式1-2:如图,在正方体中, 是点,求异面直线与所成角的大小。
补形平移法
在已知图形中,补做一个相同的几何体,以便找到平行线
求角的值,常利用解三角形等知识得出
练习巩固 大册P101例2
练习巩固 大册P100延伸探究
变式1-3:如图,如图,在四面体中,分别为的中点,求和所成的角.
解:∵E,F,G分别是所在棱的中点,
∴GE∥CD,GF∥AB.
∴∠EGF或其补角即为AB与CD所成的角.
由已知可得GE=GF=1,又EF= ,
∴由余弦定理,得∠EGF=120°.
∴异面直线AB与CD所成的角为60°.
注意:异面直线所成角的范围是 (锐角或直角)
例2:如图,在正方体中, 为底面的中心.
求证.
题型二:证明两异面直线垂直
从例1与例2的解答可以看出,为了简便,在求作异面直线所成的角时,点常选在其中的一条直线上 (如线段的端点,线段的中点等).
练习巩固
练习巩固
变式2-1:如图,在正方体中,求证: ⊥
证明:如图(2),连接交于,
取的中点为,连接.
∵为中点,∴.
∴直线与所成的角即为直线与所成的角.
连接,易证又为的中点,
∴.∴.
练习巩固 大册P102易错辨析
例3:如图,在四面体中,分别是的中点.若所成的角为,且.求的长度.
题型三:异面直线所成角的应用
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
