数学人教A版(2019)必修第二册7.1.1数系的扩充和复数的概念(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册7.1.1数系的扩充和复数的概念(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 16:50:18 | ||
图片预览






文档简介
(共19张PPT)
必修第二册第七章《复数》
7.1.1 数系的扩充和复数的概念
学习复数是对数系认识的一次飞跃
探究点1 数系的扩充
数的概念——发展的动力:
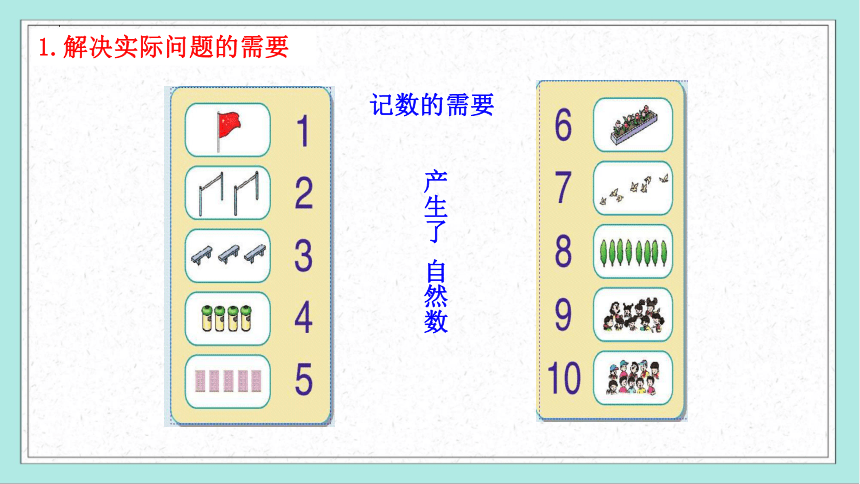
1.解决实际问题的需要.
2.解方程的需要.
思考:下列集合间的关系?
记数的需要
产生了 自然数
1.解决实际问题的需要
为了表示各种具有相反意义的量以及满足记数的需要——
负数
产生了 分数
分配、测量中的等分
其实,这就是后来人们发现的“无理数”
一个学生画了一个边长为1的正方形.
根据勾股定理
可见对角线的长度是存在的,可它是多少
设对角线长为x.
为了解决度量正方形对角线长的问题产生了
——无理数(无限不循环小数).
2.数学内部发展的需要
自然数集N
整数集Z
引入负数(负号)
引入分数(分数线)
有理数集Q
引入无理数(根号)
实数集R
引入?数
?数集
正方形对角线的度量
复数是16世纪人们在讨论一元二次方程、一元三次方程的求根公式时引入的。
复数在数学、力学、电学及其他学科中都有广泛的应用。
复数与向量、平面解析几何、三角函数等都有密切的联系。
扩充后的数系中规定的加/乘法运算与原数系的加/乘法运算协调一致.
如:Q中的加/乘法交换律、结合律等
R中也适用
探究点2复数的概念实数解决方程x2+1=0在实数集中无解的问题:a+bi为了解决负数开平方问题,数学家大胆引入一个新数i,把i叫做虚数单位,并且规定:(2)实数可以与i进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立.(1) 1;注:虚数单位i是瑞士数学家欧拉最早引用的,它取自imaginary(想象的,假想的)一词的词头. 由它所创造的复变函数理论,成为解决电磁理论,航空理论,原子能及核物理等尖端科学的数学工具.
实际应用
依此规则,我们
①把实数b与i相乘,结果记作bi
②把实数a与bi相加,结果记作a+bi
所有实数以及i都可写成a+bi (a,b∈R)的形式,从而这些数都在扩充后的新数集中,我们把形如a+bi (a,b∈R)的数叫做复数.
1. 复数的概念
形如a+bi (a,b∈R)的数叫做复数.
i 叫做虚数单位.
全体复数所构成的集合C={a+bi |a,b∈R}叫做复数集.
复数通常用字母z表示,即
z=a+bi (a,b∈R)
2. 复数的代数形式
a叫做复数的实部
b叫做复数的虚部
注意:复数z的实部和虚部都是 数.
-3
实
1.复数i-2的虚部是( )
A.i B. -2 C.1 D.2
C
这些都叫复数,
有些是实数,
有些还能叫虚数,有些还能叫纯虚数
z=a+bi (a,b∈R)
当且仅当 b=0 时,它叫做
当且仅当 b≠0 时,它叫做
当且仅当a=b=0时,它是实数0;
z=a
z=0
z=a+bi (b≠0)
z=bi (b≠0)
虚数
实数
当且仅当 时,它叫做
a=0
b≠0
纯虚数
3. 复数的分类
复数
实数:
虚数:
纯虚数:
非纯虚数:
思考4 复数集C与实数集R之间有什么关系?
复
数
集
C
虚数集
实数集
R
纯虚数集
虚数
纯虚数
实数
例1
解:当m-1=0时,即m=1时,复数z 是实数;
当m-1≠0时,即m≠1时,复数z 是虚数;
当m+1=0,且m-1≠0时,即m=-1时,复数z 是纯虚数.
4. 复数相等复数
如果两个复数的实部和虚部分别相等,那么我们就说这两个复
数相等.即如果 ,那么
例2 求适合下列方程的实数x与y的值:
(1) (2)
课堂小结
2.虚数单位i的引入;
1.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
课堂练习
必修第二册第七章《复数》
7.1.1 数系的扩充和复数的概念
学习复数是对数系认识的一次飞跃
探究点1 数系的扩充
数的概念——发展的动力:
1.解决实际问题的需要.
2.解方程的需要.
思考:下列集合间的关系?
记数的需要
产生了 自然数
1.解决实际问题的需要
为了表示各种具有相反意义的量以及满足记数的需要——
负数
产生了 分数
分配、测量中的等分
其实,这就是后来人们发现的“无理数”
一个学生画了一个边长为1的正方形.
根据勾股定理
可见对角线的长度是存在的,可它是多少
设对角线长为x.
为了解决度量正方形对角线长的问题产生了
——无理数(无限不循环小数).
2.数学内部发展的需要
自然数集N
整数集Z
引入负数(负号)
引入分数(分数线)
有理数集Q
引入无理数(根号)
实数集R
引入?数
?数集
正方形对角线的度量
复数是16世纪人们在讨论一元二次方程、一元三次方程的求根公式时引入的。
复数在数学、力学、电学及其他学科中都有广泛的应用。
复数与向量、平面解析几何、三角函数等都有密切的联系。
扩充后的数系中规定的加/乘法运算与原数系的加/乘法运算协调一致.
如:Q中的加/乘法交换律、结合律等
R中也适用
探究点2复数的概念实数解决方程x2+1=0在实数集中无解的问题:a+bi为了解决负数开平方问题,数学家大胆引入一个新数i,把i叫做虚数单位,并且规定:(2)实数可以与i进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立.(1) 1;注:虚数单位i是瑞士数学家欧拉最早引用的,它取自imaginary(想象的,假想的)一词的词头. 由它所创造的复变函数理论,成为解决电磁理论,航空理论,原子能及核物理等尖端科学的数学工具.
实际应用
依此规则,我们
①把实数b与i相乘,结果记作bi
②把实数a与bi相加,结果记作a+bi
所有实数以及i都可写成a+bi (a,b∈R)的形式,从而这些数都在扩充后的新数集中,我们把形如a+bi (a,b∈R)的数叫做复数.
1. 复数的概念
形如a+bi (a,b∈R)的数叫做复数.
i 叫做虚数单位.
全体复数所构成的集合C={a+bi |a,b∈R}叫做复数集.
复数通常用字母z表示,即
z=a+bi (a,b∈R)
2. 复数的代数形式
a叫做复数的实部
b叫做复数的虚部
注意:复数z的实部和虚部都是 数.
-3
实
1.复数i-2的虚部是( )
A.i B. -2 C.1 D.2
C
这些都叫复数,
有些是实数,
有些还能叫虚数,有些还能叫纯虚数
z=a+bi (a,b∈R)
当且仅当 b=0 时,它叫做
当且仅当 b≠0 时,它叫做
当且仅当a=b=0时,它是实数0;
z=a
z=0
z=a+bi (b≠0)
z=bi (b≠0)
虚数
实数
当且仅当 时,它叫做
a=0
b≠0
纯虚数
3. 复数的分类
复数
实数:
虚数:
纯虚数:
非纯虚数:
思考4 复数集C与实数集R之间有什么关系?
复
数
集
C
虚数集
实数集
R
纯虚数集
虚数
纯虚数
实数
例1
解:当m-1=0时,即m=1时,复数z 是实数;
当m-1≠0时,即m≠1时,复数z 是虚数;
当m+1=0,且m-1≠0时,即m=-1时,复数z 是纯虚数.
4. 复数相等复数
如果两个复数的实部和虚部分别相等,那么我们就说这两个复
数相等.即如果 ,那么
例2 求适合下列方程的实数x与y的值:
(1) (2)
课堂小结
2.虚数单位i的引入;
1.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
课堂练习
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
