第六单元 圆(复习课件)-五年级数学下学期期末核心考点集训(苏教版)(共25张PPT)
文档属性
| 名称 | 第六单元 圆(复习课件)-五年级数学下学期期末核心考点集训(苏教版)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第六单元 圆
五年级下册 苏教版
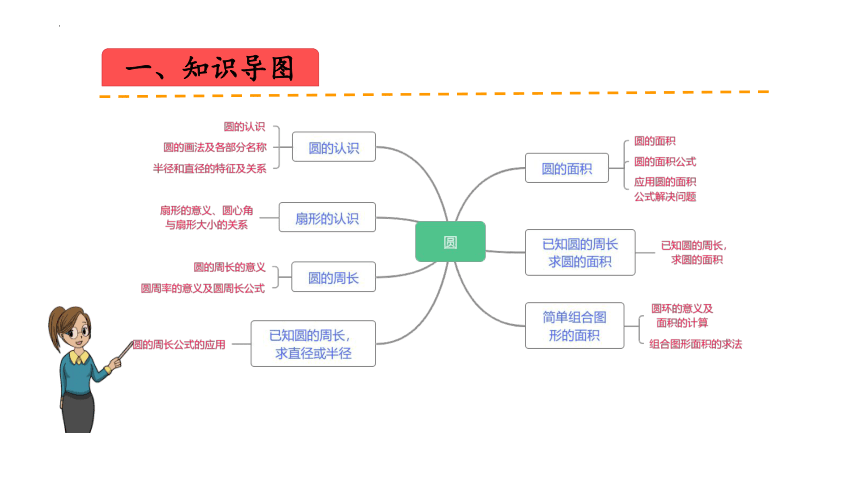
一、知识导图
二、考点梳理
知识点① 圆的认识
1.圆是由曲线围成的封闭图形。
2.用圆规画圆时,针尖固定的一点是圆心,连接圆心和圆上任意一点的线段是半径,通过圆心并且两端都在圆上的线段是直径。
3.圆有无数条直径和半径。在同圆或等圆中,直径的长度是半径的2倍,半径的长度是直径的一半,用字母表示为d=2r或r= 。
4.圆是轴对称图形,有无数条对称轴。
二、考点梳理
知识点② 扇形的认识
1.扇形:一条弧和经过这条弧两端点的两条半径所围成的图形叫作扇形。
2.扇形的大小:在同圆或等圆中,扇形的大小与圆心角的大小有关,圆心角大的扇形大,圆心角小的扇形小。
二、考点梳理
知识点③ 圆的周长
1.圆的周长:围成圆的曲线的长叫作圆的周长。
2.圆的周长与直径的关系:圆的周长与圆的直径有关,圆的直径越长,圆的周长就越长。
3.圆周率:任何一个圆的周长除以它的直径的商都是一个固定的数,我们把它叫作圆周率,用字母π表示。
4.π是一个无限不循环小数。π=3.141592653…在计算时,一般保留两位小数,取它的近似值3.14。
5.圆的周长公式:如果用C表示圆的周长,那么周长C与直径d或半径r的关系是:C=πd或C=2πr。
二、考点梳理
知识点④ 已知圆的周长,求直径或半径
解决“已知圆的周长,求直径或半径”的问题时,关键要清楚圆的周长计算公式,
可以列方程解答,也可以用算术方法解答。
二、考点梳理
知识点⑤ 圆的面积
如果用S表示圆的面积,那么圆的面积公式用字母表示是S=πr2。
应用圆的面积公式解决问题时,关键是先找准或求出圆的半径,然后应用圆的面积
公式S=πr2求出圆的面积。
二、考点梳理
知识点⑥ 已知圆的周长求圆的面积
已知圆的周长求圆的面积,要先求出圆的半径,再求圆的面积。
二、考点梳理
知识点⑦ 简单组合图形的面积
1.两个半径不相等的同心圆之间的部分叫作圆环,也叫环形。
2.圆环的面积=外圆的面积-内圆的面积,如果用R表示外圆半径,r表示内圆半径,S表示圆环的面积,那么圆环的面积计算公式是S=πR2-πr2或S=π(R2-r2)。
3.组合图形面积的求法:把图形进行分割、拼接,转化为规则几何图形,再求面积。
三、典例精讲
分析
典例01
根据图示,圆的半径是1厘米,根据
圆的周长公式C=2πr求出圆的周长,
结合题意解答即可。
圆的认识、性质、圆周率及画圆
考点01
解答
解:2×3.14×1=6.28(厘米)
答:M点的位置在6和7之间。因为圆的半径是1厘米,把圆在直尺上无
滑动地滚一周后,滚动的距离是6.28厘米。
故答案为:6;7。
点评
本题考查了圆的周长公式的灵活运用
知识,结合题意解答即可。
如图,M是圆上一点,把圆在直尺上无滑动地滚一周后,M点的位置一
定在 cm和 cm之间,你的理由是什么?
三、典例精讲
分析
变式①
因为圆周长是360度,所以以半圆为
弧的扇形的圆心角是圆周角的一半,
已知扇形的圆心角是90度,用90度
除以360度即可得解。
圆的认识、性质、圆周率及画圆
考点01
解答
点评
本题考查了圆心角的认识,掌握圆心
角的意义是解答题目的关键。
以半圆为弧的扇形的圆心角是 度;以 圆为弧的扇形的
圆心角是90度。
解:360÷2=180(度)
90÷360=
答:以半圆为弧的扇形的圆心角是180度;以 圆为弧的扇形的圆心角
是90度。
故答案为:180; 。
三、典例精讲
分析
变式②
根据图示可知,长方形的长是由1一
个大圆的直径和一个小圆的直径组成,
大圆的直径与长方形的宽相等,据此
利用长减去宽即可求出小圆的直径,
再除以2就是小圆半径;求出两个圆
的直径差再除以大圆的直径即可解答
第二个问题。
圆的认识、性质、圆周率及画圆
考点01
如图所示,长方形的长是5cm,宽是3cm,小圆半径是 cm,小
圆的直径长度比大圆的直径长度少 。
三、典例精讲
点评
解答
解答此题的关键是理解两个圆与长方
形的关系。
圆的认识、性质、圆周率及画圆
考点01
解:5﹣3=2(厘米)
2÷2=1(厘米)
(3﹣2)÷3
=1÷3
=
答:小圆半径是1cm,小圆的直径长度比大圆的直径长度少 。
故答案为:1, 。
三、典例精讲
分析
变式③
根据“直径=半径×2”,代入数字,
求出直径;圆心用字母“o”表示;
半径用字母“r”表示;直径用字母
“d”表示.
用圆规画一个半径是2cm的圆,并用字母标出它的圆心、半径和直径.
圆的认识、性质、圆周率及画圆
考点01
解答
点评
此类题只要先根据圆中直径和半径的
关系,求出直径,然后根据半径即可
画出圆.
解:直径=2×2=4(厘米);
作图如下:
三、典例精讲
分析
典例02
扇形的认识
考点02
如图 ,钟面的分针从“12”走到“3”,形成的以 圆
为弧的扇形的圆心角是 度;钟面的分针从“3”走到“9”,形
成的以 圆为弧的扇形的圆心角是180°。
一个圆的圆心角是360度,钟面的分
针从“12”走到“3”,形成的以
圆为弧的扇形,利用360度除以4即
可求出圆心角的度数;同理解答第二
题。
三、典例精讲
点评
解答
本题考查了扇形的认识。
扇形的认识
考点02
解:360°÷4=90°
180
因此钟面的分针从“12”走到“3”,形成的以 圆为弧的扇形的圆心
角是90度;钟面的分针从“3”走到“9”,形成的以 圆为弧的扇形
的圆心角是180°。
故答案为:90, 。
三、典例精讲
分析
变式①
扇形是一条圆弧和经过这条圆弧两端
的两条半径所围成的图形。先判断,
再用量角器量出圆心角即可。
扇形的认识
考点02
解答
点评
此题考查了扇形的定义,要熟练掌握。
观察如图中的阴影部分。是扇形的标出它的圆心角,不是扇形的在图形
下面对应的括号内画“×”。
解:
三、典例精讲
分析
变式②
一条弧和经过这条弧两端的两条半径
所围成的图形叫扇形做扇形,据此判
断即可。
扇形的认识
考点02
解答
解:根据扇形的定义,只有第一个图和第五个图涂色部分是扇形。
点评
此题主要考查扇形的认识。
如图涂色部分是扇形吗?
三、典例精讲
分析
变式③
根据扇形的意义,一条弧和经过这条
弧两端的两条半径所围成的图形叫扇
形,然后结合图示写出每个扇形的圆
心角和半径即可。
扇形的认识
考点02
解答
点评
此题是考查扇形的意义,然后结合图
示写出每个扇形的圆心角和半径即可。
写出下面每个扇形(涂色部分)的圆心角和半径。
解:解答如下:
三、典例精讲
分析
典例03
(1)小路的面积等于半径为(6÷2+2)米的圆的面积,减去半径是(6÷2)米的圆的面积,利用圆的面积=3.14×半径×半径,结合题中数据计算即可;
(2)需要水泥的重量=小路的面积×每平方米路用水泥重量,由此列式计算即可。
圆、圆环的周长和面积
考点03
为美化校园环境,学校准备在直径是6米的圆形花坛外围铺一条2米宽的
环形小路(如图)。
(1)这条环形小路的面积是多少平方米?
(2)如果铺每平方米路用水泥15千克,铺这条小路一共需要水泥多少
千克?
三、典例精讲
点评
解答
本题考查的是圆的面积公式的应用。
解:(1)6÷2=3(米)
3.14×(3+2)×(3+2)﹣3.14×3×3
=78.5﹣28.26
=50.24(平方米)
答:小路的面积是50.24平方米。
(2)50.24×15=753.6(千克)
答:铺这条小路一共需要水泥753.6千克。
圆、圆环的周长和面积
考点03
三、典例精讲
分析
变式①
利用圆环面积公式:S=π(R2﹣r2)
计算即可。
圆、圆环的周长和面积
考点03
解答
解:3.14×(72﹣42)
=3.14×33
=103.62(平方厘米)
答:阴影部分的面积是103.62平方厘米。
点评
本题主要考查圆环面积公式的应用。
计算阴影部分的面积。(单位:厘米)
三、典例精讲
分析
变式②
根据圆的周长公式:C=2πr,据此
求出油桶一周的长度,然后用A点到
B点的距离除以油桶一周的长度即可
求解。
圆、圆环的周长和面积
考点03
解答
解:2×3.14×0.5
=6.28×0.5
=3.14(米)
6.28÷3.14=2(周)
答:油桶需要滚动2周。
点评
本题考查的是圆形周长计算公式的运
用,熟记公式是解答本题的关键。
张师傅想把一个圆柱形油桶从A点滚到B点(如图),油桶需要滚动几周?
三、典例精讲
分析
变式③
阴影部分的周长=直径是12cm圆的
周长的一半+直径是8cm圆的周长一
半+大圆直径12cm与小圆直径8cm
的差;根据圆的周长公式:周长=
π×直径,代入数据,即可解答。
圆、圆环的周长和面积
考点03
解答
解:3.14×12÷2+3.14×8÷2+(12﹣8)
=3.14×6+3.14×4+4
=18.84+12.56+4
=31.4+4
=35.4(cm)
答:阴影部分的周长是35.4cm。
点评
解答本题需准确分析阴影部分周长的
组成,熟练掌握圆的周长公式。
计算下面图形阴影部分的周长。
谢谢观看~
第六单元 圆
五年级下册 苏教版
一、知识导图
二、考点梳理
知识点① 圆的认识
1.圆是由曲线围成的封闭图形。
2.用圆规画圆时,针尖固定的一点是圆心,连接圆心和圆上任意一点的线段是半径,通过圆心并且两端都在圆上的线段是直径。
3.圆有无数条直径和半径。在同圆或等圆中,直径的长度是半径的2倍,半径的长度是直径的一半,用字母表示为d=2r或r= 。
4.圆是轴对称图形,有无数条对称轴。
二、考点梳理
知识点② 扇形的认识
1.扇形:一条弧和经过这条弧两端点的两条半径所围成的图形叫作扇形。
2.扇形的大小:在同圆或等圆中,扇形的大小与圆心角的大小有关,圆心角大的扇形大,圆心角小的扇形小。
二、考点梳理
知识点③ 圆的周长
1.圆的周长:围成圆的曲线的长叫作圆的周长。
2.圆的周长与直径的关系:圆的周长与圆的直径有关,圆的直径越长,圆的周长就越长。
3.圆周率:任何一个圆的周长除以它的直径的商都是一个固定的数,我们把它叫作圆周率,用字母π表示。
4.π是一个无限不循环小数。π=3.141592653…在计算时,一般保留两位小数,取它的近似值3.14。
5.圆的周长公式:如果用C表示圆的周长,那么周长C与直径d或半径r的关系是:C=πd或C=2πr。
二、考点梳理
知识点④ 已知圆的周长,求直径或半径
解决“已知圆的周长,求直径或半径”的问题时,关键要清楚圆的周长计算公式,
可以列方程解答,也可以用算术方法解答。
二、考点梳理
知识点⑤ 圆的面积
如果用S表示圆的面积,那么圆的面积公式用字母表示是S=πr2。
应用圆的面积公式解决问题时,关键是先找准或求出圆的半径,然后应用圆的面积
公式S=πr2求出圆的面积。
二、考点梳理
知识点⑥ 已知圆的周长求圆的面积
已知圆的周长求圆的面积,要先求出圆的半径,再求圆的面积。
二、考点梳理
知识点⑦ 简单组合图形的面积
1.两个半径不相等的同心圆之间的部分叫作圆环,也叫环形。
2.圆环的面积=外圆的面积-内圆的面积,如果用R表示外圆半径,r表示内圆半径,S表示圆环的面积,那么圆环的面积计算公式是S=πR2-πr2或S=π(R2-r2)。
3.组合图形面积的求法:把图形进行分割、拼接,转化为规则几何图形,再求面积。
三、典例精讲
分析
典例01
根据图示,圆的半径是1厘米,根据
圆的周长公式C=2πr求出圆的周长,
结合题意解答即可。
圆的认识、性质、圆周率及画圆
考点01
解答
解:2×3.14×1=6.28(厘米)
答:M点的位置在6和7之间。因为圆的半径是1厘米,把圆在直尺上无
滑动地滚一周后,滚动的距离是6.28厘米。
故答案为:6;7。
点评
本题考查了圆的周长公式的灵活运用
知识,结合题意解答即可。
如图,M是圆上一点,把圆在直尺上无滑动地滚一周后,M点的位置一
定在 cm和 cm之间,你的理由是什么?
三、典例精讲
分析
变式①
因为圆周长是360度,所以以半圆为
弧的扇形的圆心角是圆周角的一半,
已知扇形的圆心角是90度,用90度
除以360度即可得解。
圆的认识、性质、圆周率及画圆
考点01
解答
点评
本题考查了圆心角的认识,掌握圆心
角的意义是解答题目的关键。
以半圆为弧的扇形的圆心角是 度;以 圆为弧的扇形的
圆心角是90度。
解:360÷2=180(度)
90÷360=
答:以半圆为弧的扇形的圆心角是180度;以 圆为弧的扇形的圆心角
是90度。
故答案为:180; 。
三、典例精讲
分析
变式②
根据图示可知,长方形的长是由1一
个大圆的直径和一个小圆的直径组成,
大圆的直径与长方形的宽相等,据此
利用长减去宽即可求出小圆的直径,
再除以2就是小圆半径;求出两个圆
的直径差再除以大圆的直径即可解答
第二个问题。
圆的认识、性质、圆周率及画圆
考点01
如图所示,长方形的长是5cm,宽是3cm,小圆半径是 cm,小
圆的直径长度比大圆的直径长度少 。
三、典例精讲
点评
解答
解答此题的关键是理解两个圆与长方
形的关系。
圆的认识、性质、圆周率及画圆
考点01
解:5﹣3=2(厘米)
2÷2=1(厘米)
(3﹣2)÷3
=1÷3
=
答:小圆半径是1cm,小圆的直径长度比大圆的直径长度少 。
故答案为:1, 。
三、典例精讲
分析
变式③
根据“直径=半径×2”,代入数字,
求出直径;圆心用字母“o”表示;
半径用字母“r”表示;直径用字母
“d”表示.
用圆规画一个半径是2cm的圆,并用字母标出它的圆心、半径和直径.
圆的认识、性质、圆周率及画圆
考点01
解答
点评
此类题只要先根据圆中直径和半径的
关系,求出直径,然后根据半径即可
画出圆.
解:直径=2×2=4(厘米);
作图如下:
三、典例精讲
分析
典例02
扇形的认识
考点02
如图 ,钟面的分针从“12”走到“3”,形成的以 圆
为弧的扇形的圆心角是 度;钟面的分针从“3”走到“9”,形
成的以 圆为弧的扇形的圆心角是180°。
一个圆的圆心角是360度,钟面的分
针从“12”走到“3”,形成的以
圆为弧的扇形,利用360度除以4即
可求出圆心角的度数;同理解答第二
题。
三、典例精讲
点评
解答
本题考查了扇形的认识。
扇形的认识
考点02
解:360°÷4=90°
180
因此钟面的分针从“12”走到“3”,形成的以 圆为弧的扇形的圆心
角是90度;钟面的分针从“3”走到“9”,形成的以 圆为弧的扇形
的圆心角是180°。
故答案为:90, 。
三、典例精讲
分析
变式①
扇形是一条圆弧和经过这条圆弧两端
的两条半径所围成的图形。先判断,
再用量角器量出圆心角即可。
扇形的认识
考点02
解答
点评
此题考查了扇形的定义,要熟练掌握。
观察如图中的阴影部分。是扇形的标出它的圆心角,不是扇形的在图形
下面对应的括号内画“×”。
解:
三、典例精讲
分析
变式②
一条弧和经过这条弧两端的两条半径
所围成的图形叫扇形做扇形,据此判
断即可。
扇形的认识
考点02
解答
解:根据扇形的定义,只有第一个图和第五个图涂色部分是扇形。
点评
此题主要考查扇形的认识。
如图涂色部分是扇形吗?
三、典例精讲
分析
变式③
根据扇形的意义,一条弧和经过这条
弧两端的两条半径所围成的图形叫扇
形,然后结合图示写出每个扇形的圆
心角和半径即可。
扇形的认识
考点02
解答
点评
此题是考查扇形的意义,然后结合图
示写出每个扇形的圆心角和半径即可。
写出下面每个扇形(涂色部分)的圆心角和半径。
解:解答如下:
三、典例精讲
分析
典例03
(1)小路的面积等于半径为(6÷2+2)米的圆的面积,减去半径是(6÷2)米的圆的面积,利用圆的面积=3.14×半径×半径,结合题中数据计算即可;
(2)需要水泥的重量=小路的面积×每平方米路用水泥重量,由此列式计算即可。
圆、圆环的周长和面积
考点03
为美化校园环境,学校准备在直径是6米的圆形花坛外围铺一条2米宽的
环形小路(如图)。
(1)这条环形小路的面积是多少平方米?
(2)如果铺每平方米路用水泥15千克,铺这条小路一共需要水泥多少
千克?
三、典例精讲
点评
解答
本题考查的是圆的面积公式的应用。
解:(1)6÷2=3(米)
3.14×(3+2)×(3+2)﹣3.14×3×3
=78.5﹣28.26
=50.24(平方米)
答:小路的面积是50.24平方米。
(2)50.24×15=753.6(千克)
答:铺这条小路一共需要水泥753.6千克。
圆、圆环的周长和面积
考点03
三、典例精讲
分析
变式①
利用圆环面积公式:S=π(R2﹣r2)
计算即可。
圆、圆环的周长和面积
考点03
解答
解:3.14×(72﹣42)
=3.14×33
=103.62(平方厘米)
答:阴影部分的面积是103.62平方厘米。
点评
本题主要考查圆环面积公式的应用。
计算阴影部分的面积。(单位:厘米)
三、典例精讲
分析
变式②
根据圆的周长公式:C=2πr,据此
求出油桶一周的长度,然后用A点到
B点的距离除以油桶一周的长度即可
求解。
圆、圆环的周长和面积
考点03
解答
解:2×3.14×0.5
=6.28×0.5
=3.14(米)
6.28÷3.14=2(周)
答:油桶需要滚动2周。
点评
本题考查的是圆形周长计算公式的运
用,熟记公式是解答本题的关键。
张师傅想把一个圆柱形油桶从A点滚到B点(如图),油桶需要滚动几周?
三、典例精讲
分析
变式③
阴影部分的周长=直径是12cm圆的
周长的一半+直径是8cm圆的周长一
半+大圆直径12cm与小圆直径8cm
的差;根据圆的周长公式:周长=
π×直径,代入数据,即可解答。
圆、圆环的周长和面积
考点03
解答
解:3.14×12÷2+3.14×8÷2+(12﹣8)
=3.14×6+3.14×4+4
=18.84+12.56+4
=31.4+4
=35.4(cm)
答:阴影部分的周长是35.4cm。
点评
解答本题需准确分析阴影部分周长的
组成,熟练掌握圆的周长公式。
计算下面图形阴影部分的周长。
谢谢观看~
