第六单元 正比例和反比例(复习课件)-六年级数学下学期期末核心考点集训(苏教版)(共25张PPT)
文档属性
| 名称 | 第六单元 正比例和反比例(复习课件)-六年级数学下学期期末核心考点集训(苏教版)(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 11:18:38 | ||
图片预览








文档简介
(共25张PPT)
第六单元 正比例和反比例
六年级下册 苏教版
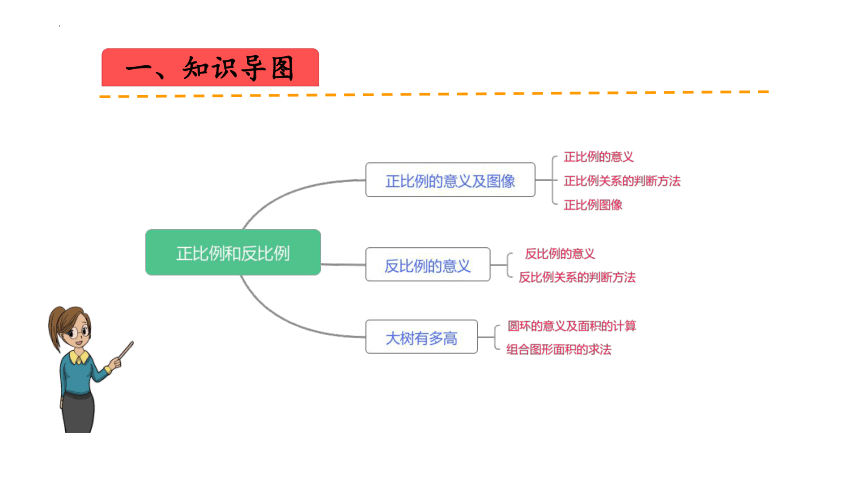
一、知识导图
二、考点梳理
知识点① 正比例的意义及图像
1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化。如果这两
种量中相对应的两个数的比值(也就是商)一定,这两种量就是成正比例的量,它们的
关系就叫作成正比例关系。
2.正比例关系的判断方法:首先判断这两种量是不是相关联的量。再看这两种量相
对应的两个数的比值是否一定,比值一定,则这两种相关联的量成正比例,反之,
则不成正比例。
3.正比例图像:正比例图像是一条经过原点的直线。从图像中可以直观地看出两种
量的变化情况,由一种量的值可以直接找到对应的另一种量的值。
二、考点梳理
知识点② 反比例的意义
1.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两
种量中相对应的两个数的积一定,这两种量就是成反比例的量,它们的关系就叫反
比例关系。
2.反比例关系的判断方法:(1)两种量是相关联的量,一种量变化,另一种量也随着
变化。(2)两种量中相对应的两个数的积一定。
二、考点梳理
知识点③ 大树有多高
1.在外通过测量各种物体的长度及其影子的长度,然后再找出物体长度和影子的比例关系,找出其中的规律。
2.在活动过程中积累数学活动的基本经验,仔细感受解决问题的乐趣,感受数学在实际生活中的应用。
3.以分组的形式,培养自己解决问题的能力以及团队合作精神和创新意识。
三、典例精讲
分析
典例01
(1)先用100×6,求出果汁的总量,再用果汁的总量除以分的杯数4即可;
(2)果汁的总量一定,分的杯数变化,每杯果汁量也随着变化,杯数缩小,每杯果汁量反而扩大,杯数扩大,每杯果汁量反而缩小,而且每两个相对应的数的乘积都是600,所以,果汁的总量一定,杯数和每杯果汁量成反比例;
(3)用果汁的总量600除以杯数10即可.
把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如表.
(1)请把上表补充完整.
(2)分的杯数和每杯的果汁量有什么关系?为什么?
(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?
正比例和反比例的意义
考点01
分的杯数/杯 6 5 4 3
每杯的果汁量/mL 100 120 200
三、典例精讲
点评
解答
本题主要考查了反比例的意义:即两
种相关联的量,一种量变化,另一种
量也随着变化,这两种量中相对应的
两个数的积一定这两种量叫做成反比
例的量.
解:(1)100×6÷4
=600÷4
=150(mL)
填表如下:
(2)分的杯数和每杯的果汁量成反比例.因为总量一定,每杯果汁量
随着分的杯数的变化而变化;杯数增加,每杯果汁量反而减少;杯数减
少,每杯果汁量反而增加,而 杯数与每杯果汁量的乘积一定.
(3)600÷10=60(mL)
答:如果把这些果汁平均分成10杯,每杯的果汁量是60毫升.
故答案为:150.
正比例和反比例的意义
考点01
分的杯数/杯 6 5 4 3
每杯的果汁量/mL 100 120 150 200
三、典例精讲
分析
变式①
根据x和y两个量成反比例关系,可知
x和y这两个量对应的乘积一定,进而
根据乘积一定计算解答即可。
根据如表中x和y两个量的前几组关系,把表格补充完整。
如表x和y两个量的关系可以用式子 表示。
正比例和反比例的意义
考点01
解答
解:4×15=60,10×6=60,300×0.2=60
60÷6=10
60÷0.5=120
60÷2=30
x和y两个量的关系可以用式子xy=60表示。
故答案为:xy=60。
点评
此题属于考查正、反比例的意义,如
果两种相关联的量成反比例关系,那
么它们对应的乘积一定相等。
x 4 10 300 6 2
y 15 6 0.2 0.5
x 4 10 300 6 120 2
y 15 6 0.2 10 0.5 30
三、典例精讲
分析
变式②
(1)看图即可找出800千米相对应的时间;
(2)根据正比例的意义和反比例的意义进行解答即可:看两种相关联量成什么比例关系,要看比值一定还是乘积一定,如乘积一定,则两种量成反比例;如比值一定,则两种量成正比例;
(3)因为这列动车行驶的时间和路程成正比例,可设4.5小时行驶x千米,列比例式为x:4.5=200:1,解答即可.
正比例和反比例的意义
考点01
一列动车在高速铁路上行驶的时间和路程如图.看图填写:
(1)这列动车行800千米需要 小时.
(2)这列动车行驶的时间和路程成 比例.
(3)照这样计算,4.5小时行驶 千米.
三、典例精讲
点评
解答
解答此题的关键是:看两种相关联量
成什么比例关系,要看比值一定还是
乘积一定,如乘积一定,则两种量成
反比例;如比值一定,则两种量成正
比例;同时考查了分析统计图以及据
此解决问题的能力.
解:(1)这列动车行800千米需要4小时.
(2)400÷2=200,800÷4=200,…
因为;行驶的路程与时间的比值一定,
所以:这列动车行驶的时间和路程成正比例.
(3)设4.5小时行驶x千米,
x:4.5=200:1
2x=4.5×400
x=900
答:4.5小时行驶900千米.
故答案为:4,正,900.
正比例和反比例的意义
考点01
三、典例精讲
分析
变式③
(1)先求出甲车行驶的时间,再根据速度=路程÷时间,列式解答。
(2)根据乙的行车轨迹,可以知道路程和时间成正比例关系,因为路程是随着时间的变化而变化。
正比例和反比例的意义
考点01
甲乙两车从A地开往B地,在同一条公路上行驶,情况如图所示。
(1)甲车先慢后快,它的平均速度是每小时多少千米?
(2)根据乙的行车轨迹,可以知道哪两种量存在怎样的比例关系?为
什么?
三、典例精讲
点评
解答
此题考查了行程问题的知识,解题的
关键是知道速度=路程÷时间,要求
学生掌握。
解:(1)9:30﹣7:00=2:30
2时30分=2.5小时
180÷2.5=72(千米/时)
答:它的平均速度是每小时72千米。
(2)根据乙的行车轨迹,可以知道路程和时间成正比例关系,因为路
程是随着时间的变化而变化。
正比例和反比例的意义
考点01
三、典例精讲
分析
典例02
(1)总价随着数量的增多而变大;
(2)分别求出总价与数量之间的关系,是比值一定,成正比例;
(3)描出表示总价和相对应数量的点,然后把它们按顺序连起来即可;
(4)根据单价×数量=总价进行解答。
蓝田是伏羲和女娲的母亲,炎帝和黄帝的直系远祖华胥的故里,四大名
玉之一蓝田玉的原产地。某玉器店售出一种蓝田玉手镯的数量与总价的
关系如下表。
(1)总价是怎样随着数量的变化而变化的?
(2)该玉器店售出这种蓝田玉手镯的总价与数量成正比例关系吗?为什么?
(3)在图中描出表示总价和相对应数量的点,然后把它们按顺序连起来。
(4)该玉器店售出7个这种蓝田玉手镯的总价是 元。
辨识成正比例的量与成反比例的量
考点02
数量/个 0 1 2 3 4 5 6 …
总价/元 0 150 300 450 600 750 900 …
三、典例精讲
点评
解答
此题主要考查正比例的意义以及总价、
数量和单价之间的关系的运用。
辨识成正比例的量与成反比例的量
考点02
解:(1)观察表格可知,总价随着数量的增多而变大;
(2)150÷1=150,300÷2=150,450÷3=150
600÷4=150,750÷5=150,900÷6=150
因为,总价÷数量=单价(一定),该玉器店售出这种蓝田玉手镯的总
价与数量成正比例。
(3)画图如下:
(4)150×7=1050(元)
答:该玉器店售出7个这种蓝田玉手镯的总价是1050元。
故答案为:1050。
三、典例精讲
分析
变式①
(1)用奖品数与总钱数相除,看商是不是不变的,如果商不变那么这两个量成正比例;
(2)根据所给数据画图即可。
如表是李老师在数学周购买奖品时记录的奖品数与总钱数的相关数据。
(1)奖品数和总钱数成 比例。
(2)根据表中的数据,在图中描出相对应的点,再连接起来。
辨识成正比例的量与成反比例的量
考点02
奖品数/个 50 100 150 200 250 ……
总钱数/元 200 400 600 800 1000 ……
三、典例精讲
点评
解答
本题考查的是辨识正反比例,关键是
看这两种相关量中相对应的两个数是
商一定还是积一定,如果商一定,就
成正比例;如果积一定,就成反比例。
辨识成正比例的量与成反比例的量
考点02
解:(1)200÷50=4(元),400÷100=4(元),600÷150=4
(元)......奖品的总钱数÷奖品的个数=4(一定),所以奖品数和总钱
数成正比例;
(2)
故答案为:正。
三、典例精讲
分析
变式②
(1)分别计算出水费与用水量的比值,再根据计算结果判断,如果比值一定,则水费与用水量成正比例;
(2)根据水费与用水量的比值一定,用所求的比值乘用水量即可求出水费。
如表所示是和平里小区22号楼1单元6个住户6月份的用水量情况统计表。
(1)水费和用水量成什么比例?说明理由。
(2)根据水费和用水量的关系,将表格填完整。
辨识成正比例的量与成反比例的量
考点02
住户 101 201 301 401 501 601
用水量(吨) 8 6 9 5 10 7
水费(元) 36 27 40.5 22.5
三、典例精讲
点评
解答
本题考查的是正比例和反比例意义的
运用,掌握正比例和反比例的意义是
解答本题的关键。
解:(1)36:8=4.5
27:6=4.5
40.5:9=4.5
22.5:5=4.5
答:水费与用水量成正比例,因为水费与用水量的比值一定。
(2)10×4.5=45(元)
7×4.5=31.5(元)
辨识成正比例的量与成反比例的量
考点02
住户 101 201 301 401 501 601
用水量(吨) 8 6 9 5 10 7
水费(元) 36 27 40.5 22.5 45 31.5
三、典例精讲
分析
变式③
(1)判断生产的零件数与时间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
(2)先分别求出时间,再比较即可;
(3)问题合理即可。
辨识成正比例的量与成反比例的量
考点02
如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系。
(1)甲车间生产的零件数与时间成正比例吗?为什么?
(2)如果生产8万个零件,那么乙车间比甲车间少用几个月?
(3)根据图象信息,请你提出一个数学问题再解答。
三、典例精讲
点评
解答
本题考查了比例的有关知识,解题的
关键是从折线统计图中得到进一步解
题的相关信息,结合题意分析解答即
可。
解:(1)由图意可知,工作效率=工作总量÷工作时间,工作效率是一
定的,所以甲车间生产的零件数与时间成正比例;
(2)乙生产8万个零件需要:
8÷2=4(个月)
甲生产8万个零件需要:
8÷(2÷2)=8(个月)
8﹣4=4(个月)
答:如果生产8万个零件,那么乙车间比甲车间少用4个月。
(3)乙车间3个月加工多少万个零件?
2×3=6(万)
答:乙车间3个月加工6万个零件。(合理即可,答案不唯一)
辨识成正比例的量与成反比例的量
考点02
三、典例精讲
分析
典例03
根据题意知道,走廊的面积一定,方
砖的面积和方砖的块数成反比例,由
此列式解答即可.
暑假期间,学校准备用方砖铺走廊,如果用面积是9平方分米的方砖,
需要480块,如果用面积是16平方分米的方砖,则至少需要多少块?
(用比例解)
比例的应用
考点03
解答
点评
解答此题的关键是弄清题意,先判断
哪两种相关联的量成何比例,再找准
对应量,列式解答即可.
解:设至少需要x块.
480×9=16x
x=
x=270;
答:至少需要270块.
三、典例精讲
分析
变式①
由题意可知:每天修路的长度是一定
的,即修的路的长度与需要的天数的
比值是一定的,则修的路的长度与需
要的天数成正比例,于是可以列比例
求出21天修的路的长度,进而就能
求出这条公路的总长度.
修一条公路,开工3天修了1.5千米,照这样的速度,再修21天就可以完
成任务,这条公路长多少千米?(用比例解)
比例的应用
考点02
解答
解:设21天修路的长度为x千米,
则有1.5:3=x:21,
3x=21×1.5,
3x=31.5,
x=10.5;
10.5+1.5=12(千米);
答:这条公路长12千米.
点评
此题主要考查利用正比例的意义解决
实际问题,即若两个相关联量的比值
一定,则这两个量成正比例,于是可
以列比例求解.
三、典例精讲
分析
变式②
甲乙两站的路程一定,也就是速度与
时间的乘积一定,时间与速度成反比
例关系.把客车与货车速度分别看成
3和2.设货车行驶x小时到达,可得
方程,解方程即可.
一列客车和一列货车同时从甲乙两站相向开出,客车与货车速度比是3:
2,客车行驶6小时到达乙站,货车行驶多少小时到达甲站?
比例的应用
考点02
解答
解:设货车行驶x小时到达.
2x=3×6
x=18÷2
x=9
答:货车行驶9小时到达.
点评
此题重点考查比例的应用.
三、典例精讲
分析
变式③
把原计划每天铺的长度看作单位
“1”,则实际每天铺[3.2×
(1+25%)]千米;这段铁路的长度
一定,则每天铺的长度与铺的天数成
反比,据此可列比例解答.
一个筑路队铺一段铁路,原计划每天铺3.2千米,实际每天比原计划多铺
25%,实际铺完这段铁路用了12天,原计划用多少天铺完?(用比例解)
比例的应用
考点02
解答
解:设原计划铺x天,
3.2x=3.2×(1+25%)×12,
3.2x=4×12,
3.2x=48,
x=15;
答:原计划用15天铺完.
点评
解答此题的关键是:先求出实际每天
铺的长度,再据这段铁路的长度一定,
则每天铺的长度与铺的天数成反比,
即可列比例求解.
谢谢观看~
第六单元 正比例和反比例
六年级下册 苏教版
一、知识导图
二、考点梳理
知识点① 正比例的意义及图像
1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化。如果这两
种量中相对应的两个数的比值(也就是商)一定,这两种量就是成正比例的量,它们的
关系就叫作成正比例关系。
2.正比例关系的判断方法:首先判断这两种量是不是相关联的量。再看这两种量相
对应的两个数的比值是否一定,比值一定,则这两种相关联的量成正比例,反之,
则不成正比例。
3.正比例图像:正比例图像是一条经过原点的直线。从图像中可以直观地看出两种
量的变化情况,由一种量的值可以直接找到对应的另一种量的值。
二、考点梳理
知识点② 反比例的意义
1.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两
种量中相对应的两个数的积一定,这两种量就是成反比例的量,它们的关系就叫反
比例关系。
2.反比例关系的判断方法:(1)两种量是相关联的量,一种量变化,另一种量也随着
变化。(2)两种量中相对应的两个数的积一定。
二、考点梳理
知识点③ 大树有多高
1.在外通过测量各种物体的长度及其影子的长度,然后再找出物体长度和影子的比例关系,找出其中的规律。
2.在活动过程中积累数学活动的基本经验,仔细感受解决问题的乐趣,感受数学在实际生活中的应用。
3.以分组的形式,培养自己解决问题的能力以及团队合作精神和创新意识。
三、典例精讲
分析
典例01
(1)先用100×6,求出果汁的总量,再用果汁的总量除以分的杯数4即可;
(2)果汁的总量一定,分的杯数变化,每杯果汁量也随着变化,杯数缩小,每杯果汁量反而扩大,杯数扩大,每杯果汁量反而缩小,而且每两个相对应的数的乘积都是600,所以,果汁的总量一定,杯数和每杯果汁量成反比例;
(3)用果汁的总量600除以杯数10即可.
把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如表.
(1)请把上表补充完整.
(2)分的杯数和每杯的果汁量有什么关系?为什么?
(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?
正比例和反比例的意义
考点01
分的杯数/杯 6 5 4 3
每杯的果汁量/mL 100 120 200
三、典例精讲
点评
解答
本题主要考查了反比例的意义:即两
种相关联的量,一种量变化,另一种
量也随着变化,这两种量中相对应的
两个数的积一定这两种量叫做成反比
例的量.
解:(1)100×6÷4
=600÷4
=150(mL)
填表如下:
(2)分的杯数和每杯的果汁量成反比例.因为总量一定,每杯果汁量
随着分的杯数的变化而变化;杯数增加,每杯果汁量反而减少;杯数减
少,每杯果汁量反而增加,而 杯数与每杯果汁量的乘积一定.
(3)600÷10=60(mL)
答:如果把这些果汁平均分成10杯,每杯的果汁量是60毫升.
故答案为:150.
正比例和反比例的意义
考点01
分的杯数/杯 6 5 4 3
每杯的果汁量/mL 100 120 150 200
三、典例精讲
分析
变式①
根据x和y两个量成反比例关系,可知
x和y这两个量对应的乘积一定,进而
根据乘积一定计算解答即可。
根据如表中x和y两个量的前几组关系,把表格补充完整。
如表x和y两个量的关系可以用式子 表示。
正比例和反比例的意义
考点01
解答
解:4×15=60,10×6=60,300×0.2=60
60÷6=10
60÷0.5=120
60÷2=30
x和y两个量的关系可以用式子xy=60表示。
故答案为:xy=60。
点评
此题属于考查正、反比例的意义,如
果两种相关联的量成反比例关系,那
么它们对应的乘积一定相等。
x 4 10 300 6 2
y 15 6 0.2 0.5
x 4 10 300 6 120 2
y 15 6 0.2 10 0.5 30
三、典例精讲
分析
变式②
(1)看图即可找出800千米相对应的时间;
(2)根据正比例的意义和反比例的意义进行解答即可:看两种相关联量成什么比例关系,要看比值一定还是乘积一定,如乘积一定,则两种量成反比例;如比值一定,则两种量成正比例;
(3)因为这列动车行驶的时间和路程成正比例,可设4.5小时行驶x千米,列比例式为x:4.5=200:1,解答即可.
正比例和反比例的意义
考点01
一列动车在高速铁路上行驶的时间和路程如图.看图填写:
(1)这列动车行800千米需要 小时.
(2)这列动车行驶的时间和路程成 比例.
(3)照这样计算,4.5小时行驶 千米.
三、典例精讲
点评
解答
解答此题的关键是:看两种相关联量
成什么比例关系,要看比值一定还是
乘积一定,如乘积一定,则两种量成
反比例;如比值一定,则两种量成正
比例;同时考查了分析统计图以及据
此解决问题的能力.
解:(1)这列动车行800千米需要4小时.
(2)400÷2=200,800÷4=200,…
因为;行驶的路程与时间的比值一定,
所以:这列动车行驶的时间和路程成正比例.
(3)设4.5小时行驶x千米,
x:4.5=200:1
2x=4.5×400
x=900
答:4.5小时行驶900千米.
故答案为:4,正,900.
正比例和反比例的意义
考点01
三、典例精讲
分析
变式③
(1)先求出甲车行驶的时间,再根据速度=路程÷时间,列式解答。
(2)根据乙的行车轨迹,可以知道路程和时间成正比例关系,因为路程是随着时间的变化而变化。
正比例和反比例的意义
考点01
甲乙两车从A地开往B地,在同一条公路上行驶,情况如图所示。
(1)甲车先慢后快,它的平均速度是每小时多少千米?
(2)根据乙的行车轨迹,可以知道哪两种量存在怎样的比例关系?为
什么?
三、典例精讲
点评
解答
此题考查了行程问题的知识,解题的
关键是知道速度=路程÷时间,要求
学生掌握。
解:(1)9:30﹣7:00=2:30
2时30分=2.5小时
180÷2.5=72(千米/时)
答:它的平均速度是每小时72千米。
(2)根据乙的行车轨迹,可以知道路程和时间成正比例关系,因为路
程是随着时间的变化而变化。
正比例和反比例的意义
考点01
三、典例精讲
分析
典例02
(1)总价随着数量的增多而变大;
(2)分别求出总价与数量之间的关系,是比值一定,成正比例;
(3)描出表示总价和相对应数量的点,然后把它们按顺序连起来即可;
(4)根据单价×数量=总价进行解答。
蓝田是伏羲和女娲的母亲,炎帝和黄帝的直系远祖华胥的故里,四大名
玉之一蓝田玉的原产地。某玉器店售出一种蓝田玉手镯的数量与总价的
关系如下表。
(1)总价是怎样随着数量的变化而变化的?
(2)该玉器店售出这种蓝田玉手镯的总价与数量成正比例关系吗?为什么?
(3)在图中描出表示总价和相对应数量的点,然后把它们按顺序连起来。
(4)该玉器店售出7个这种蓝田玉手镯的总价是 元。
辨识成正比例的量与成反比例的量
考点02
数量/个 0 1 2 3 4 5 6 …
总价/元 0 150 300 450 600 750 900 …
三、典例精讲
点评
解答
此题主要考查正比例的意义以及总价、
数量和单价之间的关系的运用。
辨识成正比例的量与成反比例的量
考点02
解:(1)观察表格可知,总价随着数量的增多而变大;
(2)150÷1=150,300÷2=150,450÷3=150
600÷4=150,750÷5=150,900÷6=150
因为,总价÷数量=单价(一定),该玉器店售出这种蓝田玉手镯的总
价与数量成正比例。
(3)画图如下:
(4)150×7=1050(元)
答:该玉器店售出7个这种蓝田玉手镯的总价是1050元。
故答案为:1050。
三、典例精讲
分析
变式①
(1)用奖品数与总钱数相除,看商是不是不变的,如果商不变那么这两个量成正比例;
(2)根据所给数据画图即可。
如表是李老师在数学周购买奖品时记录的奖品数与总钱数的相关数据。
(1)奖品数和总钱数成 比例。
(2)根据表中的数据,在图中描出相对应的点,再连接起来。
辨识成正比例的量与成反比例的量
考点02
奖品数/个 50 100 150 200 250 ……
总钱数/元 200 400 600 800 1000 ……
三、典例精讲
点评
解答
本题考查的是辨识正反比例,关键是
看这两种相关量中相对应的两个数是
商一定还是积一定,如果商一定,就
成正比例;如果积一定,就成反比例。
辨识成正比例的量与成反比例的量
考点02
解:(1)200÷50=4(元),400÷100=4(元),600÷150=4
(元)......奖品的总钱数÷奖品的个数=4(一定),所以奖品数和总钱
数成正比例;
(2)
故答案为:正。
三、典例精讲
分析
变式②
(1)分别计算出水费与用水量的比值,再根据计算结果判断,如果比值一定,则水费与用水量成正比例;
(2)根据水费与用水量的比值一定,用所求的比值乘用水量即可求出水费。
如表所示是和平里小区22号楼1单元6个住户6月份的用水量情况统计表。
(1)水费和用水量成什么比例?说明理由。
(2)根据水费和用水量的关系,将表格填完整。
辨识成正比例的量与成反比例的量
考点02
住户 101 201 301 401 501 601
用水量(吨) 8 6 9 5 10 7
水费(元) 36 27 40.5 22.5
三、典例精讲
点评
解答
本题考查的是正比例和反比例意义的
运用,掌握正比例和反比例的意义是
解答本题的关键。
解:(1)36:8=4.5
27:6=4.5
40.5:9=4.5
22.5:5=4.5
答:水费与用水量成正比例,因为水费与用水量的比值一定。
(2)10×4.5=45(元)
7×4.5=31.5(元)
辨识成正比例的量与成反比例的量
考点02
住户 101 201 301 401 501 601
用水量(吨) 8 6 9 5 10 7
水费(元) 36 27 40.5 22.5 45 31.5
三、典例精讲
分析
变式③
(1)判断生产的零件数与时间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
(2)先分别求出时间,再比较即可;
(3)问题合理即可。
辨识成正比例的量与成反比例的量
考点02
如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系。
(1)甲车间生产的零件数与时间成正比例吗?为什么?
(2)如果生产8万个零件,那么乙车间比甲车间少用几个月?
(3)根据图象信息,请你提出一个数学问题再解答。
三、典例精讲
点评
解答
本题考查了比例的有关知识,解题的
关键是从折线统计图中得到进一步解
题的相关信息,结合题意分析解答即
可。
解:(1)由图意可知,工作效率=工作总量÷工作时间,工作效率是一
定的,所以甲车间生产的零件数与时间成正比例;
(2)乙生产8万个零件需要:
8÷2=4(个月)
甲生产8万个零件需要:
8÷(2÷2)=8(个月)
8﹣4=4(个月)
答:如果生产8万个零件,那么乙车间比甲车间少用4个月。
(3)乙车间3个月加工多少万个零件?
2×3=6(万)
答:乙车间3个月加工6万个零件。(合理即可,答案不唯一)
辨识成正比例的量与成反比例的量
考点02
三、典例精讲
分析
典例03
根据题意知道,走廊的面积一定,方
砖的面积和方砖的块数成反比例,由
此列式解答即可.
暑假期间,学校准备用方砖铺走廊,如果用面积是9平方分米的方砖,
需要480块,如果用面积是16平方分米的方砖,则至少需要多少块?
(用比例解)
比例的应用
考点03
解答
点评
解答此题的关键是弄清题意,先判断
哪两种相关联的量成何比例,再找准
对应量,列式解答即可.
解:设至少需要x块.
480×9=16x
x=
x=270;
答:至少需要270块.
三、典例精讲
分析
变式①
由题意可知:每天修路的长度是一定
的,即修的路的长度与需要的天数的
比值是一定的,则修的路的长度与需
要的天数成正比例,于是可以列比例
求出21天修的路的长度,进而就能
求出这条公路的总长度.
修一条公路,开工3天修了1.5千米,照这样的速度,再修21天就可以完
成任务,这条公路长多少千米?(用比例解)
比例的应用
考点02
解答
解:设21天修路的长度为x千米,
则有1.5:3=x:21,
3x=21×1.5,
3x=31.5,
x=10.5;
10.5+1.5=12(千米);
答:这条公路长12千米.
点评
此题主要考查利用正比例的意义解决
实际问题,即若两个相关联量的比值
一定,则这两个量成正比例,于是可
以列比例求解.
三、典例精讲
分析
变式②
甲乙两站的路程一定,也就是速度与
时间的乘积一定,时间与速度成反比
例关系.把客车与货车速度分别看成
3和2.设货车行驶x小时到达,可得
方程,解方程即可.
一列客车和一列货车同时从甲乙两站相向开出,客车与货车速度比是3:
2,客车行驶6小时到达乙站,货车行驶多少小时到达甲站?
比例的应用
考点02
解答
解:设货车行驶x小时到达.
2x=3×6
x=18÷2
x=9
答:货车行驶9小时到达.
点评
此题重点考查比例的应用.
三、典例精讲
分析
变式③
把原计划每天铺的长度看作单位
“1”,则实际每天铺[3.2×
(1+25%)]千米;这段铁路的长度
一定,则每天铺的长度与铺的天数成
反比,据此可列比例解答.
一个筑路队铺一段铁路,原计划每天铺3.2千米,实际每天比原计划多铺
25%,实际铺完这段铁路用了12天,原计划用多少天铺完?(用比例解)
比例的应用
考点02
解答
解:设原计划铺x天,
3.2x=3.2×(1+25%)×12,
3.2x=4×12,
3.2x=48,
x=15;
答:原计划用15天铺完.
点评
解答此题的关键是:先求出实际每天
铺的长度,再据这段铁路的长度一定,
则每天铺的长度与铺的天数成反比,
即可列比例求解.
谢谢观看~
