图形的认识与测量课件(共73张PPT)六年级下册数学人教版
文档属性
| 名称 | 图形的认识与测量课件(共73张PPT)六年级下册数学人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 11:20:49 | ||
图片预览



文档简介
(共73张PPT)
6 整理和复习
2.图形与几何
数学人教版六年级下册
第1课时 平面图形的认识与测量(1)
情境导入
我们学过哪些平面图形和立体图形?你能对学过的图形进行分类吗?
教材第85页
我这样分类,图形可以分成平面图形和立体图形,平面图形可以分成……
我还可以再细分,三角形按角可以分成……
图形
平面图形
立体图形
锐角
三角形
钝角
三角形
直角
三角形
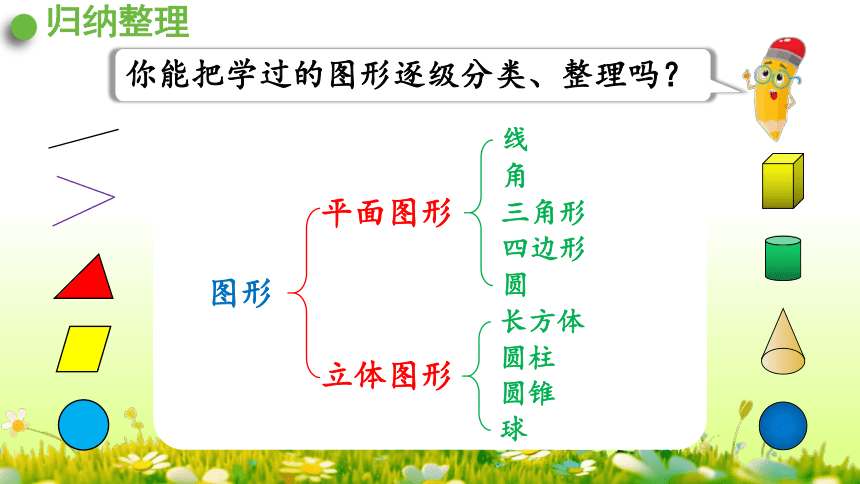
归纳整理
你能把学过的图形逐级分类、整理吗?
图形
平面图形
立体图形
线
角
三角形
圆柱
四边形
圆
圆锥
球
长方体
线
线段、射线、直线
平行线、垂线
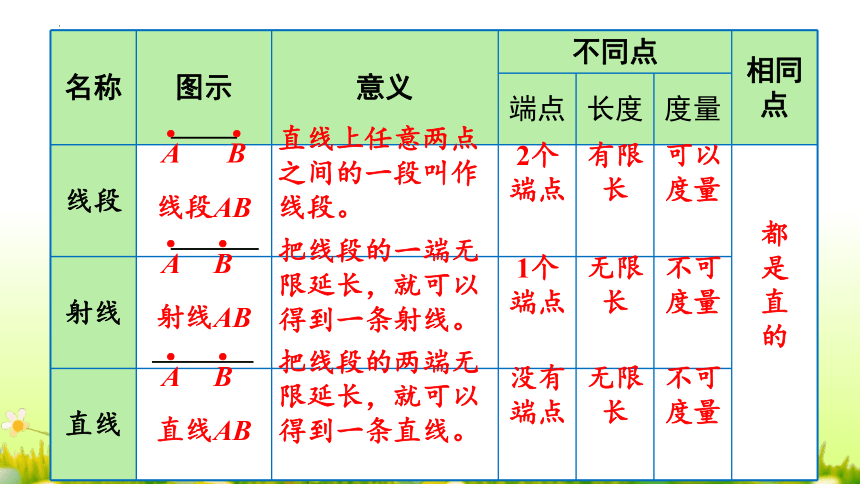
名称 图示 意义 不同点 相同点
端点 长度 度量
线段
射线
直线
直线上任意两点之间的一段叫作线段。
把线段的一端无限延长,就可以得到一条射线。
把线段的两端无限延长,就可以得到一条直线。
2个端点
1个端点
没有端点
有限长
无限长
无限长
可以度量
不可度量
不可度量
都是直的
线段AB
·
A
·
B
射线AB
·
A
·
B
直线AB
·
A
·
B
线
线段、射线、直线
平行线、垂线
位置关系 图示 意义
平行
相交 垂直
不垂直
在同一平面内永不相交的两条直线叫作平行线。
直线a平行于直线b
a
b
a
b
·
P
直线a垂直于直线b
·
两条直线相交成直角,就说明这两条直线互相垂直。其中一条直线叫作另一条直线的垂线。
同一平面内不平行的两条直线一定相交。
垂足
直角符号
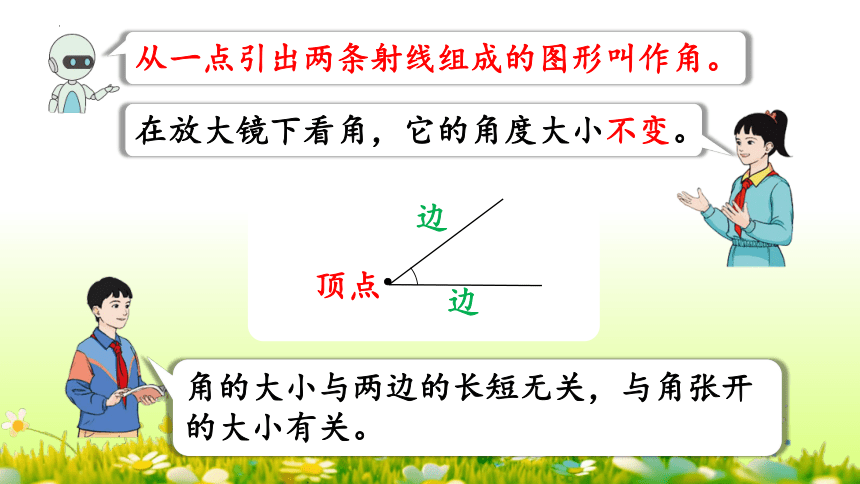
边
顶点
边
角的大小与两边的长短无关,与角张开的大小有关。
·
从一点引出两条射线组成的图形叫作角。
在放大镜下看角,它的角度大小不变。
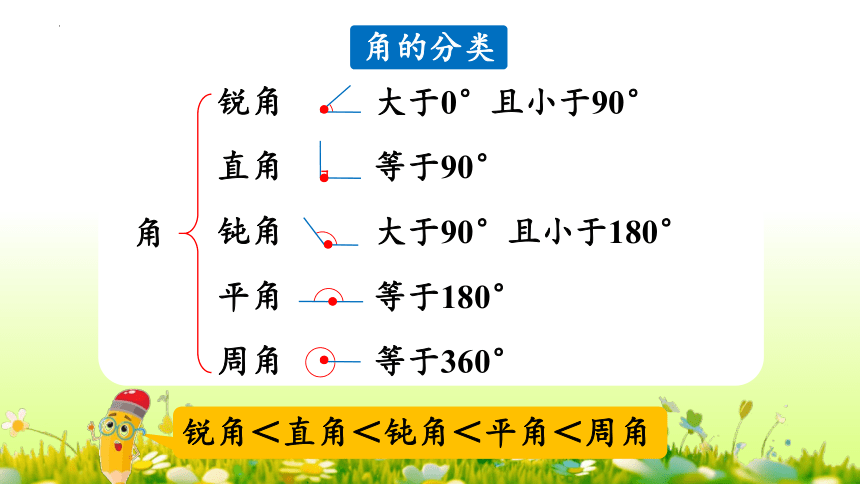
锐角<直角<钝角<平角<周角
角
锐角
钝角
直角
平角
周角
·
·
·
·
·
大于0°且小于90°
等于90°
大于90°且小于180°
等于180°
等于360°
角的分类
边
顶点
边
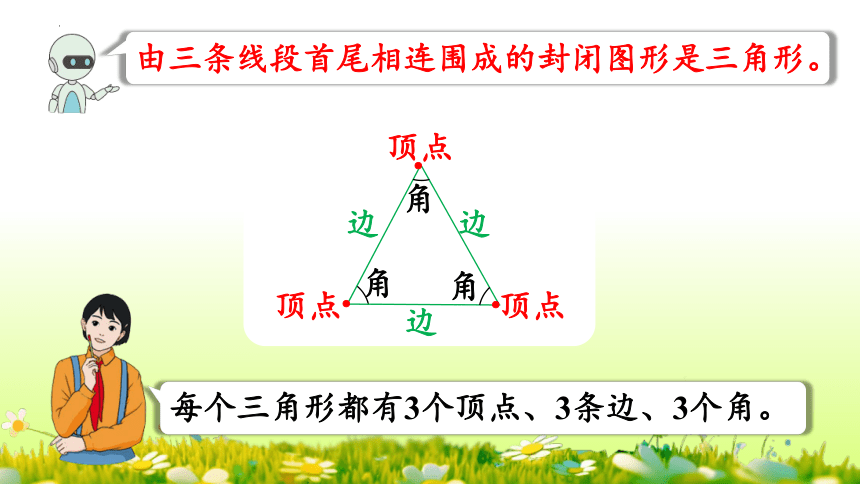
每个三角形都有3个顶点、3条边、3个角。
由三条线段首尾相连围成的封闭图形是三角形。
边
·
·
·
顶点
顶点
角
角
角
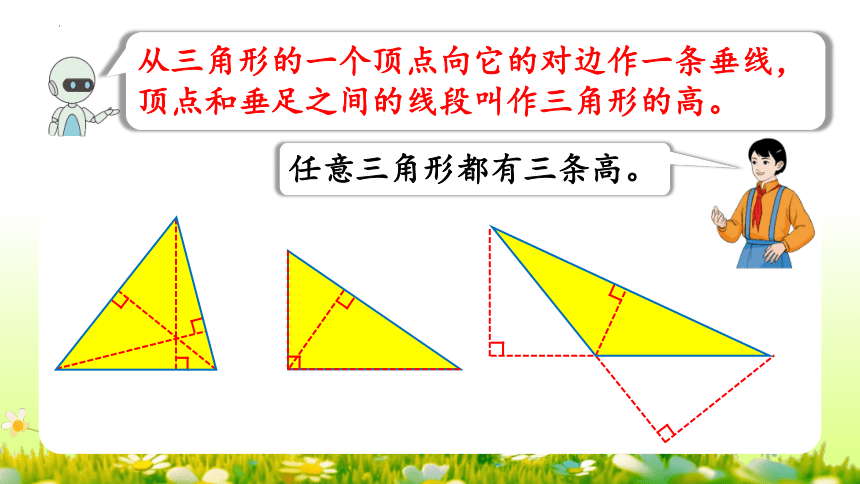
从三角形的一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高。
任意三角形都有三条高。
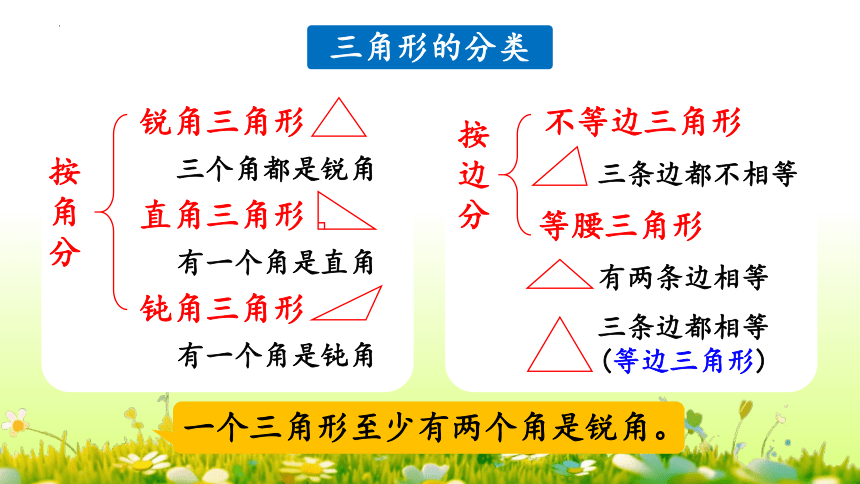
一个三角形至少有两个角是锐角。
按角分
三个角都是锐角
有一个角是直角
有一个角是钝角
三角形的分类
锐角三角形
钝角三角形
直角三角形
按边分
三条边都不相等
有两条边相等
三条边都相等
(等边三角形)
不等边三角形
等腰三角形
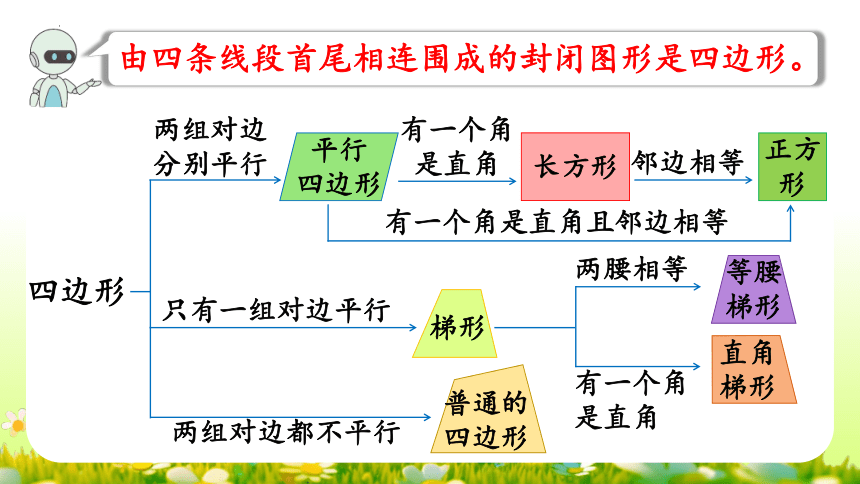
四边形
由四条线段首尾相连围成的封闭图形是四边形。
平行
四边形
梯形
等腰梯形
直角梯形
普通的四边形
长方形
正方形
两组对边分别平行
有一个角是直角
邻边相等
有一个角是直角且邻边相等
只有一组对边平行
两组对边都不平行
两腰相等
有一个角是直角
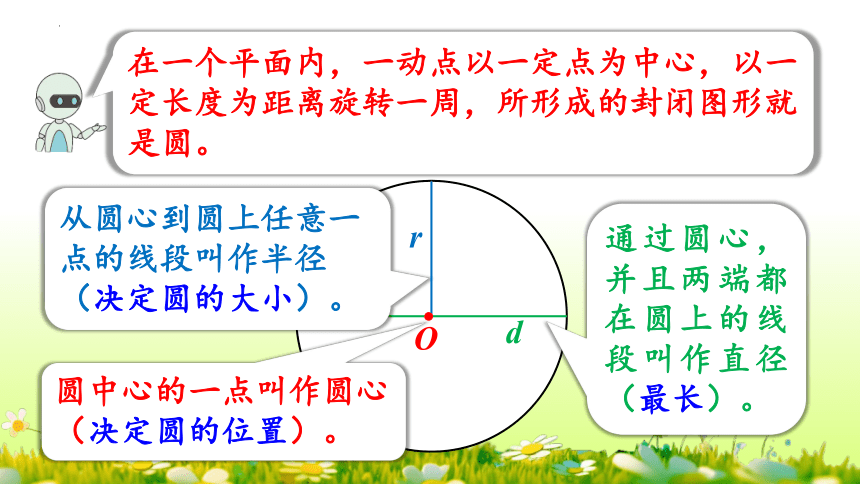
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周,所形成的封闭图形就是圆。
·
O
r
d
圆中心的一点叫作圆心(决定圆的位置)。
从圆心到圆上任意一点的线段叫作半径(决定圆的大小)。
通过圆心,并且两端都在圆上的线段叫作直径(最长)。
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周,所形成的封闭图形就是圆。
两个半径不相等的同心圆之间的部分叫作圆环。
·
O
R
r
外圆
内圆
·
O
一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。
弧
A
B
圆心角
我发现:平行四边形的两组对边、两组对角分别相等。
1.做两个同样的平行四边形纸片。把它们上下重合放置,
将上方的平行四边形绕它的一个顶点旋转180°,再通
过平移使它与另一个平行四边形上下重合。观察两个
平行四边形的各条边与各个角,你有什么发现?
课堂练习
教材第85页“做一做”
2.过一点可以画几条直线?过两点可以画几条直线?
教材第86页“做一做”第1题
答:过一点可以画无数条直线,过两点可以
画一条直线。
3.有长度分别为3 cm、4 cm、 5 cm、 8 cm的小棒各一根 ,哪三根小棒可以围成一个三角形?
教材第86页“做一做”第2题
三角形任意两边之和大于第三边。
3cm、4cm、5cm
4cm、5cm、8cm
4.一个直角三角形的两个锐角的和是多少度?为什么?
教材第86页“做一做”第3题
答:一个直角三角形的两个锐角的和是90°。
因为三角形内角和为180°,180°减去直角90°,就是两个锐角的和90°。
90°
(1)一个三角形三个内角的度数比是2∶3∶5,这个三角形是( )三角形。
5.填一填。
直角
三角形的内角和是180°。
180× =36(度)
2
2+3+5
180× =54(度)
3
2+3+5
180× =90(度)
5
2+3+5
有一个角是直角的三角形是直角三角形。
(2)如果在一个等腰三角形中,有两条边的长度分别是10厘米、4厘米,那么这个等腰三角形的第三条边长是( )厘米。
10
三角形的任意两边之和大于第三边。
等腰三角形有两条边相等。第三条边可能是10厘米,也可能是4厘米。
如果是4厘米,4+4<10,不符合三角形三边关系,所以第三条边是10厘米。
(3)当梯形上底逐渐缩小到一点时,梯形就转化为( )形;当梯形上底增大到与下底相等时,梯形就转化成( )形。
三角
平行四边
(4)如下图,用两个这样的三角形可以拼出( )种不同的平行四边形,其中平行四边形的周长最长的是( )厘米。
5cm
6cm
7cm
5cm
6cm
7cm
5cm
5cm
7cm
7cm
5cm
5cm
6cm
6cm
7cm
7cm
6cm
6cm
3
26
24cm
26cm
22cm
6.判一判。
(1)直线是射线长度的2倍。 ( )
(2)两条直线不平行就相交。 ( )
(3)用放大10倍的放大镜看一个30°的角还是30°。
( )
(4)正方形、平行四边形和圆都是轴对称图形。
( )
×
直线和射线都是无限长,不可以度量。
√
×
“同一平面内”的两条直线不是平行就是相交。
在放大镜下看角,角的大小不变。
平行四边形只有邻边相等或邻角相等时才是轴对称图形。
×
7.选一选。
(1)一个三角形的一部分被一张纸遮住了(如下图),只露出了一个角,这个三角形是( )三角形。
A.锐角 B.直角
C.钝角 D.无法确定
D
(2)如图,下面是用木条钉成的四种支架,最不容易变形的是( )。
C
A
B
C
D
三角形具有稳定性,在生活中应用广泛,如斜拉桥、篮球架等都用到了三角形的稳定性。
(3)将一个正方形剪去一个角,剩下图形的内角和不可能是( )。
A.180° B.360°
C.540° D.720°
D
五边形的内角和是540°
四边形的内角和是360°
三角形的内角和是180°
6 整理和复习
2.图形与几何
数学人教版六年级下册
第2课时 平面图形的认识与测量(2)
问题导入
我们学过哪些平面图形的周长和面积计算公式呢?
教材第86页
这些计算公式是怎样推导出来的?它们之间有什么联系?
a
b
归纳整理
平面图形的面积计算公式
用数方格的方法推导。
把正方形看作长和宽相等的长方形。
a
a
通过割补、平移转化为长方形。
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
把两个完全一样的三角形通过旋转、平移拼成与它们等底等高的平行四边形。三角形的面积等于拼成的平行四边形面积的一半。
平面图形的面积计算公式
三角形的面积=底×高÷2
把两个完全一样的梯形通过旋转、平移拼成一个平行四边形。拼成的平行四边形的底等于梯形的上底与下底的和,高等于梯形的高,所以梯形的面积等于这个平行四边形面积的一半。
平面图形的面积计算公式
梯形的面积=(上底+下底)×高÷2
把一个圆分成若干份,剪拼成一个近似的长方形,这个长方形的长相当于圆周长的一半,宽相当于圆的半径。
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
πr
r
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
三角形的面积=底×高÷2
梯形的面积=(上底+下底)×高÷2
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
平面图形的周长计算公式
圆的周长=圆周率×直径
长方形的周长=(长+宽)×2
正方形的周长=边长×4
平行四边形的周长=相邻两边的长度和×2
三角形的周长=三条边的长度和
梯形的周长=四条边的长度和
C=2(a+b)
C=4a
C=2(a+b)
C=a+b+c
C=a+b+c+d
C=πd=2πr
课堂练习
1.计算下面各图形的周长和面积。(单位:m)
教材第86页“做一做”第4题
周长:
30
40
50
30+40+50=120(m)
面积:
30×40÷2
=1200÷2
=600(m2)
周长:
6×2+10.5+7.5=30(m)
面积:
(6+10.5)×6÷2
=16.5×6÷2
=49.5(m2)
6
7.5
10.5
6
a
b
h
1.计算下面各图形的周长和面积。(单位:m)
3.14×6÷2
1.计算下面各图形的周长和面积。(单位:m)
周长:
=9.42+ 6 +10
=25.42(m)
面积:
=14.13+15
=29.13(m2)
5
3
6
+6
+5×2
3.14×(6÷2)2÷2
+5×3
(1)如下图(单位:cm),一个长方形框架变形后成了一个平行四边形,原来这个长方形的周长是( )cm,变形后的平行四边形面积是( )cm2。
2.填一填。
26
长方形的周长:
8×4=32(cm2)
(8+5)×2=26(cm)
原来长方形的宽为5 cm。
32
8
4
5
5
平行四边形的面积:
(2)如下图的平行四边形中,阴影部分的面积是6cm2,平行四边形的底是直角三角形的3倍,空白部分的面积是( )cm2。
6×2÷4=3(cm)
4 cm
3 cm
三角形的底=面积×2÷高。
3×3=9(cm)
9 cm
9×4-6=30(cm2)
三角形的底:
平行四边形的底:
空白部分的面积:
30
(3)如下图,张大爷用24米长的栅栏靠墙围成一块梯形菜地,这块菜地的面积是( )平方米。
54
6 m
24米长的栅栏分布在梯形的上底、高和下底三个部分,已知高是6米,则上、下底的和是(24-6)米。
(24-6)×6÷2=54(平方米)
(4)在一张长24 cm、宽20 cm的长方形纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2;如果改画最大的半圆,这个半圆的面积( )cm2。
62.8
314
圆的周长:3.14×20=62.8(cm)
圆的面积:3.14×(20÷2)2=314(cm2)
半圆的面积:3.14×(24÷2)2÷2=226.08(cm2)
226.08
圆的直径最大为20 cm。
半圆的直径最大为24 cm。
(5)如图,在大、小两个正方形中涂色部分的面积比是3∶2,则大、小两个正方形的边长比是( ),面积比是( )。
3∶2
9∶4
a
b
b
ab÷2 3
b2÷2 2
=-
-=-
a 3
b 2
涂色部分的面积比:
根据比的基本性质:
a2 32 9
b2 22 4
-=-=-
大、小正方形的面积比:
用a、b分别表示两个正方形的边长。
3.选一选。
(1)一个平行四边形相邻的两条边分别是6 cm、4 cm,量得一条边上的高是5 cm,这个平行四边形的面积是( )cm2。
A.30 B.24 C.20 D.10
C
4 cm
6 cm
小于4 cm
4 cm
4 cm
6 cm
小于6 cm
6 cm
以4 cm为底的高是5 cm
4×5=20(cm2)
(2)一个三角形的底和高相等,如果将底减少2分米,高增加2分米,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
B
原面积:6×6÷2=18(dm2)
新面积:(6-2)×(6+2)÷2=16(dm2)
16<18,面积减少了。
假设原三角形的底和高都是6分米。
(3)如下图,用三张同样大小的正方形纸分别剪掉图中涂色部分的图形,材料的利用率( )。
A.甲最高 B.乙最高 C.丙最高 D.相同
D
甲乙丙
甲:3.14×102÷4÷102=78.5%
乙:3.14×(10÷2)2÷102=78.5%
丙:3.14×(10÷2÷2)2×4÷102=78.5%
假设正方形的边长是10厘米。
(36+52)×42÷2÷1.5
=88×42÷2÷1.5
=1848÷1.5
=1232(棵)
答:这个果园最多可种1232棵果树。
4.一个梯形果园,上底是36米,下底是52米,高是42米。平均每棵果树占地1.5平方米,这个果园最多可种多少棵果树?
梯形的面积=(上底+下底)×高÷2
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
3.14×[(28÷2+2)2-(28÷2)2]
=3.14×[162-142]
=3.14×60
=188.4(平方米)
O
28 m
2 m
圆环的面积:S=π(R2-r2)
2×3.14×(28÷2+2)
=2×3.14×16
=100.48(米)
答:这条道路的面积是188.4平方米,外沿周长是100.48米。
O
外沿的周长:C=2πR
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
28 m
2 m
=3.14×27+3.14×2
=3.14×29
=91.06(平方米)
答:这只羊能吃到草的面积是91.06平方米。
6.草地上有一间房子,占地形状是边长4米的正方形。一只羊被拴在房子的外墙角处,已知栓羊的绳子长6米,这只羊能吃到草的面积是多少平方米?
2 m
6 m
3.14×62×-
3
4
+3.14×(6-4)2×-
1
2
如图,羊能吃到草的面积由三个扇形组成。
答:x的值是11.4。
7.已知下图中两块阴影部分的面积相等,求x的值。
扇形面积:3.14×102÷4=78.5(cm2)
10 cm
O
扇形面积减三角形面积
梯形面积减扇形面积
x cm
(10+x)×10÷2-78.5=78.5-50
三角形面积:10×10÷2=50(cm2)
(10+x)×10÷2=107
10+x=21.4
x=11.4
6 整理和复习
2.图形与几何
数学人教版六年级下册
第3课时 立体图形的认识与测量
情境导入
我们学过哪些立体图形?
它们各有什么特点?
归纳整理
长方体和正方体的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长
长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
教材第87页
圆柱和圆锥的特征
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面圆心之间的距离叫作高,有无数条长度相等的高。
顶点到底面圆心的距离叫作高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
立体图形的表面积计算公式
把长方体沿棱剪开,展开得到6个长方形,长方体的表面积就是这6个长方形的面积和。
长方体的表面积=(长×宽+长×高+宽×高)×2
a
b
h
a
b
h
前
后
左
右
上
下
立体图形的表面积计算公式
把正方体沿棱剪开,展开得到6个完全相同的正方形,正方体的表面积就是其中一个面面积的6倍。
正方体的表面积=棱长的平方×6
a
a
a
a
前
后
左
右
上
下
a
a
立体图形的表面积计算公式
把圆柱沿高和底面圆周剪开,侧面是一个长方形(正方形),圆柱的表面积就是三个面面积的和。
圆柱的表面积=底面积×2+底面周长×高
r
h
C
侧面
上底
下底
h
立体图形的表面积计算公式
圆柱的表面积=底面积×2+底面周长×高
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长的平方×6
圆柱的侧面积=底面周长×高
S=2(ab+ah+bh)
S=6a2
S侧=Ch=πdh=2πrh
S=S侧+2S底=2πrh+2πr2
立体图形的体积计算公式
用棱长为1 cm的小正方体摆成不同的长方体,长方体所含小正方体的数量就是长方体的体积。
长方体的体积=长×宽×高
a
b
h
正方体是长、宽、高都相等的特殊的长方体。
正方体的体积=棱长的立方
a
a
a
立体图形的体积计算公式
把圆柱沿底面直径切成若干等份,可以拼成一个近似的长方体,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高。
圆柱的体积=底面积×高
立体图形的体积计算公式
把圆锥形容器里的水倒入与它等底、等高的圆柱形容器内,3次才能倒满。
圆锥的体积=与圆锥等底、等高的圆柱的体积×-
13
长方体的体积=长×宽×高
正方体的体积=棱长的立方
圆柱的体积=圆周率×半径的平方×高
V=abh
V=a3
V=πr2h
立体图形的体积计算公式
圆锥体积=底面积×高×-
13
V=-S底h=-πr2h
13
13
长方体、正方体、圆柱的体积:V=S底h
课堂练习
1.判断对错,对的画“√”,错的画“×”。
绕着宽所在的直线为轴旋转一周也可以形成圆柱。
(1)长方形只有绕着长所在的直线为轴旋转一周才能形成圆柱。 ( )
(2)任意一个三角形绕它的一条边所在的直线为轴旋转都能形成圆锥。 ( )
(3)体积相等的两个长方体的底面积一定相等。( )
直角三角形绕着直角边所在的直线旋转才能形成圆锥。
×
×
体积是底面积和高的积,高不确定,底面积不一定相等。
×
2.怎样测量出一块拳头大的鹅卵石的体积?
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
求不规则物体体积的方法:
教材第87页“做一做”第1题
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
上升的水的体积就是鹅卵石的体积。
用“底面积×上升的高度”来计算。
2.怎样测量出一块拳头大的鹅卵石的体积?
前面
3.在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
左面
上面
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
教材第87页“做一做”第2题
4.小明用一根铁丝做成一个正方体框架。已知这个正方体框架的一个面的面积是49平方厘米,这根铁丝至少长( )厘米。
84
正方体的每个面都是正方形,因为49=72,所以正方体的棱长为7厘米,铁丝的长度也就是12条棱的长度和,即12×7=84(厘米)。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
22
这个物体的表面由22个正方形围成,每个正方形的面积是1×1=1(平方厘米),所以表面积是20×1=1(平方厘米)。
求表面积可以数一数表面有几个正方形。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
7
拼成的大长方体的长至少是3厘米,宽至少是2厘米,高至少是2厘米,因此一共需要3×2×2=12(个)小正方体,已有5个,至少添加12-5=7(个)。
22
先思考拼成的大长方体一共需要多少个小正方体。
6.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
7.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
8.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
12÷3=4(cm)
9.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,如果把它捏成同样高的一个圆柱,那么该圆柱的底面积是多少平方厘米?
圆锥体积=底面积×高×-
13
12×6×-=24(立方厘米)
13
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
圆锥变成圆柱的过程中,体积不变。
答:该圆柱的底面积是4平方厘米。
Thank you!
6 整理和复习
2.图形与几何
数学人教版六年级下册
第1课时 平面图形的认识与测量(1)
情境导入
我们学过哪些平面图形和立体图形?你能对学过的图形进行分类吗?
教材第85页
我这样分类,图形可以分成平面图形和立体图形,平面图形可以分成……
我还可以再细分,三角形按角可以分成……
图形
平面图形
立体图形
锐角
三角形
钝角
三角形
直角
三角形
归纳整理
你能把学过的图形逐级分类、整理吗?
图形
平面图形
立体图形
线
角
三角形
圆柱
四边形
圆
圆锥
球
长方体
线
线段、射线、直线
平行线、垂线
名称 图示 意义 不同点 相同点
端点 长度 度量
线段
射线
直线
直线上任意两点之间的一段叫作线段。
把线段的一端无限延长,就可以得到一条射线。
把线段的两端无限延长,就可以得到一条直线。
2个端点
1个端点
没有端点
有限长
无限长
无限长
可以度量
不可度量
不可度量
都是直的
线段AB
·
A
·
B
射线AB
·
A
·
B
直线AB
·
A
·
B
线
线段、射线、直线
平行线、垂线
位置关系 图示 意义
平行
相交 垂直
不垂直
在同一平面内永不相交的两条直线叫作平行线。
直线a平行于直线b
a
b
a
b
·
P
直线a垂直于直线b
·
两条直线相交成直角,就说明这两条直线互相垂直。其中一条直线叫作另一条直线的垂线。
同一平面内不平行的两条直线一定相交。
垂足
直角符号
边
顶点
边
角的大小与两边的长短无关,与角张开的大小有关。
·
从一点引出两条射线组成的图形叫作角。
在放大镜下看角,它的角度大小不变。
锐角<直角<钝角<平角<周角
角
锐角
钝角
直角
平角
周角
·
·
·
·
·
大于0°且小于90°
等于90°
大于90°且小于180°
等于180°
等于360°
角的分类
边
顶点
边
每个三角形都有3个顶点、3条边、3个角。
由三条线段首尾相连围成的封闭图形是三角形。
边
·
·
·
顶点
顶点
角
角
角
从三角形的一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高。
任意三角形都有三条高。
一个三角形至少有两个角是锐角。
按角分
三个角都是锐角
有一个角是直角
有一个角是钝角
三角形的分类
锐角三角形
钝角三角形
直角三角形
按边分
三条边都不相等
有两条边相等
三条边都相等
(等边三角形)
不等边三角形
等腰三角形
四边形
由四条线段首尾相连围成的封闭图形是四边形。
平行
四边形
梯形
等腰梯形
直角梯形
普通的四边形
长方形
正方形
两组对边分别平行
有一个角是直角
邻边相等
有一个角是直角且邻边相等
只有一组对边平行
两组对边都不平行
两腰相等
有一个角是直角
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周,所形成的封闭图形就是圆。
·
O
r
d
圆中心的一点叫作圆心(决定圆的位置)。
从圆心到圆上任意一点的线段叫作半径(决定圆的大小)。
通过圆心,并且两端都在圆上的线段叫作直径(最长)。
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周,所形成的封闭图形就是圆。
两个半径不相等的同心圆之间的部分叫作圆环。
·
O
R
r
外圆
内圆
·
O
一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。
弧
A
B
圆心角
我发现:平行四边形的两组对边、两组对角分别相等。
1.做两个同样的平行四边形纸片。把它们上下重合放置,
将上方的平行四边形绕它的一个顶点旋转180°,再通
过平移使它与另一个平行四边形上下重合。观察两个
平行四边形的各条边与各个角,你有什么发现?
课堂练习
教材第85页“做一做”
2.过一点可以画几条直线?过两点可以画几条直线?
教材第86页“做一做”第1题
答:过一点可以画无数条直线,过两点可以
画一条直线。
3.有长度分别为3 cm、4 cm、 5 cm、 8 cm的小棒各一根 ,哪三根小棒可以围成一个三角形?
教材第86页“做一做”第2题
三角形任意两边之和大于第三边。
3cm、4cm、5cm
4cm、5cm、8cm
4.一个直角三角形的两个锐角的和是多少度?为什么?
教材第86页“做一做”第3题
答:一个直角三角形的两个锐角的和是90°。
因为三角形内角和为180°,180°减去直角90°,就是两个锐角的和90°。
90°
(1)一个三角形三个内角的度数比是2∶3∶5,这个三角形是( )三角形。
5.填一填。
直角
三角形的内角和是180°。
180× =36(度)
2
2+3+5
180× =54(度)
3
2+3+5
180× =90(度)
5
2+3+5
有一个角是直角的三角形是直角三角形。
(2)如果在一个等腰三角形中,有两条边的长度分别是10厘米、4厘米,那么这个等腰三角形的第三条边长是( )厘米。
10
三角形的任意两边之和大于第三边。
等腰三角形有两条边相等。第三条边可能是10厘米,也可能是4厘米。
如果是4厘米,4+4<10,不符合三角形三边关系,所以第三条边是10厘米。
(3)当梯形上底逐渐缩小到一点时,梯形就转化为( )形;当梯形上底增大到与下底相等时,梯形就转化成( )形。
三角
平行四边
(4)如下图,用两个这样的三角形可以拼出( )种不同的平行四边形,其中平行四边形的周长最长的是( )厘米。
5cm
6cm
7cm
5cm
6cm
7cm
5cm
5cm
7cm
7cm
5cm
5cm
6cm
6cm
7cm
7cm
6cm
6cm
3
26
24cm
26cm
22cm
6.判一判。
(1)直线是射线长度的2倍。 ( )
(2)两条直线不平行就相交。 ( )
(3)用放大10倍的放大镜看一个30°的角还是30°。
( )
(4)正方形、平行四边形和圆都是轴对称图形。
( )
×
直线和射线都是无限长,不可以度量。
√
×
“同一平面内”的两条直线不是平行就是相交。
在放大镜下看角,角的大小不变。
平行四边形只有邻边相等或邻角相等时才是轴对称图形。
×
7.选一选。
(1)一个三角形的一部分被一张纸遮住了(如下图),只露出了一个角,这个三角形是( )三角形。
A.锐角 B.直角
C.钝角 D.无法确定
D
(2)如图,下面是用木条钉成的四种支架,最不容易变形的是( )。
C
A
B
C
D
三角形具有稳定性,在生活中应用广泛,如斜拉桥、篮球架等都用到了三角形的稳定性。
(3)将一个正方形剪去一个角,剩下图形的内角和不可能是( )。
A.180° B.360°
C.540° D.720°
D
五边形的内角和是540°
四边形的内角和是360°
三角形的内角和是180°
6 整理和复习
2.图形与几何
数学人教版六年级下册
第2课时 平面图形的认识与测量(2)
问题导入
我们学过哪些平面图形的周长和面积计算公式呢?
教材第86页
这些计算公式是怎样推导出来的?它们之间有什么联系?
a
b
归纳整理
平面图形的面积计算公式
用数方格的方法推导。
把正方形看作长和宽相等的长方形。
a
a
通过割补、平移转化为长方形。
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
把两个完全一样的三角形通过旋转、平移拼成与它们等底等高的平行四边形。三角形的面积等于拼成的平行四边形面积的一半。
平面图形的面积计算公式
三角形的面积=底×高÷2
把两个完全一样的梯形通过旋转、平移拼成一个平行四边形。拼成的平行四边形的底等于梯形的上底与下底的和,高等于梯形的高,所以梯形的面积等于这个平行四边形面积的一半。
平面图形的面积计算公式
梯形的面积=(上底+下底)×高÷2
把一个圆分成若干份,剪拼成一个近似的长方形,这个长方形的长相当于圆周长的一半,宽相当于圆的半径。
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
πr
r
平面图形的面积计算公式
圆的面积=圆周率×半径的平方
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
三角形的面积=底×高÷2
梯形的面积=(上底+下底)×高÷2
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
平面图形的周长计算公式
圆的周长=圆周率×直径
长方形的周长=(长+宽)×2
正方形的周长=边长×4
平行四边形的周长=相邻两边的长度和×2
三角形的周长=三条边的长度和
梯形的周长=四条边的长度和
C=2(a+b)
C=4a
C=2(a+b)
C=a+b+c
C=a+b+c+d
C=πd=2πr
课堂练习
1.计算下面各图形的周长和面积。(单位:m)
教材第86页“做一做”第4题
周长:
30
40
50
30+40+50=120(m)
面积:
30×40÷2
=1200÷2
=600(m2)
周长:
6×2+10.5+7.5=30(m)
面积:
(6+10.5)×6÷2
=16.5×6÷2
=49.5(m2)
6
7.5
10.5
6
a
b
h
1.计算下面各图形的周长和面积。(单位:m)
3.14×6÷2
1.计算下面各图形的周长和面积。(单位:m)
周长:
=9.42+ 6 +10
=25.42(m)
面积:
=14.13+15
=29.13(m2)
5
3
6
+6
+5×2
3.14×(6÷2)2÷2
+5×3
(1)如下图(单位:cm),一个长方形框架变形后成了一个平行四边形,原来这个长方形的周长是( )cm,变形后的平行四边形面积是( )cm2。
2.填一填。
26
长方形的周长:
8×4=32(cm2)
(8+5)×2=26(cm)
原来长方形的宽为5 cm。
32
8
4
5
5
平行四边形的面积:
(2)如下图的平行四边形中,阴影部分的面积是6cm2,平行四边形的底是直角三角形的3倍,空白部分的面积是( )cm2。
6×2÷4=3(cm)
4 cm
3 cm
三角形的底=面积×2÷高。
3×3=9(cm)
9 cm
9×4-6=30(cm2)
三角形的底:
平行四边形的底:
空白部分的面积:
30
(3)如下图,张大爷用24米长的栅栏靠墙围成一块梯形菜地,这块菜地的面积是( )平方米。
54
6 m
24米长的栅栏分布在梯形的上底、高和下底三个部分,已知高是6米,则上、下底的和是(24-6)米。
(24-6)×6÷2=54(平方米)
(4)在一张长24 cm、宽20 cm的长方形纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2;如果改画最大的半圆,这个半圆的面积( )cm2。
62.8
314
圆的周长:3.14×20=62.8(cm)
圆的面积:3.14×(20÷2)2=314(cm2)
半圆的面积:3.14×(24÷2)2÷2=226.08(cm2)
226.08
圆的直径最大为20 cm。
半圆的直径最大为24 cm。
(5)如图,在大、小两个正方形中涂色部分的面积比是3∶2,则大、小两个正方形的边长比是( ),面积比是( )。
3∶2
9∶4
a
b
b
ab÷2 3
b2÷2 2
=-
-=-
a 3
b 2
涂色部分的面积比:
根据比的基本性质:
a2 32 9
b2 22 4
-=-=-
大、小正方形的面积比:
用a、b分别表示两个正方形的边长。
3.选一选。
(1)一个平行四边形相邻的两条边分别是6 cm、4 cm,量得一条边上的高是5 cm,这个平行四边形的面积是( )cm2。
A.30 B.24 C.20 D.10
C
4 cm
6 cm
小于4 cm
4 cm
4 cm
6 cm
小于6 cm
6 cm
以4 cm为底的高是5 cm
4×5=20(cm2)
(2)一个三角形的底和高相等,如果将底减少2分米,高增加2分米,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
B
原面积:6×6÷2=18(dm2)
新面积:(6-2)×(6+2)÷2=16(dm2)
16<18,面积减少了。
假设原三角形的底和高都是6分米。
(3)如下图,用三张同样大小的正方形纸分别剪掉图中涂色部分的图形,材料的利用率( )。
A.甲最高 B.乙最高 C.丙最高 D.相同
D
甲乙丙
甲:3.14×102÷4÷102=78.5%
乙:3.14×(10÷2)2÷102=78.5%
丙:3.14×(10÷2÷2)2×4÷102=78.5%
假设正方形的边长是10厘米。
(36+52)×42÷2÷1.5
=88×42÷2÷1.5
=1848÷1.5
=1232(棵)
答:这个果园最多可种1232棵果树。
4.一个梯形果园,上底是36米,下底是52米,高是42米。平均每棵果树占地1.5平方米,这个果园最多可种多少棵果树?
梯形的面积=(上底+下底)×高÷2
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
3.14×[(28÷2+2)2-(28÷2)2]
=3.14×[162-142]
=3.14×60
=188.4(平方米)
O
28 m
2 m
圆环的面积:S=π(R2-r2)
2×3.14×(28÷2+2)
=2×3.14×16
=100.48(米)
答:这条道路的面积是188.4平方米,外沿周长是100.48米。
O
外沿的周长:C=2πR
5.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
28 m
2 m
=3.14×27+3.14×2
=3.14×29
=91.06(平方米)
答:这只羊能吃到草的面积是91.06平方米。
6.草地上有一间房子,占地形状是边长4米的正方形。一只羊被拴在房子的外墙角处,已知栓羊的绳子长6米,这只羊能吃到草的面积是多少平方米?
2 m
6 m
3.14×62×-
3
4
+3.14×(6-4)2×-
1
2
如图,羊能吃到草的面积由三个扇形组成。
答:x的值是11.4。
7.已知下图中两块阴影部分的面积相等,求x的值。
扇形面积:3.14×102÷4=78.5(cm2)
10 cm
O
扇形面积减三角形面积
梯形面积减扇形面积
x cm
(10+x)×10÷2-78.5=78.5-50
三角形面积:10×10÷2=50(cm2)
(10+x)×10÷2=107
10+x=21.4
x=11.4
6 整理和复习
2.图形与几何
数学人教版六年级下册
第3课时 立体图形的认识与测量
情境导入
我们学过哪些立体图形?
它们各有什么特点?
归纳整理
长方体和正方体的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长
长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
教材第87页
圆柱和圆锥的特征
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面圆心之间的距离叫作高,有无数条长度相等的高。
顶点到底面圆心的距离叫作高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
立体图形的表面积计算公式
把长方体沿棱剪开,展开得到6个长方形,长方体的表面积就是这6个长方形的面积和。
长方体的表面积=(长×宽+长×高+宽×高)×2
a
b
h
a
b
h
前
后
左
右
上
下
立体图形的表面积计算公式
把正方体沿棱剪开,展开得到6个完全相同的正方形,正方体的表面积就是其中一个面面积的6倍。
正方体的表面积=棱长的平方×6
a
a
a
a
前
后
左
右
上
下
a
a
立体图形的表面积计算公式
把圆柱沿高和底面圆周剪开,侧面是一个长方形(正方形),圆柱的表面积就是三个面面积的和。
圆柱的表面积=底面积×2+底面周长×高
r
h
C
侧面
上底
下底
h
立体图形的表面积计算公式
圆柱的表面积=底面积×2+底面周长×高
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长的平方×6
圆柱的侧面积=底面周长×高
S=2(ab+ah+bh)
S=6a2
S侧=Ch=πdh=2πrh
S=S侧+2S底=2πrh+2πr2
立体图形的体积计算公式
用棱长为1 cm的小正方体摆成不同的长方体,长方体所含小正方体的数量就是长方体的体积。
长方体的体积=长×宽×高
a
b
h
正方体是长、宽、高都相等的特殊的长方体。
正方体的体积=棱长的立方
a
a
a
立体图形的体积计算公式
把圆柱沿底面直径切成若干等份,可以拼成一个近似的长方体,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高。
圆柱的体积=底面积×高
立体图形的体积计算公式
把圆锥形容器里的水倒入与它等底、等高的圆柱形容器内,3次才能倒满。
圆锥的体积=与圆锥等底、等高的圆柱的体积×-
13
长方体的体积=长×宽×高
正方体的体积=棱长的立方
圆柱的体积=圆周率×半径的平方×高
V=abh
V=a3
V=πr2h
立体图形的体积计算公式
圆锥体积=底面积×高×-
13
V=-S底h=-πr2h
13
13
长方体、正方体、圆柱的体积:V=S底h
课堂练习
1.判断对错,对的画“√”,错的画“×”。
绕着宽所在的直线为轴旋转一周也可以形成圆柱。
(1)长方形只有绕着长所在的直线为轴旋转一周才能形成圆柱。 ( )
(2)任意一个三角形绕它的一条边所在的直线为轴旋转都能形成圆锥。 ( )
(3)体积相等的两个长方体的底面积一定相等。( )
直角三角形绕着直角边所在的直线旋转才能形成圆锥。
×
×
体积是底面积和高的积,高不确定,底面积不一定相等。
×
2.怎样测量出一块拳头大的鹅卵石的体积?
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
求不规则物体体积的方法:
教材第87页“做一做”第1题
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
上升的水的体积就是鹅卵石的体积。
用“底面积×上升的高度”来计算。
2.怎样测量出一块拳头大的鹅卵石的体积?
前面
3.在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
左面
上面
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
教材第87页“做一做”第2题
4.小明用一根铁丝做成一个正方体框架。已知这个正方体框架的一个面的面积是49平方厘米,这根铁丝至少长( )厘米。
84
正方体的每个面都是正方形,因为49=72,所以正方体的棱长为7厘米,铁丝的长度也就是12条棱的长度和,即12×7=84(厘米)。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
22
这个物体的表面由22个正方形围成,每个正方形的面积是1×1=1(平方厘米),所以表面积是20×1=1(平方厘米)。
求表面积可以数一数表面有几个正方形。
5.如图是由一些棱长为1厘米的小正方体摆成的,它的表面积是( )平方厘米;至少添加( )个这样的小正方体能成为一个大长方体。
7
拼成的大长方体的长至少是3厘米,宽至少是2厘米,高至少是2厘米,因此一共需要3×2×2=12(个)小正方体,已有5个,至少添加12-5=7(个)。
22
先思考拼成的大长方体一共需要多少个小正方体。
6.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
7.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
8.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
12÷3=4(cm)
9.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,如果把它捏成同样高的一个圆柱,那么该圆柱的底面积是多少平方厘米?
圆锥体积=底面积×高×-
13
12×6×-=24(立方厘米)
13
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
圆锥变成圆柱的过程中,体积不变。
答:该圆柱的底面积是4平方厘米。
Thank you!
