7.1.1数系的扩充和复数的概念 课件(共29张PPT)
文档属性
| 名称 | 7.1.1数系的扩充和复数的概念 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 42.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
菏泽外国语学校 聂张坤
7.1.1 数系的扩充和复数的概念
第七章 复数
数学来源于生活,高于生活。
思考?
学习目标:
1、了解引进虚数单位的必要性,了解数系的扩充过程
2、理解在数系扩充中由实数集到复数集出现的基本概念
3、掌握复数的表示方法、分类及复数相等的充要条件
学习目标
对于一元二次方程 ,当 时,没有实数根。因此,在研究代数方程的过程中,如果限于实数集,有些问题就无法解决。
事实上,早在古希腊时代,数学家在研究解方程问题时就遇到了负实数开平方的问题,但他们一直在回避。直到1545年,意大利数学家卡丹在用求根公式,因式分解两种方法同时求解一些特殊的一元三次方程时,得到了无法理解的结果......
一、创设情境,引入新知
解方程:
方法1:
用三次方程求根公式(卡丹公式)
解得:
方法2:
用因式分解
解得:
得到:
16世纪
数学家的困惑
一、创设情境,引入新知
问题1从方程的角度看,负实数能不能开平方,实际上就是方程 (a>0)有没有解的问题。能不能把这类问题再进一步简化,最终转化为最简单的方程x2+1=0有没有解的问题呢?
追问x2+1=0在实数集中无解,能否引入新数,适当地扩充实数集,使这个方程在新数集中有解呢?
二、创设情境,合作探究
远古的人类,为了统计捕获的野兽和采集的野果,历经漫长的岁月,创造了自然数,自然数集记为N。自然数是现实世界最基本的数量,是全部数学的发源地。自然数的加法与乘法满足交换律、结合律及分配律。
随后为了表示具有相反意义的量,负数的概念就出现了,我国是认识正负数最早的国家,《九章算术》中就有了正负数的记载。负数概念引进后,就把数集扩充到整数集Z,运算法则同样适用。
随着历史的发展,为了公平分配物质印度人引进了分数,但分数的确切定义,科学表示及分数算法,都是中国最早提出的。分数运算也满足加法与乘法的运算律。分数概念引进后,就把数集扩充到有理数集Q,运算法则同样适用。
公元前几百年,希腊人发现边长为1的正方形和正五边形对角线的长都不是分数,从此人们知道了世间还存在另一类数无理数。有理数集与无理数集合并在一起就构成实数集R。
数系的每一次扩充,都是基于两个方面的原因:社会生产实践的需要和数学自身发展的需要。
阅读
自然数集
整数集
有理数集
实数集
刻画相反意义的量
引入了
负数
解决测量等分问题
引入了
分数
解决度量正方体对角线等问题
引入了
无理数
计数的需要
引入了
自然数
从社会生产实践的需要来看
自然数
负整数
整数
无理数
有理数
分数
实数
随着社会发展,数系在不断扩充.
二、创设情境,合作探究
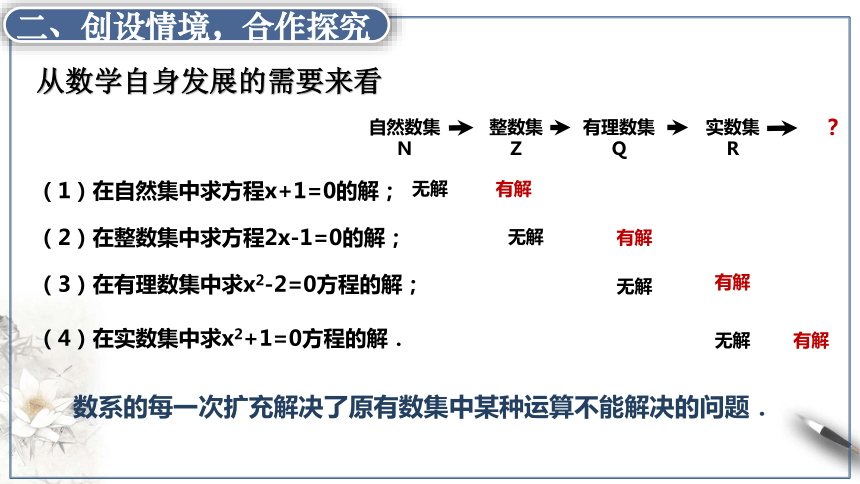
从数学自身发展的需要来看
(2)在整数集中求方程2x-1=0的解;
自然数集
N
整数集
Z
有理数集
Q
实数集
R
无解
有解
无解
有解
有解
无解
(3)在有理数集中求x2-2=0方程的解;
数系的每一次扩充解决了原有数集中某种运算不能解决的问题.
(4)在实数集中求x2+1=0方程的解.
无解
有解
?
(1)在自然集中求方程x+1=0的解;
二、创设情境,合作探究
数系扩充后,在运算上遵循了什么规则?
如果没有运算,数只是孤立的符号!
有理数集
实数集
引入了无理数
运算
运算律
+ (—)
×( ÷)
+ (—)
×( ÷)
交换律
结合律
分配律
交换律
结合律
分配律
数系扩充规则:
数集扩充后,在新数集中规定的加法运算和乘法运算,与原来数集中规定的加法和乘法运算协调一致,并且加法和乘法都满足交换律和结合律,乘法对加法满足分配律.
二、创设情境,合作探究
问题2类比从自然数集到实数集的扩充过程,特别是从有理数集到实数集的扩充过程,你能设想一种方法,使方程x2+1=0有解吗?
我们可以引入一个数“i”,使i2=-1,
这样x=i就是方程x2+1=0的解.
历史上,新数i是瑞士著名数学家欧拉在1777年首次提出的,他用了“imaginary”一词的首字母,本意是这个数是虚幻的.
三、依据规则,引入概念
问题3根据上述规则,你能说出实数集经过扩充后,得到的新数集由哪些数组成吗?你能写出新数的一般形式吗?
加法运算
乘法运算
实数
新数
3+i
a+i
2i
bi
3+2i
a+bi(a,b∈R)
依据规则:
在新数集中规定的加法运算和乘法运算,与原来数集中规定的加法和乘法运算协调一致。
三、依据规则,引入概念
(1)形如 的数叫做复数,通常用字母 z 表示.
(2)全体复数所形成的集合叫做复数集,一般用C 表示.
实部
虚部
i 叫虚数单位
三、依据规则,引入概念
1545年意大利有名的数学家卡丹第一次开始讨论负数开平方的问题,当时复数被他称作“诡辩量”。
几乎过了100年,笛卡尔才给这种“虚幻之数”取了一个名字——虚数。但是又过了140年,欧拉还是说这种数只是存在于“幻想”,并用i(imaginary,即虚幻的缩写)来表示它的单位。
1832年德国高斯给出了复数的定义,并把复数与直角坐标平面内的点一一对应起来.
1837年,英国数学家哈密顿用有序实数对(a,b)定义了复数及其运算,并说明复数的加、乘运算满足实数的运算律。
这样历经300年的努力,数系从实数系向复数系的扩充才得以大功告成.
阅读
阅读:复数系是怎么建立的?
阅读
这是一个漫长而曲折的过程,其中充满着数学家的丰富,深邃的想象力和创造力,表现了数学家不屈不挠,精益求精的精神。我们看到,人们是在解决纯粹数学问题的过程中发现复数的,但它现在在流体力学,信号分析等学科中得到了广泛的应用。1843年,英国数学家哈密顿在复数基础上构造了四元数,从而导致了物理学中著名的麦克斯韦方程的建立,显示了人类理性思维的强大作用!
高斯
卡丹
笛卡尔
欧拉
哈密顿
例1、指出下列复数的实部和虚部:
(1)4 (2)2-3i (3)5i+ (4)-6i
(5)0 (6) (7)2+ (8)π
虚部b=0
虚部b≠0
实部a=0
三、依据规则,引入概念
练习:把下列式子化为a+bi(a,b∈R)的形式,并分别指出它们的实部和虚部。
2-i= -2i= 5= 0=
三、依据规则,引入概念
问题4我们已经将实数集扩充到复数集,那么复数集C和实数集R之间有什么关系?你能对复数a+bi(a,b∈R)进行分类,并用韦恩图表示它们之间的关系吗?
四、根据特点,实际应用
虚部b=0
虚部b≠0
实部a=0
实数
虚数
纯虚数
复数a+bi
复数的分类
四、根据特点,实际应用
复数集C
实数R
纯虚数
虚数
四、根据特点,实际应用
例2、实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
解: (1) 当 ,即 时,复数z 是实数.
(2)当 ,即 时,复数z 是虚数.
(3)当
即 时,复数z是
纯虚数.
四、根据特点,实际应用
练习:当m为何实数时,复数
(1)实数 (2)虚数 (3)纯虚数
m2-1=0 ∴m=±1
m2-1≠0
∴m≠±1
m2+m-2=0且
m2-1≠0
∴m=-2
四、根据特点,实际应用
问题5 我们知道复数集是由形如a+bi(a,b∈R)的数组成的,为了保证集合中元素的互异性(确定性),我们需要明确集合中两个元素相等的含义,请阅读教科书,说说两个复数相等的含义.
四、根据特点,实际应用
两个复数相等的充要条件
特别地
当且仅当
每个复数都可以由实部和虚部这两个实数唯一确定.
四、根据特点,实际应用
四、根据特点,实际应用
问题6 3+2i与2能比较大小吗?两个复数可以比较大小吗?
1.两个不全是实数的复数不能比大小,只能由定义判断它们是否相等;
2.若两个复数能比较大小,则这两个复数一定全是实数
若 ,
则
四、根据特点,实际应用
1、以3i- 的虚部为实部,以3i2+ i的实部为虚部的复数是()A 3-3i B 3+i C - + i D + i
2、a=0是复数a+bi(a,b∈R)为纯虚数的()
A 必要条件 B 充分条件 C 充要条件 D 非必要非充分条件
3、若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为 。
四、根据特点,实际应用
1. 虚数单位i的引入,数系的扩充;
2. 复数有关概念:
复数的代数形式:
复数的实部、虚部、虚数单位
复数相等
复数的分类
五、课堂总结,反思提炼
五、课堂总结,反思提炼
1、数系还能再扩充吗?
2、作为一个新数集,如何定义复数的四则运算?
菏泽外国语学校 聂张坤
菏泽外国语学校 聂张坤
7.1.1 数系的扩充和复数的概念
第七章 复数
数学来源于生活,高于生活。
思考?
学习目标:
1、了解引进虚数单位的必要性,了解数系的扩充过程
2、理解在数系扩充中由实数集到复数集出现的基本概念
3、掌握复数的表示方法、分类及复数相等的充要条件
学习目标
对于一元二次方程 ,当 时,没有实数根。因此,在研究代数方程的过程中,如果限于实数集,有些问题就无法解决。
事实上,早在古希腊时代,数学家在研究解方程问题时就遇到了负实数开平方的问题,但他们一直在回避。直到1545年,意大利数学家卡丹在用求根公式,因式分解两种方法同时求解一些特殊的一元三次方程时,得到了无法理解的结果......
一、创设情境,引入新知
解方程:
方法1:
用三次方程求根公式(卡丹公式)
解得:
方法2:
用因式分解
解得:
得到:
16世纪
数学家的困惑
一、创设情境,引入新知
问题1从方程的角度看,负实数能不能开平方,实际上就是方程 (a>0)有没有解的问题。能不能把这类问题再进一步简化,最终转化为最简单的方程x2+1=0有没有解的问题呢?
追问x2+1=0在实数集中无解,能否引入新数,适当地扩充实数集,使这个方程在新数集中有解呢?
二、创设情境,合作探究
远古的人类,为了统计捕获的野兽和采集的野果,历经漫长的岁月,创造了自然数,自然数集记为N。自然数是现实世界最基本的数量,是全部数学的发源地。自然数的加法与乘法满足交换律、结合律及分配律。
随后为了表示具有相反意义的量,负数的概念就出现了,我国是认识正负数最早的国家,《九章算术》中就有了正负数的记载。负数概念引进后,就把数集扩充到整数集Z,运算法则同样适用。
随着历史的发展,为了公平分配物质印度人引进了分数,但分数的确切定义,科学表示及分数算法,都是中国最早提出的。分数运算也满足加法与乘法的运算律。分数概念引进后,就把数集扩充到有理数集Q,运算法则同样适用。
公元前几百年,希腊人发现边长为1的正方形和正五边形对角线的长都不是分数,从此人们知道了世间还存在另一类数无理数。有理数集与无理数集合并在一起就构成实数集R。
数系的每一次扩充,都是基于两个方面的原因:社会生产实践的需要和数学自身发展的需要。
阅读
自然数集
整数集
有理数集
实数集
刻画相反意义的量
引入了
负数
解决测量等分问题
引入了
分数
解决度量正方体对角线等问题
引入了
无理数
计数的需要
引入了
自然数
从社会生产实践的需要来看
自然数
负整数
整数
无理数
有理数
分数
实数
随着社会发展,数系在不断扩充.
二、创设情境,合作探究
从数学自身发展的需要来看
(2)在整数集中求方程2x-1=0的解;
自然数集
N
整数集
Z
有理数集
Q
实数集
R
无解
有解
无解
有解
有解
无解
(3)在有理数集中求x2-2=0方程的解;
数系的每一次扩充解决了原有数集中某种运算不能解决的问题.
(4)在实数集中求x2+1=0方程的解.
无解
有解
?
(1)在自然集中求方程x+1=0的解;
二、创设情境,合作探究
数系扩充后,在运算上遵循了什么规则?
如果没有运算,数只是孤立的符号!
有理数集
实数集
引入了无理数
运算
运算律
+ (—)
×( ÷)
+ (—)
×( ÷)
交换律
结合律
分配律
交换律
结合律
分配律
数系扩充规则:
数集扩充后,在新数集中规定的加法运算和乘法运算,与原来数集中规定的加法和乘法运算协调一致,并且加法和乘法都满足交换律和结合律,乘法对加法满足分配律.
二、创设情境,合作探究
问题2类比从自然数集到实数集的扩充过程,特别是从有理数集到实数集的扩充过程,你能设想一种方法,使方程x2+1=0有解吗?
我们可以引入一个数“i”,使i2=-1,
这样x=i就是方程x2+1=0的解.
历史上,新数i是瑞士著名数学家欧拉在1777年首次提出的,他用了“imaginary”一词的首字母,本意是这个数是虚幻的.
三、依据规则,引入概念
问题3根据上述规则,你能说出实数集经过扩充后,得到的新数集由哪些数组成吗?你能写出新数的一般形式吗?
加法运算
乘法运算
实数
新数
3+i
a+i
2i
bi
3+2i
a+bi(a,b∈R)
依据规则:
在新数集中规定的加法运算和乘法运算,与原来数集中规定的加法和乘法运算协调一致。
三、依据规则,引入概念
(1)形如 的数叫做复数,通常用字母 z 表示.
(2)全体复数所形成的集合叫做复数集,一般用C 表示.
实部
虚部
i 叫虚数单位
三、依据规则,引入概念
1545年意大利有名的数学家卡丹第一次开始讨论负数开平方的问题,当时复数被他称作“诡辩量”。
几乎过了100年,笛卡尔才给这种“虚幻之数”取了一个名字——虚数。但是又过了140年,欧拉还是说这种数只是存在于“幻想”,并用i(imaginary,即虚幻的缩写)来表示它的单位。
1832年德国高斯给出了复数的定义,并把复数与直角坐标平面内的点一一对应起来.
1837年,英国数学家哈密顿用有序实数对(a,b)定义了复数及其运算,并说明复数的加、乘运算满足实数的运算律。
这样历经300年的努力,数系从实数系向复数系的扩充才得以大功告成.
阅读
阅读:复数系是怎么建立的?
阅读
这是一个漫长而曲折的过程,其中充满着数学家的丰富,深邃的想象力和创造力,表现了数学家不屈不挠,精益求精的精神。我们看到,人们是在解决纯粹数学问题的过程中发现复数的,但它现在在流体力学,信号分析等学科中得到了广泛的应用。1843年,英国数学家哈密顿在复数基础上构造了四元数,从而导致了物理学中著名的麦克斯韦方程的建立,显示了人类理性思维的强大作用!
高斯
卡丹
笛卡尔
欧拉
哈密顿
例1、指出下列复数的实部和虚部:
(1)4 (2)2-3i (3)5i+ (4)-6i
(5)0 (6) (7)2+ (8)π
虚部b=0
虚部b≠0
实部a=0
三、依据规则,引入概念
练习:把下列式子化为a+bi(a,b∈R)的形式,并分别指出它们的实部和虚部。
2-i= -2i= 5= 0=
三、依据规则,引入概念
问题4我们已经将实数集扩充到复数集,那么复数集C和实数集R之间有什么关系?你能对复数a+bi(a,b∈R)进行分类,并用韦恩图表示它们之间的关系吗?
四、根据特点,实际应用
虚部b=0
虚部b≠0
实部a=0
实数
虚数
纯虚数
复数a+bi
复数的分类
四、根据特点,实际应用
复数集C
实数R
纯虚数
虚数
四、根据特点,实际应用
例2、实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
解: (1) 当 ,即 时,复数z 是实数.
(2)当 ,即 时,复数z 是虚数.
(3)当
即 时,复数z是
纯虚数.
四、根据特点,实际应用
练习:当m为何实数时,复数
(1)实数 (2)虚数 (3)纯虚数
m2-1=0 ∴m=±1
m2-1≠0
∴m≠±1
m2+m-2=0且
m2-1≠0
∴m=-2
四、根据特点,实际应用
问题5 我们知道复数集是由形如a+bi(a,b∈R)的数组成的,为了保证集合中元素的互异性(确定性),我们需要明确集合中两个元素相等的含义,请阅读教科书,说说两个复数相等的含义.
四、根据特点,实际应用
两个复数相等的充要条件
特别地
当且仅当
每个复数都可以由实部和虚部这两个实数唯一确定.
四、根据特点,实际应用
四、根据特点,实际应用
问题6 3+2i与2能比较大小吗?两个复数可以比较大小吗?
1.两个不全是实数的复数不能比大小,只能由定义判断它们是否相等;
2.若两个复数能比较大小,则这两个复数一定全是实数
若 ,
则
四、根据特点,实际应用
1、以3i- 的虚部为实部,以3i2+ i的实部为虚部的复数是()A 3-3i B 3+i C - + i D + i
2、a=0是复数a+bi(a,b∈R)为纯虚数的()
A 必要条件 B 充分条件 C 充要条件 D 非必要非充分条件
3、若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为 。
四、根据特点,实际应用
1. 虚数单位i的引入,数系的扩充;
2. 复数有关概念:
复数的代数形式:
复数的实部、虚部、虚数单位
复数相等
复数的分类
五、课堂总结,反思提炼
五、课堂总结,反思提炼
1、数系还能再扩充吗?
2、作为一个新数集,如何定义复数的四则运算?
菏泽外国语学校 聂张坤
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
