沪教版八年级数学下册试题 第20章《一次函数》综合复习题(含解析)
文档属性
| 名称 | 沪教版八年级数学下册试题 第20章《一次函数》综合复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览




文档简介
第20章《一次函数》综合复习题
一、单选题
1.如图,点、以及直线在的正方形网格中,每个小正方形的边长为单位1.在网格中建立直角坐标系后,、两点的坐标分别、,在直线上找一点使得最小,则点的坐标为( )
A. B. C. D.
2.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段OA、PB分别反映了小张、小王步行所走的路程S(千米)与时间t(分钟)的函数关系,根据图像提供的信息,小王比小张早到乙地的时间是( )分钟.
A.4 B.6 C.16 D.10
3.如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,点在线段上,轴于点,则周长的最小值为( ).
A. B. C.4 D.
4.如图所示,直线y=x+4与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,则周长的最小值是( )
A. B. C. D.
5.对于实数,定义符号其意义为:当时,;当时,.例如:,若关于的函数,则该函数的最大值是( )
A. B. C. D.
二、填空题
6.如图,在平面直角坐标系中,点A,,,…,都在直线上,点,,…都在直线上,在轴上,且……,以为直角边在两条直线内部作等腰直角三角形,在边上;再以为直角边在两条直线内部作等腰直角三角形,在边上;…如此做下去,则的面积用含有的代数式表示为__________.
7.如图,在直角坐标xoy系中,点A的坐标是(2,0)、点B的坐标是(0,2)、点C的坐标是(0,3),若直线CD的解析式为y=-x+3,则S△ABD为___________.
8.如图,在平面直角坐标系中,直线与轴交于点,与轴交点于,且,°,以为边长作等边三角形,过点作平行于轴,交直线于点,以为边长作等边三角行,过点作平行于轴,交直线于点,以为边长坐等三角形,…,则点的横坐标是___________.
9.在平面直角坐标系中,直线分别交x轴、y轴于C、A两点.将射线绕着点A顺时针旋转,得到射线.点D为上的动点,点B为上的动点,点C在的内部.
(1)周长的最小值是____________________;
(2)当的周长取得最小值,且时,的面积为__________.
10.如图,反比例函数的图象与直线()交于,两点(点在点左侧),过点作轴的垂线,垂足为点,连接,,图中阴影部分的面积为6,则的值为______.
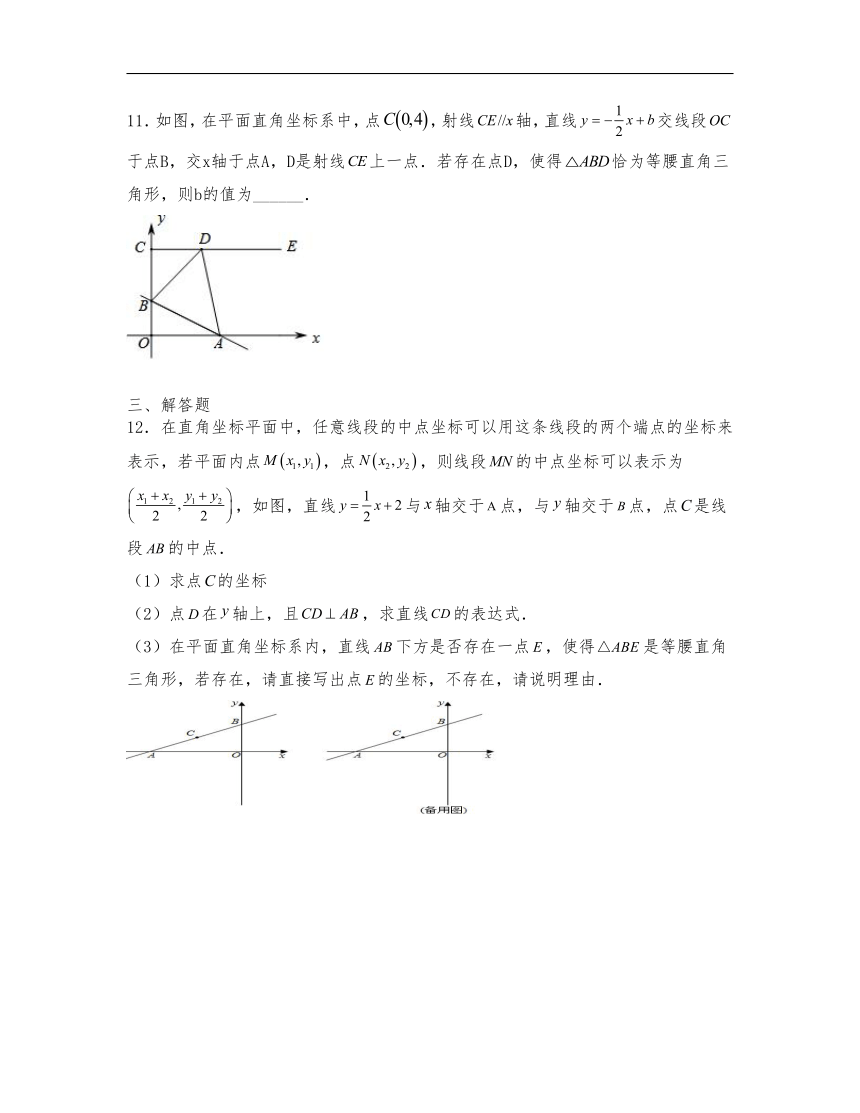
11.如图,在平面直角坐标系中,点,射线轴,直线交线段于点B,交x轴于点A,D是射线上一点.若存在点D,使得恰为等腰直角三角形,则b的值为______.
三、解答题
12.在直角坐标平面中,任意线段的中点坐标可以用这条线段的两个端点的坐标来表示,若平面内点,点,则线段的中点坐标可以表示为,如图,直线与轴交于点,与轴交于点,点是线段的中点.
(1)求点的坐标
(2)点在轴上,且,求直线的表达式.
(3)在平面直角坐标系内,直线下方是否存在一点,使得是等腰直角三角形,若存在,请直接写出点的坐标,不存在,请说明理由.
13.已知,如图,在平面直角坐标系中,一次函数与轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,将△ABC绕着顶点B旋转后,点C的对应点C’落在y轴上,点A的对应点A’恰好落在反比例函数 的图像上.
(1)求的面积;
(2)如果的值为6 (即反比例函数为),求点的坐标;
(3)如果四边形是梯形,求的值.
14.如图,在直角坐标平面内,点是坐标原点,点坐标为,将直线绕点顺时针旋转后得到直线.
(1)求直线的表达式;
(2)求的值;
(3)在直线上有一点,其纵坐标为1.若轴上存在点,使是等腰三角形,请直接写出满足要求的点的坐标.
15.已知:如图,在中,,,,AD平分,交BC边于点D.点E是边AB上一动点(与点A、B不重合).过点E作,垂足为点G,与射线AC交于点F.
(1)当点F在边AC上时,
①求证:;
②设,,求y与x之间的函数解析式并写出定义域.
(2)当是等腰三角形时,求BE的长.
16.如图,正方形ABCD的顶点A、B落在x轴正半轴上,点C落在正比例函数y=kx(k>0)上,点D落在直线y=2x上,且点D的横坐标为a.
(1)直接写出A、B、C、D各点的坐标(用含a的代数式表示);
(2)求出k的值;
(3)将直线OC绕点O旋转,旋转后的直线将正方形ABCD的面积分成1:3两个部分,求旋转后得到的新直线解析式.
17.已知:如图,在直角坐标平面中,点在轴的负半轴上,直线经过点,与轴相交于点,点是点关于原点的对称点,过点的直线轴,交直线于点,如果.
(1)求直线的表达式;
(2)如果点在直线上,且是等腰三角形,请求出点的坐标.
18.浦东新区在创建文明城区的活动中,有两段长度相等的彩色道砖路面的铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设的彩色道砖路面的长度(米)与施工时间(时)之间关系的部分图像.请根据题意回答下列问题:
(1)甲队每小时施工_________米;
(2)乙队在时段内,与之间的函数关系式是_________;
(3)在时段内,甲队比乙队每小时快_________米;
(4)如果甲队施工速度不变,乙队在小时后,施工速度增加到米/时,结果两队同时完成了任务.则甲队从开始施工到完工所铺设的彩色道砖路面的长度为_________米.
19.如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
20.观摩、学习是我们生活的一部分,而在观摩中与展览品保持一定的距离是一种文明的表现.某学校数学业余学习小组在平面直角坐标系xOy有关研讨中,将到线段PQ所在的直线距离为的直线,称为直线PQ的“观察线”,并称观察线上到P、Q两点距离和最小的点L为线段PQ的“最佳观察点”.
(1)如果P(1,),Q(4,),那么在点A(1,0),B(,2),C(,3)中,处在直线PQ的“观察线”上的是点 ;
(2)求直线y=x的“观察线”的表达式;
(3)若M(0,﹣1),N在第二象限,且MN=6,当MN的一个“最佳观察点”在y轴正半轴上时,直接写出点N的坐标;并按逆时针方向联结M、N及其所有“最佳观察点”,直接写出联结所围成的多边形的周长和面积.
21.已知一次函数的图像与轴、轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
(1)求点的坐标;
(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得,求点M的坐标;
(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
22.如图,已知直线y=﹣x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.
23.如题,,点是边的中点,点是边上的一个动点,作交于点,的延长线交线段于点.
(1)如图①,当点于点重合时,求证:;
(2)设,梯形的面积为,求与的函数解析式,并写出定义域.
24.某地A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元、25元,从B村运往C、D两处的费用分别为每吨15元、18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元、yB元.
(1)请填写下表,并求出yA、yB与x之间的函数表达式;
(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
25.如图,在平面直角坐标系中,直线经过点且与直线: 平行,直线与轴、轴分别交于点B、C.
(1)求直线l1的表达式及其与轴的交点D的坐标;
(2)判断四边形ABCD是什么四边形?并证明你的结论;
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.
26.如图,已知一次函数的图像与x轴、轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
27.某校八年级举行“生活中的数学”数学小论文比赛活动,购买A、B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元,根据比赛设奖情况,需要购买两种笔记本共30本,若学校决定购买本次笔记本所需资金不能超过280元,设买A种笔记本x本.
(1)根据题意完成以下表格(用含x的代数式表示)
(2)那么最多能购买A笔记本多少本?
(3)若购买B笔记本的数量要小于A笔记本的数量的3倍,则购买这两种笔记本各多少本时,费用最少,最少的费用是多少元?
28.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
29.如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
30.已知一次函数y=-x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
答案
一、单选题
1.B
【分析】根据题意建立直角坐标系,作B关于l的对称点C,连接AC,则AC与l的交点即为所求点P,接着写出直线AC与直线l的函数解析式,联立得到关于P点坐标x、y的二元一次方程组,解方程组即可得到P点坐标.
【详解】解:如图,由题意可建立直角坐标系,作B关于l的对称点C,连接AC,则AC与l的交点即为所求点P,
由图可写出l的函数解析式为y=-1,
设直线AC的函数为y=kx+b,则把A、C坐标代入可得:,
解之可得:k=-1,b=1,
∴直线AC的函数为y=-x+1,
∴有,解之得:x=2,y=-1,
∴P点坐标为(2,-1),
故选B .
2.B
【分析】由函数图象求出、解析式,再把代入解析式就可以求出小张、小王所用时间.
【详解】解:由图象可知:
设的解析式为:,
经过点,
,
得,
函数解析式为:①,
把代入①得:,
解得:,
小张到达乙地所用时间为96(分钟);
设的解析式为:,
,
解得:,
的解析式为:②,
把代入②得:,
解得:,
则小王到达乙地的时间为小张出发后90(分钟),
小王比小张早到(分钟),
故选:B.
3.B
【分析】先根据一次函数的解析式可得,设点P的坐标为,从而可得,再根据三角形的周长公式可得周长为,然后根据垂线段最短可得当时,OP取得最小值,最后利用等腰直角三角形的判定与性质求出OP的最小值即可得.
【详解】对于一次函数,
当时,,解得,即,,
当时,,即,,
由题意,设点P的坐标为,
则,
因此,周长为,
要使周长最小,则只需OP取得最小值,
由垂线段最短可知,当时,OP取得最小值,
又,
是等腰直角三角形,,
此时,
周长的最小值为,
故选:B.
4.D
【分析】如图(见解析),先根据轴对称的性质可得,再根据三角形的周长公式、两点之间线段最短可得周长的最小值为FG的长,然后根据直线AB的解析式求出点B的坐标,从而可得点C、G的坐标,最后根据等腰直角三角形的判定与性质可得点F的坐标,据此利用两点之间的距离公式即可得出答案.
【详解】如图,作点C关于AB的对称点F,关于AO的对称点G,连接DF、EG、BF,
由轴对称的性质得:,
周长为,
由两点之间线段最短得:当点在同一直线上时,取得最小值,最小值为FG的长,
对于一次函数,
当时,,解得,即,
当时,,即,
,
点C为OB的中点,
,
点G为点C关于AO的对称点,
,
又,
,
,
,
,
是等腰直角三角形,,即轴,
,
则,
即周长的最小值是,
故选:D.
5.C
二、填空题
6.
【分析】根据点A,,,…,都在直线上先求出,再根据点,,…都在直线上,求出,由在轴上,且……,以为直角边在两条直线内部作等腰直角三角形,得到的横坐标为2,同理依次类推,得出 ,,,最后算出面积即可.
【详解】解:当x=0时,,,
∴,
∵,
∴的横坐标为2,
∴,
∴,
∵,
∴的横坐标为,
∴,
∴,
∵,
∴的横坐标为,
∴,
∴,
∴,,,
∴ ,,,
∴=,
=
=,
故答案为:.
7.1
【解析】分析:先求出直线AB的解析式,根据直线AB与直线CD的k值相等可得出它们平行,根据平行线间的距离处处相等可得出,即可得出答案.
详解:设直线AB的解析式为,
∵A的坐标是(2,0)、点B的坐标是(0,2)、
∴,
解得,
∴直线AB的解析式为,
∵直线CD的解析式为y=-x+3,
∴AB//CD,
∴,
∵点A的坐标是(2,0)、点B的坐标是(0,2)、点C的坐标是(0,3),
∵BC=1,AO=2,
∴,
∴
故答案为:1.
8.
【分析】过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为,,A2的横坐标为, A3的横坐标为,进而得到An的横坐标为,据此可得点A10的横坐标.
【详解】解:如图所示,过A1作A1A⊥OB1于A,则OA=OB1=,
即A1的横坐标为=,
∵°,
∴∠OB1D=30°,
∵A1B2//x轴,
∴∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=A1B2=1,
即A2的横坐标为+1=,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=A2B3=2,
即A3的横坐标为+1+2=,
同理可得,A4的横坐标为+1+2+4=,
由此可得,An的横坐标为,
∴点A10的横坐标是,
故答案为.
9.
【分析】(1)可作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.连接C1C2.利用两点之间线段最短,可得到当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
(2)根据(1)的作图可知四边形AC1CC2的对角互补,结合轴对称可得∠BCD=90°.利用勾股定理得到CB2+CD2=BD2=()2,因为CB+CD=4﹣,可推出CB CD的值,进而求出三角形的面积.
【详解】(1)∵直线y=与x轴、y轴分别交于C、A两点,把y=0代入,解得x=2,把x=0代入,解得y=2,
∴点C的坐标为(2,0),点A的坐标为(0,2).
∴AC=4.
作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.由轴对称的性质,可知CD=C1D,CB=C2B.
∴CB+BD+CD=C2B+BD+C1D=C1C2连接AC1、AC2,
可得∠C1AD=∠CAD,∠C2AB=∠CAB,AC1=AC2=AC=4.
∵∠DAB=45°,
∴∠C1AC2=90°.
连接C1C2.,
∵两点之间线段最短,
∴当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
∴△BCD的周长的最小值为4.
故答案为:4.
(2)根据(1)的作图可知四边形AECF的对角互补,其中∠DAB=45°,因此,∠C2CC1=135°.
即∠BCC2+∠DCC1+∠BCD=135°,
∴2∠BCC2+2∠DCC1+2∠BCD=270°①,
∵∠BC2C=∠BCC2,∠DCC1=∠DC1C,∠BC2C+∠DC1C+∠BCC2+∠DCC1+∠BCD=180°,
∴2∠BCC2+2∠DCC1+∠BCD=180°②,
①-②得,∠BCD=90°.
∴CB2+CD2=BD2=()2=,
∵CB+CD=4﹣,
(CB+CD)2=CB2+CD2+2CB CD,
∴2CB CD=(CB+CD)2-(CB2+CD2)=
∴.
故答案为:
10.
【分析】首先由已知得到S△BFG=2S△OEC,从而可得A、B横坐标的关系,再设A、B坐标代入y= x+m,即可求解.
【详解】解:过点A、B分别作y轴和x轴的垂线,垂足分别为R、F,
设点M是AB的中点,
由,整理得:x2 mx+6=0,
由题意可得x2 mx+6=0有两个不相等的实数根分别设为x1,x2,
则x1+x2=m,y1+y2= x1+m x2+m=m,
则点M的坐标为(m,m),
设直线AB交x轴于点G,交y轴于点H,
对于y= x+m,令x=0,则y=m,令y=0,则x=m,
∴点G、H的坐标分别为(m,0)、(0,m),
则点HG中点的坐标为(m,m),
即点M也为GH的中点,故AH=BG,
∵AR∥x轴,
∴∠HAR=∠BGF,
∵∠HRA=∠BFG=90°,
∴△HRA≌△BFG(AAS),
∴AR=OC=FG,
∴S△HRA=S△BFG,
∵S△AEO+S△OCE+S△OCE+S四边形ECFB=|k|+|k|=6,
而阴影部分的面积=S△AEO+S四边形EBFC+S△BFG=6,
∴S△BFG=2S△OEC,
即2××CO EC=×BF FG,
而OC=FG,
∴EC=BF,
即EC是△OBF的中位线,
故设点A的坐标为(t, ),则点B(2t,),
将点A、B的坐标代入一次函数表达式得:,解得(不合题意的值已舍去),
故答案为:.
11.或或2
【分析】分三种情况讨论:①当∠ABD=90°时,证得△DBC≌△BAO,得出BC=OA,即4-b=2b,求得b=;②当∠ADB=90°时,作AF⊥CE于F,同理证得△BDC≌△DAF,得出BC=DF,即2b-4=4-b,求得b=;③当∠DAB=90°时,作DF⊥OA于F,同理证得△AOB≌△DFA,得出OA=DF,即2b=4,解得b=2.
【详解】解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,
∴∠DBC=∠BAO,
由直线交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
∵点C(0,4),
∴OC=4,
∴BC=4-b,
在△DBC和△BAO中,
,
∴△DBC≌△BAO(AAS),
∴BC=OA,
即4-b=2b,
∴b=,
②当∠ADB=90°时,如图2,作AF⊥CE于F,
同理证得△BDC≌△DAF,
∴CD=AF=4,BC=DF,
∵OB=b,OA=2b,
∴BC=DF=2b-4,
∵BC=4-b,
∴2b-4=4-b,
∴b=;
③当∠DAB=90°时,如图3,作DF⊥OA于F,
同理证得△AOB≌△DFA,
∴OA=DF,
∴2b=4,
∴b=2;
综上,b的值为或或2,
故答案为:或或2.
三、解答题
12.解:(1)直线与轴交于点,与轴交于点,
,,
,,
;
(2)如图,
,,
,,
在中,,
点是线段的中点,
,
,
,
,
,
,
,即,
,
,
,
点的坐标为,
设直线的表达式为,将代入得:,解得:,
直线的表达式为;
(3)分别过点,点作的垂线,在直线下方截取,,连接,交于,
,,,,
、是等腰直角三角形,
,
,,
是等腰直角三角形,
过点,作轴于,轴于,
,,
,
,,
,
,,
,
点的坐标,
同理点的坐标,
,
点的坐标,,即,
综上,点的坐标为或或.
13.
解:(1)因为直线,
令x=0,则y=-4,令y=0,则x=-2,
,,
,,
△的面积;
(2)设A′B与x轴的交点为D,由题意可知D(2,0),
设直线A′B的解析式为y=kx-4,
把D(2,0)代入得0=2k-4,
解得k=2,
∴直线A′B的解析式为y=2x-4,
由,解得:或,
∴点A′的坐标是(3,2);
(3)若四边形为梯形,由于点在轴的正半轴.
①证明与不平行;
∵,在中,
令,则,
又,
则,
(由于在中,,即,
所以与不平行;
②当时,可得,
即,,
又,,
所以,
过作垂线,垂足为,过作垂线,垂足为,
∵BC=,AB=8,OC=2,
∴AM==,
∴BM==,
∴,
由旋转易得△,
,,
又,
∴,
,,
又点在反比例函数图象上,
.
14.(1)设直线OA的解析式为y=mx,将点A坐标代入,得
3m=4,
解得m=,
∴直线OA的解析式为y=x;
(2)如图,作AE⊥OA交直线y=kx于E,AD⊥x轴于D,EH⊥AD于H,
∵∠AOE=,∠OAE=,
∴∠AEO=∠AOE=,
∴OA=AE,
∵AD⊥x,,EH⊥AD,
∴∠ADO=∠AHE=∠OAE=,
∴∠OAD+∠HAE=∠HAE+∠AEH=,
∴∠OAD=∠AEH,
∴△OAD≌△AEH,
∴AH=OD=3,EH=AD=4,
∴HD=1,
∴点E的坐标为(7,1),
将点E的坐标代入y=kx中,得7k=1,
解得k=;
(3)∵点B在直线y=x上,纵坐标为1,
∴点B与点E重合,即B(7,1),
∵A(3,4),B(7,1),
∴AB=,
分三种情况:
①当AC=BC时,作CM⊥AB,则AM=BM,
∴M(5,2.5),
∵CM∥OA,
∴设直线CM的解析式为y=x+n,
∴,
解得n=,
∴y=x,
当y=0时,x=0,解得x=,
∴点C的坐标为(,0);
②当AB=AC=5时,
∵OA=AB,
∴AC=OA,
∴OC=6,
∴点C的坐标为(6,0);
③当AB=BC=5时,作BN⊥x轴于N,
∵ON=7,BN=1,BC=5,
∴CN==,
∴OC=ON+CN=,
∴点C的坐标为(,0),
综上,当△ABC是等腰三角形时,点C的坐标为(,0)或(6,0)或(,0).
.
15.
(1)①∵,,
∴∠BAC=60°,
∵AD平分,
∴∠FAG=∠EAG,
∵,
∴∠AGF=∠AGE=90°,
又∵AG=AG,
∴ AGF AGE,
∴FG=EG,
∴AD垂直平分FE,
∴DE=DF;
②∵在中,,,,
∴AB=2AC=12,
(a)当点F在线段AC上时,如图,
∵,,
∴AE=12-x,
∵ AGF AGE,
∴AF=AE=12-x,
∴y=6-(12-x)=x-6,
∵0<AF≤6,
∴0<12-x≤6,
∴6≤x<12;
(b)当点F在AC的延长线上时,如图,
∵,,
∴AF=AE=12-x,
∴y=12-x-6=6-x,
∵6<AF,
∴6<12-x,
∴0<x<6;
综上所述:y与x之间的函数解析式为:;
(2)①当是等腰三角形时,∠AFD是顶角,即FA=FD时,如图
∵,
∴AF=FD=6-y,
∵∠FAG=∠EAG=∠BAC=30°,
∴∠FDG=∠FAG=30°,
∵∠C=90°,∠ADC=90°-30°=60°,
∴∠CDF=30°,
∴DF=2CF,
∴6-y=2y,解得:y=2,
∴AF=6-2=4,
∴AE=AF=4,
∴BE=12-4=8;
②当是等腰三角形时,∠FAD是顶角,即FA=DA时,如图,
∵∠ACD=90°,∠CAD=30°,AC=6,
∴AD=2CD=2×(6÷)=4,
∴AE=AF=4,
∴BE=12-4;
③当是等腰三角形时,∠ADF是顶角,即DF=DA时,如图,
∵DC⊥AF,
∴CF=CA=6,
∴AF=12,
∴AE=AF=12,此时,点E与点B重合,舍去,
综上所述:BE=8或12-4.
16.解:(1)点D的横坐标为a,则点D(a,2a),
则AB=AD=2a,则点A、B、C的坐标分别为(a,0)、(3a,0)、(3a,2a),
故点A、B、C、D的坐标分别为(a,0)、(3a,0)、(3a,2a)、(a,2a);
(2)将点C的坐标代入y=kx得,2a=3ak,
解得k=;
(3)设AF=m,则点F(a,m),设直线OC旋转后交AD于点F,交CD于点E,
则直线OF的表达式为,
当y=2a时,y=,
解得x=,
故点E(,2a),
由题意得:S△DEF=S正方形ABCD=,
即,
解得:m=,
则函数的表达式为y==(3±)x.
17.(1)对于
当时,,则点的坐标为
设
∵
在中,,
则有
解得,即
∴点的坐标为
∵直线经过点
∴,解得
故直线的表达式为;
(2)点是点关于原点的对称点
点的坐标为
设直线上的点坐标为
则
由等腰三角形的定义,分以下三种情况:
①当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或
②当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或(与点重合,不能构成三角形,舍去)
③当时,是等腰三角形
则,解得
此时,点的坐标为
综上,点的坐标为点或.
18.(1)甲每小时施工:606=10(米),
故答案为:10
(2)当时,设y=kx,
将(2,30)代入,得2k=30,
解得k=15,
故答案为:y=15x;
(3)当时,甲每小时的工作量为10米;
乙每小时的工作量为: (米),
∴甲队比乙队每小时快10-5=5米,
故答案为:5;
(4)设铺设的每条彩色道砖路面的长度为a米,
由题意得: ,
解得a=110,
经检验,a=110是原方程的解,
故答案为:110.
19.解:(1)如图,过P作PM⊥x轴,垂足为M,
∵A(4,0),P(2,3),
∴S△POA==.
(2)如图,过P作PN⊥y轴,垂足为N,
∵B(0,6),P(m,n),
∴S ==.
∵P在线段AB上(不与点A、B重合)
∴0∴S关于m的函数解析式为S=3m,0(3)如图,设直线AB的解析式为y=kx+b,将A(4,0),B(0,6)代入,
,
解得, ,
∴直线AB的解析式为 ,
∴P(m, ).
∵S△BOP:S△POA=1:2,∴S△POA=2 S△BOP
①当m≤0,即点P在第二象限时,
根据题意得,
解得,m= -4,
∴P(-4,12),
设直线OP解析式为y=ax,将P点代入,
-4a=12,
解得,a= -3,
∴直线OP解析式为y= -3x;
②当0根据题意得,
解得,m= ,
∴P(,4),
设直线OP解析式为y=ax,将P点代入,
a=4,
解得,a= 3,
∴直线OP解析式为y= 3x;
③当m>4,即点P在第四象限时,
根据题意得,
解得,m= -4(不符合题意,舍去) .
综上所述,直线OP的解析式为:y=3x或y= -3x
20.(1)如图1中,
由题意线段PQ的“观察线”的解析式为y=0或y=2,
∵点A在直线y=0上,点B在直线y=2上,
∴点A,点B是直线PQ的“观察线”上的点,
故答案为A,B.
(2)如图2中,设直线y=x的下方的“观察线”MN交y轴于K,作KE⊥直线y=x,
由题意:EK=,
∵直线y=x与x轴的夹角为30°,
∴∠EOK=60°,
∴∠EKO=30°,
∴tan30°==,
∴OE=1,
∴OK=2OE=2,
∵MN∥直线y=x,
∴直线MN的解析式为y=x﹣2,
根据对称性可知在直线y=x上方的“观察线”PQ的解析式为y=x+2.
综上所述,直线y=x的“观察线”的解析式为y=x﹣2或y=x+2.
(3)如图3中,设点Q是MN的一个“最佳观察点”,点P是MN的中点.
当点Q在y轴的正半轴上时,连接PQ,则PQ垂直平分线线段MN.
在Rt△PQM中,PQ=,PM=3,
∴MQ==2,
∵M(0,﹣1),
OQ=2﹣1,
作PH⊥y轴于H.
在Rt△PQH中,∵tan∠PQH==,
∴∠PQH=60°,
∴∠QPH=30°,
∴QH=PQ=,PH=QH=,
∴OH=2﹣1﹣=﹣1,
∴P(﹣,﹣1),
∵PN=PM,
∴N(﹣3,3﹣1).
观察图象可知:设此时的另一个“最佳观察点”为Q′,按逆时针方向联结M、N及其所有“最佳观察点”,所围成的图形是菱形MQNQ′,这个菱形的周=8,这个菱形的面积=×6×2=6.
21.解:(1)过点C作x轴的垂线,交x轴于点H,
∵,
∴A(0,4),B(2,0),
∵BA=BC,
∴≌(ASA),
∴BH=AO=4,CH=OB=2,
∴C(6,2)
(2)如图,由题意可知点G(1,0),点E(1,2),
∵AB=BC=2,
∴,
∵,
∴,
而,
设M(1,a),则,
解的a=7,
则M(1,7) ;
(3)联结CM,CE,
由于点E(1,2),C(6,2),M(1,7),
则CE=5,EM=5,CM=,
可得:,
CE=EM,
∴是等腰直角三角形.
22.解:(1)令y=0,则x=4;令x=0,则y=3,
故点A的坐标为(4,0),点B的坐标为(0,3).
故答案为(4,0),(0,3);
(2)设OC=x,
∵直线CD垂直平分线段AB,
∴AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得
∴
∴设直线BC的解析式为y=kx+b,
则有
解得
∴直线BC的解析式为
(3)过点O作OM∥AB交直线BC于M.
∵OM∥AB,∴S△AOB=S△ABM,
∵直线AB的解析式为,OM∥AB,
∴直线OM的解析式为
由解得,∴M,
根据对称性可知,经过点O′(0,6)与直线AB平行的直线与直线BC的交点M′,也满足条件,易知BM′=BM,
设M′(m,n),则有
∴
∴M′
综上所述,满足条件的点M坐标为或.
23.(1)证明:∵EG⊥AM
∴∠BAM+∠ABG=90°,又∠CBF+∠ABG=90°
∴∠BAM=∠CBF
在△BAM和△CBF中,
∴△BAM≌△CBF
∴BM=CF
(2)解:作EH⊥CD于H,
由(1)得,△BAM≌△HEF,
∴HF=BM=2,
∴DF=4-2-x=2-x
24.(1)从左往右,从上往下依次填:(200-x)吨,(240-x)吨,(x+60)吨.
yA=20x+25(200-x)=5000-5x(0≤x≤200),
yB=15(240-x)+18(x+60)=3x+4680(0≤x≤200).
(2)当yA=yB,即5000-5x=3x+4680时,
解得:x=40,所以当x=40时,两村的运费一样多;
当yA>yB,即5000-5x>3x+4680时,
解得:x<40,所以当0≤x<40时,B村的运费较少;
当yA<yB,即5000-5x<3x+4680时,解得:x>40,
所以当40<x≤200时,A村的运费较少.
(3)由B村的柑橘运费不得超过4830元,得3x+4680≤4830,
解得:x≤50.
两村运费之和w=yA+yB=5000-5x+3x+4680=9680-2x.
∵-2<0,
∴w随x的增大而减小,
∴当x=50时,两村的运费之和最小,
∴调运方案为A村运往C仓库50吨柑橘,运往D仓库150吨柑橘,B村运往C仓库190吨柑橘,运往D仓库110吨柑橘,两村的费用之和最小,最小值为9680-2×50=9580(元).
25.解:(1)∵直线与直线: 平行,
∴设,
∵直线经过点,
∴,
∴,
∴,
当时,
,
解得,
∴.
(2)四边形ABCD是矩形.
∵,,
∴,
∵,,
∴,
∴,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵,,
∴BD=AC,
∴平行四边形ABCD是矩形.
(3)如图所示,
点E坐标为:,.
26.解:(1)当x=0时,y=4,
∴B(0,4),
当y=0时,即2x+4=0,
解得,x=-2,
∴A(-2,0),
∴OA=2,OB=4,
∵梯形AOBC的面积为10,
∴ .
解得,
∴点C(-3,4).
(2)设直线AC的表达式为(),
则,解得
∴直线AC的表达式为.
27.解:(1)由题意,得
笔记本型号 A B
数量(本) x 30-x
价格(元/本) 12 8
售价(元) 12x 8(30-x)
(2)由题意,得
12x+8(30-x)≤280,
解得:x≤10.
∴最多能购买A笔记本10本;
(3)设购买两种笔记本的总费用为W元,由题意,得
W=12x+8(30-x)=4x+240.
30-x<3x,
∴x>7.5.
∵k=4>0,
∴W随x的增大而增大,
∴x=8时,W最小=272元.
28.解: (1)如图1中,
∵一次函数y=-x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,
,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8-x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b则
,解得,
∴直线AE的解析式为y=-2x+6.
(2)由(1)可知OE=3,AE=,EB=5,
∵S△AEB= EB OA= AE BF,
∴BF=.
(3)如图2中,
在Rt△AOE中,,
∴AE=,
∵S△AEB= EB OA= AE BF,
∴BF=,
∴y=(0<x<8).
29.
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴
解得,
∴直线MN的解析式为y=-x+6
(3)
∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=-x+6上
∴设P(a,--a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-a+6-6)2=64
解得,a=±,则P2(-,),P3(,)
③当PB=BC时,(a-8)2+(-a+6-6)2=64
解得,a=,则-a+6=-
∴P4(,)
综上所述,符合条件的点P有:P1(4,3),P2(-,),P3(,),P4(,-)
30.(1)对于y=-x+6,
当x=0时,y=6;当y=0时,x=8,
∴OA=6,OB=8,
在Rt△AOB中,根据勾股定理得:AB=10,
则A(0,6),B(8,0);
(2)过点E作EG⊥AB,垂足为G
∵AE平分∠BAO,EO⊥AO,EG⊥AG,
∴EG=OE,
在Rt△AOE和Rt△AGE中,
∴Rt△AOE≌Rt△AGE(HL),
∴AG=AO,
设OE=EG=x,则有BE=8-x,BG=AB-AG=10-6=4,
在Rt△BEG中,EG=x,BG=4,BE=8-x,
根据勾股定理得:x2+42=(8-x)2,
解得:x=3,∴E(3,0),
设直线AE的表达式为y=kx+b(k≠0),
将A(0,6),E(3,0)代入y=kx+b得: ,解得
则直线AE的表达式为y=-2x+6;
(3)延长BF交y轴于点K,
∵AE平分∠BAO,
∴∠KAF=∠BAF,
又BF⊥AE,
∴∠AFK=∠AFB=90°
∵AF=AF
∴△AFK≌△AFB,
∴FK=FB,即F为KB的中点,
又∵△BOK为直角三角形,
∴OF= BK=BF,
∴△OFB为等腰三角形,
过点F作FH⊥OB,垂足为H(如图所示),
∵OF=BF,FH⊥OB,
∴OH=BH=4,
∴F点的横坐标为4,
设F(4,y),将F(4,y)代入y=-2x+6,得:y=-2,
FH=|-2|=2,
则S△OBF= OB FH= ×8×2=8.
一、单选题
1.如图,点、以及直线在的正方形网格中,每个小正方形的边长为单位1.在网格中建立直角坐标系后,、两点的坐标分别、,在直线上找一点使得最小,则点的坐标为( )
A. B. C. D.
2.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段OA、PB分别反映了小张、小王步行所走的路程S(千米)与时间t(分钟)的函数关系,根据图像提供的信息,小王比小张早到乙地的时间是( )分钟.
A.4 B.6 C.16 D.10
3.如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,点在线段上,轴于点,则周长的最小值为( ).
A. B. C.4 D.
4.如图所示,直线y=x+4与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,则周长的最小值是( )
A. B. C. D.
5.对于实数,定义符号其意义为:当时,;当时,.例如:,若关于的函数,则该函数的最大值是( )
A. B. C. D.
二、填空题
6.如图,在平面直角坐标系中,点A,,,…,都在直线上,点,,…都在直线上,在轴上,且……,以为直角边在两条直线内部作等腰直角三角形,在边上;再以为直角边在两条直线内部作等腰直角三角形,在边上;…如此做下去,则的面积用含有的代数式表示为__________.
7.如图,在直角坐标xoy系中,点A的坐标是(2,0)、点B的坐标是(0,2)、点C的坐标是(0,3),若直线CD的解析式为y=-x+3,则S△ABD为___________.
8.如图,在平面直角坐标系中,直线与轴交于点,与轴交点于,且,°,以为边长作等边三角形,过点作平行于轴,交直线于点,以为边长作等边三角行,过点作平行于轴,交直线于点,以为边长坐等三角形,…,则点的横坐标是___________.
9.在平面直角坐标系中,直线分别交x轴、y轴于C、A两点.将射线绕着点A顺时针旋转,得到射线.点D为上的动点,点B为上的动点,点C在的内部.
(1)周长的最小值是____________________;
(2)当的周长取得最小值,且时,的面积为__________.
10.如图,反比例函数的图象与直线()交于,两点(点在点左侧),过点作轴的垂线,垂足为点,连接,,图中阴影部分的面积为6,则的值为______.
11.如图,在平面直角坐标系中,点,射线轴,直线交线段于点B,交x轴于点A,D是射线上一点.若存在点D,使得恰为等腰直角三角形,则b的值为______.
三、解答题
12.在直角坐标平面中,任意线段的中点坐标可以用这条线段的两个端点的坐标来表示,若平面内点,点,则线段的中点坐标可以表示为,如图,直线与轴交于点,与轴交于点,点是线段的中点.
(1)求点的坐标
(2)点在轴上,且,求直线的表达式.
(3)在平面直角坐标系内,直线下方是否存在一点,使得是等腰直角三角形,若存在,请直接写出点的坐标,不存在,请说明理由.
13.已知,如图,在平面直角坐标系中,一次函数与轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,将△ABC绕着顶点B旋转后,点C的对应点C’落在y轴上,点A的对应点A’恰好落在反比例函数 的图像上.
(1)求的面积;
(2)如果的值为6 (即反比例函数为),求点的坐标;
(3)如果四边形是梯形,求的值.
14.如图,在直角坐标平面内,点是坐标原点,点坐标为,将直线绕点顺时针旋转后得到直线.
(1)求直线的表达式;
(2)求的值;
(3)在直线上有一点,其纵坐标为1.若轴上存在点,使是等腰三角形,请直接写出满足要求的点的坐标.
15.已知:如图,在中,,,,AD平分,交BC边于点D.点E是边AB上一动点(与点A、B不重合).过点E作,垂足为点G,与射线AC交于点F.
(1)当点F在边AC上时,
①求证:;
②设,,求y与x之间的函数解析式并写出定义域.
(2)当是等腰三角形时,求BE的长.
16.如图,正方形ABCD的顶点A、B落在x轴正半轴上,点C落在正比例函数y=kx(k>0)上,点D落在直线y=2x上,且点D的横坐标为a.
(1)直接写出A、B、C、D各点的坐标(用含a的代数式表示);
(2)求出k的值;
(3)将直线OC绕点O旋转,旋转后的直线将正方形ABCD的面积分成1:3两个部分,求旋转后得到的新直线解析式.
17.已知:如图,在直角坐标平面中,点在轴的负半轴上,直线经过点,与轴相交于点,点是点关于原点的对称点,过点的直线轴,交直线于点,如果.
(1)求直线的表达式;
(2)如果点在直线上,且是等腰三角形,请求出点的坐标.
18.浦东新区在创建文明城区的活动中,有两段长度相等的彩色道砖路面的铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设的彩色道砖路面的长度(米)与施工时间(时)之间关系的部分图像.请根据题意回答下列问题:
(1)甲队每小时施工_________米;
(2)乙队在时段内,与之间的函数关系式是_________;
(3)在时段内,甲队比乙队每小时快_________米;
(4)如果甲队施工速度不变,乙队在小时后,施工速度增加到米/时,结果两队同时完成了任务.则甲队从开始施工到完工所铺设的彩色道砖路面的长度为_________米.
19.如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
20.观摩、学习是我们生活的一部分,而在观摩中与展览品保持一定的距离是一种文明的表现.某学校数学业余学习小组在平面直角坐标系xOy有关研讨中,将到线段PQ所在的直线距离为的直线,称为直线PQ的“观察线”,并称观察线上到P、Q两点距离和最小的点L为线段PQ的“最佳观察点”.
(1)如果P(1,),Q(4,),那么在点A(1,0),B(,2),C(,3)中,处在直线PQ的“观察线”上的是点 ;
(2)求直线y=x的“观察线”的表达式;
(3)若M(0,﹣1),N在第二象限,且MN=6,当MN的一个“最佳观察点”在y轴正半轴上时,直接写出点N的坐标;并按逆时针方向联结M、N及其所有“最佳观察点”,直接写出联结所围成的多边形的周长和面积.
21.已知一次函数的图像与轴、轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
(1)求点的坐标;
(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得,求点M的坐标;
(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
22.如图,已知直线y=﹣x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.
23.如题,,点是边的中点,点是边上的一个动点,作交于点,的延长线交线段于点.
(1)如图①,当点于点重合时,求证:;
(2)设,梯形的面积为,求与的函数解析式,并写出定义域.
24.某地A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元、25元,从B村运往C、D两处的费用分别为每吨15元、18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元、yB元.
(1)请填写下表,并求出yA、yB与x之间的函数表达式;
(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
25.如图,在平面直角坐标系中,直线经过点且与直线: 平行,直线与轴、轴分别交于点B、C.
(1)求直线l1的表达式及其与轴的交点D的坐标;
(2)判断四边形ABCD是什么四边形?并证明你的结论;
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.
26.如图,已知一次函数的图像与x轴、轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
27.某校八年级举行“生活中的数学”数学小论文比赛活动,购买A、B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元,根据比赛设奖情况,需要购买两种笔记本共30本,若学校决定购买本次笔记本所需资金不能超过280元,设买A种笔记本x本.
(1)根据题意完成以下表格(用含x的代数式表示)
(2)那么最多能购买A笔记本多少本?
(3)若购买B笔记本的数量要小于A笔记本的数量的3倍,则购买这两种笔记本各多少本时,费用最少,最少的费用是多少元?
28.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
29.如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
30.已知一次函数y=-x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
答案
一、单选题
1.B
【分析】根据题意建立直角坐标系,作B关于l的对称点C,连接AC,则AC与l的交点即为所求点P,接着写出直线AC与直线l的函数解析式,联立得到关于P点坐标x、y的二元一次方程组,解方程组即可得到P点坐标.
【详解】解:如图,由题意可建立直角坐标系,作B关于l的对称点C,连接AC,则AC与l的交点即为所求点P,
由图可写出l的函数解析式为y=-1,
设直线AC的函数为y=kx+b,则把A、C坐标代入可得:,
解之可得:k=-1,b=1,
∴直线AC的函数为y=-x+1,
∴有,解之得:x=2,y=-1,
∴P点坐标为(2,-1),
故选B .
2.B
【分析】由函数图象求出、解析式,再把代入解析式就可以求出小张、小王所用时间.
【详解】解:由图象可知:
设的解析式为:,
经过点,
,
得,
函数解析式为:①,
把代入①得:,
解得:,
小张到达乙地所用时间为96(分钟);
设的解析式为:,
,
解得:,
的解析式为:②,
把代入②得:,
解得:,
则小王到达乙地的时间为小张出发后90(分钟),
小王比小张早到(分钟),
故选:B.
3.B
【分析】先根据一次函数的解析式可得,设点P的坐标为,从而可得,再根据三角形的周长公式可得周长为,然后根据垂线段最短可得当时,OP取得最小值,最后利用等腰直角三角形的判定与性质求出OP的最小值即可得.
【详解】对于一次函数,
当时,,解得,即,,
当时,,即,,
由题意,设点P的坐标为,
则,
因此,周长为,
要使周长最小,则只需OP取得最小值,
由垂线段最短可知,当时,OP取得最小值,
又,
是等腰直角三角形,,
此时,
周长的最小值为,
故选:B.
4.D
【分析】如图(见解析),先根据轴对称的性质可得,再根据三角形的周长公式、两点之间线段最短可得周长的最小值为FG的长,然后根据直线AB的解析式求出点B的坐标,从而可得点C、G的坐标,最后根据等腰直角三角形的判定与性质可得点F的坐标,据此利用两点之间的距离公式即可得出答案.
【详解】如图,作点C关于AB的对称点F,关于AO的对称点G,连接DF、EG、BF,
由轴对称的性质得:,
周长为,
由两点之间线段最短得:当点在同一直线上时,取得最小值,最小值为FG的长,
对于一次函数,
当时,,解得,即,
当时,,即,
,
点C为OB的中点,
,
点G为点C关于AO的对称点,
,
又,
,
,
,
,
是等腰直角三角形,,即轴,
,
则,
即周长的最小值是,
故选:D.
5.C
二、填空题
6.
【分析】根据点A,,,…,都在直线上先求出,再根据点,,…都在直线上,求出,由在轴上,且……,以为直角边在两条直线内部作等腰直角三角形,得到的横坐标为2,同理依次类推,得出 ,,,最后算出面积即可.
【详解】解:当x=0时,,,
∴,
∵,
∴的横坐标为2,
∴,
∴,
∵,
∴的横坐标为,
∴,
∴,
∵,
∴的横坐标为,
∴,
∴,
∴,,,
∴ ,,,
∴=,
=
=,
故答案为:.
7.1
【解析】分析:先求出直线AB的解析式,根据直线AB与直线CD的k值相等可得出它们平行,根据平行线间的距离处处相等可得出,即可得出答案.
详解:设直线AB的解析式为,
∵A的坐标是(2,0)、点B的坐标是(0,2)、
∴,
解得,
∴直线AB的解析式为,
∵直线CD的解析式为y=-x+3,
∴AB//CD,
∴,
∵点A的坐标是(2,0)、点B的坐标是(0,2)、点C的坐标是(0,3),
∵BC=1,AO=2,
∴,
∴
故答案为:1.
8.
【分析】过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为,,A2的横坐标为, A3的横坐标为,进而得到An的横坐标为,据此可得点A10的横坐标.
【详解】解:如图所示,过A1作A1A⊥OB1于A,则OA=OB1=,
即A1的横坐标为=,
∵°,
∴∠OB1D=30°,
∵A1B2//x轴,
∴∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=A1B2=1,
即A2的横坐标为+1=,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=A2B3=2,
即A3的横坐标为+1+2=,
同理可得,A4的横坐标为+1+2+4=,
由此可得,An的横坐标为,
∴点A10的横坐标是,
故答案为.
9.
【分析】(1)可作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.连接C1C2.利用两点之间线段最短,可得到当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
(2)根据(1)的作图可知四边形AC1CC2的对角互补,结合轴对称可得∠BCD=90°.利用勾股定理得到CB2+CD2=BD2=()2,因为CB+CD=4﹣,可推出CB CD的值,进而求出三角形的面积.
【详解】(1)∵直线y=与x轴、y轴分别交于C、A两点,把y=0代入,解得x=2,把x=0代入,解得y=2,
∴点C的坐标为(2,0),点A的坐标为(0,2).
∴AC=4.
作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.由轴对称的性质,可知CD=C1D,CB=C2B.
∴CB+BD+CD=C2B+BD+C1D=C1C2连接AC1、AC2,
可得∠C1AD=∠CAD,∠C2AB=∠CAB,AC1=AC2=AC=4.
∵∠DAB=45°,
∴∠C1AC2=90°.
连接C1C2.,
∵两点之间线段最短,
∴当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
∴△BCD的周长的最小值为4.
故答案为:4.
(2)根据(1)的作图可知四边形AECF的对角互补,其中∠DAB=45°,因此,∠C2CC1=135°.
即∠BCC2+∠DCC1+∠BCD=135°,
∴2∠BCC2+2∠DCC1+2∠BCD=270°①,
∵∠BC2C=∠BCC2,∠DCC1=∠DC1C,∠BC2C+∠DC1C+∠BCC2+∠DCC1+∠BCD=180°,
∴2∠BCC2+2∠DCC1+∠BCD=180°②,
①-②得,∠BCD=90°.
∴CB2+CD2=BD2=()2=,
∵CB+CD=4﹣,
(CB+CD)2=CB2+CD2+2CB CD,
∴2CB CD=(CB+CD)2-(CB2+CD2)=
∴.
故答案为:
10.
【分析】首先由已知得到S△BFG=2S△OEC,从而可得A、B横坐标的关系,再设A、B坐标代入y= x+m,即可求解.
【详解】解:过点A、B分别作y轴和x轴的垂线,垂足分别为R、F,
设点M是AB的中点,
由,整理得:x2 mx+6=0,
由题意可得x2 mx+6=0有两个不相等的实数根分别设为x1,x2,
则x1+x2=m,y1+y2= x1+m x2+m=m,
则点M的坐标为(m,m),
设直线AB交x轴于点G,交y轴于点H,
对于y= x+m,令x=0,则y=m,令y=0,则x=m,
∴点G、H的坐标分别为(m,0)、(0,m),
则点HG中点的坐标为(m,m),
即点M也为GH的中点,故AH=BG,
∵AR∥x轴,
∴∠HAR=∠BGF,
∵∠HRA=∠BFG=90°,
∴△HRA≌△BFG(AAS),
∴AR=OC=FG,
∴S△HRA=S△BFG,
∵S△AEO+S△OCE+S△OCE+S四边形ECFB=|k|+|k|=6,
而阴影部分的面积=S△AEO+S四边形EBFC+S△BFG=6,
∴S△BFG=2S△OEC,
即2××CO EC=×BF FG,
而OC=FG,
∴EC=BF,
即EC是△OBF的中位线,
故设点A的坐标为(t, ),则点B(2t,),
将点A、B的坐标代入一次函数表达式得:,解得(不合题意的值已舍去),
故答案为:.
11.或或2
【分析】分三种情况讨论:①当∠ABD=90°时,证得△DBC≌△BAO,得出BC=OA,即4-b=2b,求得b=;②当∠ADB=90°时,作AF⊥CE于F,同理证得△BDC≌△DAF,得出BC=DF,即2b-4=4-b,求得b=;③当∠DAB=90°时,作DF⊥OA于F,同理证得△AOB≌△DFA,得出OA=DF,即2b=4,解得b=2.
【详解】解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,
∴∠DBC=∠BAO,
由直线交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
∵点C(0,4),
∴OC=4,
∴BC=4-b,
在△DBC和△BAO中,
,
∴△DBC≌△BAO(AAS),
∴BC=OA,
即4-b=2b,
∴b=,
②当∠ADB=90°时,如图2,作AF⊥CE于F,
同理证得△BDC≌△DAF,
∴CD=AF=4,BC=DF,
∵OB=b,OA=2b,
∴BC=DF=2b-4,
∵BC=4-b,
∴2b-4=4-b,
∴b=;
③当∠DAB=90°时,如图3,作DF⊥OA于F,
同理证得△AOB≌△DFA,
∴OA=DF,
∴2b=4,
∴b=2;
综上,b的值为或或2,
故答案为:或或2.
三、解答题
12.解:(1)直线与轴交于点,与轴交于点,
,,
,,
;
(2)如图,
,,
,,
在中,,
点是线段的中点,
,
,
,
,
,
,
,即,
,
,
,
点的坐标为,
设直线的表达式为,将代入得:,解得:,
直线的表达式为;
(3)分别过点,点作的垂线,在直线下方截取,,连接,交于,
,,,,
、是等腰直角三角形,
,
,,
是等腰直角三角形,
过点,作轴于,轴于,
,,
,
,,
,
,,
,
点的坐标,
同理点的坐标,
,
点的坐标,,即,
综上,点的坐标为或或.
13.
解:(1)因为直线,
令x=0,则y=-4,令y=0,则x=-2,
,,
,,
△的面积;
(2)设A′B与x轴的交点为D,由题意可知D(2,0),
设直线A′B的解析式为y=kx-4,
把D(2,0)代入得0=2k-4,
解得k=2,
∴直线A′B的解析式为y=2x-4,
由,解得:或,
∴点A′的坐标是(3,2);
(3)若四边形为梯形,由于点在轴的正半轴.
①证明与不平行;
∵,在中,
令,则,
又,
则,
(由于在中,,即,
所以与不平行;
②当时,可得,
即,,
又,,
所以,
过作垂线,垂足为,过作垂线,垂足为,
∵BC=,AB=8,OC=2,
∴AM==,
∴BM==,
∴,
由旋转易得△,
,,
又,
∴,
,,
又点在反比例函数图象上,
.
14.(1)设直线OA的解析式为y=mx,将点A坐标代入,得
3m=4,
解得m=,
∴直线OA的解析式为y=x;
(2)如图,作AE⊥OA交直线y=kx于E,AD⊥x轴于D,EH⊥AD于H,
∵∠AOE=,∠OAE=,
∴∠AEO=∠AOE=,
∴OA=AE,
∵AD⊥x,,EH⊥AD,
∴∠ADO=∠AHE=∠OAE=,
∴∠OAD+∠HAE=∠HAE+∠AEH=,
∴∠OAD=∠AEH,
∴△OAD≌△AEH,
∴AH=OD=3,EH=AD=4,
∴HD=1,
∴点E的坐标为(7,1),
将点E的坐标代入y=kx中,得7k=1,
解得k=;
(3)∵点B在直线y=x上,纵坐标为1,
∴点B与点E重合,即B(7,1),
∵A(3,4),B(7,1),
∴AB=,
分三种情况:
①当AC=BC时,作CM⊥AB,则AM=BM,
∴M(5,2.5),
∵CM∥OA,
∴设直线CM的解析式为y=x+n,
∴,
解得n=,
∴y=x,
当y=0时,x=0,解得x=,
∴点C的坐标为(,0);
②当AB=AC=5时,
∵OA=AB,
∴AC=OA,
∴OC=6,
∴点C的坐标为(6,0);
③当AB=BC=5时,作BN⊥x轴于N,
∵ON=7,BN=1,BC=5,
∴CN==,
∴OC=ON+CN=,
∴点C的坐标为(,0),
综上,当△ABC是等腰三角形时,点C的坐标为(,0)或(6,0)或(,0).
.
15.
(1)①∵,,
∴∠BAC=60°,
∵AD平分,
∴∠FAG=∠EAG,
∵,
∴∠AGF=∠AGE=90°,
又∵AG=AG,
∴ AGF AGE,
∴FG=EG,
∴AD垂直平分FE,
∴DE=DF;
②∵在中,,,,
∴AB=2AC=12,
(a)当点F在线段AC上时,如图,
∵,,
∴AE=12-x,
∵ AGF AGE,
∴AF=AE=12-x,
∴y=6-(12-x)=x-6,
∵0<AF≤6,
∴0<12-x≤6,
∴6≤x<12;
(b)当点F在AC的延长线上时,如图,
∵,,
∴AF=AE=12-x,
∴y=12-x-6=6-x,
∵6<AF,
∴6<12-x,
∴0<x<6;
综上所述:y与x之间的函数解析式为:;
(2)①当是等腰三角形时,∠AFD是顶角,即FA=FD时,如图
∵,
∴AF=FD=6-y,
∵∠FAG=∠EAG=∠BAC=30°,
∴∠FDG=∠FAG=30°,
∵∠C=90°,∠ADC=90°-30°=60°,
∴∠CDF=30°,
∴DF=2CF,
∴6-y=2y,解得:y=2,
∴AF=6-2=4,
∴AE=AF=4,
∴BE=12-4=8;
②当是等腰三角形时,∠FAD是顶角,即FA=DA时,如图,
∵∠ACD=90°,∠CAD=30°,AC=6,
∴AD=2CD=2×(6÷)=4,
∴AE=AF=4,
∴BE=12-4;
③当是等腰三角形时,∠ADF是顶角,即DF=DA时,如图,
∵DC⊥AF,
∴CF=CA=6,
∴AF=12,
∴AE=AF=12,此时,点E与点B重合,舍去,
综上所述:BE=8或12-4.
16.解:(1)点D的横坐标为a,则点D(a,2a),
则AB=AD=2a,则点A、B、C的坐标分别为(a,0)、(3a,0)、(3a,2a),
故点A、B、C、D的坐标分别为(a,0)、(3a,0)、(3a,2a)、(a,2a);
(2)将点C的坐标代入y=kx得,2a=3ak,
解得k=;
(3)设AF=m,则点F(a,m),设直线OC旋转后交AD于点F,交CD于点E,
则直线OF的表达式为,
当y=2a时,y=,
解得x=,
故点E(,2a),
由题意得:S△DEF=S正方形ABCD=,
即,
解得:m=,
则函数的表达式为y==(3±)x.
17.(1)对于
当时,,则点的坐标为
设
∵
在中,,
则有
解得,即
∴点的坐标为
∵直线经过点
∴,解得
故直线的表达式为;
(2)点是点关于原点的对称点
点的坐标为
设直线上的点坐标为
则
由等腰三角形的定义,分以下三种情况:
①当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或
②当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或(与点重合,不能构成三角形,舍去)
③当时,是等腰三角形
则,解得
此时,点的坐标为
综上,点的坐标为点或.
18.(1)甲每小时施工:606=10(米),
故答案为:10
(2)当时,设y=kx,
将(2,30)代入,得2k=30,
解得k=15,
故答案为:y=15x;
(3)当时,甲每小时的工作量为10米;
乙每小时的工作量为: (米),
∴甲队比乙队每小时快10-5=5米,
故答案为:5;
(4)设铺设的每条彩色道砖路面的长度为a米,
由题意得: ,
解得a=110,
经检验,a=110是原方程的解,
故答案为:110.
19.解:(1)如图,过P作PM⊥x轴,垂足为M,
∵A(4,0),P(2,3),
∴S△POA==.
(2)如图,过P作PN⊥y轴,垂足为N,
∵B(0,6),P(m,n),
∴S ==.
∵P在线段AB上(不与点A、B重合)
∴0
,
解得, ,
∴直线AB的解析式为 ,
∴P(m, ).
∵S△BOP:S△POA=1:2,∴S△POA=2 S△BOP
①当m≤0,即点P在第二象限时,
根据题意得,
解得,m= -4,
∴P(-4,12),
设直线OP解析式为y=ax,将P点代入,
-4a=12,
解得,a= -3,
∴直线OP解析式为y= -3x;
②当0
解得,m= ,
∴P(,4),
设直线OP解析式为y=ax,将P点代入,
a=4,
解得,a= 3,
∴直线OP解析式为y= 3x;
③当m>4,即点P在第四象限时,
根据题意得,
解得,m= -4(不符合题意,舍去) .
综上所述,直线OP的解析式为:y=3x或y= -3x
20.(1)如图1中,
由题意线段PQ的“观察线”的解析式为y=0或y=2,
∵点A在直线y=0上,点B在直线y=2上,
∴点A,点B是直线PQ的“观察线”上的点,
故答案为A,B.
(2)如图2中,设直线y=x的下方的“观察线”MN交y轴于K,作KE⊥直线y=x,
由题意:EK=,
∵直线y=x与x轴的夹角为30°,
∴∠EOK=60°,
∴∠EKO=30°,
∴tan30°==,
∴OE=1,
∴OK=2OE=2,
∵MN∥直线y=x,
∴直线MN的解析式为y=x﹣2,
根据对称性可知在直线y=x上方的“观察线”PQ的解析式为y=x+2.
综上所述,直线y=x的“观察线”的解析式为y=x﹣2或y=x+2.
(3)如图3中,设点Q是MN的一个“最佳观察点”,点P是MN的中点.
当点Q在y轴的正半轴上时,连接PQ,则PQ垂直平分线线段MN.
在Rt△PQM中,PQ=,PM=3,
∴MQ==2,
∵M(0,﹣1),
OQ=2﹣1,
作PH⊥y轴于H.
在Rt△PQH中,∵tan∠PQH==,
∴∠PQH=60°,
∴∠QPH=30°,
∴QH=PQ=,PH=QH=,
∴OH=2﹣1﹣=﹣1,
∴P(﹣,﹣1),
∵PN=PM,
∴N(﹣3,3﹣1).
观察图象可知:设此时的另一个“最佳观察点”为Q′,按逆时针方向联结M、N及其所有“最佳观察点”,所围成的图形是菱形MQNQ′,这个菱形的周=8,这个菱形的面积=×6×2=6.
21.解:(1)过点C作x轴的垂线,交x轴于点H,
∵,
∴A(0,4),B(2,0),
∵BA=BC,
∴≌(ASA),
∴BH=AO=4,CH=OB=2,
∴C(6,2)
(2)如图,由题意可知点G(1,0),点E(1,2),
∵AB=BC=2,
∴,
∵,
∴,
而,
设M(1,a),则,
解的a=7,
则M(1,7) ;
(3)联结CM,CE,
由于点E(1,2),C(6,2),M(1,7),
则CE=5,EM=5,CM=,
可得:,
CE=EM,
∴是等腰直角三角形.
22.解:(1)令y=0,则x=4;令x=0,则y=3,
故点A的坐标为(4,0),点B的坐标为(0,3).
故答案为(4,0),(0,3);
(2)设OC=x,
∵直线CD垂直平分线段AB,
∴AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得
∴
∴设直线BC的解析式为y=kx+b,
则有
解得
∴直线BC的解析式为
(3)过点O作OM∥AB交直线BC于M.
∵OM∥AB,∴S△AOB=S△ABM,
∵直线AB的解析式为,OM∥AB,
∴直线OM的解析式为
由解得,∴M,
根据对称性可知,经过点O′(0,6)与直线AB平行的直线与直线BC的交点M′,也满足条件,易知BM′=BM,
设M′(m,n),则有
∴
∴M′
综上所述,满足条件的点M坐标为或.
23.(1)证明:∵EG⊥AM
∴∠BAM+∠ABG=90°,又∠CBF+∠ABG=90°
∴∠BAM=∠CBF
在△BAM和△CBF中,
∴△BAM≌△CBF
∴BM=CF
(2)解:作EH⊥CD于H,
由(1)得,△BAM≌△HEF,
∴HF=BM=2,
∴DF=4-2-x=2-x
24.(1)从左往右,从上往下依次填:(200-x)吨,(240-x)吨,(x+60)吨.
yA=20x+25(200-x)=5000-5x(0≤x≤200),
yB=15(240-x)+18(x+60)=3x+4680(0≤x≤200).
(2)当yA=yB,即5000-5x=3x+4680时,
解得:x=40,所以当x=40时,两村的运费一样多;
当yA>yB,即5000-5x>3x+4680时,
解得:x<40,所以当0≤x<40时,B村的运费较少;
当yA<yB,即5000-5x<3x+4680时,解得:x>40,
所以当40<x≤200时,A村的运费较少.
(3)由B村的柑橘运费不得超过4830元,得3x+4680≤4830,
解得:x≤50.
两村运费之和w=yA+yB=5000-5x+3x+4680=9680-2x.
∵-2<0,
∴w随x的增大而减小,
∴当x=50时,两村的运费之和最小,
∴调运方案为A村运往C仓库50吨柑橘,运往D仓库150吨柑橘,B村运往C仓库190吨柑橘,运往D仓库110吨柑橘,两村的费用之和最小,最小值为9680-2×50=9580(元).
25.解:(1)∵直线与直线: 平行,
∴设,
∵直线经过点,
∴,
∴,
∴,
当时,
,
解得,
∴.
(2)四边形ABCD是矩形.
∵,,
∴,
∵,,
∴,
∴,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵,,
∴BD=AC,
∴平行四边形ABCD是矩形.
(3)如图所示,
点E坐标为:,.
26.解:(1)当x=0时,y=4,
∴B(0,4),
当y=0时,即2x+4=0,
解得,x=-2,
∴A(-2,0),
∴OA=2,OB=4,
∵梯形AOBC的面积为10,
∴ .
解得,
∴点C(-3,4).
(2)设直线AC的表达式为(),
则,解得
∴直线AC的表达式为.
27.解:(1)由题意,得
笔记本型号 A B
数量(本) x 30-x
价格(元/本) 12 8
售价(元) 12x 8(30-x)
(2)由题意,得
12x+8(30-x)≤280,
解得:x≤10.
∴最多能购买A笔记本10本;
(3)设购买两种笔记本的总费用为W元,由题意,得
W=12x+8(30-x)=4x+240.
30-x<3x,
∴x>7.5.
∵k=4>0,
∴W随x的增大而增大,
∴x=8时,W最小=272元.
28.解: (1)如图1中,
∵一次函数y=-x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,
,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8-x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b则
,解得,
∴直线AE的解析式为y=-2x+6.
(2)由(1)可知OE=3,AE=,EB=5,
∵S△AEB= EB OA= AE BF,
∴BF=.
(3)如图2中,
在Rt△AOE中,,
∴AE=,
∵S△AEB= EB OA= AE BF,
∴BF=,
∴y=(0<x<8).
29.
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴
解得,
∴直线MN的解析式为y=-x+6
(3)
∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=-x+6上
∴设P(a,--a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-a+6-6)2=64
解得,a=±,则P2(-,),P3(,)
③当PB=BC时,(a-8)2+(-a+6-6)2=64
解得,a=,则-a+6=-
∴P4(,)
综上所述,符合条件的点P有:P1(4,3),P2(-,),P3(,),P4(,-)
30.(1)对于y=-x+6,
当x=0时,y=6;当y=0时,x=8,
∴OA=6,OB=8,
在Rt△AOB中,根据勾股定理得:AB=10,
则A(0,6),B(8,0);
(2)过点E作EG⊥AB,垂足为G
∵AE平分∠BAO,EO⊥AO,EG⊥AG,
∴EG=OE,
在Rt△AOE和Rt△AGE中,
∴Rt△AOE≌Rt△AGE(HL),
∴AG=AO,
设OE=EG=x,则有BE=8-x,BG=AB-AG=10-6=4,
在Rt△BEG中,EG=x,BG=4,BE=8-x,
根据勾股定理得:x2+42=(8-x)2,
解得:x=3,∴E(3,0),
设直线AE的表达式为y=kx+b(k≠0),
将A(0,6),E(3,0)代入y=kx+b得: ,解得
则直线AE的表达式为y=-2x+6;
(3)延长BF交y轴于点K,
∵AE平分∠BAO,
∴∠KAF=∠BAF,
又BF⊥AE,
∴∠AFK=∠AFB=90°
∵AF=AF
∴△AFK≌△AFB,
∴FK=FB,即F为KB的中点,
又∵△BOK为直角三角形,
∴OF= BK=BF,
∴△OFB为等腰三角形,
过点F作FH⊥OB,垂足为H(如图所示),
∵OF=BF,FH⊥OB,
∴OH=BH=4,
∴F点的横坐标为4,
设F(4,y),将F(4,y)代入y=-2x+6,得:y=-2,
FH=|-2|=2,
则S△OBF= OB FH= ×8×2=8.
