沪教版八年级数学下册试题 第22章《四边形》复习题(含解析)
文档属性
| 名称 | 沪教版八年级数学下册试题 第22章《四边形》复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览



文档简介
第22章《四边形》复习题
一.选择题
1.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
2.已知向量、满足||=||,则( )
A.= B.=﹣
C.∥ D.以上都有可能
3.已知点C是线段AB的中点,下列结论中,正确的是( )
A. B. C. D.
4.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
5.下列判断不正确的是( )
A.如果=,那么||=||
B.+=+
C.如果非零向量=k (k≠0),那么与平行或共线
D.+=0
6.如果一个正多边形的每一个外角都是45°,那么这个正多边形的内角和为( )
A.360° B.720° C.1080° D.1440°
7.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
二.填空题
8.如果一个多边形的每个外角都是60°,那么这个多边形内角和的度数为 .
9.一个多边形的内角和为1440°,则这个多边形是 边形.
10.已知:在平行四边形ABCD中,设=,=,那么= (用向量、的式子表示).
11.已知一个梯形的中位线长为5cm,其中一条底边的长为6cm,那么该梯形的另一条底边的长是 cm.
12.菱形ABCD中,已知AB=4,∠B=60°,那么BD的长是 .
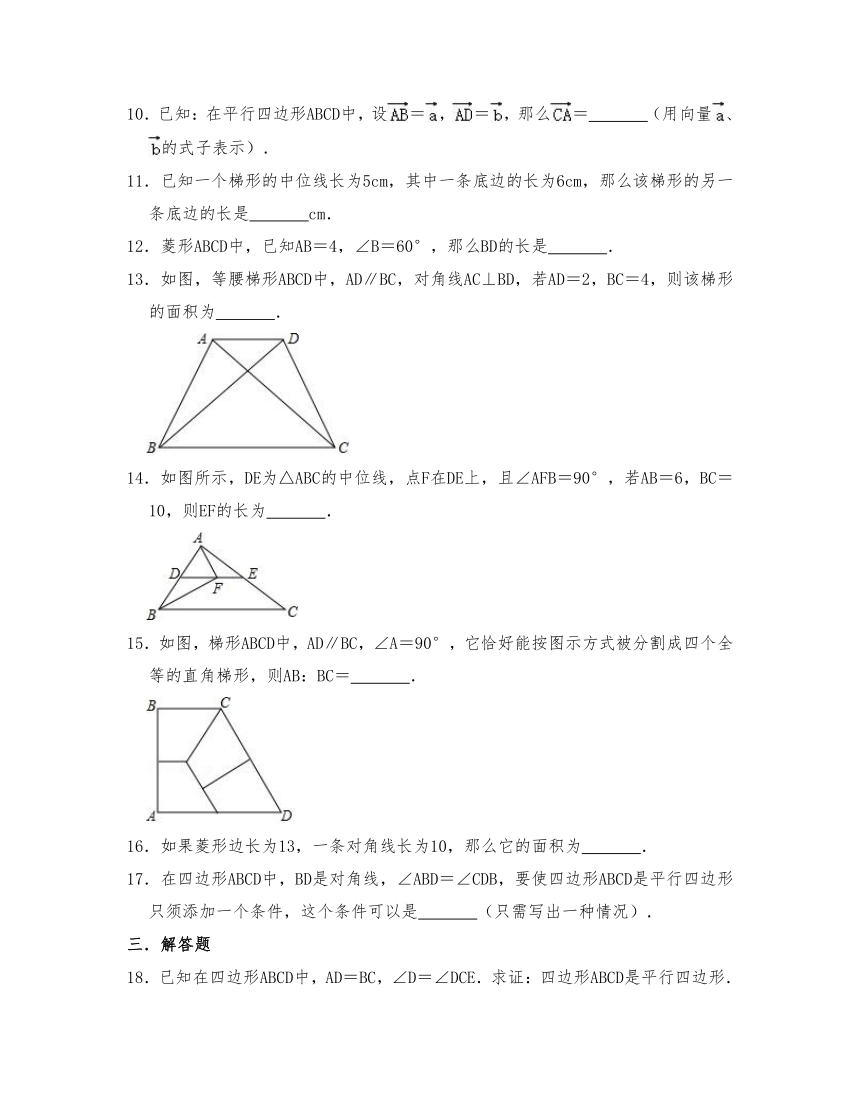
13.如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=2,BC=4,则该梯形的面积为 .
14.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为 .
15.如图,梯形ABCD中,AD∥BC,∠A=90°,它恰好能按图示方式被分割成四个全等的直角梯形,则AB:BC= .
16.如果菱形边长为13,一条对角线长为10,那么它的面积为 .
17.在四边形ABCD中,BD是对角线,∠ABD=∠CDB,要使四边形ABCD是平行四边形只须添加一个条件,这个条件可以是 (只需写出一种情况).
三.解答题
18.已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.
19.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.
求证:四边形ABCD是正方形;
20.如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
21.如图,已知△ABC中,点D为边AC的中点,设,,
(1)试用向量,表示下列向量:= ;= ;
(2)求作:、.
(保留作图痕迹,不要求写作法,写出结果).
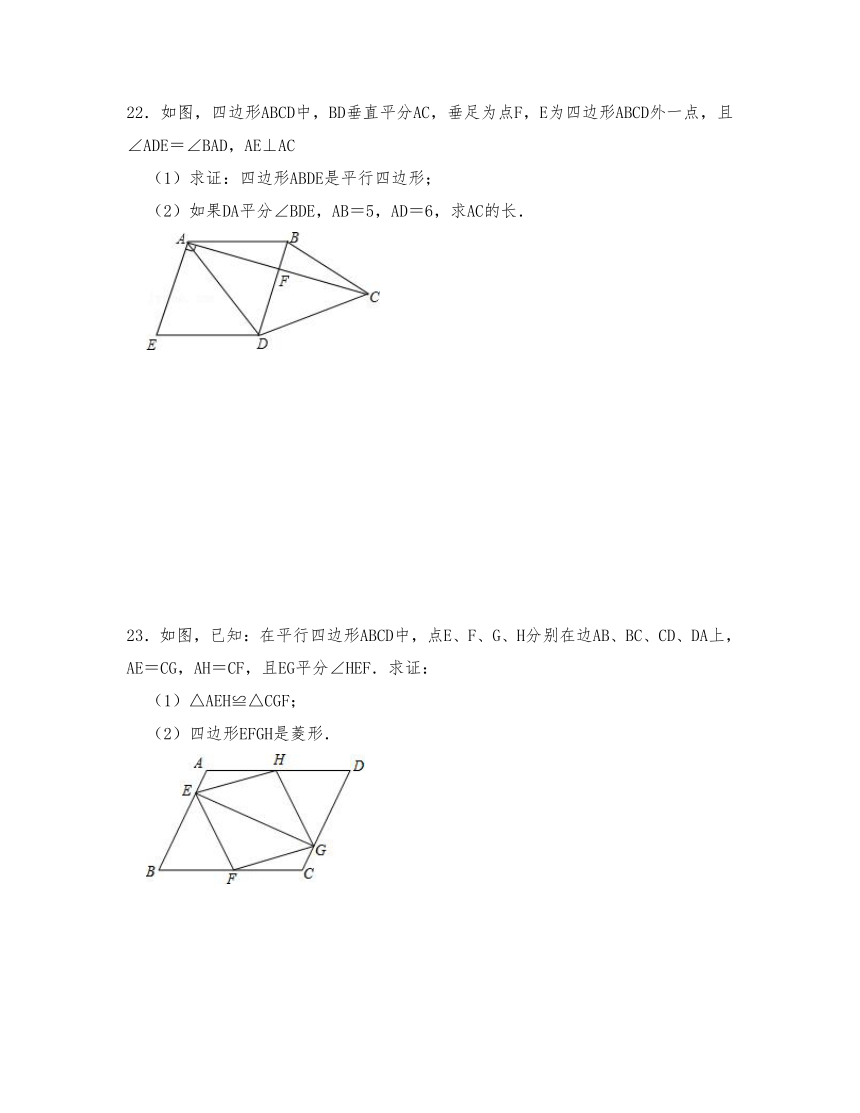
22.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
23.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
24.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当线段AB与线段AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
25.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
26.如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,EG∥AC.
(1)求证:FG∥AB;
(2)设=,=,请用向量、表示.
27.已知:如图,点E、G在平行四边形ABCD的边AD上,EG=ED,延长CE到点F,使得EF=EC.求证:AF∥BG.
28.如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(﹣6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
(1)求点D的坐标;
(2)若点N是平面内任一点,在x轴上是否存在点M,使M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
29.在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AB=8,BC=14,点E、F分别在边AB、CD上,EF∥AD,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
(1)求边AD的长;
(2)如图,当点P在梯形ABCD内部时,求y关于x的函数解析式,并写出定义域;
(3)如果MN的长为2,求梯形AEFD的面积.
30.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
答案
一.选择题
1.
【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.
【解答】解:如图所示:∵AB∥CD,
∴∠B+∠C=180°,
当∠A=∠C时,则∠A+∠B=180°,
故AD∥BC,
则四边形ABCD是平行四边形.
故选:C.
2.
【分析】利用单位向量的定义和性质直接判断即可.
【解答】解:若向量、满足||=||,
可得:=,或=﹣,或∥,
故选:D.
3.
【分析】根据题意画出图形,因为点C是线段AB的中点,所以根据线段中点的定义解答.
【解答】解:A、=,故本选项错误;
B、=,故本选项正确;
C、+=,故本选项错误;
D、+=,故本选项错误.
故选:B.
4.
【分析】根据多边形的内角和公式(n﹣2) 180°和外角和定理列出方程,然后求解即可.
【解答】解:设多边形的边数为n,
由题意得,(n﹣2) 180°=2×360°,
解得n=6,
所以,这个多边形是六边形.
故选:D.
5.
【分析】根据模的定义,可确定A正确;根据平面向量的交换律,可判定B正确,又由如果非零向量非零向量=k (k≠0),那么∥,可得C正确;利用相反向量的知识,可判定D错误.
【解答】解:A、如果=,那么||=||,故此选项正确;
B、+=+,故本选项正确;
C、如果非零向量=k (k≠0),那么与平行或共线,故此选项正确;
D、+=,故此选项错误;
故选:D.
6.
【分析】多边形的外角和是360度,即可得到外角的个数,即多边形的边数.根据多边形的内角和定理即可求解.
【解答】解:多边形的边数是:360÷45=8.
则内角和是:(8﹣2)×180°=1080°.
故选:C.
7.
【分析】由平行四边形的判定与性质、矩形的判定分别对各个选项进行判断即可.
【解答】解:A、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵AD∥BC,
∴∠A+∠B=∠C+∠D=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,AB=CD,故选项C符合题意;
D、∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴AB⊥AD,AB⊥BC,AB的长为AD、BC间的距离,
又∵AB=CD,
∴CD⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形,故选项D不符合题意;
故选:C.
二.填空题
8.
【分析】根据正多边形的性质,边数等于360°除以每一个外角的度数,然后利用多边形的内角和公式计算内角和即可.
【解答】解:∵一个多边形的每个外角都是60°,
∴n=360°÷60°=6,
则内角和为:(6﹣2) 180°=720°,
故答案为:720°.
9.
【分析】设这个多边形的边数为n,根据内角和公式得出(n﹣2)×180°=1440,求出方程的解即可.
【解答】解:设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
10.
【分析】由在平行四边形ABCD中,可得==,即可得=﹣,=﹣,又由=+,即可求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴==,
∵=,
∴=﹣,=﹣,
∴=+=﹣﹣.
故答案为:﹣﹣.
11.
【分析】根据梯形的中位线等于梯形两底和的一半进行计算即可.
【解答】解:设梯形的另一条底边为xcm,
由题意得:6+x=2×5,
解得x=4.
即梯形的另一条底边的长为4cm.
故答案为:4.
12.4.
13.
【分析】过点D作DE∥AC交BC的延长线于点E,作DF⊥BC于F,证平行四边形ADEC,推出AC=DE=BD,∠BDE=90°,根据等腰三角形性质推出BF=DF=EF=BE,求出DF,根据梯形的面积公式求出即可.
【解答】解:过点D作DE∥AC交BC的延长线于点E,
∵AD∥BC(已知),
即AD∥CE,
∴四边形ACED是平行四边形,
∴AD=CE=2,AC=DE,
在等腰梯形ABCD中,AC=DB,
∴DB=DE(等量代换),
∵AC⊥BD,AC∥DE,
∴DB⊥DE,
∴△BDE是等腰直角三角形,
作DF⊥BC于F,
则DF=BE=3,
S梯形ABCD=(AD+BC) DF=(2+4)×3=9.
故答案为:9.
14.
【分析】根据三角形中位线定理求出DE,根据直角三角形的性质求出DF,计算即可.
【解答】解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=3,
∴EF=DE﹣DF=2,
故答案为:2
15.:1.
16.
【分析】根据菱形的对角线互相垂直平分,得已知对角线的一半是5.根据勾股定理,得要求的对角线的一半是12,则另一条对角线的长是24,进而求出菱形的面积.
【解答】解:在菱形ABCD中,AB=13,AC=10,
∵对角线互相垂直平分,
∴∠AOB=90°,AO=5,
在Rt△AOB中,BO==12,
∴BD=2BO=24.
∴则此菱形面积是=120,
故答案为:120.
17.
【分析】用反推法,如果四边形ABCD是平行四边形,会推出什么结论,那么这些结论就是我们要添加的条件.
【解答】解:∵∠ABD=∠CDB,∴AB∥CD,要使四边形ABCD是平行四边形,可添AB=CD,根据一组对边平行且相等的四边形是平行四边形,可使四边形ABCD是平行四边形;或添AD∥BC,根据由两组对边分别平行的四边形是平行四边形,可使四边形ABCD是平行四边形.
三.解答题
18.证明:∵∠D=∠DCE,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.
19.证明:(1)如图,作EM⊥BC于点M,
∵四边形ABCD是矩形,
∴AB⊥BC,
∴EM∥AB,
∴∠ABE=∠BEM,∠BAC=∠CEM,
∵∠ABE+∠CEF=45°,
∴∠BEM+∠CEF=45°,
∵BE⊥EF,
∴∠CEM=45°=∠BAC,
∴∠BAC=∠ACB=45°,
∴AB=BC,
∴矩形ABCD是正方形;
20.(1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AD是边BC上的中线,
∴BD=DC,
∴AE=DC,
又∵AE∥BC,
∴四边形ADCE是平行四边形,
(2)∵∠BAC=90°,AD是边BC上的中线.
∴AD=CD,
∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形,
21.
【解答】解:(1),
,
(2)作图
如图1:=,如图2:=.
22.(1)证明:∵∠ADE=∠BAD,
∴AB∥DE,
∵AE⊥AC,BD⊥AC,
AE∥BD,
∴四边形ABDE是平行四边形;
(2)解:∵DA平分∠BDE,
∴∠AED=∠BDA,
∴∠BAD=∠BDA,
∴BD=AB=5,
设BF=x,则DF=5﹣x,
∴AD2﹣DF2=AB2﹣BF2,
∴62﹣(5﹣x)2=52﹣x2,
∴x=,
∴AF==,
∴AC=2AF=.
23.
【解答】(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形.
24.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS);
(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
∵EG=AE,OA=OC,
∴OE是△ACG的中位线,
∴OE∥CG,
∴EF∥CG,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
由(1)得:△ABE≌△CDF,
∴AE=CF,
∵EG=AE,
∴EG=CF,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
26.(1)证明:∵AD=DE=EB,
∴==,
∵DF∥BC,EG∥AC,
∴==,,
∴,
∴FG∥AB;
(2)解:∵DF∥BC,FG∥AB,
∴,,
∴FG=AB,
∵与同向,
∴=,
∵=,=,
∴=﹣,
∴=.
27.证明:连接FG,FD,GC.
∵EG=ED,EF=EC,
∴四边形FGCD是平行四边形(对角线互相平分的四边形是平行四边形),
∴FG∥DC,FG=DC(平行四边形对边相等且平行),
∵平行四边形ABCD,
∴AB∥DC,AB=DC,
∴AB∥FG,AB=FG,
∴四边形ABGF是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴AF∥BG.
28.解:(1)∵四边形ABCO是矩形,点B的坐标是(﹣6,8).
∴∠BAD=∠OCB=90°,AB=OC=6,OA=BC=8,
∴BO==10;
由折叠的性质得:BE=AB=6,∠BED=∠BAD=90°,DE=AD,
∴OE=BO﹣BE=10﹣6=4,∠OED=90°,
设D(0,a),则OD=a,DE=AD=OA﹣OD=8﹣a,
在Rt△EOD中,由勾股定理得:DE2+OE2=OD2,
即(8﹣a)2+42=a2,解得:a=5,
∴D(0,5);
(2)存在,点M的坐标为(4,0)或(﹣4,0)或(﹣,0)或(﹣,0);理由如下:
①当OM、OE都为菱形的边时,OM=OE=4,
∴M的坐标为(4,0)或(﹣4,0);
②当OM为菱形的边,OE为对角线时,MN垂直平分OE,垂足为G,如图1所示:
则OG=OE=2,
∵OA=8,OD=5,
∴AD=DE=3,
∴E到y轴的距离===,
∴OH=,
∵EM2﹣MH2=42﹣()2,
∴OM2﹣(OM﹣)2=42﹣()2,
解得:OM=,
∴M(﹣,0);
③当OM为菱形的对角线,OE为边时,如图2所示:
同②得:M(﹣,0);
综上所述,在x轴上存在点M,使以M、N、E、O为顶点的四边形是菱形,点M的坐标为(4,0)或(﹣4,0)或(﹣,0)或(﹣,0).
29.解:(1)过D作DH⊥BC,DH与EF、BC分别相交于点G、H,
∵梯形ABCD中,∠B=90°,
∴DH∥AB,
又∵AD∥BC,
∴四边形ABHD是矩形,
∵∠C=45°,
∴∠CDH=45°,
∴CH=DH=AB=8,
∴AD=BH=BC﹣CH=6.
(2)∵DH⊥EF,∠DFE=∠C=∠FDG=45°,
∴FG=DG=AE=x,
∵EG=AD=6,
∴EF=x+6,
∵PE=PF,EF∥BC,
∴∠PFE=∠PEF=∠PMN=∠PNM,
∴PM=PN,
过点P作QR⊥EF,QR与EF、MN分别相交于Q、R,
∵∠MPN=∠EPF=90°,QR⊥MN,
∴PQ=EF=,PR=MN=,
∵QR=BE=8﹣x,
∴,
∴y关于x的函数解析式为y=﹣3x+10.定义域为1≤x<.
(3)当点P在梯形ABCD内部时,由MN=2及(2)的结论得2=﹣3x+10,AE=,
∴(AD+EF) AE=,
当点P在梯形ABCD外部时,由MN=2及与(2)相同的方法得:,AE=x=4,
∴(AD+EF) AE=.
30.解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH==,
∴S△ABE=AE×BH=×4×=;
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=NG=ME=BE,
∴BE=GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD﹣AF=BC﹣EC,即DF=BE,
∴DF=BE=CG.
一.选择题
1.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
2.已知向量、满足||=||,则( )
A.= B.=﹣
C.∥ D.以上都有可能
3.已知点C是线段AB的中点,下列结论中,正确的是( )
A. B. C. D.
4.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
5.下列判断不正确的是( )
A.如果=,那么||=||
B.+=+
C.如果非零向量=k (k≠0),那么与平行或共线
D.+=0
6.如果一个正多边形的每一个外角都是45°,那么这个正多边形的内角和为( )
A.360° B.720° C.1080° D.1440°
7.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
二.填空题
8.如果一个多边形的每个外角都是60°,那么这个多边形内角和的度数为 .
9.一个多边形的内角和为1440°,则这个多边形是 边形.
10.已知:在平行四边形ABCD中,设=,=,那么= (用向量、的式子表示).
11.已知一个梯形的中位线长为5cm,其中一条底边的长为6cm,那么该梯形的另一条底边的长是 cm.
12.菱形ABCD中,已知AB=4,∠B=60°,那么BD的长是 .
13.如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=2,BC=4,则该梯形的面积为 .
14.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为 .
15.如图,梯形ABCD中,AD∥BC,∠A=90°,它恰好能按图示方式被分割成四个全等的直角梯形,则AB:BC= .
16.如果菱形边长为13,一条对角线长为10,那么它的面积为 .
17.在四边形ABCD中,BD是对角线,∠ABD=∠CDB,要使四边形ABCD是平行四边形只须添加一个条件,这个条件可以是 (只需写出一种情况).
三.解答题
18.已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.
19.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.
求证:四边形ABCD是正方形;
20.如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
21.如图,已知△ABC中,点D为边AC的中点,设,,
(1)试用向量,表示下列向量:= ;= ;
(2)求作:、.
(保留作图痕迹,不要求写作法,写出结果).
22.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
23.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
24.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当线段AB与线段AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
25.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
26.如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,EG∥AC.
(1)求证:FG∥AB;
(2)设=,=,请用向量、表示.
27.已知:如图,点E、G在平行四边形ABCD的边AD上,EG=ED,延长CE到点F,使得EF=EC.求证:AF∥BG.
28.如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(﹣6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
(1)求点D的坐标;
(2)若点N是平面内任一点,在x轴上是否存在点M,使M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
29.在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AB=8,BC=14,点E、F分别在边AB、CD上,EF∥AD,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
(1)求边AD的长;
(2)如图,当点P在梯形ABCD内部时,求y关于x的函数解析式,并写出定义域;
(3)如果MN的长为2,求梯形AEFD的面积.
30.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
答案
一.选择题
1.
【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.
【解答】解:如图所示:∵AB∥CD,
∴∠B+∠C=180°,
当∠A=∠C时,则∠A+∠B=180°,
故AD∥BC,
则四边形ABCD是平行四边形.
故选:C.
2.
【分析】利用单位向量的定义和性质直接判断即可.
【解答】解:若向量、满足||=||,
可得:=,或=﹣,或∥,
故选:D.
3.
【分析】根据题意画出图形,因为点C是线段AB的中点,所以根据线段中点的定义解答.
【解答】解:A、=,故本选项错误;
B、=,故本选项正确;
C、+=,故本选项错误;
D、+=,故本选项错误.
故选:B.
4.
【分析】根据多边形的内角和公式(n﹣2) 180°和外角和定理列出方程,然后求解即可.
【解答】解:设多边形的边数为n,
由题意得,(n﹣2) 180°=2×360°,
解得n=6,
所以,这个多边形是六边形.
故选:D.
5.
【分析】根据模的定义,可确定A正确;根据平面向量的交换律,可判定B正确,又由如果非零向量非零向量=k (k≠0),那么∥,可得C正确;利用相反向量的知识,可判定D错误.
【解答】解:A、如果=,那么||=||,故此选项正确;
B、+=+,故本选项正确;
C、如果非零向量=k (k≠0),那么与平行或共线,故此选项正确;
D、+=,故此选项错误;
故选:D.
6.
【分析】多边形的外角和是360度,即可得到外角的个数,即多边形的边数.根据多边形的内角和定理即可求解.
【解答】解:多边形的边数是:360÷45=8.
则内角和是:(8﹣2)×180°=1080°.
故选:C.
7.
【分析】由平行四边形的判定与性质、矩形的判定分别对各个选项进行判断即可.
【解答】解:A、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵AD∥BC,
∴∠A+∠B=∠C+∠D=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,AB=CD,故选项C符合题意;
D、∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴AB⊥AD,AB⊥BC,AB的长为AD、BC间的距离,
又∵AB=CD,
∴CD⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形,故选项D不符合题意;
故选:C.
二.填空题
8.
【分析】根据正多边形的性质,边数等于360°除以每一个外角的度数,然后利用多边形的内角和公式计算内角和即可.
【解答】解:∵一个多边形的每个外角都是60°,
∴n=360°÷60°=6,
则内角和为:(6﹣2) 180°=720°,
故答案为:720°.
9.
【分析】设这个多边形的边数为n,根据内角和公式得出(n﹣2)×180°=1440,求出方程的解即可.
【解答】解:设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
10.
【分析】由在平行四边形ABCD中,可得==,即可得=﹣,=﹣,又由=+,即可求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴==,
∵=,
∴=﹣,=﹣,
∴=+=﹣﹣.
故答案为:﹣﹣.
11.
【分析】根据梯形的中位线等于梯形两底和的一半进行计算即可.
【解答】解:设梯形的另一条底边为xcm,
由题意得:6+x=2×5,
解得x=4.
即梯形的另一条底边的长为4cm.
故答案为:4.
12.4.
13.
【分析】过点D作DE∥AC交BC的延长线于点E,作DF⊥BC于F,证平行四边形ADEC,推出AC=DE=BD,∠BDE=90°,根据等腰三角形性质推出BF=DF=EF=BE,求出DF,根据梯形的面积公式求出即可.
【解答】解:过点D作DE∥AC交BC的延长线于点E,
∵AD∥BC(已知),
即AD∥CE,
∴四边形ACED是平行四边形,
∴AD=CE=2,AC=DE,
在等腰梯形ABCD中,AC=DB,
∴DB=DE(等量代换),
∵AC⊥BD,AC∥DE,
∴DB⊥DE,
∴△BDE是等腰直角三角形,
作DF⊥BC于F,
则DF=BE=3,
S梯形ABCD=(AD+BC) DF=(2+4)×3=9.
故答案为:9.
14.
【分析】根据三角形中位线定理求出DE,根据直角三角形的性质求出DF,计算即可.
【解答】解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=3,
∴EF=DE﹣DF=2,
故答案为:2
15.:1.
16.
【分析】根据菱形的对角线互相垂直平分,得已知对角线的一半是5.根据勾股定理,得要求的对角线的一半是12,则另一条对角线的长是24,进而求出菱形的面积.
【解答】解:在菱形ABCD中,AB=13,AC=10,
∵对角线互相垂直平分,
∴∠AOB=90°,AO=5,
在Rt△AOB中,BO==12,
∴BD=2BO=24.
∴则此菱形面积是=120,
故答案为:120.
17.
【分析】用反推法,如果四边形ABCD是平行四边形,会推出什么结论,那么这些结论就是我们要添加的条件.
【解答】解:∵∠ABD=∠CDB,∴AB∥CD,要使四边形ABCD是平行四边形,可添AB=CD,根据一组对边平行且相等的四边形是平行四边形,可使四边形ABCD是平行四边形;或添AD∥BC,根据由两组对边分别平行的四边形是平行四边形,可使四边形ABCD是平行四边形.
三.解答题
18.证明:∵∠D=∠DCE,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.
19.证明:(1)如图,作EM⊥BC于点M,
∵四边形ABCD是矩形,
∴AB⊥BC,
∴EM∥AB,
∴∠ABE=∠BEM,∠BAC=∠CEM,
∵∠ABE+∠CEF=45°,
∴∠BEM+∠CEF=45°,
∵BE⊥EF,
∴∠CEM=45°=∠BAC,
∴∠BAC=∠ACB=45°,
∴AB=BC,
∴矩形ABCD是正方形;
20.(1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AD是边BC上的中线,
∴BD=DC,
∴AE=DC,
又∵AE∥BC,
∴四边形ADCE是平行四边形,
(2)∵∠BAC=90°,AD是边BC上的中线.
∴AD=CD,
∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形,
21.
【解答】解:(1),
,
(2)作图
如图1:=,如图2:=.
22.(1)证明:∵∠ADE=∠BAD,
∴AB∥DE,
∵AE⊥AC,BD⊥AC,
AE∥BD,
∴四边形ABDE是平行四边形;
(2)解:∵DA平分∠BDE,
∴∠AED=∠BDA,
∴∠BAD=∠BDA,
∴BD=AB=5,
设BF=x,则DF=5﹣x,
∴AD2﹣DF2=AB2﹣BF2,
∴62﹣(5﹣x)2=52﹣x2,
∴x=,
∴AF==,
∴AC=2AF=.
23.
【解答】(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形.
24.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS);
(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
∵EG=AE,OA=OC,
∴OE是△ACG的中位线,
∴OE∥CG,
∴EF∥CG,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
由(1)得:△ABE≌△CDF,
∴AE=CF,
∵EG=AE,
∴EG=CF,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
26.(1)证明:∵AD=DE=EB,
∴==,
∵DF∥BC,EG∥AC,
∴==,,
∴,
∴FG∥AB;
(2)解:∵DF∥BC,FG∥AB,
∴,,
∴FG=AB,
∵与同向,
∴=,
∵=,=,
∴=﹣,
∴=.
27.证明:连接FG,FD,GC.
∵EG=ED,EF=EC,
∴四边形FGCD是平行四边形(对角线互相平分的四边形是平行四边形),
∴FG∥DC,FG=DC(平行四边形对边相等且平行),
∵平行四边形ABCD,
∴AB∥DC,AB=DC,
∴AB∥FG,AB=FG,
∴四边形ABGF是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴AF∥BG.
28.解:(1)∵四边形ABCO是矩形,点B的坐标是(﹣6,8).
∴∠BAD=∠OCB=90°,AB=OC=6,OA=BC=8,
∴BO==10;
由折叠的性质得:BE=AB=6,∠BED=∠BAD=90°,DE=AD,
∴OE=BO﹣BE=10﹣6=4,∠OED=90°,
设D(0,a),则OD=a,DE=AD=OA﹣OD=8﹣a,
在Rt△EOD中,由勾股定理得:DE2+OE2=OD2,
即(8﹣a)2+42=a2,解得:a=5,
∴D(0,5);
(2)存在,点M的坐标为(4,0)或(﹣4,0)或(﹣,0)或(﹣,0);理由如下:
①当OM、OE都为菱形的边时,OM=OE=4,
∴M的坐标为(4,0)或(﹣4,0);
②当OM为菱形的边,OE为对角线时,MN垂直平分OE,垂足为G,如图1所示:
则OG=OE=2,
∵OA=8,OD=5,
∴AD=DE=3,
∴E到y轴的距离===,
∴OH=,
∵EM2﹣MH2=42﹣()2,
∴OM2﹣(OM﹣)2=42﹣()2,
解得:OM=,
∴M(﹣,0);
③当OM为菱形的对角线,OE为边时,如图2所示:
同②得:M(﹣,0);
综上所述,在x轴上存在点M,使以M、N、E、O为顶点的四边形是菱形,点M的坐标为(4,0)或(﹣4,0)或(﹣,0)或(﹣,0).
29.解:(1)过D作DH⊥BC,DH与EF、BC分别相交于点G、H,
∵梯形ABCD中,∠B=90°,
∴DH∥AB,
又∵AD∥BC,
∴四边形ABHD是矩形,
∵∠C=45°,
∴∠CDH=45°,
∴CH=DH=AB=8,
∴AD=BH=BC﹣CH=6.
(2)∵DH⊥EF,∠DFE=∠C=∠FDG=45°,
∴FG=DG=AE=x,
∵EG=AD=6,
∴EF=x+6,
∵PE=PF,EF∥BC,
∴∠PFE=∠PEF=∠PMN=∠PNM,
∴PM=PN,
过点P作QR⊥EF,QR与EF、MN分别相交于Q、R,
∵∠MPN=∠EPF=90°,QR⊥MN,
∴PQ=EF=,PR=MN=,
∵QR=BE=8﹣x,
∴,
∴y关于x的函数解析式为y=﹣3x+10.定义域为1≤x<.
(3)当点P在梯形ABCD内部时,由MN=2及(2)的结论得2=﹣3x+10,AE=,
∴(AD+EF) AE=,
当点P在梯形ABCD外部时,由MN=2及与(2)相同的方法得:,AE=x=4,
∴(AD+EF) AE=.
30.解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH==,
∴S△ABE=AE×BH=×4×=;
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=NG=ME=BE,
∴BE=GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD﹣AF=BC﹣EC,即DF=BE,
∴DF=BE=CG.
