沪教版九年级数学下册试题 期中测试卷(含解析)
文档属性
| 名称 | 沪教版九年级数学下册试题 期中测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览


文档简介
期中测试卷
一、选择题:本题共10个小题,每小题3分,共30分。
1.已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O有公共点( ).
A.0个 B.1个 C.2个 D.无法确定
2.若⊙P的半径为5,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
3.用一个圆心角为,半径为12的扇形作为一个圆锥的侧面,则该圆锥底面半径为( )
A. B.4 C.6 D.8
4.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
5.如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
A.50° B.55° C.65° D.75°
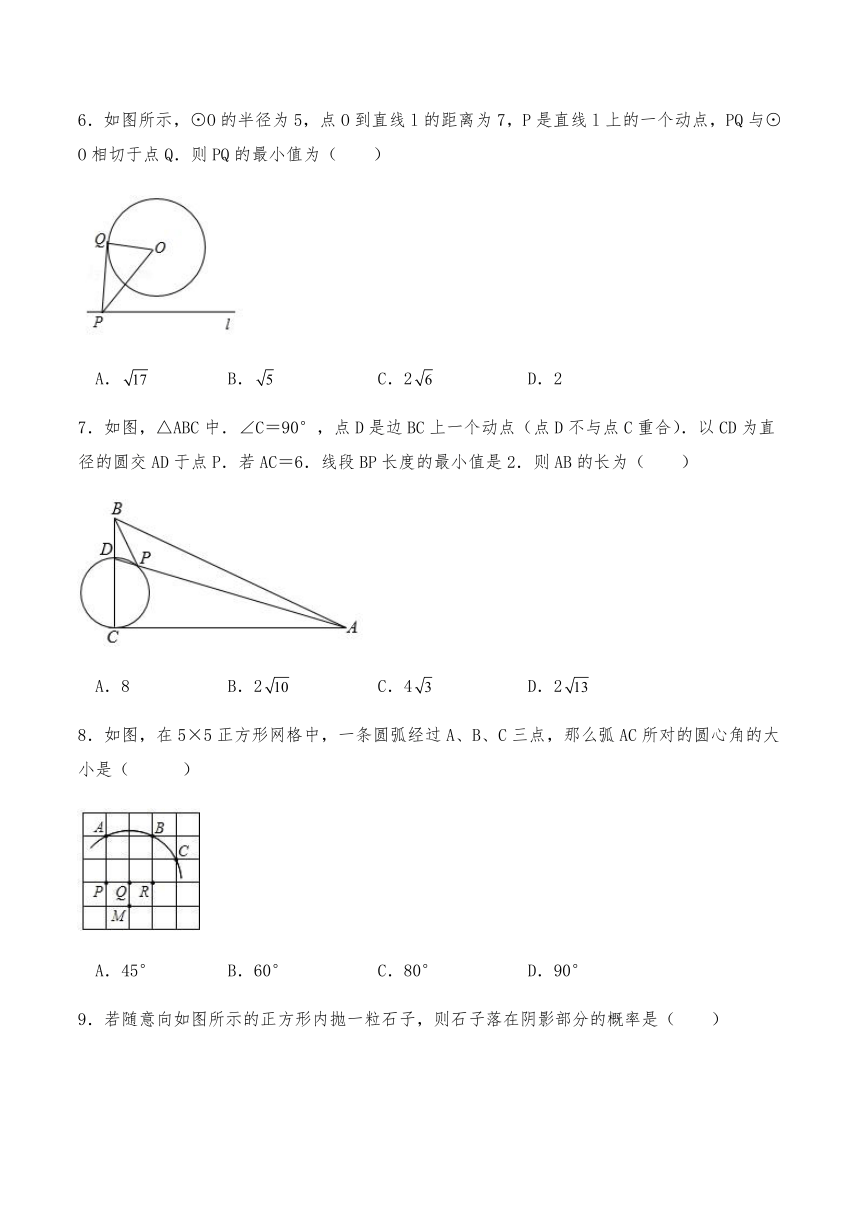
6.如图所示,⊙O的半径为5,点O到直线l的距离为7,P是直线l上的一个动点,PQ与⊙O相切于点Q.则PQ的最小值为( )
A. B. C.2 D.2
7.如图,△ABC中.∠C=90°,点D是边BC上一个动点(点D不与点C重合).以CD为直径的圆交AD于点P.若AC=6.线段BP长度的最小值是2.则AB的长为( )
A.8 B.2 C.4 D.2
8.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么弧AC所对的圆心角的大小是( )
A.45° B.60° C.80° D.90°
9.若随意向如图所示的正方形内抛一粒石子,则石子落在阴影部分的概率是( )
A.1 B.1 C. D.1
10.矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A.3.6 B. C.3.5 D.
二、填空题:本题共8个小题,每题3分,共24分。
11.已知:⊙O的半径OA=4,点A、B、C为圆上不重合的三个点,弦AB的长为4,则∠ACB=_____.
12.已知正五边形的外接圆直径为6,那么该正五边形外接圆的半径为_____.
13.Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,则以2.6cm为半径的⊙C与直线AB的位置关系是__________.
14.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD= ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为_____________.(结果保留π和根号)
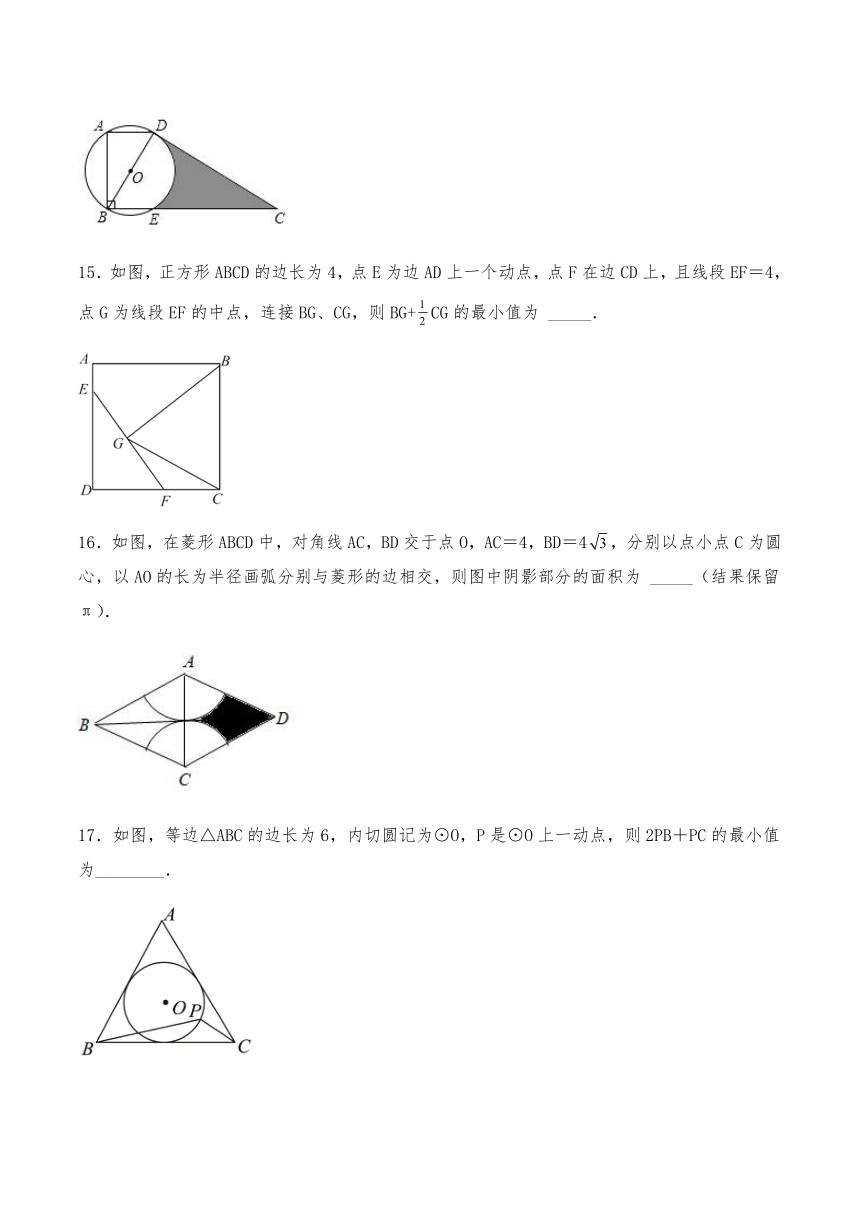
15.如图,正方形ABCD的边长为4,点E为边AD上一个动点,点F在边CD上,且线段EF=4,点G为线段EF的中点,连接BG、CG,则BG+CG的最小值为 _____.
16.如图,在菱形ABCD中,对角线AC,BD交于点O,AC=4,BD=4,分别以点小点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 _____(结果保留π).
17.如图,等边△ABC的边长为6,内切圆记为⊙O,P是⊙O上一动点,则2PB+PC的最小值为________.
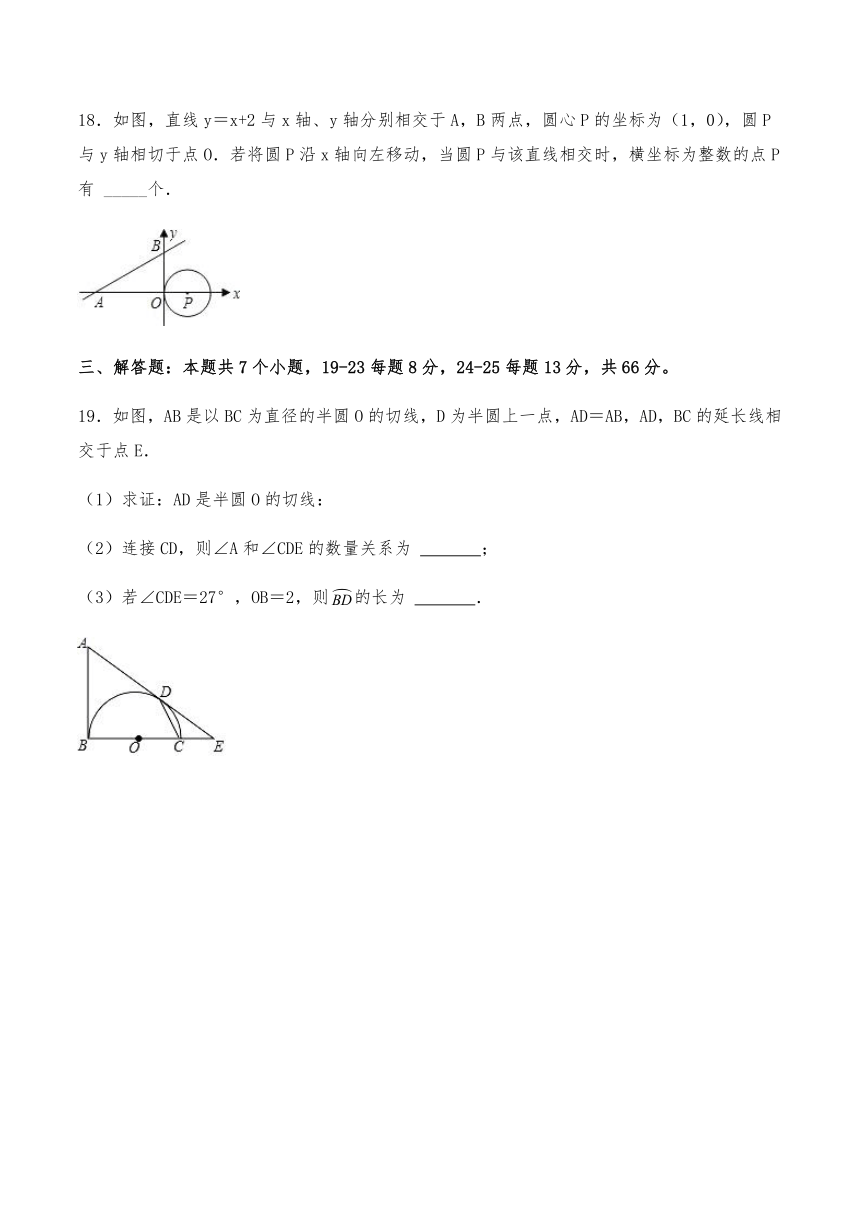
18.如图,直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P有 _____个.
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线:
(2)连接CD,则∠A和∠CDE的数量关系为 ;
(3)若∠CDE=27°,OB=2,则的长为 .
20.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠E=∠D;
(2)若AB=5,BC-AC=1,求CE的长.
21.如图,内接于,弦AE与弦BC交于点D,连接BO,,
(1)求证:;
(2)若,求的度数;
(3)在(2)的条件下,过点O作于点H,延长HO交AB于点P,若,,求半径的长.
22.如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.
(1)求证:BE = CE.
(2)以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积
(3)若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
23.如图,是的直径,为上一点(不与点,重合)连接,,过点作,垂足为点.将沿翻折,点落在点处得,交于点.
(1)求证:是的切线;
(2)若,,求阴影部分面积.
24.如图所示,是的直径,点、是上不同的两点,直线交线段于点,交过点的直线于点,若,且.
(1)求证:直线是的切线;
(2)连接、、、,若.
①求证:;
②过点作,交线段于点,点为线段的中点,若,求线段的长度.
答案
一、选择题
1.C
【分析】根据⊙O半径为5,点O到直线l的距离为3得到直线l与⊙O相交,即可判断出直线l与⊙O有两个公共点.
【详解】解:∵⊙O半径为5,点O到直线l的距离为3,
∴d<r,
∴直线l与⊙O相交,
∴直线l与⊙O有两个公共点.
故选:C
2.B
【分析】由勾股定理等性质算出点与圆心的距离,则时,点在圆外;当时,点在圆上;当时,点在圆内.
【详解】解:由勾股定理,得
,
,
原点在上.
故选:B.
3.B
【分析】根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
【详解】解:设圆锥底面的半径为,
扇形的弧长为:,
圆锥的底面周长等于它的侧面展开图的弧长,
根据题意得,
解得:.
故选:B.
4.C
【分析】根据题意连接OC,依据切线性质得出,进而利用勾股定理即可求出PC.
【详解】解:连接OC,
∵PC为⊙O的切线,
∴,
∵OB=OC=3,PB=2,
∴,
∴.
故选:C.
5.C
【分析】首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
6.C
【分析】由切线的性质可知OQ⊥PQ,在Rt△OPQ中,OQ=5,则可知当OP最小时,PQ有最小值,当OP⊥l时,OP最小,利用勾股定理可求得PQ的最小值.
【详解】解:∵PQ与⊙O相切于点Q,
∴OQ⊥PQ,
∴PQ2=OP2-OQ2=OP2-52=OP2-25,
∴当OP最小时,PQ有最小值,
∵点O到直线l的距离为7,
∴OP的最小值为7,
∴PQ的最小值=,
故选:C.
7.D
【分析】利用圆周角定理得到∠CPD=90°,则可判断点P在以AC为直径的⊙O上,如图,连接OB交⊙O于P′,利用点与圆的位置关系得到BP′=2,再利用勾股定理计算出BC,然后在Rt△ABC中利用勾股定理可计算出AB.
【详解】解:∵CD为直径,
∴∠CPD=90°,
∵∠APC=90°,
∴点P在以AC为直径的⊙O上,如图,
连接OB交⊙O于P′,
∵线段BP长度的最小值是2,
∴BP′=2,
∴OB=2+3=5,
在Rt△OBC中,BC=,
在Rt△ABC中,AB=.
故选:D.
8.D
【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,分别作AB,BC的垂直平分线即可得到圆心,进而解答即可.
【详解】解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即弧AC所对的圆心角是90°,
故选:D.
9.A
【分析】设正方形ABCD的边长为a,然后根据石子落在阴影部分的概率即为阴影部分面积与正方形面积的比,由此进行求解即可.
【详解】解:如图所示,设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴∠C=90°,
∴
,
∴,
∴石子落在阴影部分的概率是,
故选A.
10.A
【分析】连接ON、OG、OF,作OH⊥CD于H,在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,可得FN的值,设FG=x,由OG2=ON2-GN2=OF2-FG2,可得FG的值,进而即可求解.
【详解】解:连接ON、OG、OF,作OH⊥CD于H,
∵点O是矩形对称中心,矩形沿MN折叠,使点C恰好落在AD边的中点F处,
∴DH=HC=CD=6,OF=AB=6,
∵以O为圆心的圆与NF相切,
∴OG⊥NF,
由折叠的性质可知,NC=NF,
在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,
解得,FN=,
∴DN=12-=,
∴HN=HD-DN=6-=,
设FG=x,则NG=-x,
∵OG2=ON2-GN2=OF2-FG2,
即42+()2-(-x)2=62-x2,
解得,x=4.8,
∴OG=
故选:A.
二、填空题:。
11.45°或135°135°或45°
【分析】根据题意画出图形,先判断出∠AOB=90°,再分两种情况用同弧所对的圆心角和圆周角的关系确定和圆的内接四边形的性质即可.
【详解】解:如图,
∵OA=OB=4,AB=4,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
当点C在优弧上时,∠ACB=∠AOB=45°,
点C在劣弧上时,∠AC'B+∠ACB=180°,
∴∠AC'B=180°﹣45°=135°,
∴∠ACB=45°或135°,
故答案为45°或135°.
12.3
【分析】根据半径是直径的一半直接写出答案即可.
【详解】解:∵正五边形的外接圆直径为6,
∴该正五边形外接圆的半径为6÷2=3,
故答案为:3.
13.相交
【分析】由勾股定理可求AB的长度,根据三角形的面积公式可求点C到直线AB的距离,即可判断⊙C与直线AB的位置关系.
【详解】解:∵∠C=90°,AC=4,BC=3,
∴AB==5,
设点C到直线AB的距离为d,
∵S△ABC=AB×d=×AC×BC
∴5d=12
∴d=
∵d<r=2.6
∴⊙C与直线AB的位置关系为相交,
故答案为:相交.
14.
【分析】连接OE,根据∠ABC=90°,AD=,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积-△ABD的面积-△OBE的面积-扇形ODE的面积.
【详解】解:连接OE,过点O作OF⊥BE于点F,
∵∠ABC=90°,AD=,∠ABD=30°,
∴BD=2AD=2,∠ADB=60°,
∴,,
∵AD∥BC,
∴∠DBC=∠ADB=60°,
∵OB=OE,∠DBC=60°,
∴△OBE是等边三角形,
∴BE=OB=,∠BOE=60°,
∴∠DOE=120°,
∵OF⊥BE,
∴,
∴,
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC==2BD=4,
,
故答案为:.
15.5
【分析】因为DG=EF=2,所以G在以D为圆心,2为半径圆上运动,取DI=1,可证△GDI∽△CDG,从而得出GI=CG,然后根据三角形三边关系,得出BI是其最小值
【详解】解:如图,
在Rt△DEF中,G是EF的中点,
∴DG=,
∴点G在以D为圆心,2为半径的圆上运动,
在CD上截取DI=1,连接GI,
∴==,
∴∠GDI=∠CDG,
∴△GDI∽△CDG,
∴=,
∴IG=,
∴BG+=BG+IG≥BI,
∴当B、G、I共线时,BG+CG最小=BI,
在Rt△BCI中,CI=3,BC=4,
∴BI=5,
故答案是:5.
16.
【分析】根据菱形的性质得到AC⊥BD,根据直角三角形的性质求出∠ABO=30°,根据扇形面积公式、三角形面积公式计算即可.
【详解】解:∵四边形ABCD是菱形,AC=4,BD=4,
∴AC⊥BD,AO=2,BO=2,
AB=,
∴AB=2AO,
∴∠ABO=30°,∠BAO=∠DAO=60°,
∴阴影部分的面积=×2×4-=4,
故答案为:.
17.
【分析】如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,,首先证明,得到,所以,而(当且仅当、P、共线时取等号),从而计算出得到的最小值.
【详解】解:如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,BO,
为的内切圆,
,
是等边三角形,
,,
,
同理可得
在中,,
∴,
∴,
,
,,,
,
,
,
,
,
的最小值为的长度,
的最小值为的长度,
,,
,
的最小值为.
故答案为:.
18.3
【分析】根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
【详解】解:∵直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),
∴A点的坐标为:(﹣2,0),B点的坐标为:(0,2),
∴AB=2,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
∵∠AC1P1=∠AOB=90°,∠C1AP1=∠OAB,
∴△AP1C1∽△ABO,
∴=,即
∴AP1=,
∴P1的坐标为:(﹣2+,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
同理△AP2C2∽△ABO,
∴=,
∴AP2=,
P2的坐标为:(﹣2﹣,0),
从﹣2﹣到﹣2+,整数点有﹣1,﹣2,﹣3,故横坐标为整数的点P的个数是,3个.
故答案为:3.
三、解答题。
19.
(1)证明:连接OD,BD,如图,
∵AB是⊙O的切线,
∴AB⊥BC,
∴∠ABO=90°,
∵AB=AD,
∴∠ABD=∠ADB,
∵OB=OD,
∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,即∠ADO=90°,
∴AD⊥OD,
又∵OD是圆O的半径,
∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD,
∴∠DOC=∠A,
∵AD是半圆O的切线,
∴OD⊥AE,
∴∠ODE=90°,
∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,
∴∠DOC=2∠BDO,
∴∠DOC=2∠CDE,
∴∠A=2∠CDE,
故答案为:∠A=2∠CDE;
(3)解:∵∠CDE=27°,
∴∠DOC=2∠CDE=54°,
∴,
∴的长=.
故答案为:π.
20.
(1)∵AB为直径,故∠ACB=90°,CD=BC,AC=AC
∴(SAS)
∴∠D=∠B
又∵∠E=∠B
∴∠E=∠D
(2)由(1)可知为直角三角形,故有
即
解得AC=3,BC=4
则DC=4
又∵∠E=∠D,
故CD=CE=4
21.解:(1)如图所示,连接OA,
∴,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠OAB+∠OBA+∠AOB=180°,
∴,即∠OBA+∠ACB=90°,
又∵∠OBA=∠CAE,
∴∠ACB+∠CAE=90°,
∴∠ADC=90°,
∴AE⊥BC;
(2)如图所示,连接CE,
∴∠ABC=∠AEC,
∵,AE⊥BC,
∴,
∴∠AEC=30°,
∴∠ABC=30°;
(3)如图所示,过点O作OF⊥AB于F,
∴BF=AF,
设FP=x,
∴BF=AF=AP+PF=6+x,
∴BP=BF+PF=6+2x
∵∠ABC=30°,PH⊥BC,
∴∠BPH=60°,BP=2PH,
又∵∠OF⊥AB,
∴∠OFP=90°,
∴∠POF=30°,
∴OP=2FP=2x,
∴PH=OP+OH=1+2x,
∴BP=2+4x,
∴2+4x=6+2x,
解得x=2,
∴PF=2,BF=8,PO=4,
∴,
∴,
∴圆O的半径长为.
22.
(1)证明:由题意可知:,为等边三角形,
点是BC的中点,
是等边的中线,且,
,
,
.
(2)解:如图所示:
与BC相切,且,
点是切点,并且是该扇形的半径,
,且,
,
,
在中,,
,
是BC的中点,
在中,由勾股定理可知:,解得,
扇形FEG的面积为.
(3)解:设圆锥底面圆半径为,
扇形FEG的弧长为: ,
扇形FEG的弧长等于其围成的圆锥的底面圆的周长,
,解得 ,
故圆锥的底面圆的半径为.
23.解:(1)如图,连接OC,
∵,
∴∠CDA=90°,
∵翻折得到,
∴∠EAC=∠DAC,∠E=∠CDA=90°,
∴∠EAD=2∠DAC,
∵OA=OC,
∴∠OAC=∠OCA
∴∠COD=2∠OAC,
∴∠COD=∠EAD,
∴OCAE,
∴∠ECO=180°-∠E=90°,
∴OC⊥EC,
∴是的切线;
(2)如图,连接,过点作于点,
∵∠E=∠ECO=90°,
∴四边形OCEG为矩形.
∵,,
∴,
∴,
∴,
∵于点,OA=OF=2,
∴,∠FAO=∠AFO=30°,
∵OCAE,
∴∠COF=∠AFO=30°,
∴矩形OCEG面积为,
△OGF面积为,
扇形COF面积为
∴阴影部分面积=矩形OCEG面积-△OGF面积-扇形COF面积=.
24.解:(1)证:因为,且,
∴,
∴,
∴,
∴直线是的切线;
(2)①∵,
又∵,
∴,
∵,
∴.;
②∵,
∴,
设圆的半径为r,
∵, ,
∴,
∴;
∵点为线段的中点,
∴,
∵,
∴,
∴,
∴,
∴线段的长度为1.
【高效培优】2021—2022学年沪教版九年级数学下册轻松冲刺学神考霸必刷卷
【期中满分押题】夯实基础过关卷
(考试范围:第二十七章 考试时间:120分钟 试卷满分:120分)
学校:___________姓名:___________班级:___________考号:___________
本卷试题共三大题,共25小题,单选10题,填空8题,解答7题,限时120分钟,满分120分,本卷题型精选核心常考重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!
选择题:本题共10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2021·全国·中考真题)已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O有公共点( ).
A.0个 B.1个 C.2个 D.无法确定
【答案】C
【分析】根据⊙O半径为5,点O到直线l的距离为3得到直线l与⊙O相交,即可判断出直线l与⊙O有两个公共点.
【详解】解:∵⊙O半径为5,点O到直线l的距离为3,
∴d<r,
∴直线l与⊙O相交,
∴直线l与⊙O有两个公共点.
故选:C
【点睛】本题考查了直线与圆的位置关系,能根据圆心到直线的距离d与圆的半径r关系判断位置关系是解题关键.当d>r时,直线与圆相离,没有公共点,当d=r时,直线与圆相切,有一个公共点,当d<r时,直线与圆相交,有两个公共点.
2.(2021·上海·九年级期末)若⊙P的半径为5,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
【答案】B
【分析】由勾股定理等性质算出点与圆心的距离,则时,点在圆外;当时,点在圆上;当时,点在圆内.
【详解】解:由勾股定理,得
,
,
原点在上.
故选:B.
【点睛】本题考查了点与圆的位置关系,解题的关键是要记住若半径为,点到圆心的距离为,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.
3.(2021·天津·九年级期末)用一个圆心角为,半径为12的扇形作为一个圆锥的侧面,则该圆锥底面半径为( )
A. B.4 C.6 D.8
【答案】B
【分析】根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
【详解】解:设圆锥底面的半径为,
扇形的弧长为:,
圆锥的底面周长等于它的侧面展开图的弧长,
根据题意得,
解得:.
故选:B.
【点睛】本题考查的是圆锥的计算,解题的关键是掌握弧长公式、周长公式和圆锥与扇形的对应关系.
4.(2021·山东·日照港中学)如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
【答案】C
【分析】根据题意连接OC,依据切线性质得出,进而利用勾股定理即可求出PC.
【详解】解:连接OC,
∵PC为⊙O的切线,
∴,
∵OB=OC=3,PB=2,
∴,
∴.
故选:C.
【点睛】本题考查切线的性质,熟练掌握切线的性质以及勾股定理的运用是解题的关键.
5.(2021·安徽淮南·)如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
A.50° B.55° C.65° D.75°
【答案】C
【分析】首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
6.(2021·浙江·绍兴市博雅学校)如图所示,⊙O的半径为5,点O到直线l的距离为7,P是直线l上的一个动点,PQ与⊙O相切于点Q.则PQ的最小值为( )
A. B. C.2 D.2
【答案】C
【分析】由切线的性质可知OQ⊥PQ,在Rt△OPQ中,OQ=5,则可知当OP最小时,PQ有最小值,当OP⊥l时,OP最小,利用勾股定理可求得PQ的最小值.
【详解】解:∵PQ与⊙O相切于点Q,
∴OQ⊥PQ,
∴PQ2=OP2-OQ2=OP2-52=OP2-25,
∴当OP最小时,PQ有最小值,
∵点O到直线l的距离为7,
∴OP的最小值为7,
∴PQ的最小值=,
故选:C.
【点睛】本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键.
7.(2021·浙江·杭州市公益中学)如图,△ABC中.∠C=90°,点D是边BC上一个动点(点D不与点C重合).以CD为直径的圆交AD于点P.若AC=6.线段BP长度的最小值是2.则AB的长为( )
A.8 B.2 C.4 D.2
【答案】D
【分析】利用圆周角定理得到∠CPD=90°,则可判断点P在以AC为直径的⊙O上,如图,连接OB交⊙O于P′,利用点与圆的位置关系得到BP′=2,再利用勾股定理计算出BC,然后在Rt△ABC中利用勾股定理可计算出AB.
【详解】解:∵CD为直径,
∴∠CPD=90°,
∵∠APC=90°,
∴点P在以AC为直径的⊙O上,如图,
连接OB交⊙O于P′,
∵线段BP长度的最小值是2,
∴BP′=2,
∴OB=2+3=5,
在Rt△OBC中,BC=,
在Rt△ABC中,AB=.
故选:D.
【点睛】本题主要考查了圆周角定理,点与圆的位置关系,勾股定理,准确计算是解题的关键.
8.(2022·黑龙江·大庆市第三十六中学)如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么弧AC所对的圆心角的大小是( )
A.45° B.60° C.80° D.90°
【答案】D
【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,分别作AB,BC的垂直平分线即可得到圆心,进而解答即可.
【详解】解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即弧AC所对的圆心角是90°,
故选:D.
【点睛】本题考查了垂径定理的推论:弦的垂直平分线必过圆心.这也是常用来确定圆心的方法.
9.(2021·贵州黔西·)若随意向如图所示的正方形内抛一粒石子,则石子落在阴影部分的概率是( )
A.1 B.1 C. D.1
【答案】A
【分析】设正方形ABCD的边长为a,然后根据石子落在阴影部分的概率即为阴影部分面积与正方形面积的比,由此进行求解即可.
【详解】解:如图所示,设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴∠C=90°,
∴
,
∴,
∴石子落在阴影部分的概率是,
故选A.
【点睛】本题主要考查了几何概率,正方形的性质,扇形面积公式,解题的关键在于能够根据题意得到石子落在阴影部分的概率即为阴影部分面积与正方形面积的比.
10.(2021·湖北·武汉七一华源中学)矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A.3.6 B. C.3.5 D.
【答案】A
【分析】连接ON、OG、OF,作OH⊥CD于H,在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,可得FN的值,设FG=x,由OG2=ON2-GN2=OF2-FG2,可得FG的值,进而即可求解.
【详解】解:连接ON、OG、OF,作OH⊥CD于H,
∵点O是矩形对称中心,矩形沿MN折叠,使点C恰好落在AD边的中点F处,
∴DH=HC=CD=6,OF=AB=6,
∵以O为圆心的圆与NF相切,
∴OG⊥NF,
由折叠的性质可知,NC=NF,
在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,
解得,FN=,
∴DN=12-=,
∴HN=HD-DN=6-=,
设FG=x,则NG=-x,
∵OG2=ON2-GN2=OF2-FG2,
即42+()2-(-x)2=62-x2,
解得,x=4.8,
∴OG=
故选:A.
【点睛】本题主要考查圆的切线的性质,矩形的性质,折叠的性质,勾股定理,添加辅助线,构造直角三角形是解题的关键.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·北京·人大附中)已知:⊙O的半径OA=4,点A、B、C为圆上不重合的三个点,弦AB的长为4,则∠ACB=_____.
【答案】45°或135°135°或45°
【分析】根据题意画出图形,先判断出∠AOB=90°,再分两种情况用同弧所对的圆心角和圆周角的关系确定和圆的内接四边形的性质即可.
【详解】解:如图,
∵OA=OB=4,AB=4,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
当点C在优弧上时,∠ACB=∠AOB=45°,
点C在劣弧上时,∠AC'B+∠ACB=180°,
∴∠AC'B=180°﹣45°=135°,
∴∠ACB=45°或135°,
故答案为45°或135°.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
12.(2021·陕西咸阳·)已知正五边形的外接圆直径为6,那么该正五边形外接圆的半径为_____.
【答案】3
【分析】根据半径是直径的一半直接写出答案即可.
【详解】解:∵正五边形的外接圆直径为6,
∴该正五边形外接圆的半径为6÷2=3,
故答案为:3.
【点睛】本题考查了正多边形和圆的知识,知道等圆或同圆中直径是半径的2倍是解答本题的关键.
13.(2021·重庆江津·)Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,则以2.6cm为半径的⊙C与直线AB的位置关系是__________.
【答案】相交
【分析】由勾股定理可求AB的长度,根据三角形的面积公式可求点C到直线AB的距离,即可判断⊙C与直线AB的位置关系.
【详解】解:∵∠C=90°,AC=4,BC=3,
∴AB==5,
设点C到直线AB的距离为d,
∵S△ABC=AB×d=×AC×BC
∴5d=12
∴d=
∵d<r=2.6
∴⊙C与直线AB的位置关系为相交,
故答案为:相交.
【点睛】本题考查直线与圆的位置关系,勾股定理,三角形的面积公式,若设⊙O的半径为r,圆心O到直线l的距离为d,则①直线l和⊙O相交 d<r,②直线l和⊙O相切 d=r,③直线l和⊙O相离 d>r.
14.(2021·甘肃·金昌市第五中学)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD= ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为_____________.(结果保留π和根号)
【答案】
【分析】连接OE,根据∠ABC=90°,AD=,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积-△ABD的面积-△OBE的面积-扇形ODE的面积.
【详解】解:连接OE,过点O作OF⊥BE于点F,
∵∠ABC=90°,AD=,∠ABD=30°,
∴BD=2AD=2,∠ADB=60°,
∴,,
∵AD∥BC,
∴∠DBC=∠ADB=60°,
∵OB=OE,∠DBC=60°,
∴△OBE是等边三角形,
∴BE=OB=,∠BOE=60°,
∴∠DOE=120°,
∵OF⊥BE,
∴,
∴,
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC==2BD=4,
,
故答案为:.
【点睛】本题考查切线的性质,直角梯形,扇形面积的计算,等边三角形的性质与判定,含30度角的直角三角形的性质等等,在计算不规则图形的面积时,常用“切割法”把这个图形分成几个规则图形的和,或者用“拼补法”使它和几个规则图形共同拼凑成一个大的规则图形,用大图形面积减去其它几个图形面积即可.
15.(2021·江苏·苏州高新区实验初级中学)如图,正方形ABCD的边长为4,点E为边AD上一个动点,点F在边CD上,且线段EF=4,点G为线段EF的中点,连接BG、CG,则BG+CG的最小值为 _____.
【答案】5
【分析】因为DG=EF=2,所以G在以D为圆心,2为半径圆上运动,取DI=1,可证△GDI∽△CDG,从而得出GI=CG,然后根据三角形三边关系,得出BI是其最小值
【详解】解:如图,
在Rt△DEF中,G是EF的中点,
∴DG=,
∴点G在以D为圆心,2为半径的圆上运动,
在CD上截取DI=1,连接GI,
∴==,
∴∠GDI=∠CDG,
∴△GDI∽△CDG,
∴=,
∴IG=,
∴BG+=BG+IG≥BI,
∴当B、G、I共线时,BG+CG最小=BI,
在Rt△BCI中,CI=3,BC=4,
∴BI=5,
故答案是:5.
【点睛】本题考查了相似三角形的性质与判定,圆的概念,求得点的运动轨迹是解题的关键.
16.(2021·重庆南开中学)如图,在菱形ABCD中,对角线AC,BD交于点O,AC=4,BD=4,分别以点小点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 _____(结果保留π).
【答案】
【分析】根据菱形的性质得到AC⊥BD,根据直角三角形的性质求出∠ABO=30°,根据扇形面积公式、三角形面积公式计算即可.
【详解】解:∵四边形ABCD是菱形,AC=4,BD=4,
∴AC⊥BD,AO=2,BO=2,
AB=,
∴AB=2AO,
∴∠ABO=30°,∠BAO=∠DAO=60°,
∴阴影部分的面积=×2×4-=4,
故答案为:.
【点睛】本题考查的是扇形面积计算、菱形的性质,掌握扇形面积公式是解题的关键.
17.(2021·重庆江津·)如图,等边△ABC的边长为6,内切圆记为⊙O,P是⊙O上一动点,则2PB+PC的最小值为________.
【答案】
【分析】如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,,首先证明,得到,所以,而(当且仅当、P、共线时取等号),从而计算出得到的最小值.
【详解】解:如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,BO,
为的内切圆,
,
是等边三角形,
,,
,
同理可得
在中,,
∴,
∴,
,
,,,
,
,
,
,
,
的最小值为的长度,
的最小值为的长度,
,,
,
的最小值为.
故答案为:.
【点睛】本题考查了切线的性质、等边三角形的性质以及相似三角形的判定与性质,解决问题的关键是利用相似比确定线段.
18.(2021·北京·人大附中)如图,直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P有 _____个.
【答案】3
【分析】根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
【详解】解:∵直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),
∴A点的坐标为:(﹣2,0),B点的坐标为:(0,2),
∴AB=2,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
∵∠AC1P1=∠AOB=90°,∠C1AP1=∠OAB,
∴△AP1C1∽△ABO,
∴=,即
∴AP1=,
∴P1的坐标为:(﹣2+,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
同理△AP2C2∽△ABO,
∴=,
∴AP2=,
P2的坐标为:(﹣2﹣,0),
从﹣2﹣到﹣2+,整数点有﹣1,﹣2,﹣3,故横坐标为整数的点P的个数是,3个.
故答案为:3.
【点睛】本题考查了一次函数综合题,涉及的知识有:一次函数的图象与性质,切线的性质,一次函数与坐标轴的交点,以及坐标与图形性质,熟悉一次函数的性质和切线的性质是解题的关键.
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.(2021·河南大学附属中学)如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线:
(2)连接CD,则∠A和∠CDE的数量关系为 ;
(3)若∠CDE=27°,OB=2,则的长为 .
【答案】(1)见解析;(2)∠A=2∠CDE;(3)π
【分析】
(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到,然后由弧长的公式即可计算出结果.
【详解】
(1)证明:连接OD,BD,如图,
∵AB是⊙O的切线,
∴AB⊥BC,
∴∠ABO=90°,
∵AB=AD,
∴∠ABD=∠ADB,
∵OB=OD,
∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,即∠ADO=90°,
∴AD⊥OD,
又∵OD是圆O的半径,
∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD,
∴∠DOC=∠A,
∵AD是半圆O的切线,
∴OD⊥AE,
∴∠ODE=90°,
∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,
∴∠DOC=2∠BDO,
∴∠DOC=2∠CDE,
∴∠A=2∠CDE,
故答案为:∠A=2∠CDE;
(3)解:∵∠CDE=27°,
∴∠DOC=2∠CDE=54°,
∴,
∴的长=.
故答案为:π.
【点睛】本题考查了切线是性质,弧长的计算,圆周角定理,等腰三角形的性质,正确的作出辅助线是解题的关键.
20.(2021·江苏·涟水县红日中学)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠E=∠D;
(2)若AB=5,BC-AC=1,求CE的长.
【答案】(1)证明见解析;(2)CE=4
【分析】
(1)因为∠AEC和∠ABC都是的圆周角,故∠AEC=∠ABC,因为AB为直径,故∠ACB=90°,则(SAS),则∠ADC=∠ABC,则∠E=∠D.
(2)由(1)可知为直角三角形,故由勾股定理有,解得AC=3,BC=4,则DC=4,又因为∠E=∠D,故CD=CE=4.
【详解】
(1)∵AB为直径,故∠ACB=90°,CD=BC,AC=AC
∴(SAS)
∴∠D=∠B
又∵∠E=∠B
∴∠E=∠D
(2)由(1)可知为直角三角形,故有
即
解得AC=3,BC=4
则DC=4
又∵∠E=∠D,
故CD=CE=4
【点睛】本题考查了圆与三角形的综合问题,运用圆内角相关性质:同弧所对的圆周角相等,以及直径所对的圆周角等于90°是解题的关键.
21.(2022·黑龙江·哈尔滨市第六十九中学校)如图,内接于,弦AE与弦BC交于点D,连接BO,,
(1)求证:;
(2)若,求的度数;
(3)在(2)的条件下,过点O作于点H,延长HO交AB于点P,若,,求半径的长.
【答案】(1)见解析;(2)30°;(3)
【分析】
(1)如图所示,连接OA,则,由OA=OB,得到∠OAB=∠OBA,即可推出,即∠OBA+∠ACB=90°,再由∠OBA=∠CAE,则∠ACB+∠CAE=90°,由此即可证明;
(2)如图所示,连接CE,则∠ABC=∠AEC,由,可得∠AEC=30°,则∠ABC=30°;
(3)如图所示,过点O作OF⊥AB于F,则BF=AF,设FP=x,可得BP=BF+PF=6+2x,OP=2FP=2x,推出PH=OP+OH=1+2x,则BP=2+4x,从而得到2+4x=6+2x,由此求解即可.
【详解】解:(1)如图所示,连接OA,
∴,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠OAB+∠OBA+∠AOB=180°,
∴,即∠OBA+∠ACB=90°,
又∵∠OBA=∠CAE,
∴∠ACB+∠CAE=90°,
∴∠ADC=90°,
∴AE⊥BC;
(2)如图所示,连接CE,
∴∠ABC=∠AEC,
∵,AE⊥BC,
∴,
∴∠AEC=30°,
∴∠ABC=30°;
(3)如图所示,过点O作OF⊥AB于F,
∴BF=AF,
设FP=x,
∴BF=AF=AP+PF=6+x,
∴BP=BF+PF=6+2x
∵∠ABC=30°,PH⊥BC,
∴∠BPH=60°,BP=2PH,
又∵∠OF⊥AB,
∴∠OFP=90°,
∴∠POF=30°,
∴OP=2FP=2x,
∴PH=OP+OH=1+2x,
∴BP=2+4x,
∴2+4x=6+2x,
解得x=2,
∴PF=2,BF=8,PO=4,
∴,
∴,
∴圆O的半径长为.
【点睛】本题主要考查了圆周角定理,含30度角的直角三角形的性质,等腰三角形的性质,特殊角三角形函数值求度数,勾股定理,垂径定理等等,解题的关键在于能够正确作出辅助线求解.
22.(2021·浙江·绍兴市博雅学校)如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.
(1)求证:BE = CE.
(2)以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积
(3)若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
【答案】(1)见解析(2)扇形FEG的面积为.(3)圆锥的底面圆的半径为.
【分析】
(1)根据条件证明,即可得到结论.
(2)根据(1)的结论以及直角三角形的勾股定理,求出扇形FEG的圆心角以及半径,最后利用公式即可求出面积.
(3)求出扇形FEG的弧长,利用扇形弧长等于其围成的圆锥底面圆的周长,即可求出圆锥的底面圆的半径.
【详解】
(1)证明:由题意可知:,为等边三角形,
点是BC的中点,
是等边的中线,且,
,
,
.
(2)解:如图所示:
与BC相切,且,
点是切点,并且是该扇形的半径,
,且,
,
,
在中,,
,
是BC的中点,
在中,由勾股定理可知:,解得,
扇形FEG的面积为.
(3)解:设圆锥底面圆半径为,
扇形FEG的弧长为: ,
扇形FEG的弧长等于其围成的圆锥的底面圆的周长,
,解得 ,
故圆锥的底面圆的半径为.
【点睛】本题主要是考查了三角形全等,扇形的面积、弧长公式以及扇形与其所围成的圆锥的关系,通过题目所给条件,求解扇形面积公式所需的角度和半径,以及圆锥底面圆所需要的扇形弧长,是求解本题的关键,另外,扇形的面积和弧长公式一定要记牢.
23.(2021·北京市师达中学)如图,、均为同圆中的两条弦,且.
(1)判断与的关系( )
A. B.
C. D.以上三种情况均有可能
(2)若点为的中点,连接并延长交于点,求证:
【答案】(1)B;(2)证明见解析
【分析】
(1)由证明的度数为: 得到组成一个半圆,则也组成一个半圆,从而可得答案;
(2)由为的中点,证明 再证明 从而可得答案.
【详解】解:(1)
的度数为:
即组成一个半圆,
也组成一个半圆,
,
故选B
(2)为的中点,
【点睛】本题考查的是直角三角形斜边上的中线等于斜边的一半,等腰三角形的判定与性质,圆周角与弧之间的关系,熟练的运用以上知识解题是解题的关键.
24.(2021·四川达州·中考真题)如图,是的直径,为上一点(不与点,重合)连接,,过点作,垂足为点.将沿翻折,点落在点处得,交于点.
(1)求证:是的切线;
(2)若,,求阴影部分面积.
【答案】(1)见解析;(2)
【分析】
(1)连接OC,先证明∠CDA=90°,根据折叠的性质和圆的半径相等证明OCAE,从而求出∠ECO=90°,问题得证;
(2)连接,过点作于点,证明四边形OCEG为矩形,求出,,,进而求出,∠COF=30°,分别求出矩形OCEG、△OGF、扇形COF面积,即可求出阴影部分面积.
【详解】解:(1)如图,连接OC,
∵,
∴∠CDA=90°,
∵翻折得到,
∴∠EAC=∠DAC,∠E=∠CDA=90°,
∴∠EAD=2∠DAC,
∵OA=OC,
∴∠OAC=∠OCA
∴∠COD=2∠OAC,
∴∠COD=∠EAD,
∴OCAE,
∴∠ECO=180°-∠E=90°,
∴OC⊥EC,
∴是的切线;
(2)如图,连接,过点作于点,
∵∠E=∠ECO=90°,
∴四边形OCEG为矩形.
∵,,
∴,
∴,
∴,
∵于点,OA=OF=2,
∴,∠FAO=∠AFO=30°,
∵OCAE,
∴∠COF=∠AFO=30°,
∴矩形OCEG面积为,
△OGF面积为,
扇形COF面积为
∴阴影部分面积=矩形OCEG面积-△OGF面积-扇形COF面积=.
【点睛】本题为圆的综合题,考查了切线的判定,垂径定理,扇形的面积等知识,综合性较强,熟练掌握相关定理并根据题意添加辅助线是解题的关键.
25.(2021·湖南株洲·中考真题)如图所示,是的直径,点、是上不同的两点,直线交线段于点,交过点的直线于点,若,且.
(1)求证:直线是的切线;
(2)连接、、、,若.
①求证:;
②过点作,交线段于点,点为线段的中点,若,求线段的长度.
【答案】(1)证明见解析;(2)①证明见解析;②1
【分析】
(1)先将转化为,再利用勾股定理逆定理证明即可;
(2)①利用同一条弧所对的圆周角等于其所对圆心角的一半和同一条弧所对的圆周角相等分别得到与,再利用两角分别相等的两三角形相似即可完成求证;
②分别利用相似三角形的性质和平行线分线段成比例定理的推论求出AC的长和CG的长,最后利用线段的和差关系求解即可.
【详解】解:(1)证:因为,且,
∴,
∴,
∴,
∴直线是的切线;
(2)①∵,
又∵,
∴,
∵,
∴.;
②∵,
∴,
设圆的半径为r,
∵, ,
∴,
∴;
∵点为线段的中点,
∴,
∵,
∴,
∴,
∴,
∴线段的长度为1.
【点睛】本题综合考查了切线的判定定理、圆周角定理及其推论、勾股定理逆定理、相似三角形的判定与性质、平行线分线段成比例定理的推论等内容,解决本题的关键是牢记相关概念,能根据题意建立相等关系等,本题考查内容较多,综合性较强,对学生的综合分析能力有较高要求.
一、选择题:本题共10个小题,每小题3分,共30分。
1.已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O有公共点( ).
A.0个 B.1个 C.2个 D.无法确定
2.若⊙P的半径为5,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
3.用一个圆心角为,半径为12的扇形作为一个圆锥的侧面,则该圆锥底面半径为( )
A. B.4 C.6 D.8
4.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
5.如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
A.50° B.55° C.65° D.75°
6.如图所示,⊙O的半径为5,点O到直线l的距离为7,P是直线l上的一个动点,PQ与⊙O相切于点Q.则PQ的最小值为( )
A. B. C.2 D.2
7.如图,△ABC中.∠C=90°,点D是边BC上一个动点(点D不与点C重合).以CD为直径的圆交AD于点P.若AC=6.线段BP长度的最小值是2.则AB的长为( )
A.8 B.2 C.4 D.2
8.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么弧AC所对的圆心角的大小是( )
A.45° B.60° C.80° D.90°
9.若随意向如图所示的正方形内抛一粒石子,则石子落在阴影部分的概率是( )
A.1 B.1 C. D.1
10.矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A.3.6 B. C.3.5 D.
二、填空题:本题共8个小题,每题3分,共24分。
11.已知:⊙O的半径OA=4,点A、B、C为圆上不重合的三个点,弦AB的长为4,则∠ACB=_____.
12.已知正五边形的外接圆直径为6,那么该正五边形外接圆的半径为_____.
13.Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,则以2.6cm为半径的⊙C与直线AB的位置关系是__________.
14.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD= ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为_____________.(结果保留π和根号)
15.如图,正方形ABCD的边长为4,点E为边AD上一个动点,点F在边CD上,且线段EF=4,点G为线段EF的中点,连接BG、CG,则BG+CG的最小值为 _____.
16.如图,在菱形ABCD中,对角线AC,BD交于点O,AC=4,BD=4,分别以点小点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 _____(结果保留π).
17.如图,等边△ABC的边长为6,内切圆记为⊙O,P是⊙O上一动点,则2PB+PC的最小值为________.
18.如图,直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P有 _____个.
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线:
(2)连接CD,则∠A和∠CDE的数量关系为 ;
(3)若∠CDE=27°,OB=2,则的长为 .
20.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠E=∠D;
(2)若AB=5,BC-AC=1,求CE的长.
21.如图,内接于,弦AE与弦BC交于点D,连接BO,,
(1)求证:;
(2)若,求的度数;
(3)在(2)的条件下,过点O作于点H,延长HO交AB于点P,若,,求半径的长.
22.如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.
(1)求证:BE = CE.
(2)以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积
(3)若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
23.如图,是的直径,为上一点(不与点,重合)连接,,过点作,垂足为点.将沿翻折,点落在点处得,交于点.
(1)求证:是的切线;
(2)若,,求阴影部分面积.
24.如图所示,是的直径,点、是上不同的两点,直线交线段于点,交过点的直线于点,若,且.
(1)求证:直线是的切线;
(2)连接、、、,若.
①求证:;
②过点作,交线段于点,点为线段的中点,若,求线段的长度.
答案
一、选择题
1.C
【分析】根据⊙O半径为5,点O到直线l的距离为3得到直线l与⊙O相交,即可判断出直线l与⊙O有两个公共点.
【详解】解:∵⊙O半径为5,点O到直线l的距离为3,
∴d<r,
∴直线l与⊙O相交,
∴直线l与⊙O有两个公共点.
故选:C
2.B
【分析】由勾股定理等性质算出点与圆心的距离,则时,点在圆外;当时,点在圆上;当时,点在圆内.
【详解】解:由勾股定理,得
,
,
原点在上.
故选:B.
3.B
【分析】根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
【详解】解:设圆锥底面的半径为,
扇形的弧长为:,
圆锥的底面周长等于它的侧面展开图的弧长,
根据题意得,
解得:.
故选:B.
4.C
【分析】根据题意连接OC,依据切线性质得出,进而利用勾股定理即可求出PC.
【详解】解:连接OC,
∵PC为⊙O的切线,
∴,
∵OB=OC=3,PB=2,
∴,
∴.
故选:C.
5.C
【分析】首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
6.C
【分析】由切线的性质可知OQ⊥PQ,在Rt△OPQ中,OQ=5,则可知当OP最小时,PQ有最小值,当OP⊥l时,OP最小,利用勾股定理可求得PQ的最小值.
【详解】解:∵PQ与⊙O相切于点Q,
∴OQ⊥PQ,
∴PQ2=OP2-OQ2=OP2-52=OP2-25,
∴当OP最小时,PQ有最小值,
∵点O到直线l的距离为7,
∴OP的最小值为7,
∴PQ的最小值=,
故选:C.
7.D
【分析】利用圆周角定理得到∠CPD=90°,则可判断点P在以AC为直径的⊙O上,如图,连接OB交⊙O于P′,利用点与圆的位置关系得到BP′=2,再利用勾股定理计算出BC,然后在Rt△ABC中利用勾股定理可计算出AB.
【详解】解:∵CD为直径,
∴∠CPD=90°,
∵∠APC=90°,
∴点P在以AC为直径的⊙O上,如图,
连接OB交⊙O于P′,
∵线段BP长度的最小值是2,
∴BP′=2,
∴OB=2+3=5,
在Rt△OBC中,BC=,
在Rt△ABC中,AB=.
故选:D.
8.D
【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,分别作AB,BC的垂直平分线即可得到圆心,进而解答即可.
【详解】解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即弧AC所对的圆心角是90°,
故选:D.
9.A
【分析】设正方形ABCD的边长为a,然后根据石子落在阴影部分的概率即为阴影部分面积与正方形面积的比,由此进行求解即可.
【详解】解:如图所示,设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴∠C=90°,
∴
,
∴,
∴石子落在阴影部分的概率是,
故选A.
10.A
【分析】连接ON、OG、OF,作OH⊥CD于H,在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,可得FN的值,设FG=x,由OG2=ON2-GN2=OF2-FG2,可得FG的值,进而即可求解.
【详解】解:连接ON、OG、OF,作OH⊥CD于H,
∵点O是矩形对称中心,矩形沿MN折叠,使点C恰好落在AD边的中点F处,
∴DH=HC=CD=6,OF=AB=6,
∵以O为圆心的圆与NF相切,
∴OG⊥NF,
由折叠的性质可知,NC=NF,
在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,
解得,FN=,
∴DN=12-=,
∴HN=HD-DN=6-=,
设FG=x,则NG=-x,
∵OG2=ON2-GN2=OF2-FG2,
即42+()2-(-x)2=62-x2,
解得,x=4.8,
∴OG=
故选:A.
二、填空题:。
11.45°或135°135°或45°
【分析】根据题意画出图形,先判断出∠AOB=90°,再分两种情况用同弧所对的圆心角和圆周角的关系确定和圆的内接四边形的性质即可.
【详解】解:如图,
∵OA=OB=4,AB=4,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
当点C在优弧上时,∠ACB=∠AOB=45°,
点C在劣弧上时,∠AC'B+∠ACB=180°,
∴∠AC'B=180°﹣45°=135°,
∴∠ACB=45°或135°,
故答案为45°或135°.
12.3
【分析】根据半径是直径的一半直接写出答案即可.
【详解】解:∵正五边形的外接圆直径为6,
∴该正五边形外接圆的半径为6÷2=3,
故答案为:3.
13.相交
【分析】由勾股定理可求AB的长度,根据三角形的面积公式可求点C到直线AB的距离,即可判断⊙C与直线AB的位置关系.
【详解】解:∵∠C=90°,AC=4,BC=3,
∴AB==5,
设点C到直线AB的距离为d,
∵S△ABC=AB×d=×AC×BC
∴5d=12
∴d=
∵d<r=2.6
∴⊙C与直线AB的位置关系为相交,
故答案为:相交.
14.
【分析】连接OE,根据∠ABC=90°,AD=,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积-△ABD的面积-△OBE的面积-扇形ODE的面积.
【详解】解:连接OE,过点O作OF⊥BE于点F,
∵∠ABC=90°,AD=,∠ABD=30°,
∴BD=2AD=2,∠ADB=60°,
∴,,
∵AD∥BC,
∴∠DBC=∠ADB=60°,
∵OB=OE,∠DBC=60°,
∴△OBE是等边三角形,
∴BE=OB=,∠BOE=60°,
∴∠DOE=120°,
∵OF⊥BE,
∴,
∴,
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC==2BD=4,
,
故答案为:.
15.5
【分析】因为DG=EF=2,所以G在以D为圆心,2为半径圆上运动,取DI=1,可证△GDI∽△CDG,从而得出GI=CG,然后根据三角形三边关系,得出BI是其最小值
【详解】解:如图,
在Rt△DEF中,G是EF的中点,
∴DG=,
∴点G在以D为圆心,2为半径的圆上运动,
在CD上截取DI=1,连接GI,
∴==,
∴∠GDI=∠CDG,
∴△GDI∽△CDG,
∴=,
∴IG=,
∴BG+=BG+IG≥BI,
∴当B、G、I共线时,BG+CG最小=BI,
在Rt△BCI中,CI=3,BC=4,
∴BI=5,
故答案是:5.
16.
【分析】根据菱形的性质得到AC⊥BD,根据直角三角形的性质求出∠ABO=30°,根据扇形面积公式、三角形面积公式计算即可.
【详解】解:∵四边形ABCD是菱形,AC=4,BD=4,
∴AC⊥BD,AO=2,BO=2,
AB=,
∴AB=2AO,
∴∠ABO=30°,∠BAO=∠DAO=60°,
∴阴影部分的面积=×2×4-=4,
故答案为:.
17.
【分析】如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,,首先证明,得到,所以,而(当且仅当、P、共线时取等号),从而计算出得到的最小值.
【详解】解:如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,BO,
为的内切圆,
,
是等边三角形,
,,
,
同理可得
在中,,
∴,
∴,
,
,,,
,
,
,
,
,
的最小值为的长度,
的最小值为的长度,
,,
,
的最小值为.
故答案为:.
18.3
【分析】根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
【详解】解:∵直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),
∴A点的坐标为:(﹣2,0),B点的坐标为:(0,2),
∴AB=2,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
∵∠AC1P1=∠AOB=90°,∠C1AP1=∠OAB,
∴△AP1C1∽△ABO,
∴=,即
∴AP1=,
∴P1的坐标为:(﹣2+,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
同理△AP2C2∽△ABO,
∴=,
∴AP2=,
P2的坐标为:(﹣2﹣,0),
从﹣2﹣到﹣2+,整数点有﹣1,﹣2,﹣3,故横坐标为整数的点P的个数是,3个.
故答案为:3.
三、解答题。
19.
(1)证明:连接OD,BD,如图,
∵AB是⊙O的切线,
∴AB⊥BC,
∴∠ABO=90°,
∵AB=AD,
∴∠ABD=∠ADB,
∵OB=OD,
∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,即∠ADO=90°,
∴AD⊥OD,
又∵OD是圆O的半径,
∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD,
∴∠DOC=∠A,
∵AD是半圆O的切线,
∴OD⊥AE,
∴∠ODE=90°,
∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,
∴∠DOC=2∠BDO,
∴∠DOC=2∠CDE,
∴∠A=2∠CDE,
故答案为:∠A=2∠CDE;
(3)解:∵∠CDE=27°,
∴∠DOC=2∠CDE=54°,
∴,
∴的长=.
故答案为:π.
20.
(1)∵AB为直径,故∠ACB=90°,CD=BC,AC=AC
∴(SAS)
∴∠D=∠B
又∵∠E=∠B
∴∠E=∠D
(2)由(1)可知为直角三角形,故有
即
解得AC=3,BC=4
则DC=4
又∵∠E=∠D,
故CD=CE=4
21.解:(1)如图所示,连接OA,
∴,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠OAB+∠OBA+∠AOB=180°,
∴,即∠OBA+∠ACB=90°,
又∵∠OBA=∠CAE,
∴∠ACB+∠CAE=90°,
∴∠ADC=90°,
∴AE⊥BC;
(2)如图所示,连接CE,
∴∠ABC=∠AEC,
∵,AE⊥BC,
∴,
∴∠AEC=30°,
∴∠ABC=30°;
(3)如图所示,过点O作OF⊥AB于F,
∴BF=AF,
设FP=x,
∴BF=AF=AP+PF=6+x,
∴BP=BF+PF=6+2x
∵∠ABC=30°,PH⊥BC,
∴∠BPH=60°,BP=2PH,
又∵∠OF⊥AB,
∴∠OFP=90°,
∴∠POF=30°,
∴OP=2FP=2x,
∴PH=OP+OH=1+2x,
∴BP=2+4x,
∴2+4x=6+2x,
解得x=2,
∴PF=2,BF=8,PO=4,
∴,
∴,
∴圆O的半径长为.
22.
(1)证明:由题意可知:,为等边三角形,
点是BC的中点,
是等边的中线,且,
,
,
.
(2)解:如图所示:
与BC相切,且,
点是切点,并且是该扇形的半径,
,且,
,
,
在中,,
,
是BC的中点,
在中,由勾股定理可知:,解得,
扇形FEG的面积为.
(3)解:设圆锥底面圆半径为,
扇形FEG的弧长为: ,
扇形FEG的弧长等于其围成的圆锥的底面圆的周长,
,解得 ,
故圆锥的底面圆的半径为.
23.解:(1)如图,连接OC,
∵,
∴∠CDA=90°,
∵翻折得到,
∴∠EAC=∠DAC,∠E=∠CDA=90°,
∴∠EAD=2∠DAC,
∵OA=OC,
∴∠OAC=∠OCA
∴∠COD=2∠OAC,
∴∠COD=∠EAD,
∴OCAE,
∴∠ECO=180°-∠E=90°,
∴OC⊥EC,
∴是的切线;
(2)如图,连接,过点作于点,
∵∠E=∠ECO=90°,
∴四边形OCEG为矩形.
∵,,
∴,
∴,
∴,
∵于点,OA=OF=2,
∴,∠FAO=∠AFO=30°,
∵OCAE,
∴∠COF=∠AFO=30°,
∴矩形OCEG面积为,
△OGF面积为,
扇形COF面积为
∴阴影部分面积=矩形OCEG面积-△OGF面积-扇形COF面积=.
24.解:(1)证:因为,且,
∴,
∴,
∴,
∴直线是的切线;
(2)①∵,
又∵,
∴,
∵,
∴.;
②∵,
∴,
设圆的半径为r,
∵, ,
∴,
∴;
∵点为线段的中点,
∴,
∵,
∴,
∴,
∴,
∴线段的长度为1.
【高效培优】2021—2022学年沪教版九年级数学下册轻松冲刺学神考霸必刷卷
【期中满分押题】夯实基础过关卷
(考试范围:第二十七章 考试时间:120分钟 试卷满分:120分)
学校:___________姓名:___________班级:___________考号:___________
本卷试题共三大题,共25小题,单选10题,填空8题,解答7题,限时120分钟,满分120分,本卷题型精选核心常考重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!
选择题:本题共10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2021·全国·中考真题)已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O有公共点( ).
A.0个 B.1个 C.2个 D.无法确定
【答案】C
【分析】根据⊙O半径为5,点O到直线l的距离为3得到直线l与⊙O相交,即可判断出直线l与⊙O有两个公共点.
【详解】解:∵⊙O半径为5,点O到直线l的距离为3,
∴d<r,
∴直线l与⊙O相交,
∴直线l与⊙O有两个公共点.
故选:C
【点睛】本题考查了直线与圆的位置关系,能根据圆心到直线的距离d与圆的半径r关系判断位置关系是解题关键.当d>r时,直线与圆相离,没有公共点,当d=r时,直线与圆相切,有一个公共点,当d<r时,直线与圆相交,有两个公共点.
2.(2021·上海·九年级期末)若⊙P的半径为5,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
【答案】B
【分析】由勾股定理等性质算出点与圆心的距离,则时,点在圆外;当时,点在圆上;当时,点在圆内.
【详解】解:由勾股定理,得
,
,
原点在上.
故选:B.
【点睛】本题考查了点与圆的位置关系,解题的关键是要记住若半径为,点到圆心的距离为,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.
3.(2021·天津·九年级期末)用一个圆心角为,半径为12的扇形作为一个圆锥的侧面,则该圆锥底面半径为( )
A. B.4 C.6 D.8
【答案】B
【分析】根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
【详解】解:设圆锥底面的半径为,
扇形的弧长为:,
圆锥的底面周长等于它的侧面展开图的弧长,
根据题意得,
解得:.
故选:B.
【点睛】本题考查的是圆锥的计算,解题的关键是掌握弧长公式、周长公式和圆锥与扇形的对应关系.
4.(2021·山东·日照港中学)如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
【答案】C
【分析】根据题意连接OC,依据切线性质得出,进而利用勾股定理即可求出PC.
【详解】解:连接OC,
∵PC为⊙O的切线,
∴,
∵OB=OC=3,PB=2,
∴,
∴.
故选:C.
【点睛】本题考查切线的性质,熟练掌握切线的性质以及勾股定理的运用是解题的关键.
5.(2021·安徽淮南·)如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
A.50° B.55° C.65° D.75°
【答案】C
【分析】首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
6.(2021·浙江·绍兴市博雅学校)如图所示,⊙O的半径为5,点O到直线l的距离为7,P是直线l上的一个动点,PQ与⊙O相切于点Q.则PQ的最小值为( )
A. B. C.2 D.2
【答案】C
【分析】由切线的性质可知OQ⊥PQ,在Rt△OPQ中,OQ=5,则可知当OP最小时,PQ有最小值,当OP⊥l时,OP最小,利用勾股定理可求得PQ的最小值.
【详解】解:∵PQ与⊙O相切于点Q,
∴OQ⊥PQ,
∴PQ2=OP2-OQ2=OP2-52=OP2-25,
∴当OP最小时,PQ有最小值,
∵点O到直线l的距离为7,
∴OP的最小值为7,
∴PQ的最小值=,
故选:C.
【点睛】本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键.
7.(2021·浙江·杭州市公益中学)如图,△ABC中.∠C=90°,点D是边BC上一个动点(点D不与点C重合).以CD为直径的圆交AD于点P.若AC=6.线段BP长度的最小值是2.则AB的长为( )
A.8 B.2 C.4 D.2
【答案】D
【分析】利用圆周角定理得到∠CPD=90°,则可判断点P在以AC为直径的⊙O上,如图,连接OB交⊙O于P′,利用点与圆的位置关系得到BP′=2,再利用勾股定理计算出BC,然后在Rt△ABC中利用勾股定理可计算出AB.
【详解】解:∵CD为直径,
∴∠CPD=90°,
∵∠APC=90°,
∴点P在以AC为直径的⊙O上,如图,
连接OB交⊙O于P′,
∵线段BP长度的最小值是2,
∴BP′=2,
∴OB=2+3=5,
在Rt△OBC中,BC=,
在Rt△ABC中,AB=.
故选:D.
【点睛】本题主要考查了圆周角定理,点与圆的位置关系,勾股定理,准确计算是解题的关键.
8.(2022·黑龙江·大庆市第三十六中学)如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么弧AC所对的圆心角的大小是( )
A.45° B.60° C.80° D.90°
【答案】D
【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,分别作AB,BC的垂直平分线即可得到圆心,进而解答即可.
【详解】解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即弧AC所对的圆心角是90°,
故选:D.
【点睛】本题考查了垂径定理的推论:弦的垂直平分线必过圆心.这也是常用来确定圆心的方法.
9.(2021·贵州黔西·)若随意向如图所示的正方形内抛一粒石子,则石子落在阴影部分的概率是( )
A.1 B.1 C. D.1
【答案】A
【分析】设正方形ABCD的边长为a,然后根据石子落在阴影部分的概率即为阴影部分面积与正方形面积的比,由此进行求解即可.
【详解】解:如图所示,设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴∠C=90°,
∴
,
∴,
∴石子落在阴影部分的概率是,
故选A.
【点睛】本题主要考查了几何概率,正方形的性质,扇形面积公式,解题的关键在于能够根据题意得到石子落在阴影部分的概率即为阴影部分面积与正方形面积的比.
10.(2021·湖北·武汉七一华源中学)矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A.3.6 B. C.3.5 D.
【答案】A
【分析】连接ON、OG、OF,作OH⊥CD于H,在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,可得FN的值,设FG=x,由OG2=ON2-GN2=OF2-FG2,可得FG的值,进而即可求解.
【详解】解:连接ON、OG、OF,作OH⊥CD于H,
∵点O是矩形对称中心,矩形沿MN折叠,使点C恰好落在AD边的中点F处,
∴DH=HC=CD=6,OF=AB=6,
∵以O为圆心的圆与NF相切,
∴OG⊥NF,
由折叠的性质可知,NC=NF,
在Rt△FDN中,FN2=DF2+ND2,即FN2=(12-FN)2+42,
解得,FN=,
∴DN=12-=,
∴HN=HD-DN=6-=,
设FG=x,则NG=-x,
∵OG2=ON2-GN2=OF2-FG2,
即42+()2-(-x)2=62-x2,
解得,x=4.8,
∴OG=
故选:A.
【点睛】本题主要考查圆的切线的性质,矩形的性质,折叠的性质,勾股定理,添加辅助线,构造直角三角形是解题的关键.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·北京·人大附中)已知:⊙O的半径OA=4,点A、B、C为圆上不重合的三个点,弦AB的长为4,则∠ACB=_____.
【答案】45°或135°135°或45°
【分析】根据题意画出图形,先判断出∠AOB=90°,再分两种情况用同弧所对的圆心角和圆周角的关系确定和圆的内接四边形的性质即可.
【详解】解:如图,
∵OA=OB=4,AB=4,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
当点C在优弧上时,∠ACB=∠AOB=45°,
点C在劣弧上时,∠AC'B+∠ACB=180°,
∴∠AC'B=180°﹣45°=135°,
∴∠ACB=45°或135°,
故答案为45°或135°.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
12.(2021·陕西咸阳·)已知正五边形的外接圆直径为6,那么该正五边形外接圆的半径为_____.
【答案】3
【分析】根据半径是直径的一半直接写出答案即可.
【详解】解:∵正五边形的外接圆直径为6,
∴该正五边形外接圆的半径为6÷2=3,
故答案为:3.
【点睛】本题考查了正多边形和圆的知识,知道等圆或同圆中直径是半径的2倍是解答本题的关键.
13.(2021·重庆江津·)Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,则以2.6cm为半径的⊙C与直线AB的位置关系是__________.
【答案】相交
【分析】由勾股定理可求AB的长度,根据三角形的面积公式可求点C到直线AB的距离,即可判断⊙C与直线AB的位置关系.
【详解】解:∵∠C=90°,AC=4,BC=3,
∴AB==5,
设点C到直线AB的距离为d,
∵S△ABC=AB×d=×AC×BC
∴5d=12
∴d=
∵d<r=2.6
∴⊙C与直线AB的位置关系为相交,
故答案为:相交.
【点睛】本题考查直线与圆的位置关系,勾股定理,三角形的面积公式,若设⊙O的半径为r,圆心O到直线l的距离为d,则①直线l和⊙O相交 d<r,②直线l和⊙O相切 d=r,③直线l和⊙O相离 d>r.
14.(2021·甘肃·金昌市第五中学)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD= ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为_____________.(结果保留π和根号)
【答案】
【分析】连接OE,根据∠ABC=90°,AD=,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积-△ABD的面积-△OBE的面积-扇形ODE的面积.
【详解】解:连接OE,过点O作OF⊥BE于点F,
∵∠ABC=90°,AD=,∠ABD=30°,
∴BD=2AD=2,∠ADB=60°,
∴,,
∵AD∥BC,
∴∠DBC=∠ADB=60°,
∵OB=OE,∠DBC=60°,
∴△OBE是等边三角形,
∴BE=OB=,∠BOE=60°,
∴∠DOE=120°,
∵OF⊥BE,
∴,
∴,
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC==2BD=4,
,
故答案为:.
【点睛】本题考查切线的性质,直角梯形,扇形面积的计算,等边三角形的性质与判定,含30度角的直角三角形的性质等等,在计算不规则图形的面积时,常用“切割法”把这个图形分成几个规则图形的和,或者用“拼补法”使它和几个规则图形共同拼凑成一个大的规则图形,用大图形面积减去其它几个图形面积即可.
15.(2021·江苏·苏州高新区实验初级中学)如图,正方形ABCD的边长为4,点E为边AD上一个动点,点F在边CD上,且线段EF=4,点G为线段EF的中点,连接BG、CG,则BG+CG的最小值为 _____.
【答案】5
【分析】因为DG=EF=2,所以G在以D为圆心,2为半径圆上运动,取DI=1,可证△GDI∽△CDG,从而得出GI=CG,然后根据三角形三边关系,得出BI是其最小值
【详解】解:如图,
在Rt△DEF中,G是EF的中点,
∴DG=,
∴点G在以D为圆心,2为半径的圆上运动,
在CD上截取DI=1,连接GI,
∴==,
∴∠GDI=∠CDG,
∴△GDI∽△CDG,
∴=,
∴IG=,
∴BG+=BG+IG≥BI,
∴当B、G、I共线时,BG+CG最小=BI,
在Rt△BCI中,CI=3,BC=4,
∴BI=5,
故答案是:5.
【点睛】本题考查了相似三角形的性质与判定,圆的概念,求得点的运动轨迹是解题的关键.
16.(2021·重庆南开中学)如图,在菱形ABCD中,对角线AC,BD交于点O,AC=4,BD=4,分别以点小点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 _____(结果保留π).
【答案】
【分析】根据菱形的性质得到AC⊥BD,根据直角三角形的性质求出∠ABO=30°,根据扇形面积公式、三角形面积公式计算即可.
【详解】解:∵四边形ABCD是菱形,AC=4,BD=4,
∴AC⊥BD,AO=2,BO=2,
AB=,
∴AB=2AO,
∴∠ABO=30°,∠BAO=∠DAO=60°,
∴阴影部分的面积=×2×4-=4,
故答案为:.
【点睛】本题考查的是扇形面积计算、菱形的性质,掌握扇形面积公式是解题的关键.
17.(2021·重庆江津·)如图,等边△ABC的边长为6,内切圆记为⊙O,P是⊙O上一动点,则2PB+PC的最小值为________.
【答案】
【分析】如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,,首先证明,得到,所以,而(当且仅当、P、共线时取等号),从而计算出得到的最小值.
【详解】解:如图,连接交于点,取的中点,延长CO与AB交于G,连接,,,BO,
为的内切圆,
,
是等边三角形,
,,
,
同理可得
在中,,
∴,
∴,
,
,,,
,
,
,
,
,
的最小值为的长度,
的最小值为的长度,
,,
,
的最小值为.
故答案为:.
【点睛】本题考查了切线的性质、等边三角形的性质以及相似三角形的判定与性质,解决问题的关键是利用相似比确定线段.
18.(2021·北京·人大附中)如图,直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P有 _____个.
【答案】3
【分析】根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
【详解】解:∵直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),
∴A点的坐标为:(﹣2,0),B点的坐标为:(0,2),
∴AB=2,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
∵∠AC1P1=∠AOB=90°,∠C1AP1=∠OAB,
∴△AP1C1∽△ABO,
∴=,即
∴AP1=,
∴P1的坐标为:(﹣2+,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
同理△AP2C2∽△ABO,
∴=,
∴AP2=,
P2的坐标为:(﹣2﹣,0),
从﹣2﹣到﹣2+,整数点有﹣1,﹣2,﹣3,故横坐标为整数的点P的个数是,3个.
故答案为:3.
【点睛】本题考查了一次函数综合题,涉及的知识有:一次函数的图象与性质,切线的性质,一次函数与坐标轴的交点,以及坐标与图形性质,熟悉一次函数的性质和切线的性质是解题的关键.
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.(2021·河南大学附属中学)如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线:
(2)连接CD,则∠A和∠CDE的数量关系为 ;
(3)若∠CDE=27°,OB=2,则的长为 .
【答案】(1)见解析;(2)∠A=2∠CDE;(3)π
【分析】
(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到,然后由弧长的公式即可计算出结果.
【详解】
(1)证明:连接OD,BD,如图,
∵AB是⊙O的切线,
∴AB⊥BC,
∴∠ABO=90°,
∵AB=AD,
∴∠ABD=∠ADB,
∵OB=OD,
∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,即∠ADO=90°,
∴AD⊥OD,
又∵OD是圆O的半径,
∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD,
∴∠DOC=∠A,
∵AD是半圆O的切线,
∴OD⊥AE,
∴∠ODE=90°,
∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,
∴∠DOC=2∠BDO,
∴∠DOC=2∠CDE,
∴∠A=2∠CDE,
故答案为:∠A=2∠CDE;
(3)解:∵∠CDE=27°,
∴∠DOC=2∠CDE=54°,
∴,
∴的长=.
故答案为:π.
【点睛】本题考查了切线是性质,弧长的计算,圆周角定理,等腰三角形的性质,正确的作出辅助线是解题的关键.
20.(2021·江苏·涟水县红日中学)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠E=∠D;
(2)若AB=5,BC-AC=1,求CE的长.
【答案】(1)证明见解析;(2)CE=4
【分析】
(1)因为∠AEC和∠ABC都是的圆周角,故∠AEC=∠ABC,因为AB为直径,故∠ACB=90°,则(SAS),则∠ADC=∠ABC,则∠E=∠D.
(2)由(1)可知为直角三角形,故由勾股定理有,解得AC=3,BC=4,则DC=4,又因为∠E=∠D,故CD=CE=4.
【详解】
(1)∵AB为直径,故∠ACB=90°,CD=BC,AC=AC
∴(SAS)
∴∠D=∠B
又∵∠E=∠B
∴∠E=∠D
(2)由(1)可知为直角三角形,故有
即
解得AC=3,BC=4
则DC=4
又∵∠E=∠D,
故CD=CE=4
【点睛】本题考查了圆与三角形的综合问题,运用圆内角相关性质:同弧所对的圆周角相等,以及直径所对的圆周角等于90°是解题的关键.
21.(2022·黑龙江·哈尔滨市第六十九中学校)如图,内接于,弦AE与弦BC交于点D,连接BO,,
(1)求证:;
(2)若,求的度数;
(3)在(2)的条件下,过点O作于点H,延长HO交AB于点P,若,,求半径的长.
【答案】(1)见解析;(2)30°;(3)
【分析】
(1)如图所示,连接OA,则,由OA=OB,得到∠OAB=∠OBA,即可推出,即∠OBA+∠ACB=90°,再由∠OBA=∠CAE,则∠ACB+∠CAE=90°,由此即可证明;
(2)如图所示,连接CE,则∠ABC=∠AEC,由,可得∠AEC=30°,则∠ABC=30°;
(3)如图所示,过点O作OF⊥AB于F,则BF=AF,设FP=x,可得BP=BF+PF=6+2x,OP=2FP=2x,推出PH=OP+OH=1+2x,则BP=2+4x,从而得到2+4x=6+2x,由此求解即可.
【详解】解:(1)如图所示,连接OA,
∴,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠OAB+∠OBA+∠AOB=180°,
∴,即∠OBA+∠ACB=90°,
又∵∠OBA=∠CAE,
∴∠ACB+∠CAE=90°,
∴∠ADC=90°,
∴AE⊥BC;
(2)如图所示,连接CE,
∴∠ABC=∠AEC,
∵,AE⊥BC,
∴,
∴∠AEC=30°,
∴∠ABC=30°;
(3)如图所示,过点O作OF⊥AB于F,
∴BF=AF,
设FP=x,
∴BF=AF=AP+PF=6+x,
∴BP=BF+PF=6+2x
∵∠ABC=30°,PH⊥BC,
∴∠BPH=60°,BP=2PH,
又∵∠OF⊥AB,
∴∠OFP=90°,
∴∠POF=30°,
∴OP=2FP=2x,
∴PH=OP+OH=1+2x,
∴BP=2+4x,
∴2+4x=6+2x,
解得x=2,
∴PF=2,BF=8,PO=4,
∴,
∴,
∴圆O的半径长为.
【点睛】本题主要考查了圆周角定理,含30度角的直角三角形的性质,等腰三角形的性质,特殊角三角形函数值求度数,勾股定理,垂径定理等等,解题的关键在于能够正确作出辅助线求解.
22.(2021·浙江·绍兴市博雅学校)如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.
(1)求证:BE = CE.
(2)以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积
(3)若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
【答案】(1)见解析(2)扇形FEG的面积为.(3)圆锥的底面圆的半径为.
【分析】
(1)根据条件证明,即可得到结论.
(2)根据(1)的结论以及直角三角形的勾股定理,求出扇形FEG的圆心角以及半径,最后利用公式即可求出面积.
(3)求出扇形FEG的弧长,利用扇形弧长等于其围成的圆锥底面圆的周长,即可求出圆锥的底面圆的半径.
【详解】
(1)证明:由题意可知:,为等边三角形,
点是BC的中点,
是等边的中线,且,
,
,
.
(2)解:如图所示:
与BC相切,且,
点是切点,并且是该扇形的半径,
,且,
,
,
在中,,
,
是BC的中点,
在中,由勾股定理可知:,解得,
扇形FEG的面积为.
(3)解:设圆锥底面圆半径为,
扇形FEG的弧长为: ,
扇形FEG的弧长等于其围成的圆锥的底面圆的周长,
,解得 ,
故圆锥的底面圆的半径为.
【点睛】本题主要是考查了三角形全等,扇形的面积、弧长公式以及扇形与其所围成的圆锥的关系,通过题目所给条件,求解扇形面积公式所需的角度和半径,以及圆锥底面圆所需要的扇形弧长,是求解本题的关键,另外,扇形的面积和弧长公式一定要记牢.
23.(2021·北京市师达中学)如图,、均为同圆中的两条弦,且.
(1)判断与的关系( )
A. B.
C. D.以上三种情况均有可能
(2)若点为的中点,连接并延长交于点,求证:
【答案】(1)B;(2)证明见解析
【分析】
(1)由证明的度数为: 得到组成一个半圆,则也组成一个半圆,从而可得答案;
(2)由为的中点,证明 再证明 从而可得答案.
【详解】解:(1)
的度数为:
即组成一个半圆,
也组成一个半圆,
,
故选B
(2)为的中点,
【点睛】本题考查的是直角三角形斜边上的中线等于斜边的一半,等腰三角形的判定与性质,圆周角与弧之间的关系,熟练的运用以上知识解题是解题的关键.
24.(2021·四川达州·中考真题)如图,是的直径,为上一点(不与点,重合)连接,,过点作,垂足为点.将沿翻折,点落在点处得,交于点.
(1)求证:是的切线;
(2)若,,求阴影部分面积.
【答案】(1)见解析;(2)
【分析】
(1)连接OC,先证明∠CDA=90°,根据折叠的性质和圆的半径相等证明OCAE,从而求出∠ECO=90°,问题得证;
(2)连接,过点作于点,证明四边形OCEG为矩形,求出,,,进而求出,∠COF=30°,分别求出矩形OCEG、△OGF、扇形COF面积,即可求出阴影部分面积.
【详解】解:(1)如图,连接OC,
∵,
∴∠CDA=90°,
∵翻折得到,
∴∠EAC=∠DAC,∠E=∠CDA=90°,
∴∠EAD=2∠DAC,
∵OA=OC,
∴∠OAC=∠OCA
∴∠COD=2∠OAC,
∴∠COD=∠EAD,
∴OCAE,
∴∠ECO=180°-∠E=90°,
∴OC⊥EC,
∴是的切线;
(2)如图,连接,过点作于点,
∵∠E=∠ECO=90°,
∴四边形OCEG为矩形.
∵,,
∴,
∴,
∴,
∵于点,OA=OF=2,
∴,∠FAO=∠AFO=30°,
∵OCAE,
∴∠COF=∠AFO=30°,
∴矩形OCEG面积为,
△OGF面积为,
扇形COF面积为
∴阴影部分面积=矩形OCEG面积-△OGF面积-扇形COF面积=.
【点睛】本题为圆的综合题,考查了切线的判定,垂径定理,扇形的面积等知识,综合性较强,熟练掌握相关定理并根据题意添加辅助线是解题的关键.
25.(2021·湖南株洲·中考真题)如图所示,是的直径,点、是上不同的两点,直线交线段于点,交过点的直线于点,若,且.
(1)求证:直线是的切线;
(2)连接、、、,若.
①求证:;
②过点作,交线段于点,点为线段的中点,若,求线段的长度.
【答案】(1)证明见解析;(2)①证明见解析;②1
【分析】
(1)先将转化为,再利用勾股定理逆定理证明即可;
(2)①利用同一条弧所对的圆周角等于其所对圆心角的一半和同一条弧所对的圆周角相等分别得到与,再利用两角分别相等的两三角形相似即可完成求证;
②分别利用相似三角形的性质和平行线分线段成比例定理的推论求出AC的长和CG的长,最后利用线段的和差关系求解即可.
【详解】解:(1)证:因为,且,
∴,
∴,
∴,
∴直线是的切线;
(2)①∵,
又∵,
∴,
∵,
∴.;
②∵,
∴,
设圆的半径为r,
∵, ,
∴,
∴;
∵点为线段的中点,
∴,
∵,
∴,
∴,
∴,
∴线段的长度为1.
【点睛】本题综合考查了切线的判定定理、圆周角定理及其推论、勾股定理逆定理、相似三角形的判定与性质、平行线分线段成比例定理的推论等内容,解决本题的关键是牢记相关概念,能根据题意建立相等关系等,本题考查内容较多,综合性较强,对学生的综合分析能力有较高要求.
同课章节目录
