沪科版数学八年级下册第18章勾股定理单元检测题(含答案)
文档属性
| 名称 | 沪科版数学八年级下册第18章勾股定理单元检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 488.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 17:10:55 | ||
图片预览


文档简介
第18章《勾股定理》单元检测题 八年级下册数学沪科版
一、单选题(共10小题,满分40分)
1.明明在玩摆木棒游戏,帮他看一看哪一组长度的木棒可以构成直角三角形( )
A.2,3,4 B.3,4,6 C.6,7,11 D.5,12,13
2.从2023年12月开始,哈尔滨因花式宠粉南方游客频繁登上热搜.元旦假期,哈尔滨接棒淄博,成为这个冬天最火爆的旅游城市.为了防止游客脚滑,工作人员在哈尔滨中央大街地下通道铺设防滑地毯.如图是地下通道部分阶梯的示意图,阶梯的宽为,,,若在阶梯上铺设防滑材料,则所需防滑材料的面积至少为( )
A. B. C. D.
3.如图,点A,B,C表示某旅游景区三个缆车车站的位置,线段AB,BC表示连接缆车车站的钢缆,已知A,B,C三点在同一平面内,它们的海拔高度,,分别为110米,310米,710米,BD⊥,AE⊥,垂足分别为D,E,AE与相交于点F,且AF=2BF,CD=BD,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度为( )
A.1000米 B.1200米 C.1400米 D.1500米
4.下列各组的三个数据分别是三角形三边的长度,能判断是等腰直角三角形的一组是( )
A.1,2,3 B.1,1, C.1,1, D.1,2,
5.在中,,,,则的长是( )
A. B. C. D.
6.下列各比值中,是直角三角形的三边之比的是( )
A. B. C. D.3:4:5
7.在Rt△ABC中,以两直角边为边长的正方形面积如图所示,则AB的长为( )
A.49 B. C.3 D.7
8.有下列说法:①有理数与数轴上的点一一对应;②直角三角形的两边长是5和12,则第三边
长是13;③近似数1.5万精确到十分位;④无理数是无限小数.其中错误说法的个数有( )
A.4个 B.3个 C.2个 D.1个
9.三角形分别满足下列条件:
(1)一个内角等于另外两个内角之和;
(2)三边分别为1,,;
(3)三个内角之比为3:4:5;
(4)一边上的中线等于这条边的一半;
其中直角三角形有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在中,,于点,平分,且于点,与相交于点,是边的中点,连接、与相交于点,下列结论:
①是等腰三角形;②;③是的垂直平分线;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题,满分32分)
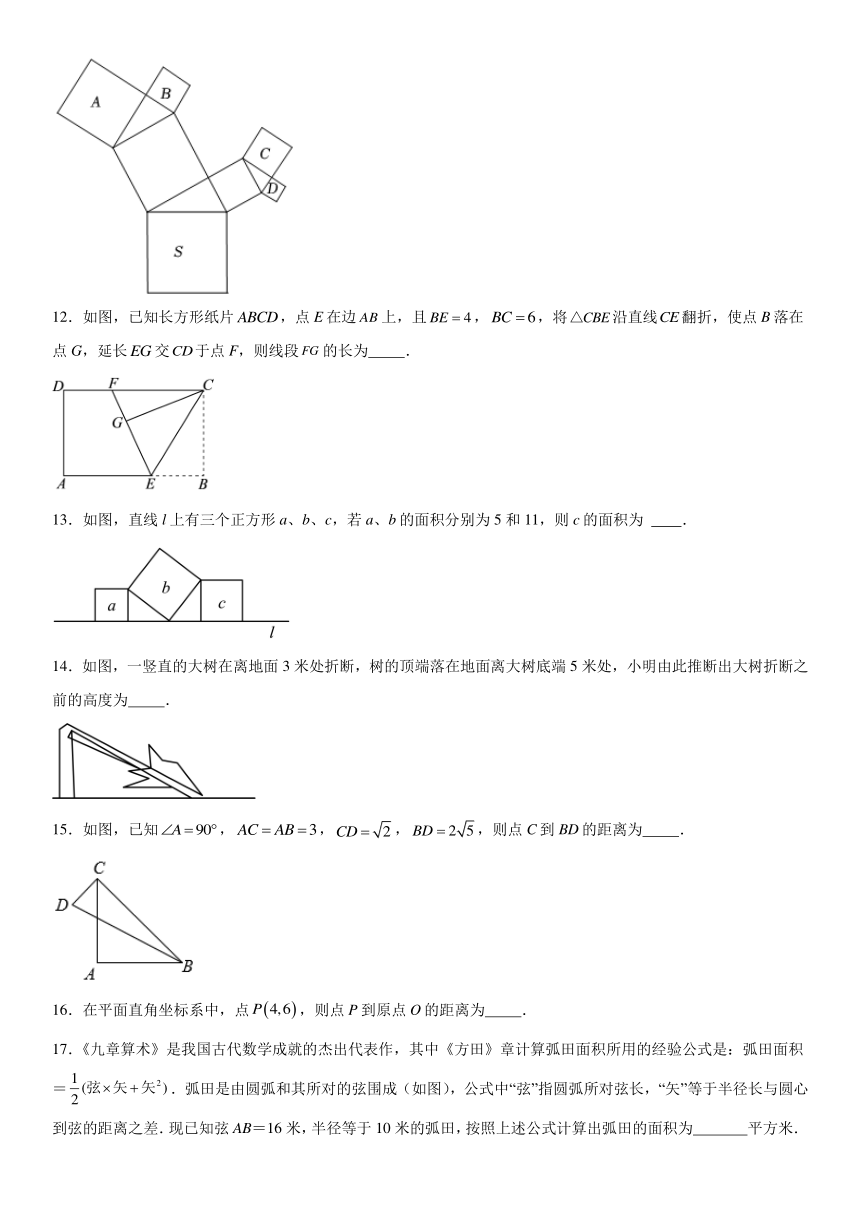
11.如图,所有的四边形都是正方形.所有的三角形都是直角三角形,其中,,,,则 .
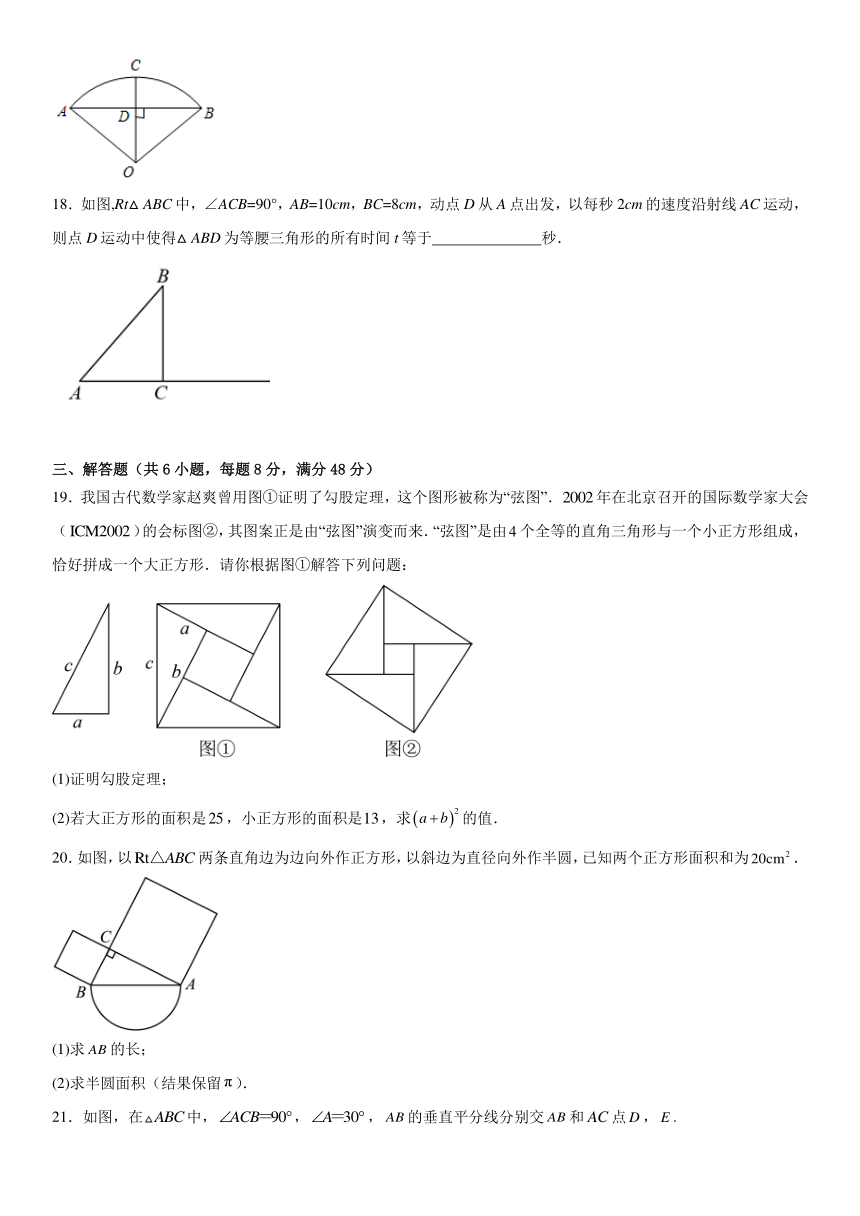
12.如图,已知长方形纸片,点E在边上,且,,将沿直线翻折,使点B落在点G,延长交于点F,则线段的长为 .
13.如图,直线l上有三个正方形a、b、c,若a、b的面积分别为5和11,则c的面积为 .
14.如图,一竖直的大树在离地面3米处折断,树的顶端落在地面离大树底端5米处,小明由此推断出大树折断之前的高度为 .
15.如图,已知,,,,则点C到BD的距离为 .
16.在平面直角坐标系中,点,则点P到原点O的距离为 .
17.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=.弧田是由圆弧和其所对的弦围成(如图),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.现已知弦AB=16米,半径等于10米的弧田,按照上述公式计算出弧田的面积为 平方米.
18.如图,Rt△ABC中,∠ACB=90°,AB=10cm,BC=8cm,动点D从A点出发,以每秒2cm的速度沿射线AC运动,则点D运动中使得△ABD为等腰三角形的所有时间t等于 秒.
三、解答题(共6小题,每题8分,满分48分)
19.我国古代数学家赵爽曾用图①证明了勾股定理,这个图形被称为“弦图”.年在北京召开的国际数学家大会()的会标图②,其图案正是由“弦图”演变而来.“弦图”是由个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.请你根据图①解答下列问题:
(1)证明勾股定理;
(2)若大正方形的面积是,小正方形的面积是,求的值.
20.如图,以两条直角边为边向外作正方形,以斜边为直径向外作半圆,已知两个正方形面积和为.
(1)求的长;
(2)求半圆面积(结果保留).
21.如图,在中,,,的垂直平分线分别交和点,.
(1)求证:
(2)若,求的长.
22.数学中,常对同一个量(图形的面积、点的个数等)用两种不同的方法计算,从而建立相等关系,我们把这种思想叫“算两次”.“算两次”也称作富比尼原理,是一种重要的数学思想,由它可以推导出很多重要的公式.
(1)如图1,是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形.
①用“算两次”的方法计算图2中阴影部分的面积:第一次列式为 ,第二次列式为 ,因为两次所列算式表示的是同一个图形的面积,所以可以得出等式 ;
②在①中,如果,,请直接用①题中的等式,求阴影部分的面积;
(2)如图3,两个边长分别为,,的直角三角形和一个两条直角边都是的直角三角形拼成一个梯形,用“算两次”的方法,探究,,之间的数量关系.
23.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)面出格点(顶点均在格点上)关于直线l对称的;
(2)在l上画出点P,使最小,这个最短长度的平方是______.
24.如图1,在平面直角坐标系中,点O为坐标原点,直线y=kx﹣1交x轴正半轴于点A,交y轴负半轴于点B,AB=.
(1)求k的值;
(2)如图2,P为y轴正半轴上一点,过点P作PD⊥AB于点D,交线段OA于点E,设点P的纵坐标为t,线段AD的长d,求d与t的函数解析式;
(3)如图3,在(2)的条件下,d=,点H在线段OP上,连接AH,AH=HP,点G为第一象限内直线AP上方一点,连接PG、AG,∠APG=30°,点F为第二象限内一点,连接OF、FH、FG,若FG=AG,∠AHO+2∠OHF=180°,∠APG+∠AGF=2∠FOH,∠AGF﹣∠FOH=15°,求点F的坐标.
参考答案:
1.D
2.A
3.A
4.B
5.D
6.D
7.D
8.B
9.C
10.D
11.31
12.//
13.
14.米
15./
16.
17.40
18.5或6或
19.(1)11
(2)
20.(1)
(2)
21.(1)证明略;(2)BC=2.
22.(1)①,,;或,,;②9;(2)
23.(1)略
(2)32
24.(1)k=;(2)d=(0<t≤9);(3)F(﹣1,1).
一、单选题(共10小题,满分40分)
1.明明在玩摆木棒游戏,帮他看一看哪一组长度的木棒可以构成直角三角形( )
A.2,3,4 B.3,4,6 C.6,7,11 D.5,12,13
2.从2023年12月开始,哈尔滨因花式宠粉南方游客频繁登上热搜.元旦假期,哈尔滨接棒淄博,成为这个冬天最火爆的旅游城市.为了防止游客脚滑,工作人员在哈尔滨中央大街地下通道铺设防滑地毯.如图是地下通道部分阶梯的示意图,阶梯的宽为,,,若在阶梯上铺设防滑材料,则所需防滑材料的面积至少为( )
A. B. C. D.
3.如图,点A,B,C表示某旅游景区三个缆车车站的位置,线段AB,BC表示连接缆车车站的钢缆,已知A,B,C三点在同一平面内,它们的海拔高度,,分别为110米,310米,710米,BD⊥,AE⊥,垂足分别为D,E,AE与相交于点F,且AF=2BF,CD=BD,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度为( )
A.1000米 B.1200米 C.1400米 D.1500米
4.下列各组的三个数据分别是三角形三边的长度,能判断是等腰直角三角形的一组是( )
A.1,2,3 B.1,1, C.1,1, D.1,2,
5.在中,,,,则的长是( )
A. B. C. D.
6.下列各比值中,是直角三角形的三边之比的是( )
A. B. C. D.3:4:5
7.在Rt△ABC中,以两直角边为边长的正方形面积如图所示,则AB的长为( )
A.49 B. C.3 D.7
8.有下列说法:①有理数与数轴上的点一一对应;②直角三角形的两边长是5和12,则第三边
长是13;③近似数1.5万精确到十分位;④无理数是无限小数.其中错误说法的个数有( )
A.4个 B.3个 C.2个 D.1个
9.三角形分别满足下列条件:
(1)一个内角等于另外两个内角之和;
(2)三边分别为1,,;
(3)三个内角之比为3:4:5;
(4)一边上的中线等于这条边的一半;
其中直角三角形有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在中,,于点,平分,且于点,与相交于点,是边的中点,连接、与相交于点,下列结论:
①是等腰三角形;②;③是的垂直平分线;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题,满分32分)
11.如图,所有的四边形都是正方形.所有的三角形都是直角三角形,其中,,,,则 .
12.如图,已知长方形纸片,点E在边上,且,,将沿直线翻折,使点B落在点G,延长交于点F,则线段的长为 .
13.如图,直线l上有三个正方形a、b、c,若a、b的面积分别为5和11,则c的面积为 .
14.如图,一竖直的大树在离地面3米处折断,树的顶端落在地面离大树底端5米处,小明由此推断出大树折断之前的高度为 .
15.如图,已知,,,,则点C到BD的距离为 .
16.在平面直角坐标系中,点,则点P到原点O的距离为 .
17.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=.弧田是由圆弧和其所对的弦围成(如图),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.现已知弦AB=16米,半径等于10米的弧田,按照上述公式计算出弧田的面积为 平方米.
18.如图,Rt△ABC中,∠ACB=90°,AB=10cm,BC=8cm,动点D从A点出发,以每秒2cm的速度沿射线AC运动,则点D运动中使得△ABD为等腰三角形的所有时间t等于 秒.
三、解答题(共6小题,每题8分,满分48分)
19.我国古代数学家赵爽曾用图①证明了勾股定理,这个图形被称为“弦图”.年在北京召开的国际数学家大会()的会标图②,其图案正是由“弦图”演变而来.“弦图”是由个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.请你根据图①解答下列问题:
(1)证明勾股定理;
(2)若大正方形的面积是,小正方形的面积是,求的值.
20.如图,以两条直角边为边向外作正方形,以斜边为直径向外作半圆,已知两个正方形面积和为.
(1)求的长;
(2)求半圆面积(结果保留).
21.如图,在中,,,的垂直平分线分别交和点,.
(1)求证:
(2)若,求的长.
22.数学中,常对同一个量(图形的面积、点的个数等)用两种不同的方法计算,从而建立相等关系,我们把这种思想叫“算两次”.“算两次”也称作富比尼原理,是一种重要的数学思想,由它可以推导出很多重要的公式.
(1)如图1,是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形.
①用“算两次”的方法计算图2中阴影部分的面积:第一次列式为 ,第二次列式为 ,因为两次所列算式表示的是同一个图形的面积,所以可以得出等式 ;
②在①中,如果,,请直接用①题中的等式,求阴影部分的面积;
(2)如图3,两个边长分别为,,的直角三角形和一个两条直角边都是的直角三角形拼成一个梯形,用“算两次”的方法,探究,,之间的数量关系.
23.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)面出格点(顶点均在格点上)关于直线l对称的;
(2)在l上画出点P,使最小,这个最短长度的平方是______.
24.如图1,在平面直角坐标系中,点O为坐标原点,直线y=kx﹣1交x轴正半轴于点A,交y轴负半轴于点B,AB=.
(1)求k的值;
(2)如图2,P为y轴正半轴上一点,过点P作PD⊥AB于点D,交线段OA于点E,设点P的纵坐标为t,线段AD的长d,求d与t的函数解析式;
(3)如图3,在(2)的条件下,d=,点H在线段OP上,连接AH,AH=HP,点G为第一象限内直线AP上方一点,连接PG、AG,∠APG=30°,点F为第二象限内一点,连接OF、FH、FG,若FG=AG,∠AHO+2∠OHF=180°,∠APG+∠AGF=2∠FOH,∠AGF﹣∠FOH=15°,求点F的坐标.
参考答案:
1.D
2.A
3.A
4.B
5.D
6.D
7.D
8.B
9.C
10.D
11.31
12.//
13.
14.米
15./
16.
17.40
18.5或6或
19.(1)11
(2)
20.(1)
(2)
21.(1)证明略;(2)BC=2.
22.(1)①,,;或,,;②9;(2)
23.(1)略
(2)32
24.(1)k=;(2)d=(0<t≤9);(3)F(﹣1,1).
