18.2 特殊的平行四边形 同步练习(含答案)人教版数学八年级下册
文档属性
| 名称 | 18.2 特殊的平行四边形 同步练习(含答案)人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 258.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览

文档简介
18.2 特殊的平行四边形 同步练习
一、单选题
1.下面的性质中,平行四边形、矩形、菱形、正方形都具有的是( )
A.四边相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
2.若菱形的较长对角线为24cm,面积为120cm2,则它的周长为( )
A.50cm B.51cm C.52cm D.56cm
3.如图,把一张长方形的纸沿对角线BD折叠,使点C落到点的位置,若平分,则的度数是( )
A.15° B.30° C.45° D.60°
4.如图,点P是菱形对角线上一点,于点E,且.连接,若菱形的周长为24.则的面积为()
A.4 B.6 C.8 D.12
5.如图,在正方形的外侧,作等边三角形,则为( )
A.45° B.25° C.30° D.40°
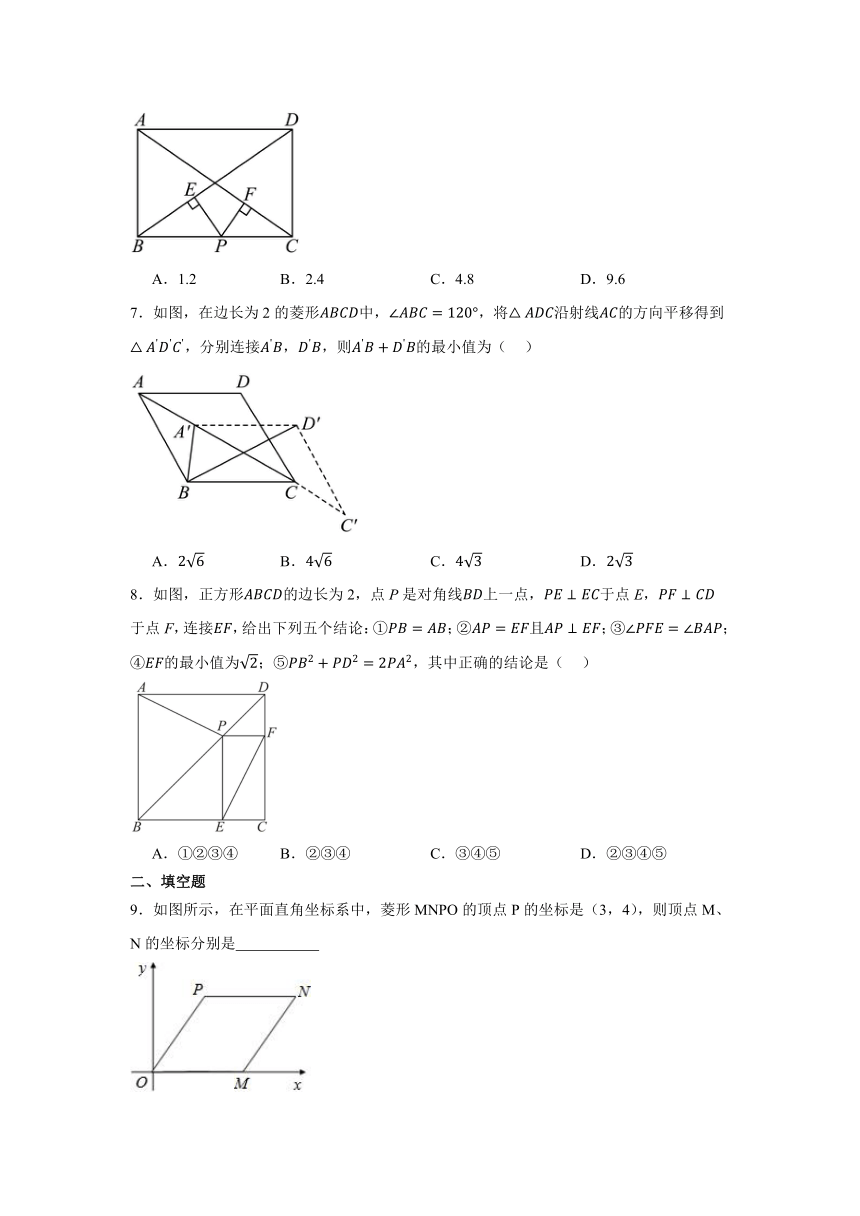
6.如图,矩形中,是上的点,于于,则( )
A.1.2 B.2.4 C.4.8 D.9.6
7.如图,在边长为2的菱形中,,将沿射线的方向平移得到,分别连接,,则的最小值为( )
A. B. C. D.
8.如图,正方形的边长为2,点P是对角线上一点,于点E,于点F,连接,给出下列五个结论:①;②且;③;④的最小值为;⑤,其中正确的结论是( )
A.①②③④ B.②③④ C.③④⑤ D.②③④⑤
二、填空题
9.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是
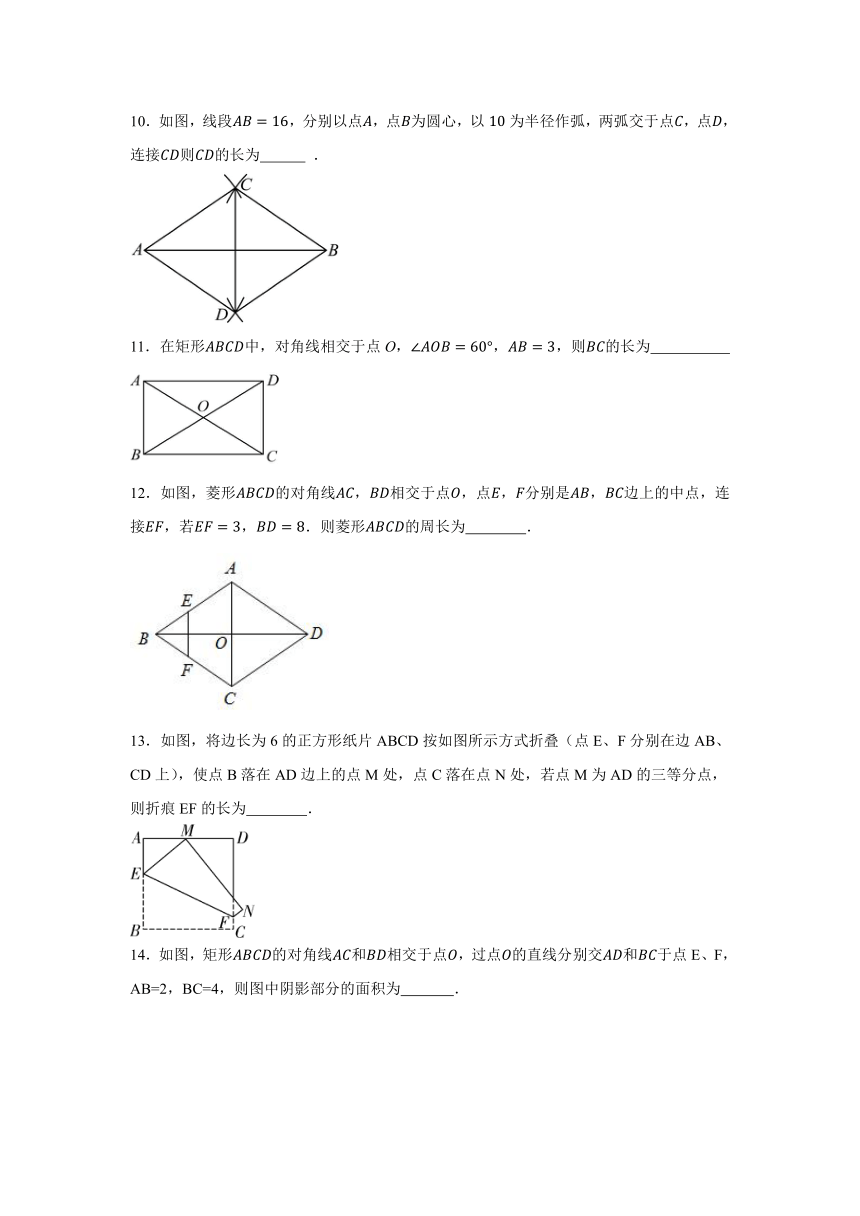
10.如图,线段,分别以点,点为圆心,以为半径作弧,两弧交于点,点,连接则的长为 .
11.在矩形中,对角线相交于点O,,,则的长为
12.如图,菱形的对角线,相交于点,点,分别是,边上的中点,连接,若,.则菱形的周长为 .
13.如图,将边长为6的正方形纸片ABCD按如图所示方式折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若点M为AD的三等分点,则折痕EF的长为 .
14.如图,矩形的对角线和相交于点,过点的直线分别交和于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
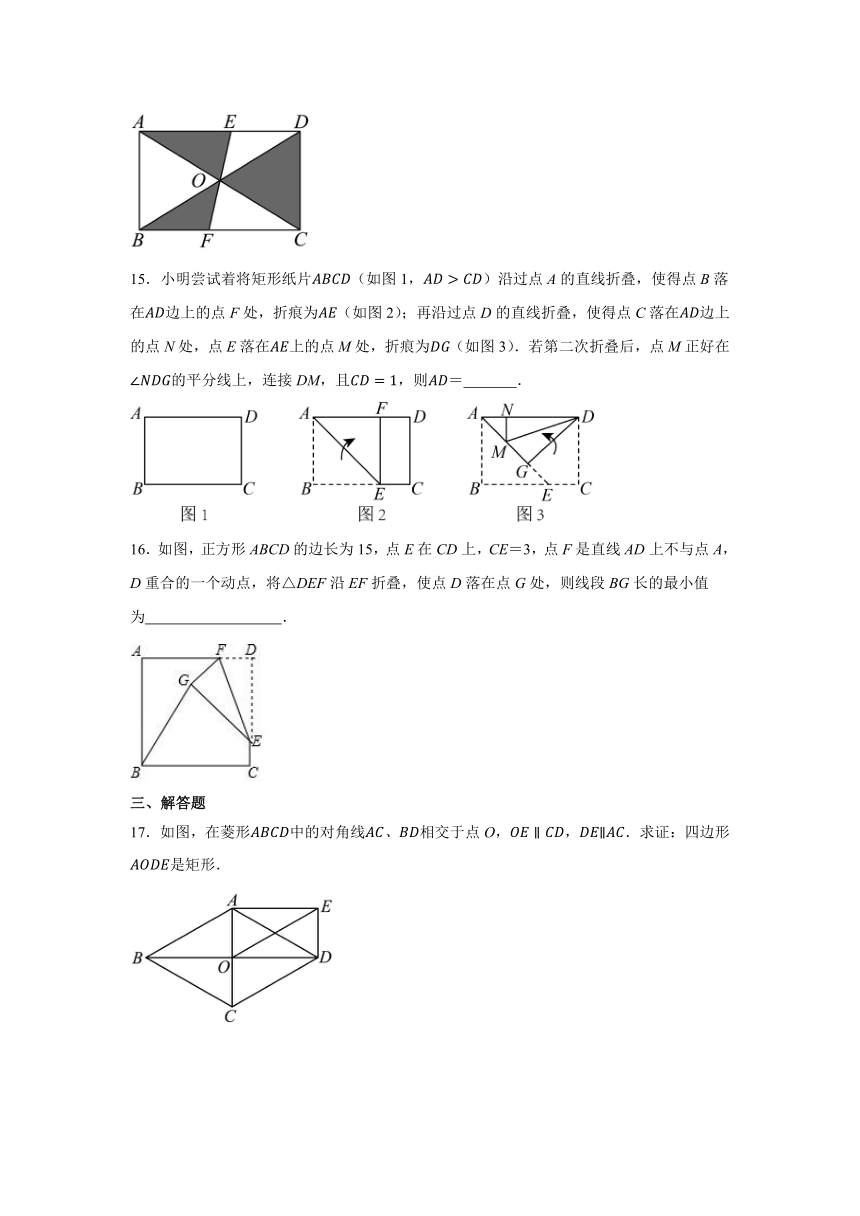
15.小明尝试着将矩形纸片(如图1,)沿过点A的直线折叠,使得点B落在边上的点F处,折痕为(如图2);再沿过点D的直线折叠,使得点C落在边上的点N处,点E落在上的点M处,折痕为(如图3).若第二次折叠后,点M正好在的平分线上,连接DM,且,则= .
16.如图,正方形ABCD的边长为15,点E在CD上,CE=3,点F是直线AD上不与点A,D重合的一个动点,将△DEF沿EF折叠,使点D落在点G处,则线段BG长的最小值为 .
三、解答题
17.如图,在菱形中的对角线相交于点O,,.求证:四边形是矩形.
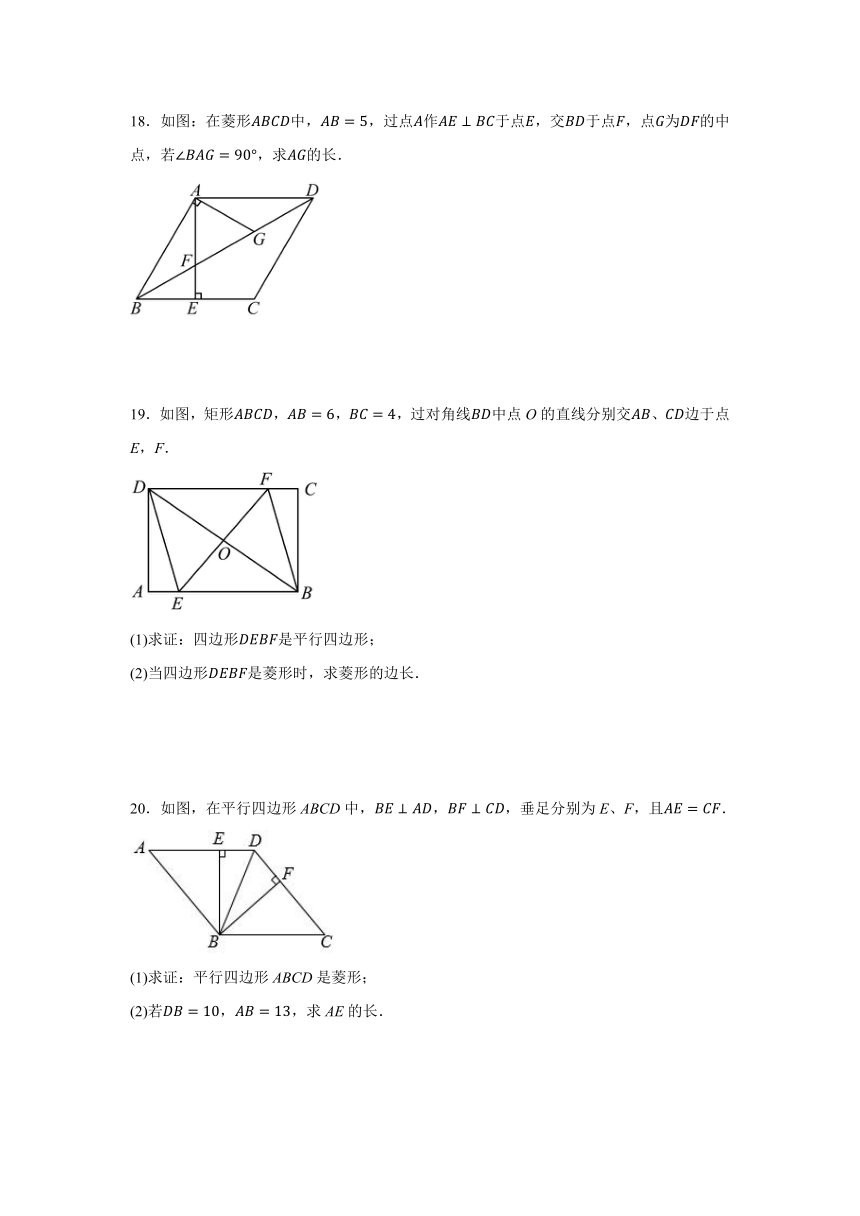
18.如图:在菱形中,,过点作于点,交于点,点为的中点,若,求的长.
19.如图,矩形,,,过对角线中点O的直线分别交、边于点E,F.
(1)求证:四边形是平行四边形;
(2)当四边形是菱形时,求菱形的边长.
20.如图,在平行四边形ABCD中,,,垂足分别为E、F,且.
(1)求证:平行四边形ABCD是菱形;
(2)若,,求AE的长.
21.如图,P是边长为4的正方形ABCD对角线AC上一点(P与A、C不重合),点E在线段BC上,且PE=PB.
(1)若AP=1,求CE的长;
(2)求证:PE⊥PD.
22.已知菱形ABCD中,点P在CD上,连接AP.
(1)在BC上取点Q,使得∠PAQ=∠B,
①图1,当AP⊥CD于点P时,线段AP与AQ之间的数量关系是 .
②如图2,当AP与CD不垂直时,判断①中的结论是否仍然成立,若成立,请给出证明,若不成立,则需说明理由.
(2)在CD的延长线取点N,使得∠PAN=∠B,若AB=4,∠B=60°,∠ANC=45°请依题意画出图形并求此时线段DN的长.
参考答案
1.D
2.C
3.B
4.B
5.A
6.C
7.D
8.D
9.M(5,0),N(8,4)
10.
11.
12.20
13.或
14.4
15.
16.3﹣12
17.证明:∵四边形为菱形,
∴,,
∴,
∵,,
∴四边形为平行四边形,
∴,
∴,
∴四边形是平行四边形,
∴平行四边形是矩形.
18.解:四边形为菱形,
∴,,
,
,
,
,
点为的中点,
,
,
,
,
,
,
,
19.(1)证明:∵四边形是矩形,O是的中点,
∴,,,,
∴,
又∵,
∴,
∴,
又∵,
∴四边形是平行四边形;
(2)当四边形是菱形时,,
设,则,,
在中,,
∴,
解得:,
∴即菱形的边长为.
20.(1)∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠AEB=∠CFB=90°,
在△ABE和△CBF中,
∴△ABE≌△CBF(ASA),
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴AD=AB=13,
设AE=x,则DE=13﹣x,
在Rt△ABE和Rt△BDE中,由勾股定理得:BE2=AB2﹣AE2=DB2﹣DE2,
即132﹣x2=102﹣(13﹣x)2,
解得:.
即AE=.
21.(1)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
∵△AGP和△PFC都是等腰直角三角形.
∴GP=AG=BF,GD=FC=FP
又∵AP=1,AD=4,
∴GP=AG=BF=,GD=FC=FP=4 ,
又∵PB=PE,PF⊥BE
∴BF=FE=,
∴CE=BC-BF-EF=4-2×=4-
(2)由(1)得:
在△EFP和△PGD中
∴△PGD≌△EFP(SAS),
∴∠1=∠2.
∴∠1+∠3=∠2+∠3=90°.
∴∠DPE=90°.
∴PE⊥PD.
22.(1)解:①AP=AQ.
∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,
∴∠B+∠QCD=180°,
∵∠PAQ=∠B,
∴∠PAQ+∠QCD=180°,
∴∠APC+∠AQC=180°,
∵AP⊥CD,
∴∠APC=90°,
∴∠AQC=90°,
∴AQ⊥BC,
∵S菱形ABCD=BC AQ=CD AP,
∴AP=AQ;
故答案为:AP=AQ;
②答:①中的结论仍然成立.
证明:如图2中,过点A作AM⊥BC于M,AN⊥CD于N.
∵四边形ABCD是菱形,AM⊥BC,AN⊥CD,
∴S菱形ABCD=BC AM=CD AN,
∵BC=CD,
∴AM=AN,∠AMQ=∠ANP=90°,AB∥CD,
∴∠B+∠C=180°,
∵∠PAQ=∠B,
∴∠PAQ+∠C=180°,
∴∠AQC+∠APC=180°,
∵∠AQM+∠AQC=180°,
∴∠AQM=∠APN,
在△AMQ和△ANP中,
∴△AMQ≌△ANP(AAS),
∴AP=AQ.
(2)解:作∠PAN=∠B,角的另一边交CD延长于N,
如图3,过点A作AH⊥CD于点H,
∵∠ANC=45°,
∴∠NAH=45°,
∴AH=HN,
∵四边形ABCD是菱形,∠B=60°,
∴∠ADC=60°,AB=AD=4,
∴∠DAH=90°-∠ADH=90°-60°=30°,
∴DH=AD=2,
∴AH==DH=2,
∴HN=2,
∴DN=HN﹣DH=2﹣2.
一、单选题
1.下面的性质中,平行四边形、矩形、菱形、正方形都具有的是( )
A.四边相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
2.若菱形的较长对角线为24cm,面积为120cm2,则它的周长为( )
A.50cm B.51cm C.52cm D.56cm
3.如图,把一张长方形的纸沿对角线BD折叠,使点C落到点的位置,若平分,则的度数是( )
A.15° B.30° C.45° D.60°
4.如图,点P是菱形对角线上一点,于点E,且.连接,若菱形的周长为24.则的面积为()
A.4 B.6 C.8 D.12
5.如图,在正方形的外侧,作等边三角形,则为( )
A.45° B.25° C.30° D.40°
6.如图,矩形中,是上的点,于于,则( )
A.1.2 B.2.4 C.4.8 D.9.6
7.如图,在边长为2的菱形中,,将沿射线的方向平移得到,分别连接,,则的最小值为( )
A. B. C. D.
8.如图,正方形的边长为2,点P是对角线上一点,于点E,于点F,连接,给出下列五个结论:①;②且;③;④的最小值为;⑤,其中正确的结论是( )
A.①②③④ B.②③④ C.③④⑤ D.②③④⑤
二、填空题
9.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是
10.如图,线段,分别以点,点为圆心,以为半径作弧,两弧交于点,点,连接则的长为 .
11.在矩形中,对角线相交于点O,,,则的长为
12.如图,菱形的对角线,相交于点,点,分别是,边上的中点,连接,若,.则菱形的周长为 .
13.如图,将边长为6的正方形纸片ABCD按如图所示方式折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若点M为AD的三等分点,则折痕EF的长为 .
14.如图,矩形的对角线和相交于点,过点的直线分别交和于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
15.小明尝试着将矩形纸片(如图1,)沿过点A的直线折叠,使得点B落在边上的点F处,折痕为(如图2);再沿过点D的直线折叠,使得点C落在边上的点N处,点E落在上的点M处,折痕为(如图3).若第二次折叠后,点M正好在的平分线上,连接DM,且,则= .
16.如图,正方形ABCD的边长为15,点E在CD上,CE=3,点F是直线AD上不与点A,D重合的一个动点,将△DEF沿EF折叠,使点D落在点G处,则线段BG长的最小值为 .
三、解答题
17.如图,在菱形中的对角线相交于点O,,.求证:四边形是矩形.
18.如图:在菱形中,,过点作于点,交于点,点为的中点,若,求的长.
19.如图,矩形,,,过对角线中点O的直线分别交、边于点E,F.
(1)求证:四边形是平行四边形;
(2)当四边形是菱形时,求菱形的边长.
20.如图,在平行四边形ABCD中,,,垂足分别为E、F,且.
(1)求证:平行四边形ABCD是菱形;
(2)若,,求AE的长.
21.如图,P是边长为4的正方形ABCD对角线AC上一点(P与A、C不重合),点E在线段BC上,且PE=PB.
(1)若AP=1,求CE的长;
(2)求证:PE⊥PD.
22.已知菱形ABCD中,点P在CD上,连接AP.
(1)在BC上取点Q,使得∠PAQ=∠B,
①图1,当AP⊥CD于点P时,线段AP与AQ之间的数量关系是 .
②如图2,当AP与CD不垂直时,判断①中的结论是否仍然成立,若成立,请给出证明,若不成立,则需说明理由.
(2)在CD的延长线取点N,使得∠PAN=∠B,若AB=4,∠B=60°,∠ANC=45°请依题意画出图形并求此时线段DN的长.
参考答案
1.D
2.C
3.B
4.B
5.A
6.C
7.D
8.D
9.M(5,0),N(8,4)
10.
11.
12.20
13.或
14.4
15.
16.3﹣12
17.证明:∵四边形为菱形,
∴,,
∴,
∵,,
∴四边形为平行四边形,
∴,
∴,
∴四边形是平行四边形,
∴平行四边形是矩形.
18.解:四边形为菱形,
∴,,
,
,
,
,
点为的中点,
,
,
,
,
,
,
,
19.(1)证明:∵四边形是矩形,O是的中点,
∴,,,,
∴,
又∵,
∴,
∴,
又∵,
∴四边形是平行四边形;
(2)当四边形是菱形时,,
设,则,,
在中,,
∴,
解得:,
∴即菱形的边长为.
20.(1)∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠AEB=∠CFB=90°,
在△ABE和△CBF中,
∴△ABE≌△CBF(ASA),
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴AD=AB=13,
设AE=x,则DE=13﹣x,
在Rt△ABE和Rt△BDE中,由勾股定理得:BE2=AB2﹣AE2=DB2﹣DE2,
即132﹣x2=102﹣(13﹣x)2,
解得:.
即AE=.
21.(1)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
∵△AGP和△PFC都是等腰直角三角形.
∴GP=AG=BF,GD=FC=FP
又∵AP=1,AD=4,
∴GP=AG=BF=,GD=FC=FP=4 ,
又∵PB=PE,PF⊥BE
∴BF=FE=,
∴CE=BC-BF-EF=4-2×=4-
(2)由(1)得:
在△EFP和△PGD中
∴△PGD≌△EFP(SAS),
∴∠1=∠2.
∴∠1+∠3=∠2+∠3=90°.
∴∠DPE=90°.
∴PE⊥PD.
22.(1)解:①AP=AQ.
∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,
∴∠B+∠QCD=180°,
∵∠PAQ=∠B,
∴∠PAQ+∠QCD=180°,
∴∠APC+∠AQC=180°,
∵AP⊥CD,
∴∠APC=90°,
∴∠AQC=90°,
∴AQ⊥BC,
∵S菱形ABCD=BC AQ=CD AP,
∴AP=AQ;
故答案为:AP=AQ;
②答:①中的结论仍然成立.
证明:如图2中,过点A作AM⊥BC于M,AN⊥CD于N.
∵四边形ABCD是菱形,AM⊥BC,AN⊥CD,
∴S菱形ABCD=BC AM=CD AN,
∵BC=CD,
∴AM=AN,∠AMQ=∠ANP=90°,AB∥CD,
∴∠B+∠C=180°,
∵∠PAQ=∠B,
∴∠PAQ+∠C=180°,
∴∠AQC+∠APC=180°,
∵∠AQM+∠AQC=180°,
∴∠AQM=∠APN,
在△AMQ和△ANP中,
∴△AMQ≌△ANP(AAS),
∴AP=AQ.
(2)解:作∠PAN=∠B,角的另一边交CD延长于N,
如图3,过点A作AH⊥CD于点H,
∵∠ANC=45°,
∴∠NAH=45°,
∴AH=HN,
∵四边形ABCD是菱形,∠B=60°,
∴∠ADC=60°,AB=AD=4,
∴∠DAH=90°-∠ADH=90°-60°=30°,
∴DH=AD=2,
∴AH==DH=2,
∴HN=2,
∴DN=HN﹣DH=2﹣2.
