4.3 探索三角形全等的条件 同步基础达标练习题(含答案)北师大版数学七年级下册
文档属性
| 名称 | 4.3 探索三角形全等的条件 同步基础达标练习题(含答案)北师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 338.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览



文档简介
北师大版七年级数学下册《4.3探索三角形全等的条件》
同步基础达标练习题
一、单选题
1.下列图形具有稳定性的是( )
A.锐角三角形 B.正方形 C.五边形 D.六边形
2.如图,中,,,直接使用“”可判定( )
A. B.
C. D.
3.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A. B. C. D.
4.如图,已知,若用“”证明,还需添加条件( )
A. B. C. D.
5.如图,OA=OB,OC=OD,∠O=50°,∠D=30°,则∠AEC等于( )
A.70° B.50° C.45° D.60°
6.如图,已知,,从①,②,③,④.这四个条件中再选一个使,符合条件的有( )
A.1个 B.2个 C.3个 D.4个
7.小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带去( )
A.第1块 B.第2块 C.第3块 D.第4块
8.如图,在中,,,过点C作,且,则的面积为( )
A.4 B.6 C.7 D.8
二、填空题
9.如图,已知,,请再添加一个条件,使得.这个条件可以是: .(只填一个条件即可)
10.如图,要测量池塘的宽度,在池塘外选取一点,连接并各自延长,使,连接,测得长为,则池塘宽为,依据是 .
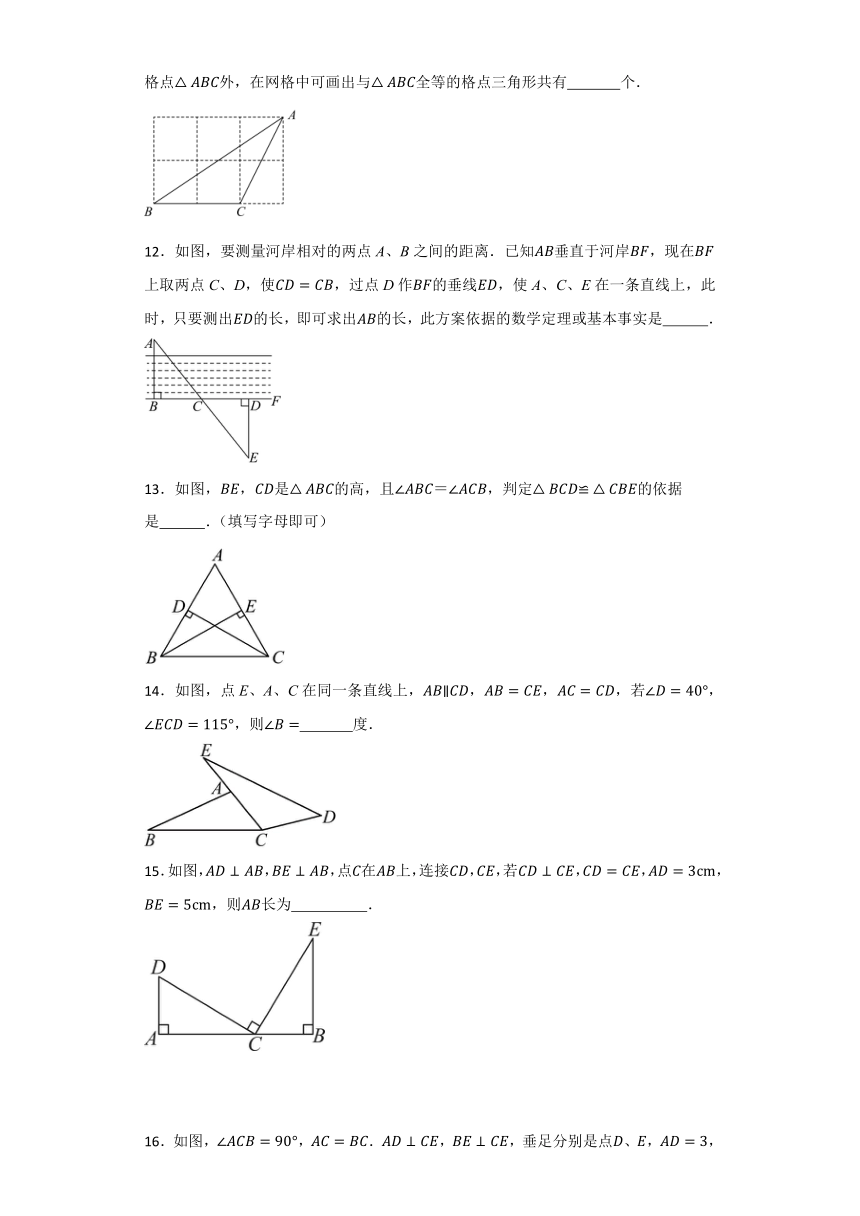
11.如图,的3个顶点分别在小正方形的顶点(格点)上的三角形叫格点三角形.除格点外,在网格中可画出与全等的格点三角形共有 个.
12.如图,要测量河岸相对的两点A、B之间的距离.已知垂直于河岸,现在上取两点C、D,使,过点D作的垂线,使A、C、E在一条直线上,此时,只要测出的长,即可求出的长,此方案依据的数学定理或基本事实是 .
13.如图,,是的高,且,判定的依据是 .(填写字母即可)
14.如图,点E、A、C在同一条直线上,,,,若,,则 度.
15.如图,,,点在上,连接,,若,,,,则长为 .
16.如图,,.,,垂足分别是点、,,,则的长是 .
三、解答题
17.把下面的说理过程补充完整:
已知:如图,,,,线段和线段平行吗?请说明理由.
答:,理由:
∵(已知)
∴______(等式的性质)
∴______
∵(已知)
∴ (两直线平行,内错角相等)
又∵(已知)
∴( )
∴ (全等三角形的对应角相等)
∴(内错角相等,两直线平行)
18.如图,在和中,,,且,点在上.过点作,连接.求证:;
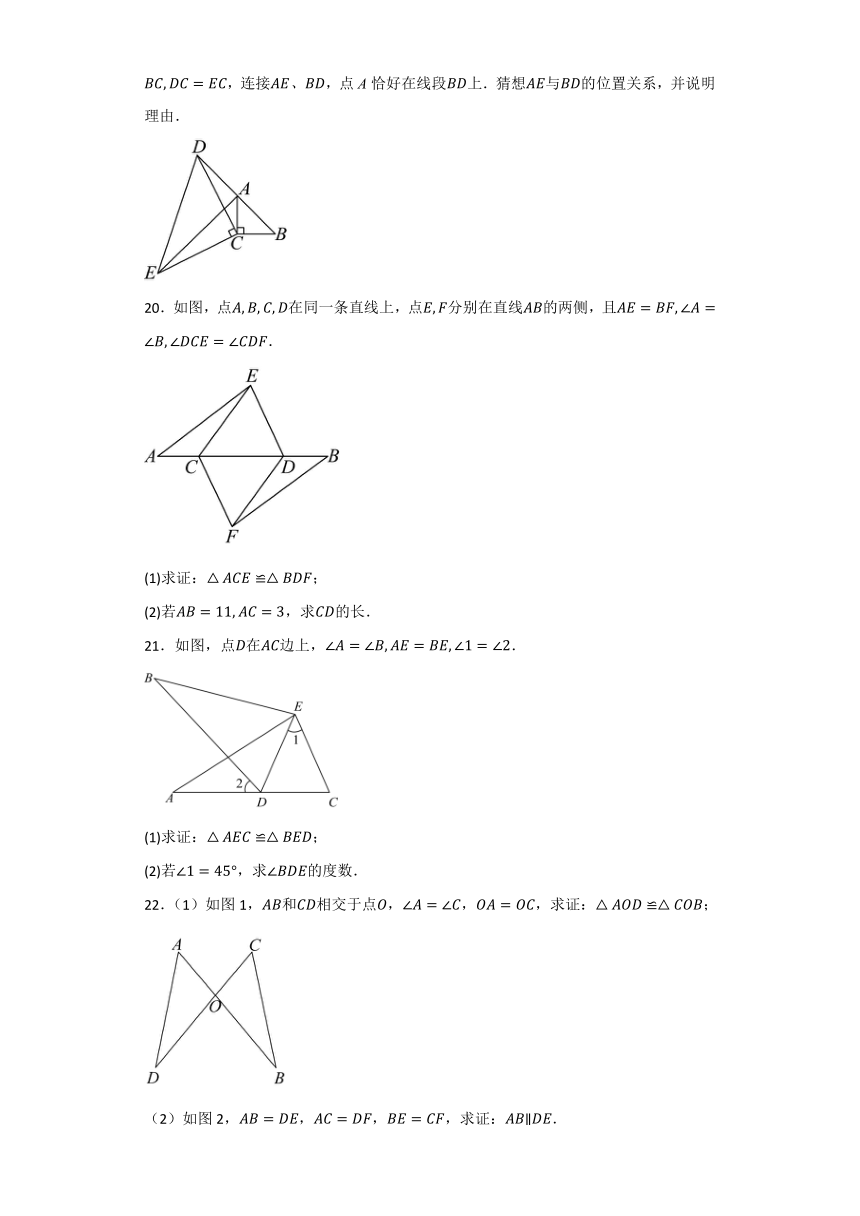
19.如图,大小不同的两块三角板和直角顶点重合在点处,,连接,点A恰好在线段上.猜想与的位置关系,并说明理由.
20.如图,点在同一条直线上,点分别在直线的两侧,且.
(1)求证:;
(2)若,求的长.
21.如图,点在边上,.
(1)求证:;
(2)若,求的度数.
22.(1)如图1,和相交于点,,,求证:;
(2)如图2,,,,求证:.
参考答案
1.解:根据三角形的稳定性,可知:
、具有稳定性,符合题意,
、不具有稳定性,不符合题意,
、不具有稳定性,不符合题意,
、不具有稳定性,不符合题意,
故选:.
2.解:∵,,,
∴,
根据现有条件无法直接利用判定,,,
故选:C.
3.解:由作图可知,,,,
.
故答案为:A.
4.解:∵,,
∴补充,不能证明,
补充,由证明,
补充,由可证明,
故选:C.
5.解:∵如图,在△AOD中,∠O=50°,∠D=30°,
∴∠OAD=180°﹣50°﹣30°=100°,
在△AOD与△BOC中,
,
∴△AOD≌△BOC(SAS),
故∠OAD=∠OBC=100°.
在四边形OBEA中,
∠AEB=360°﹣∠OBC﹣∠OAD﹣∠O
=360°﹣100°﹣100°﹣50°
=110°,
又∵∠AEB+∠AEC=180°,
∴∠AEC=180°﹣110°=70°.
故选:A.
6.解:∵,
∴,即,
①∵,,
∴,故①正确;
添加③,
∴,故③正确;
添加④,
∴,故④正确;
添加条件②,不能证明,故②错误;
故选:C.
7.解:由1、2、3块玻璃不同时具备包括一完整边在内的三个证明全等的要素,则不能带它们去,只有第4块有完整的两角及夹边,符合,满足题目要求的条件,符合题意.
故选:D.
8.解:如图,过点作交延长线于点,
∵,,,
∴,,,
∴,
在和中,
,
∴
∴
故选:D
9.解:添加,根据可以判定,
故答案为:.
10.解:在和中,
,
∴,
∴,
故答案为:.
11.解:如图,
图中与全等的格点三角形是,共3个,
故答案为:3
12.解:∵,
∴,
∵
∴
∴
故根据全等三角形的对应边相等,只要测出的长,即可求出的长
故答案为:全等三角形的对应边相等
13.解:∵,是的高,
∴,
在与中,
,
∴,
故答案为:.
14.解:∵,,
∴
∵,
∴
∵,,
∴,
∴
故答案为:
15.解:,
,
,
,
,
,
在和中,
,
,
,,
.
故答案为:.
16.解:,,
,
.
,
.
在和中,
,
,
,.
故选答案为2.
17.解:,理由:
∵(已知)
∴(等式的性质)
∴
∵(已知)
∴(两直线平行,内错角相等)
又∵(已知)
∴()
∴(全等三角形的对应角相等)
∴(内错角相等,两直线平行)
故答案为:,,,.
18.解:∵,
∴,
∴,
在和中
∵,
∴
19.解:,理由如下:
∵
在与中,
.
.
20.(1)证明:,,且,
,
在和中,
,
.
(2)解:,
,
,
,
的长为5.
21.(1)证明:∵,
∴
∵
∴()
(2)解:∵
∴
∴,
∵
∴
∴
22.解:(1)在和中,
∴
(2)∵,
∴,
即:,
在和中,
∴
∴
∴
同步基础达标练习题
一、单选题
1.下列图形具有稳定性的是( )
A.锐角三角形 B.正方形 C.五边形 D.六边形
2.如图,中,,,直接使用“”可判定( )
A. B.
C. D.
3.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A. B. C. D.
4.如图,已知,若用“”证明,还需添加条件( )
A. B. C. D.
5.如图,OA=OB,OC=OD,∠O=50°,∠D=30°,则∠AEC等于( )
A.70° B.50° C.45° D.60°
6.如图,已知,,从①,②,③,④.这四个条件中再选一个使,符合条件的有( )
A.1个 B.2个 C.3个 D.4个
7.小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带去( )
A.第1块 B.第2块 C.第3块 D.第4块
8.如图,在中,,,过点C作,且,则的面积为( )
A.4 B.6 C.7 D.8
二、填空题
9.如图,已知,,请再添加一个条件,使得.这个条件可以是: .(只填一个条件即可)
10.如图,要测量池塘的宽度,在池塘外选取一点,连接并各自延长,使,连接,测得长为,则池塘宽为,依据是 .
11.如图,的3个顶点分别在小正方形的顶点(格点)上的三角形叫格点三角形.除格点外,在网格中可画出与全等的格点三角形共有 个.
12.如图,要测量河岸相对的两点A、B之间的距离.已知垂直于河岸,现在上取两点C、D,使,过点D作的垂线,使A、C、E在一条直线上,此时,只要测出的长,即可求出的长,此方案依据的数学定理或基本事实是 .
13.如图,,是的高,且,判定的依据是 .(填写字母即可)
14.如图,点E、A、C在同一条直线上,,,,若,,则 度.
15.如图,,,点在上,连接,,若,,,,则长为 .
16.如图,,.,,垂足分别是点、,,,则的长是 .
三、解答题
17.把下面的说理过程补充完整:
已知:如图,,,,线段和线段平行吗?请说明理由.
答:,理由:
∵(已知)
∴______(等式的性质)
∴______
∵(已知)
∴ (两直线平行,内错角相等)
又∵(已知)
∴( )
∴ (全等三角形的对应角相等)
∴(内错角相等,两直线平行)
18.如图,在和中,,,且,点在上.过点作,连接.求证:;
19.如图,大小不同的两块三角板和直角顶点重合在点处,,连接,点A恰好在线段上.猜想与的位置关系,并说明理由.
20.如图,点在同一条直线上,点分别在直线的两侧,且.
(1)求证:;
(2)若,求的长.
21.如图,点在边上,.
(1)求证:;
(2)若,求的度数.
22.(1)如图1,和相交于点,,,求证:;
(2)如图2,,,,求证:.
参考答案
1.解:根据三角形的稳定性,可知:
、具有稳定性,符合题意,
、不具有稳定性,不符合题意,
、不具有稳定性,不符合题意,
、不具有稳定性,不符合题意,
故选:.
2.解:∵,,,
∴,
根据现有条件无法直接利用判定,,,
故选:C.
3.解:由作图可知,,,,
.
故答案为:A.
4.解:∵,,
∴补充,不能证明,
补充,由证明,
补充,由可证明,
故选:C.
5.解:∵如图,在△AOD中,∠O=50°,∠D=30°,
∴∠OAD=180°﹣50°﹣30°=100°,
在△AOD与△BOC中,
,
∴△AOD≌△BOC(SAS),
故∠OAD=∠OBC=100°.
在四边形OBEA中,
∠AEB=360°﹣∠OBC﹣∠OAD﹣∠O
=360°﹣100°﹣100°﹣50°
=110°,
又∵∠AEB+∠AEC=180°,
∴∠AEC=180°﹣110°=70°.
故选:A.
6.解:∵,
∴,即,
①∵,,
∴,故①正确;
添加③,
∴,故③正确;
添加④,
∴,故④正确;
添加条件②,不能证明,故②错误;
故选:C.
7.解:由1、2、3块玻璃不同时具备包括一完整边在内的三个证明全等的要素,则不能带它们去,只有第4块有完整的两角及夹边,符合,满足题目要求的条件,符合题意.
故选:D.
8.解:如图,过点作交延长线于点,
∵,,,
∴,,,
∴,
在和中,
,
∴
∴
故选:D
9.解:添加,根据可以判定,
故答案为:.
10.解:在和中,
,
∴,
∴,
故答案为:.
11.解:如图,
图中与全等的格点三角形是,共3个,
故答案为:3
12.解:∵,
∴,
∵
∴
∴
故根据全等三角形的对应边相等,只要测出的长,即可求出的长
故答案为:全等三角形的对应边相等
13.解:∵,是的高,
∴,
在与中,
,
∴,
故答案为:.
14.解:∵,,
∴
∵,
∴
∵,,
∴,
∴
故答案为:
15.解:,
,
,
,
,
,
在和中,
,
,
,,
.
故答案为:.
16.解:,,
,
.
,
.
在和中,
,
,
,.
故选答案为2.
17.解:,理由:
∵(已知)
∴(等式的性质)
∴
∵(已知)
∴(两直线平行,内错角相等)
又∵(已知)
∴()
∴(全等三角形的对应角相等)
∴(内错角相等,两直线平行)
故答案为:,,,.
18.解:∵,
∴,
∴,
在和中
∵,
∴
19.解:,理由如下:
∵
在与中,
.
.
20.(1)证明:,,且,
,
在和中,
,
.
(2)解:,
,
,
,
的长为5.
21.(1)证明:∵,
∴
∵
∴()
(2)解:∵
∴
∴,
∵
∴
∴
22.解:(1)在和中,
∴
(2)∵,
∴,
即:,
在和中,
∴
∴
∴
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
