9.3.2 一元一次不等式组的应用 课件(共30张PPT)【2024春人教七下数学精品课件含动画】
文档属性
| 名称 | 9.3.2 一元一次不等式组的应用 课件(共30张PPT)【2024春人教七下数学精品课件含动画】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 19:46:22 | ||
图片预览










文档简介
(共30张PPT)
人教七下数学同步精品课件
人教版七年级下册
情境引入
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版七(下)数学同步精品课件
9.3 一元一次不等式组
9.3.2一元一次不等式组的应用
第九章 不等式与不等式组
1.熟练掌握一元一次不等式组的解法,会用一元一次不等式组解决有关的实际问题. (重点、难点)
2.理解一元一次不等式组应用题的一般解题步骤,逐步形成分析问题和解决问题的能力.
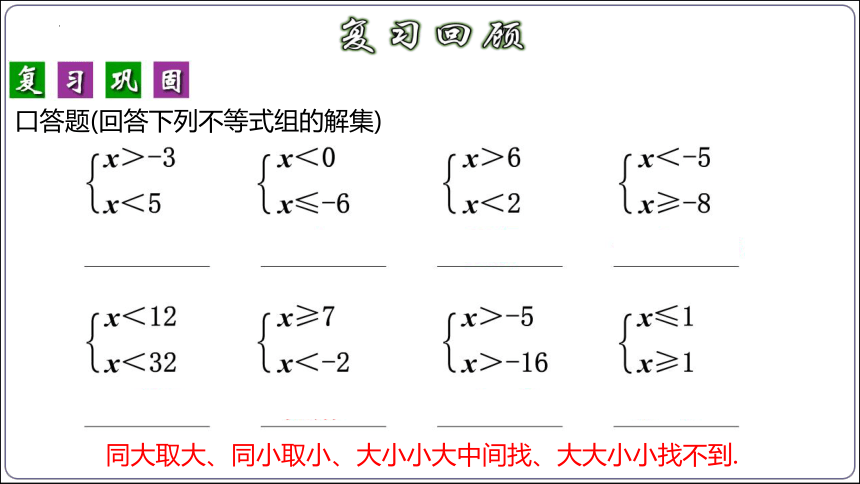
口答题(回答下列不等式组的解集)
同大取大、同小取小、大小小大中间找、大大小小找不到.
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
【分析】本题中蕴含的不等关系:
按原先的生产速度生产的产品数量<500
按后来的生产速度生产的产品数量>500
设每个小组原先每天生产x件产品
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
解:设每个小组原先每天生产x件产品,由题意,得
解不等式组,得15<x<16
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
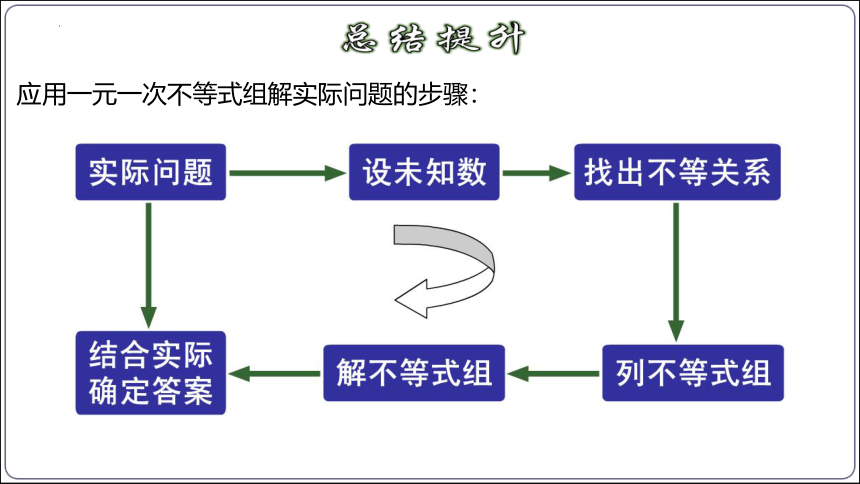
应用一元一次不等式组解实际问题的步骤:
解:设有x间宿舍,则有(4x+20)人住宿,依题意可得
解得5< x<7
因为宿舍间数是整数;
所以x=6.
住宿人数:4x+20=44(人)
答:该班有6间宿舍及44人住宿.
例1.某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
为了美化环境,张老师组织班级部分同学在操场植树,班级购买了若干树苗,若每人植棵,还剩棵,若每人植棵,最后一人有树植,但不足棵,这批树苗共有多少棵?
解:设共有人参与植树,则这批树苗共有棵,依题意得:
解得:.
又为正整数,
,
. 答:这批树苗共有棵.
例2.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案 请你设计出来.
【分析】本题不等关系:
甲种原料≤360
乙种原料≤290
A甲+ A乙
B甲+ B乙
例2.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案 请你设计出来.
解:设生产A种产品x件, B种产品(50-x)件.由题意得:
解得:30≤x≤32
∵x的值应是整数
∴x=30,31,32
例2.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案 请你设计出来.
∴有三种生产方案
方案一:A种30件,B种20件;
方案二:A种31件,B种19件;
方案三:A种32件,B种18件.
例3.某超市计划同时购进一批甲、乙两种商品,若购进甲商品10件和乙商品8件,共需要资金880元;若购进甲商品2件和乙商品5件,共需要资金380元.
(1)求甲、乙两种商品每件的进价各是多少元?
(2)该超市计划购进这两种商品共50件,而可用于购买这两种商品的资金不超过2520元.根据市场行情,销售一件甲商品可获利10元,销售一件乙商品可获利15元.该超市希望销售完这两种商品所获利润不少于620元.则该超市有哪几种进货方案?
(1)解:设甲商品每件的进价是元,乙商品每件的进价是元,根据题意得,
解得:
答:甲商品每件的进价是元,乙商品每件的进价是元;
(2)解:设购进甲商品件,则购进乙商品件,根据题意得,
解得:
∵为正整数,故
∴有三种进货方案,
方案一:购进甲商品件,乙商品件;
方案二:购进甲商品件,乙商品件;
方案三:购进甲商品件,乙商品件.
某服装店老板到厂家选购A、B两种品牌的服装,若购进A品牌服装5套,B品牌服装6套,需要950元;若购进A品牌服装3套,B品牌服装2套,需要450元.
(1)求A,B两种品牌服装每套进价分别为多少元;
(2)若销售1套A品牌服装可获利30元,销售1套B品牌的服装可获利20元,根据市场需求,服装店老板决定,购进B品牌服装的数量比购进A品牌服装数量的2倍还多4套,且B品牌服装最多可购进40套,这样服装全部售出后,可使总获利不少于1200元,问有几种进货方案?如何进货?
(1)设A种品牌服装每套进价x元,B种品牌服装每套进价y元,
根据题意得:
解得:
答:A种品牌服装每套进价100元,B种品牌服装每套进价75元;
(2)设购进A品牌m套,则购进B种品牌套,
根据题意得:
解得:,
∵m为整数,
∴m的值为16、17、18,
∴共有三种进货方案,方案一:购进A种服装16件、B种服装36件;方案二:购进A种服装17件、B种服装38件;方案三:购进A种服装18件、B种服装40件.
1.把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人能分到笔记本但数量不足4本,则共有学生( )人.
A.4人 B.5人 C.6人 D.5人或6人
2.某种出租车的收费标准是:起步价7元(即行驶距离不超过3千米都收7元车费),超过3千米以后,超过部分每增加1千米,加收2.4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共支付19元,设此人从甲地到乙地经过的路程是x千米,那么x的取值范围是( )
A. B. C. D.
D
C
3.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3200元,且购买篮球的数量不少于足球数量的一半,若每个篮球80元,每个足球50元.求共有几种购买方案?设购买篮球x个,可列不等式组( )
A. B.
C. D.
C
4.一个长方形足球场的长为xm,宽为70m,如果它的周长大于350m,面积小于7560m2,求x的取值范围,并判断这个球场是否可以用作国际足球比赛. (注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间)
解:依题意得
解这个不等式组,得105因此,该球场可以用作国际比赛.
5.一群男学生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满,可能有多少间宿舍,多少名男学生
解:如果设有x间宿舍,则男学生有(4x+19)人.依题意得:
解这个不等式组,得9.5∵x为正整数,
∴x可取整数10,11,12.
因此,当有10间宿舍时,则有59名男学生;
6.甲以5千米/时的速度进行有氧体育锻炼,2小时后,乙骑自行车从同一地出发沿同一条路追赶甲,根据他们两人的约定,乙最快不早于1小时追上甲,最慢不晚于1小时15分追上甲.那么乙骑车的速度应当控制在什么范围
解:设乙骑车的速度为x千米/时,依题意得
解这个不等式组,得13≤x≤15
答:乙骑车的速度应控制在13~15千米/时这个范围内.
7.为了美化环境,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校七年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种 请你帮助设计出来.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
解: (1) 设搭配A种造型x个,则B种造型为(50-x)个,依题意得
解这个不等式组得31≤x≤33
∵x是整数,
∴x可取31、32、 33
∴可设计三种搭配方案:
①A种园艺造型31个,B种园艺造型19个;
②A种园艺造型32个,B种园艺造型18个;
③A种园艺造型33个,B种园艺造型17个.
(2) 方案①需成本: 31×800+ 19×960=43040(元);
方案②需成本: 32×800+ 18×960=42880(元) ;
方案③需成本: 33×800+ 17×960=42720(元).
应选择方案③,成本最低,最低成本为42720元.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
应用一元一次不等式组解实际问题的步骤:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
情境引入
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版七(下)数学同步精品课件
9.3 一元一次不等式组
9.3.2一元一次不等式组的应用
第九章 不等式与不等式组
1.熟练掌握一元一次不等式组的解法,会用一元一次不等式组解决有关的实际问题. (重点、难点)
2.理解一元一次不等式组应用题的一般解题步骤,逐步形成分析问题和解决问题的能力.
口答题(回答下列不等式组的解集)
同大取大、同小取小、大小小大中间找、大大小小找不到.
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
【分析】本题中蕴含的不等关系:
按原先的生产速度生产的产品数量<500
按后来的生产速度生产的产品数量>500
设每个小组原先每天生产x件产品
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
解:设每个小组原先每天生产x件产品,由题意,得
解不等式组,得15<x<16
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
应用一元一次不等式组解实际问题的步骤:
解:设有x间宿舍,则有(4x+20)人住宿,依题意可得
解得5< x<7
因为宿舍间数是整数;
所以x=6.
住宿人数:4x+20=44(人)
答:该班有6间宿舍及44人住宿.
例1.某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
为了美化环境,张老师组织班级部分同学在操场植树,班级购买了若干树苗,若每人植棵,还剩棵,若每人植棵,最后一人有树植,但不足棵,这批树苗共有多少棵?
解:设共有人参与植树,则这批树苗共有棵,依题意得:
解得:.
又为正整数,
,
. 答:这批树苗共有棵.
例2.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案 请你设计出来.
【分析】本题不等关系:
甲种原料≤360
乙种原料≤290
A甲+ A乙
B甲+ B乙
例2.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案 请你设计出来.
解:设生产A种产品x件, B种产品(50-x)件.由题意得:
解得:30≤x≤32
∵x的值应是整数
∴x=30,31,32
例2.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案 请你设计出来.
∴有三种生产方案
方案一:A种30件,B种20件;
方案二:A种31件,B种19件;
方案三:A种32件,B种18件.
例3.某超市计划同时购进一批甲、乙两种商品,若购进甲商品10件和乙商品8件,共需要资金880元;若购进甲商品2件和乙商品5件,共需要资金380元.
(1)求甲、乙两种商品每件的进价各是多少元?
(2)该超市计划购进这两种商品共50件,而可用于购买这两种商品的资金不超过2520元.根据市场行情,销售一件甲商品可获利10元,销售一件乙商品可获利15元.该超市希望销售完这两种商品所获利润不少于620元.则该超市有哪几种进货方案?
(1)解:设甲商品每件的进价是元,乙商品每件的进价是元,根据题意得,
解得:
答:甲商品每件的进价是元,乙商品每件的进价是元;
(2)解:设购进甲商品件,则购进乙商品件,根据题意得,
解得:
∵为正整数,故
∴有三种进货方案,
方案一:购进甲商品件,乙商品件;
方案二:购进甲商品件,乙商品件;
方案三:购进甲商品件,乙商品件.
某服装店老板到厂家选购A、B两种品牌的服装,若购进A品牌服装5套,B品牌服装6套,需要950元;若购进A品牌服装3套,B品牌服装2套,需要450元.
(1)求A,B两种品牌服装每套进价分别为多少元;
(2)若销售1套A品牌服装可获利30元,销售1套B品牌的服装可获利20元,根据市场需求,服装店老板决定,购进B品牌服装的数量比购进A品牌服装数量的2倍还多4套,且B品牌服装最多可购进40套,这样服装全部售出后,可使总获利不少于1200元,问有几种进货方案?如何进货?
(1)设A种品牌服装每套进价x元,B种品牌服装每套进价y元,
根据题意得:
解得:
答:A种品牌服装每套进价100元,B种品牌服装每套进价75元;
(2)设购进A品牌m套,则购进B种品牌套,
根据题意得:
解得:,
∵m为整数,
∴m的值为16、17、18,
∴共有三种进货方案,方案一:购进A种服装16件、B种服装36件;方案二:购进A种服装17件、B种服装38件;方案三:购进A种服装18件、B种服装40件.
1.把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人能分到笔记本但数量不足4本,则共有学生( )人.
A.4人 B.5人 C.6人 D.5人或6人
2.某种出租车的收费标准是:起步价7元(即行驶距离不超过3千米都收7元车费),超过3千米以后,超过部分每增加1千米,加收2.4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共支付19元,设此人从甲地到乙地经过的路程是x千米,那么x的取值范围是( )
A. B. C. D.
D
C
3.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3200元,且购买篮球的数量不少于足球数量的一半,若每个篮球80元,每个足球50元.求共有几种购买方案?设购买篮球x个,可列不等式组( )
A. B.
C. D.
C
4.一个长方形足球场的长为xm,宽为70m,如果它的周长大于350m,面积小于7560m2,求x的取值范围,并判断这个球场是否可以用作国际足球比赛. (注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间)
解:依题意得
解这个不等式组,得105
5.一群男学生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满,可能有多少间宿舍,多少名男学生
解:如果设有x间宿舍,则男学生有(4x+19)人.依题意得:
解这个不等式组,得9.5
∴x可取整数10,11,12.
因此,当有10间宿舍时,则有59名男学生;
6.甲以5千米/时的速度进行有氧体育锻炼,2小时后,乙骑自行车从同一地出发沿同一条路追赶甲,根据他们两人的约定,乙最快不早于1小时追上甲,最慢不晚于1小时15分追上甲.那么乙骑车的速度应当控制在什么范围
解:设乙骑车的速度为x千米/时,依题意得
解这个不等式组,得13≤x≤15
答:乙骑车的速度应控制在13~15千米/时这个范围内.
7.为了美化环境,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校七年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种 请你帮助设计出来.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
解: (1) 设搭配A种造型x个,则B种造型为(50-x)个,依题意得
解这个不等式组得31≤x≤33
∵x是整数,
∴x可取31、32、 33
∴可设计三种搭配方案:
①A种园艺造型31个,B种园艺造型19个;
②A种园艺造型32个,B种园艺造型18个;
③A种园艺造型33个,B种园艺造型17个.
(2) 方案①需成本: 31×800+ 19×960=43040(元);
方案②需成本: 32×800+ 18×960=42880(元) ;
方案③需成本: 33×800+ 17×960=42720(元).
应选择方案③,成本最低,最低成本为42720元.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
应用一元一次不等式组解实际问题的步骤:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
