16.1 分式及其性质 第2课时 课件 (共26张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 16.1 分式及其性质 第2课时 课件 (共26张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 684.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
16.1 分式及其基本性质
第2课时 分式的基本性质
学 习 目 标
1.运用分式的基本性质进行分式的约分和通分.(重点)
2.灵活运用分式的基本性质将分式变形.(难点)
情 境 导 入
爷爷过生日,子女们秉承中华民族敬老、爱老的优良传统前来祝贺.爷爷很高兴,分蛋糕给大家吃.爸爸妈妈共分得其中的
,孙女分得其中的 ,小孙子分得其中的 .小孙子认为自己分的少,吵着要求重新分割,爸爸笑着说是一样的,不必重分.
思考
你会比较 , , 的大小吗?
情 境 导入
比较 , , 的大小.
分数基本性质:
分数的分子与分母同时乘以(或除)一个不等于零的数,分数的值不变.
思考
下列两式成立吗?为什么?
成立,因为分数的分子和分母同乘(或除以)一个不等于 0 的数,分数的值不变.
知 识 讲 解
知识点1 分式的基本性质
问1
分式的基本性质:分式的分子与分母都乘以(或都除以)同一个不等于零的整式,分式的值不变.
类比分数的基本性质,
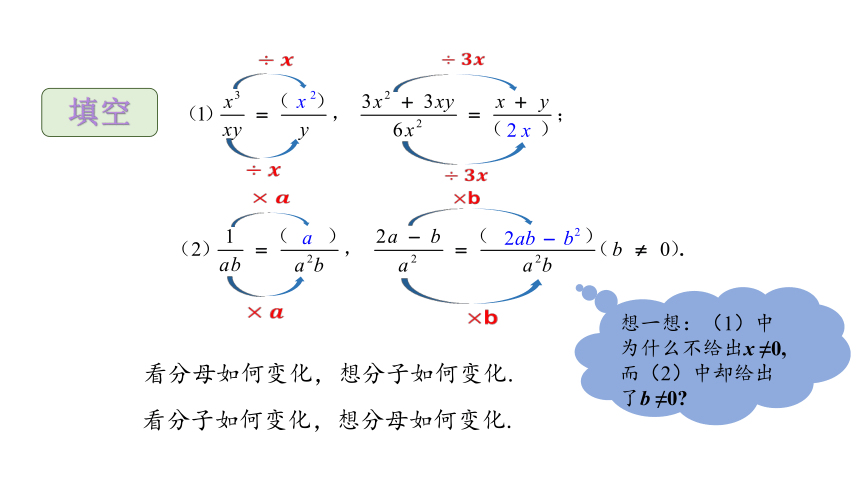
填空
看分母如何变化,想分子如何变化.
看分子如何变化,想分母如何变化.
想一想:(1)中为什么不给出x ≠0,而(2)中却给出了b ≠0
联想分数的约分,你能想出如何对分式进行约分吗?
约去分子与分母的最大公约数,化为最简分数.
思考
知 识 讲 解
知识点2 分式的约分
把分式分子、分母的公因式约去,这种变形叫分式的约分.
分式约分的依据是什么?
分式的基本性质
知 识 讲 解
知识点2 分式的约分
与分数约分类似,分式约分的关键是要找出分式的分子与分母的公因式.
例 3
约分
(1) ; (2) .
解:(1)
(2)
先分解因式,找出分子与分母的公因式,再约分.
找公因式方法
(1)系数的最大公约数
(2)分子分母相同因式的最低次幂
例 题 精 讲
讨论
在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看!
约分后,分子与分母不再有公因式.分子与分母没有公因式的分式称为最简分式.
总结归纳
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,
并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,
然后约去分子﹑分母所有的公因式.
约分的基本步骤
一般约分化简要彻底,使结果化为最简分式或整式.
随 堂 练 习
1.约分:
解:(1)
(2)
知 识 讲 解
知识点3 分式的通分
类似于分数的通分要找分母的最小公倍数,分式通分的关键是确定几个分式的最简公分母.
和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分.
知 识 讲 解
知识点3 分式的通分
最小公倍数
最简公分母
最高次幂
单独字母
找出下面各组分式的最简公分母:
通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作公分母(叫做最简公分母).
试一试
不同的因式
最简公分母的系数,取各个分母的系数的最小公倍数,字母及式子取各分母中所有字母和式子的最高次幂.
知 识 讲 解
知识点3 分式的通分
找最简公分母:
x(x-5)(x+5)
(x+y)2 (x-y)
找最简公分母:
第一看系数;第二看字母(式子).
分母是多项式的先因式分解,再找公分母.
练习
例 4
通分
(1)最简公分母:
通分:
(2)最简公分母:
通分:
解:
例 题 精 讲
最简公分母:
解:
随 堂 练 习
1.通分:
最简公分母:
通分:
通分:
解:
最简公分母:
解:
②
分数和分式在约分和通分的做法上有什么共同点?这些做法的根据是什么?
约分 通分
分数
分式
依据
找分子与分母的
最大公约数
找分子与分母的公因式
找所有分母的
最小公倍数
找所有分母的
最简公分母
分数或分式的基本性质
思考
当 堂 检 测
2. 下列各式中是最简分式的( )
B
1. 下列各式成立的是( )
A.
B.
C.
D.
D
3. 若把分式 的 x 和 y 都变为原来的两倍,则分
式的值 ( )
A.变为原来的两倍 B.不变
C.变为原来的一半 D.变为原来的四分之一
B
4. 若把分式 中的 x 和 y 都变为原来的 3 倍,则分式的值变为原来的 ( )
A.3 倍 B.9 倍 C.4 倍 D.不变
A
解:
5. 约分:
6.通分:
解:最简公分母是 2a2b2c
最简公分母是(x+5)(x-5)
分式的基本性质
内容
课 堂 小 结
作用
注意
分式进行约分和通分的依据
(1) 分子分母同时进行;
(2) 分子分母只能同乘或同除,不能进行同加或同减
(3) 分子分母只能同乘或同除同一个非零的数或式
进行分式运算的基础
16.1 分式及其基本性质
第2课时 分式的基本性质
学 习 目 标
1.运用分式的基本性质进行分式的约分和通分.(重点)
2.灵活运用分式的基本性质将分式变形.(难点)
情 境 导 入
爷爷过生日,子女们秉承中华民族敬老、爱老的优良传统前来祝贺.爷爷很高兴,分蛋糕给大家吃.爸爸妈妈共分得其中的
,孙女分得其中的 ,小孙子分得其中的 .小孙子认为自己分的少,吵着要求重新分割,爸爸笑着说是一样的,不必重分.
思考
你会比较 , , 的大小吗?
情 境 导入
比较 , , 的大小.
分数基本性质:
分数的分子与分母同时乘以(或除)一个不等于零的数,分数的值不变.
思考
下列两式成立吗?为什么?
成立,因为分数的分子和分母同乘(或除以)一个不等于 0 的数,分数的值不变.
知 识 讲 解
知识点1 分式的基本性质
问1
分式的基本性质:分式的分子与分母都乘以(或都除以)同一个不等于零的整式,分式的值不变.
类比分数的基本性质,
填空
看分母如何变化,想分子如何变化.
看分子如何变化,想分母如何变化.
想一想:(1)中为什么不给出x ≠0,而(2)中却给出了b ≠0
联想分数的约分,你能想出如何对分式进行约分吗?
约去分子与分母的最大公约数,化为最简分数.
思考
知 识 讲 解
知识点2 分式的约分
把分式分子、分母的公因式约去,这种变形叫分式的约分.
分式约分的依据是什么?
分式的基本性质
知 识 讲 解
知识点2 分式的约分
与分数约分类似,分式约分的关键是要找出分式的分子与分母的公因式.
例 3
约分
(1) ; (2) .
解:(1)
(2)
先分解因式,找出分子与分母的公因式,再约分.
找公因式方法
(1)系数的最大公约数
(2)分子分母相同因式的最低次幂
例 题 精 讲
讨论
在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看!
约分后,分子与分母不再有公因式.分子与分母没有公因式的分式称为最简分式.
总结归纳
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,
并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,
然后约去分子﹑分母所有的公因式.
约分的基本步骤
一般约分化简要彻底,使结果化为最简分式或整式.
随 堂 练 习
1.约分:
解:(1)
(2)
知 识 讲 解
知识点3 分式的通分
类似于分数的通分要找分母的最小公倍数,分式通分的关键是确定几个分式的最简公分母.
和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分.
知 识 讲 解
知识点3 分式的通分
最小公倍数
最简公分母
最高次幂
单独字母
找出下面各组分式的最简公分母:
通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作公分母(叫做最简公分母).
试一试
不同的因式
最简公分母的系数,取各个分母的系数的最小公倍数,字母及式子取各分母中所有字母和式子的最高次幂.
知 识 讲 解
知识点3 分式的通分
找最简公分母:
x(x-5)(x+5)
(x+y)2 (x-y)
找最简公分母:
第一看系数;第二看字母(式子).
分母是多项式的先因式分解,再找公分母.
练习
例 4
通分
(1)最简公分母:
通分:
(2)最简公分母:
通分:
解:
例 题 精 讲
最简公分母:
解:
随 堂 练 习
1.通分:
最简公分母:
通分:
通分:
解:
最简公分母:
解:
②
分数和分式在约分和通分的做法上有什么共同点?这些做法的根据是什么?
约分 通分
分数
分式
依据
找分子与分母的
最大公约数
找分子与分母的公因式
找所有分母的
最小公倍数
找所有分母的
最简公分母
分数或分式的基本性质
思考
当 堂 检 测
2. 下列各式中是最简分式的( )
B
1. 下列各式成立的是( )
A.
B.
C.
D.
D
3. 若把分式 的 x 和 y 都变为原来的两倍,则分
式的值 ( )
A.变为原来的两倍 B.不变
C.变为原来的一半 D.变为原来的四分之一
B
4. 若把分式 中的 x 和 y 都变为原来的 3 倍,则分式的值变为原来的 ( )
A.3 倍 B.9 倍 C.4 倍 D.不变
A
解:
5. 约分:
6.通分:
解:最简公分母是 2a2b2c
最简公分母是(x+5)(x-5)
分式的基本性质
内容
课 堂 小 结
作用
注意
分式进行约分和通分的依据
(1) 分子分母同时进行;
(2) 分子分母只能同乘或同除,不能进行同加或同减
(3) 分子分母只能同乘或同除同一个非零的数或式
进行分式运算的基础
