16.3 可化为一元一次方程的分式方程 第2课时 课件(共15张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 16.3 可化为一元一次方程的分式方程 第2课时 课件(共15张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 408.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 20:35:54 | ||
图片预览






文档简介
(共15张PPT)
16.3 可化为一元一次方程的分式方程
第2课时 分式方程的实际应用
学 习 目 标
1.理解数量关系正确列出分式方程.(难点)
2.在不同的实际问题中能审明题意设未知数,列分式方程解决实际问题.(重点)
复
习
回
顾
列一元一次方程解应用题的基本步骤是:
第一步:审题. 弄清题意,找出问题中已知量、
未知量之间的关系;借助图表分析过程.
第二步:设元. 根据题中的数量关系,将某一未知量
用字母表示,并用含该字母的代数式表示
相关未知量. (可设直接元、间接元、辅助元)
第三步:列式. 根据题中的相等关系列出一元一次方程.
第四步:求解. 解出一元一次方程的根.
第五步:检验. 看所得的解是否符合题意.
第六步:作答. (完整性,注意单位).
做一做
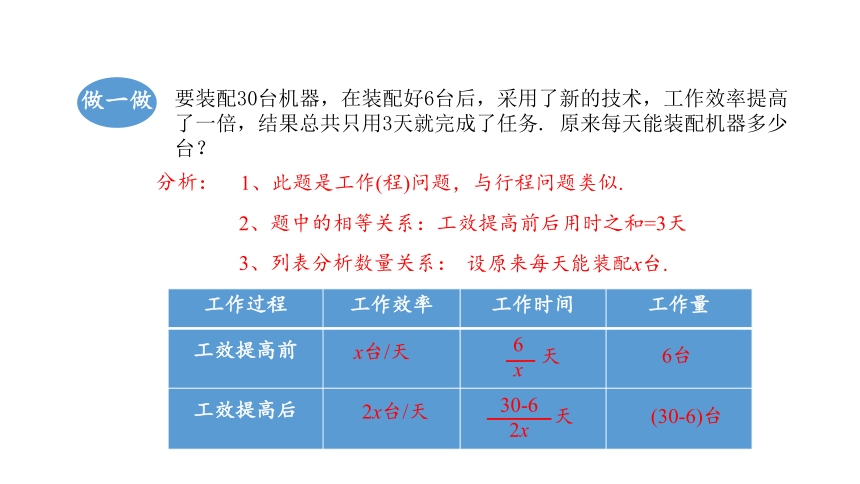
要装配30台机器,在装配好6台后,采用了新的技术,工作效率提高了一倍,结果总共只用3天就完成了任务. 原来每天能装配机器多少台?
分析:
1、此题是工作(程)问题,与行程问题类似.
2、题中的相等关系:工效提高前后用时之和=3天
3、列表分析数量关系:
工作过程 工作效率 工作时间 工作量
工效提高前
工效提高后
6台
(30-6)台
设原来每天能装配x台.
2x台/天
x台/天
6
x
天
30-6
2x
天
要装配30台机器,在装配好6台后,采用了新的技术,工作效率提高了一倍,结果总共只用3天就完成了任务. 原来每天能装配机器多少台?
解:
设原来每天能装配机器x台,由题意得
化为整式方程,得
12+24=6x
解得 x=6
经检验,x=6是原方程的解,且符合题意.
答:原来每天能装配机器6台.
6
x
30-6
2x
+ =3
知 识 讲 解
知识点1 列分式方程解应用题的基本步骤
第一步:审题. 弄清题意,找出等量关系
第二步:设元. 根据题中的等量关系,将某一未知量用字母表示. (可直接设元、间接设元)
第三步:列式. 根据题中的相等关系列分式方程.
第四步:求解. 解出分式方程的根.
第五步:检验. 看所得的解是否是增根,是否符合题意.
第六步:作答. (完整性,注意单位).
例 3
例 题 精 讲
用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2 640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完,这两个操作员每分钟各能输入多少个数据?
分析:设乙每分钟能输入x个数据
工作总量 工作效率 工作时间
甲
乙
2 640个
x个/分钟
2x个/分钟
甲工作时间=乙工作时间-(2×60)分钟
分钟
分钟
2 640个
经检验,x=11是原方程的解,并且,当x=11时,2x=22,
所以乙用了240分钟,甲用了120分钟,甲比乙少用了120分钟,符合题意.
答:甲每分钟能输入22个数据,乙每分钟能输入11个数据.
解:设乙每分钟能输入x个数据,则甲每分钟能输入2x个数据.
根据题意,得
解得x=11.
用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2 640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完,这两个操作员每分钟各能输入多少个数据?
随 堂 练 习
1.某工厂生产一批机器,由于改进生产工艺,每天比原计划多生产20台,实际生产500台机器与原计划生产300台机器所需时间相同.设实际每天生产x台机器,则可得方程( )
A. = B. =
C. = D. =
A
2.农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,
依题意得
解得 x=15
经检验,x=15是原方程的根.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
注意单位的统一.
3.A,B两地相距135千米,两辆汽车从A开往B,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟,已知小汽车与大汽车的速度之比为5:2,求两车的速度.
解:设大车速度为2x千米/时,小车速度为5x千米/时,由题意,得
解得
x=9
经检验,x=9是原方程的解,
答:大车速度为18千米/时,小车速度为45千米/时.
则2x=2×9=18,5x=5×9=45,均符合题意.
4.某进货员用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用17 600元购进2倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?
解得 x =200.
解:设第一次购进x件衬衫,由题意,得
检验:当x =200时,2x =400≠0,
所以,x =200是原分式方程的解,且符合题意.
答:第一次购进200件衬衫.
5.某工程限期完成,甲队单独做正好按期完成,乙队单独做则要误期3天. 今两队合作2天后,其余工程再由乙单独做,正好按期完工,问该工程限期是多少天
解得 x =6.
解:设该工程工期为x天,由题意,得
检验:当x =6时,x(x+3) =54≠0,
所以,x =6是原分式方程的解,且符合题意.
答:该工程工期为6天.
=1
没有工作总量时,工作总量默认为1.
课 堂 小 结
1.列分式方程解决实际问题的基本步骤:
审、设、列、求、验、答
2.常见的等量关系:
打折销售价=定价×折数
总价价=单价×数量
数量=总价÷单价
利润=售价-成本
利润率=利润÷进价.
课 后 作 业
1.从课后习题中选取;
2.完成练习册本课时的习题.
16.3 可化为一元一次方程的分式方程
第2课时 分式方程的实际应用
学 习 目 标
1.理解数量关系正确列出分式方程.(难点)
2.在不同的实际问题中能审明题意设未知数,列分式方程解决实际问题.(重点)
复
习
回
顾
列一元一次方程解应用题的基本步骤是:
第一步:审题. 弄清题意,找出问题中已知量、
未知量之间的关系;借助图表分析过程.
第二步:设元. 根据题中的数量关系,将某一未知量
用字母表示,并用含该字母的代数式表示
相关未知量. (可设直接元、间接元、辅助元)
第三步:列式. 根据题中的相等关系列出一元一次方程.
第四步:求解. 解出一元一次方程的根.
第五步:检验. 看所得的解是否符合题意.
第六步:作答. (完整性,注意单位).
做一做
要装配30台机器,在装配好6台后,采用了新的技术,工作效率提高了一倍,结果总共只用3天就完成了任务. 原来每天能装配机器多少台?
分析:
1、此题是工作(程)问题,与行程问题类似.
2、题中的相等关系:工效提高前后用时之和=3天
3、列表分析数量关系:
工作过程 工作效率 工作时间 工作量
工效提高前
工效提高后
6台
(30-6)台
设原来每天能装配x台.
2x台/天
x台/天
6
x
天
30-6
2x
天
要装配30台机器,在装配好6台后,采用了新的技术,工作效率提高了一倍,结果总共只用3天就完成了任务. 原来每天能装配机器多少台?
解:
设原来每天能装配机器x台,由题意得
化为整式方程,得
12+24=6x
解得 x=6
经检验,x=6是原方程的解,且符合题意.
答:原来每天能装配机器6台.
6
x
30-6
2x
+ =3
知 识 讲 解
知识点1 列分式方程解应用题的基本步骤
第一步:审题. 弄清题意,找出等量关系
第二步:设元. 根据题中的等量关系,将某一未知量用字母表示. (可直接设元、间接设元)
第三步:列式. 根据题中的相等关系列分式方程.
第四步:求解. 解出分式方程的根.
第五步:检验. 看所得的解是否是增根,是否符合题意.
第六步:作答. (完整性,注意单位).
例 3
例 题 精 讲
用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2 640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完,这两个操作员每分钟各能输入多少个数据?
分析:设乙每分钟能输入x个数据
工作总量 工作效率 工作时间
甲
乙
2 640个
x个/分钟
2x个/分钟
甲工作时间=乙工作时间-(2×60)分钟
分钟
分钟
2 640个
经检验,x=11是原方程的解,并且,当x=11时,2x=22,
所以乙用了240分钟,甲用了120分钟,甲比乙少用了120分钟,符合题意.
答:甲每分钟能输入22个数据,乙每分钟能输入11个数据.
解:设乙每分钟能输入x个数据,则甲每分钟能输入2x个数据.
根据题意,得
解得x=11.
用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2 640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完,这两个操作员每分钟各能输入多少个数据?
随 堂 练 习
1.某工厂生产一批机器,由于改进生产工艺,每天比原计划多生产20台,实际生产500台机器与原计划生产300台机器所需时间相同.设实际每天生产x台机器,则可得方程( )
A. = B. =
C. = D. =
A
2.农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,
依题意得
解得 x=15
经检验,x=15是原方程的根.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
注意单位的统一.
3.A,B两地相距135千米,两辆汽车从A开往B,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟,已知小汽车与大汽车的速度之比为5:2,求两车的速度.
解:设大车速度为2x千米/时,小车速度为5x千米/时,由题意,得
解得
x=9
经检验,x=9是原方程的解,
答:大车速度为18千米/时,小车速度为45千米/时.
则2x=2×9=18,5x=5×9=45,均符合题意.
4.某进货员用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用17 600元购进2倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?
解得 x =200.
解:设第一次购进x件衬衫,由题意,得
检验:当x =200时,2x =400≠0,
所以,x =200是原分式方程的解,且符合题意.
答:第一次购进200件衬衫.
5.某工程限期完成,甲队单独做正好按期完成,乙队单独做则要误期3天. 今两队合作2天后,其余工程再由乙单独做,正好按期完工,问该工程限期是多少天
解得 x =6.
解:设该工程工期为x天,由题意,得
检验:当x =6时,x(x+3) =54≠0,
所以,x =6是原分式方程的解,且符合题意.
答:该工程工期为6天.
=1
没有工作总量时,工作总量默认为1.
课 堂 小 结
1.列分式方程解决实际问题的基本步骤:
审、设、列、求、验、答
2.常见的等量关系:
打折销售价=定价×折数
总价价=单价×数量
数量=总价÷单价
利润=售价-成本
利润率=利润÷进价.
课 后 作 业
1.从课后习题中选取;
2.完成练习册本课时的习题.
