17.2 函数的图象 第1课时 课件(共26张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 17.2 函数的图象 第1课时 课件(共26张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 898.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
17.2 函数的图象
第1课时 平面直角坐标系
学 习 目 标
1.理解平面直角坐标系的概念,平面直角坐标系内的点与和有序实数对的一一对应关系.(重点)
2.会画平面直角坐标系,在给定的直角坐标系中,能由坐标找点、由点找坐标.(重点)
3.探索并掌握特殊位置的点以及对称点的坐标特征.(难点)
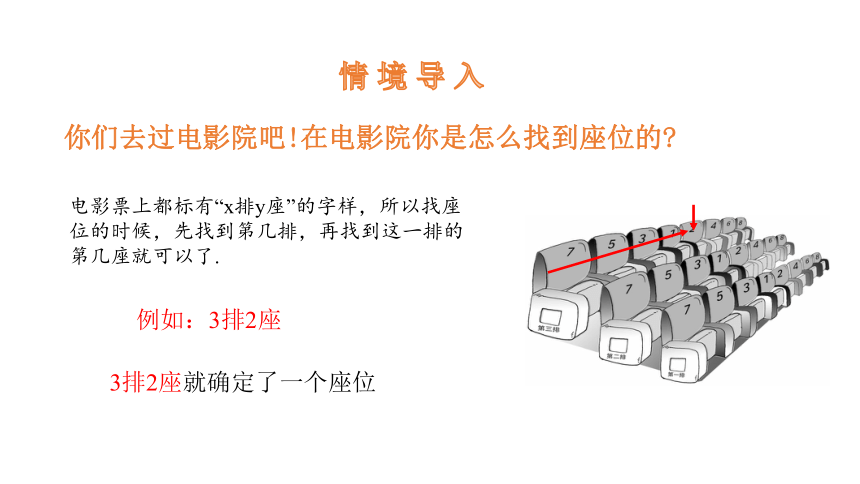
情 境 导 入
你们去过电影院吧!在电影院你是怎么找到座位的
例如:3排2座
3排2座就确定了一个座位
电影票上都标有“x排y座”的字样,所以找座位的时候,先找到第几排,再找到这一排的第几座就可以了.
知 识 讲 解
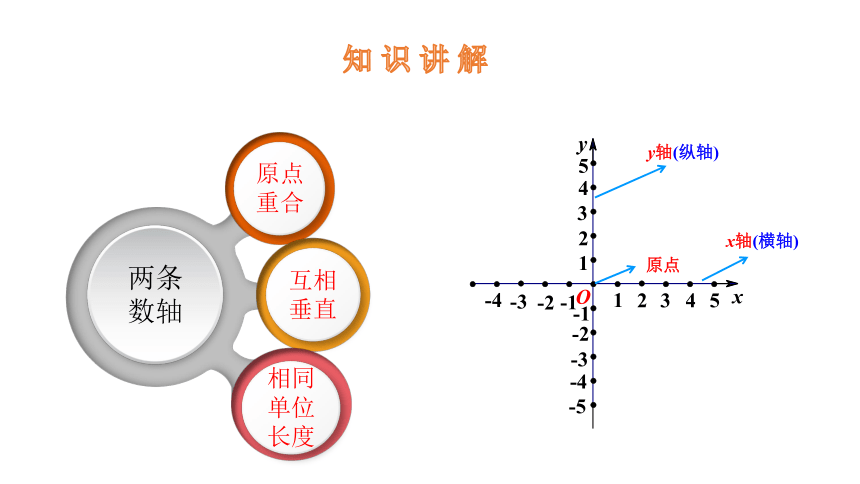
知识点1 平面直角坐标系的概念
平面直角坐标系:平面上,两条原点重合、互相垂直且具有相同单位长度的数轴,组成了平面直角坐标系.
通常把其中水平的数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两条数轴的交点O叫做坐标原点.
在数学中,我们可以用一对有序实数来确定平面上点的位置.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
原点
x轴(横轴)
y轴(纵轴)
两条数轴
原点重合
互相垂直
相同单位长度
知 识 讲 解
3
2
1
-1
-2
-3
P
-4 -3 -2 -1 0 1 2 3 4 5 6
y
x
知 识 讲 解
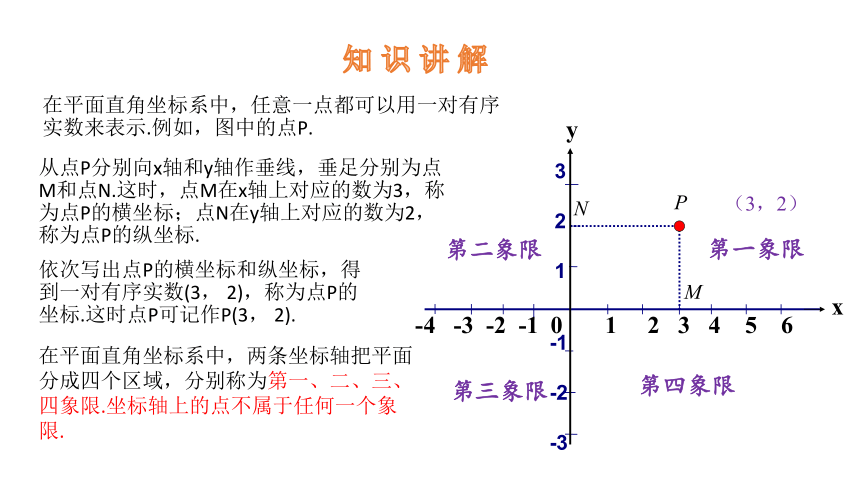
在平面直角坐标系中,任意一点都可以用一对有序实数来表示.例如,图中的点P.
M
N
从点P分别向x轴和y轴作垂线,垂足分别为点M和点N.这时,点M在x轴上对应的数为3,称为点P的横坐标;点N在y轴上对应的数为2,称为点P的纵坐标.
依次写出点P的横坐标和纵坐标,得到一对有序实数(3, 2),称为点P的坐标.这时点P可记作P(3, 2).
在平面直角坐标系中,两条坐标轴把平面分成四个区域,分别称为第一、二、三、四象限.坐标轴上的点不属于任何一个象限.
第一象限
第二象限
第三象限
第四象限
(3,2)
例 1
例 题 精 讲
下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的垂足是原点
B.平面直角坐标系所在的平面叫做坐标平面
C.平面直角坐标系中,x轴、y轴把坐标平面分成四部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系
D
试一试
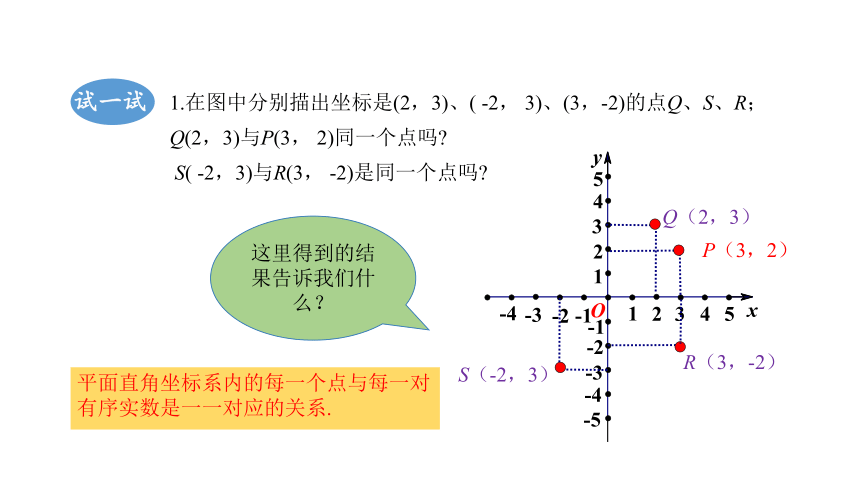
1.在图中分别描出坐标是(2,3)、( -2, 3)、(3,-2)的点Q、S、R;
Q(2,3)与P(3, 2)同一个点吗
S( -2,3)与R(3, -2)是同一个点吗
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
Q(2,3)
S(-2,3)
R(3,-2)
P(3,2)
这里得到的结果告诉我们什么?
平面直角坐标系内的每一个点与每一对
有序实数是一一对应的关系.
2.写出图17.2.3中的点A、B、C、D、E、F的坐标.观察你所写出的这些点的坐标,思考:
(1)在四个象限内的点的坐标各有什么特征
(2)两条坐标轴上的点的坐标各有什么特征
试一试
(-1,2)
(2,-1)
(2,1)
(-1,2)
(-2,0)
(1)各象限内点的特点:
点M(x,y)所处的位置 坐标特征
象限内 的点 点M在第一象限 M(正,正)
点M在第二象限 M(负,正)
点M在第三象限 M(负,负)
点M在第四象限 M(正,负)
(2)各象限内点的特点:
x轴上的点纵坐标都为0,y轴上的点的坐标横坐标都为0.
随 堂 练 习
A(5,2)
B(0,5)
C(-5,2)
D(-3,-4)
E(3,-4)
1.如图,分别写出五边形各个顶点的坐标.
2.已知:点M(x,y)在第四象限且=3,=4,求点M 的坐标.
M(3,-4).
3.已知:点M(x,y)在第二象限,且x+y=2,请写出两个符合条件的点M的坐标.
M(-1,3),M(-3,5)(答案不唯一,只要同时满足x<0,y>0,x+y=2即可).
4.以长途汽车总站为坐标原点,幸福街为x轴,向阳路为y轴建立平面直角坐标系,纪念馆的位置如图所示,则其所覆盖的坐标可能是( )
C
A.(﹣5,3)
B.(4,3)
C.(5,﹣3)
D.(﹣5,﹣3)
1.如图:点B与C的纵坐标相同,线段BC与横轴在位置有什么特点?
2.线段CE与纵轴在位置又有什么特点?
想一想
你能由此发现什么规律?
平行于x轴
平行于y轴
知识点2 与坐标轴平行的直线上的点的坐标特征
知 识 讲 解
平行于x轴的直线上的点的纵坐标相等;
平行于y轴的直线上的点的横坐标相等.
1.下列各点中,在第二象限的点是( )
A.( 2,3) B.(2,-1) C.(-2,-6) D.(-1,2 )
2.已知点A(m ,2)在y轴上,则m+1等于( )
A.-1 B.1 C.0 D.±1
3.已知点A(a ,b)在第四象限,则点B(b,a)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
B
D
随 堂 练 习
问题
1.如图所示的平面直角坐标系中,第一、四象限内各有一个笑脸.
(1)两个笑脸之间有怎样的位置关系?
关于x轴成轴对称
(2)它们的对应点的坐标之间有什么特点?
横坐标相等,纵坐标互为相反数
2.如图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
关于y轴成轴对称
(2)对应点A与A1的坐标有什么共同特点?
其他对应的点也有这个特点吗?
纵坐标相等,横坐标互为相反数
知识点3 关于坐标轴对称的两个点的坐标特征
知 识 讲 解
关于x轴对称点的坐标的特征:
(1) 横坐标相同,纵坐标互为相反数.
(2)用坐标表示轴对称的性质: 点P(x,y)关于x轴对称的点的坐标为(x,-y).
关于y轴对称点的坐标的特征:
(1) 纵坐标相同,横坐标互为相反数.
(2)用坐标表示轴对称的性质:点P(x,y)关于x轴对称的点的坐标为(-x,y).
若两个点关于原点对称,它们的坐标有什么特点呢?
随 堂 练 习
1.点(4,3)与点(4,- 3)的关系是( )
A.关于原点对称
B.关于 x轴对称
C.关于 y轴对称
D.不能构成对称关系
B
2.已知点A ( a ,2)与点B(3,b )关于y轴对称,则实数a ,b 的值是( )
A.a =3,b=2
B.a =﹣3,b =2
C.a =3,b=﹣2
D.a=﹣3,b =﹣2
B
3.如图,长方形ABCD的边CD在y轴上,原点О为C的中点.已知AB=4,边AB交x 轴于点E(﹣5,0),则点B的坐标为( )
A.(﹣5,2)
B.(﹣2,﹣5)
C.(5,﹣2)
D.(﹣5,﹣2 )
A
4.已知点A,B的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①点A,B关于x轴对称;②点A, B关于y轴对称;③点A在第二象限,点B在第一象限;④点A,B之间的距离为4.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
当 堂 检 测
1.在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
2.如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(-6,3)
C.(-4,-6) D.(3,-4)
D
3. 在直线l上有两点P1(x1,y1)、P2(x2,y2),若直线l∥x轴,则下列结论正确的是( )
x1=x2 B. x1+x2=0
C. y1=y2 D. y1+y2=0
C
4.已知点A(x,y ),且xy=0,则点A 在( )
A.原点 B.x 轴上
C.y 轴上 D.x轴或y轴上
D
5.点P (-3,4)关于x轴的对称点的坐标为 ;关于y轴的对称点的坐标为 ;关于原点的对称点的坐标为 .
(-3,-4)
(3,-4)
(3,4)
6. 已知A(a,6),B(2,b)两点.
⑴. 若A、B关于x轴对称,a=_____;b=_____.
⑵. 若A、B关于y轴对称,a=_____;b=_____.
⑶. 若A、B关于原点对称,a=_____;b=_____.
2
-6
-2
6
-2
-6
课 堂 小 结
1.能够正确画出直角坐标系.
2.能在直角坐标系中,根据坐标找出点,由点求出坐标.
坐标平面内的点和有序实数对是一一对应的。
3.掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4、平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同.
①关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
如P(x,y)关于x轴对称的点的坐标为P1(x,-y);
②关于y轴对称的两点,纵坐标相同,横坐标互为相反数,
如P(x,y)关于y轴对称的点的坐标为P2(-x,y);
③关于原点对称的两点,横、纵坐标分别互为相反数,
如P(x,y)关于原点对称的点的坐标为P3(-x,-y).
5、特殊点的坐标的特征
17.2 函数的图象
第1课时 平面直角坐标系
学 习 目 标
1.理解平面直角坐标系的概念,平面直角坐标系内的点与和有序实数对的一一对应关系.(重点)
2.会画平面直角坐标系,在给定的直角坐标系中,能由坐标找点、由点找坐标.(重点)
3.探索并掌握特殊位置的点以及对称点的坐标特征.(难点)
情 境 导 入
你们去过电影院吧!在电影院你是怎么找到座位的
例如:3排2座
3排2座就确定了一个座位
电影票上都标有“x排y座”的字样,所以找座位的时候,先找到第几排,再找到这一排的第几座就可以了.
知 识 讲 解
知识点1 平面直角坐标系的概念
平面直角坐标系:平面上,两条原点重合、互相垂直且具有相同单位长度的数轴,组成了平面直角坐标系.
通常把其中水平的数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两条数轴的交点O叫做坐标原点.
在数学中,我们可以用一对有序实数来确定平面上点的位置.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
原点
x轴(横轴)
y轴(纵轴)
两条数轴
原点重合
互相垂直
相同单位长度
知 识 讲 解
3
2
1
-1
-2
-3
P
-4 -3 -2 -1 0 1 2 3 4 5 6
y
x
知 识 讲 解
在平面直角坐标系中,任意一点都可以用一对有序实数来表示.例如,图中的点P.
M
N
从点P分别向x轴和y轴作垂线,垂足分别为点M和点N.这时,点M在x轴上对应的数为3,称为点P的横坐标;点N在y轴上对应的数为2,称为点P的纵坐标.
依次写出点P的横坐标和纵坐标,得到一对有序实数(3, 2),称为点P的坐标.这时点P可记作P(3, 2).
在平面直角坐标系中,两条坐标轴把平面分成四个区域,分别称为第一、二、三、四象限.坐标轴上的点不属于任何一个象限.
第一象限
第二象限
第三象限
第四象限
(3,2)
例 1
例 题 精 讲
下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的垂足是原点
B.平面直角坐标系所在的平面叫做坐标平面
C.平面直角坐标系中,x轴、y轴把坐标平面分成四部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系
D
试一试
1.在图中分别描出坐标是(2,3)、( -2, 3)、(3,-2)的点Q、S、R;
Q(2,3)与P(3, 2)同一个点吗
S( -2,3)与R(3, -2)是同一个点吗
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
Q(2,3)
S(-2,3)
R(3,-2)
P(3,2)
这里得到的结果告诉我们什么?
平面直角坐标系内的每一个点与每一对
有序实数是一一对应的关系.
2.写出图17.2.3中的点A、B、C、D、E、F的坐标.观察你所写出的这些点的坐标,思考:
(1)在四个象限内的点的坐标各有什么特征
(2)两条坐标轴上的点的坐标各有什么特征
试一试
(-1,2)
(2,-1)
(2,1)
(-1,2)
(-2,0)
(1)各象限内点的特点:
点M(x,y)所处的位置 坐标特征
象限内 的点 点M在第一象限 M(正,正)
点M在第二象限 M(负,正)
点M在第三象限 M(负,负)
点M在第四象限 M(正,负)
(2)各象限内点的特点:
x轴上的点纵坐标都为0,y轴上的点的坐标横坐标都为0.
随 堂 练 习
A(5,2)
B(0,5)
C(-5,2)
D(-3,-4)
E(3,-4)
1.如图,分别写出五边形各个顶点的坐标.
2.已知:点M(x,y)在第四象限且=3,=4,求点M 的坐标.
M(3,-4).
3.已知:点M(x,y)在第二象限,且x+y=2,请写出两个符合条件的点M的坐标.
M(-1,3),M(-3,5)(答案不唯一,只要同时满足x<0,y>0,x+y=2即可).
4.以长途汽车总站为坐标原点,幸福街为x轴,向阳路为y轴建立平面直角坐标系,纪念馆的位置如图所示,则其所覆盖的坐标可能是( )
C
A.(﹣5,3)
B.(4,3)
C.(5,﹣3)
D.(﹣5,﹣3)
1.如图:点B与C的纵坐标相同,线段BC与横轴在位置有什么特点?
2.线段CE与纵轴在位置又有什么特点?
想一想
你能由此发现什么规律?
平行于x轴
平行于y轴
知识点2 与坐标轴平行的直线上的点的坐标特征
知 识 讲 解
平行于x轴的直线上的点的纵坐标相等;
平行于y轴的直线上的点的横坐标相等.
1.下列各点中,在第二象限的点是( )
A.( 2,3) B.(2,-1) C.(-2,-6) D.(-1,2 )
2.已知点A(m ,2)在y轴上,则m+1等于( )
A.-1 B.1 C.0 D.±1
3.已知点A(a ,b)在第四象限,则点B(b,a)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
B
D
随 堂 练 习
问题
1.如图所示的平面直角坐标系中,第一、四象限内各有一个笑脸.
(1)两个笑脸之间有怎样的位置关系?
关于x轴成轴对称
(2)它们的对应点的坐标之间有什么特点?
横坐标相等,纵坐标互为相反数
2.如图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
关于y轴成轴对称
(2)对应点A与A1的坐标有什么共同特点?
其他对应的点也有这个特点吗?
纵坐标相等,横坐标互为相反数
知识点3 关于坐标轴对称的两个点的坐标特征
知 识 讲 解
关于x轴对称点的坐标的特征:
(1) 横坐标相同,纵坐标互为相反数.
(2)用坐标表示轴对称的性质: 点P(x,y)关于x轴对称的点的坐标为(x,-y).
关于y轴对称点的坐标的特征:
(1) 纵坐标相同,横坐标互为相反数.
(2)用坐标表示轴对称的性质:点P(x,y)关于x轴对称的点的坐标为(-x,y).
若两个点关于原点对称,它们的坐标有什么特点呢?
随 堂 练 习
1.点(4,3)与点(4,- 3)的关系是( )
A.关于原点对称
B.关于 x轴对称
C.关于 y轴对称
D.不能构成对称关系
B
2.已知点A ( a ,2)与点B(3,b )关于y轴对称,则实数a ,b 的值是( )
A.a =3,b=2
B.a =﹣3,b =2
C.a =3,b=﹣2
D.a=﹣3,b =﹣2
B
3.如图,长方形ABCD的边CD在y轴上,原点О为C的中点.已知AB=4,边AB交x 轴于点E(﹣5,0),则点B的坐标为( )
A.(﹣5,2)
B.(﹣2,﹣5)
C.(5,﹣2)
D.(﹣5,﹣2 )
A
4.已知点A,B的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①点A,B关于x轴对称;②点A, B关于y轴对称;③点A在第二象限,点B在第一象限;④点A,B之间的距离为4.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
当 堂 检 测
1.在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
2.如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(-6,3)
C.(-4,-6) D.(3,-4)
D
3. 在直线l上有两点P1(x1,y1)、P2(x2,y2),若直线l∥x轴,则下列结论正确的是( )
x1=x2 B. x1+x2=0
C. y1=y2 D. y1+y2=0
C
4.已知点A(x,y ),且xy=0,则点A 在( )
A.原点 B.x 轴上
C.y 轴上 D.x轴或y轴上
D
5.点P (-3,4)关于x轴的对称点的坐标为 ;关于y轴的对称点的坐标为 ;关于原点的对称点的坐标为 .
(-3,-4)
(3,-4)
(3,4)
6. 已知A(a,6),B(2,b)两点.
⑴. 若A、B关于x轴对称,a=_____;b=_____.
⑵. 若A、B关于y轴对称,a=_____;b=_____.
⑶. 若A、B关于原点对称,a=_____;b=_____.
2
-6
-2
6
-2
-6
课 堂 小 结
1.能够正确画出直角坐标系.
2.能在直角坐标系中,根据坐标找出点,由点求出坐标.
坐标平面内的点和有序实数对是一一对应的。
3.掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4、平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同.
①关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
如P(x,y)关于x轴对称的点的坐标为P1(x,-y);
②关于y轴对称的两点,纵坐标相同,横坐标互为相反数,
如P(x,y)关于y轴对称的点的坐标为P2(-x,y);
③关于原点对称的两点,横、纵坐标分别互为相反数,
如P(x,y)关于原点对称的点的坐标为P3(-x,-y).
5、特殊点的坐标的特征
