17.5 实践与探索 第2课时 课件 (共15张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 17.5 实践与探索 第2课时 课件 (共15张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 398.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
17.5 实践与探索
第2课时 一次函数的实际应用
学 习 目 标
1.能够使用一次函数思想解决实际问题.(重点)
2.会用一次函数与一元一次方程和一元一次不等式的关系解决实际问题.(难点)
2.一次函数与一元一次不等式的关系?
1.一次函数与一元方程(组)的关系?
情 境 导 入
复
习
回
顾
问题3
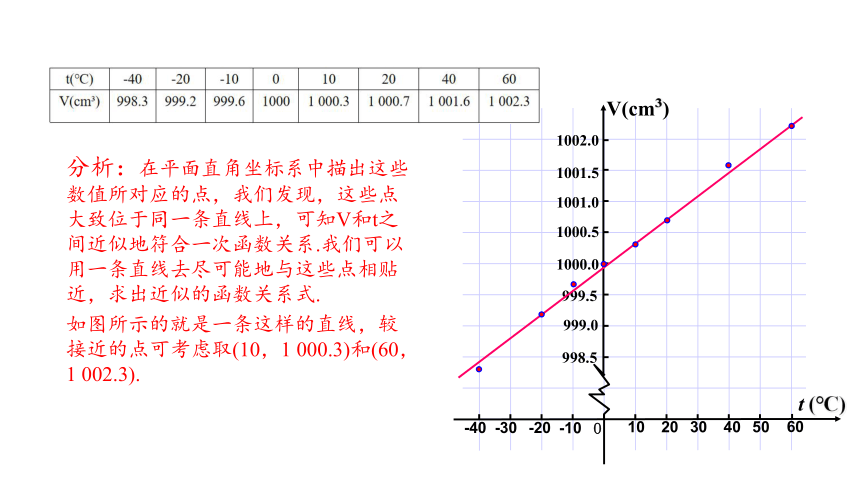
t(℃) -40 -20 -10 0 10 20 40 60
V(cm ) 998.3 999.2 999.6 1000 1 000.3 1 000.7 1 001.6 1 002.3
为了研究某合金材料的体积V(cm )随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系
10
20
30
40
50
O
-10
-20
-30
-40
t (℃)
60
V(cm )
998.5
999.0
999.5
1000.0
1000.5
1001.0
1001.5
1002.0
分析:在平面直角坐标系中描出这些数值所对应的点,我们发现,这些点大致位于同一条直线上,可知V和t之间近似地符合一次函数关系.我们可以用一条直线去尽可能地与这些点相贴近,求出近似的函数关系式.
如图所示的就是一条这样的直线,较接近的点可考虑取(10,1 000.3)和(60, 1 002.3).
根据图象得,
V与t的函数关系式:
V=kt+b(k≠0),
1000.3 =10k+b
1002.3 =60k+b
由表中数据可知,
t=10时, V=1000.3; t=60时, V=1002.3
∴
∴
k=0.04
b=999.9
∴ V=0.04t+999.9
解:
总结归纳
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
例 1
例 题 精 讲
电阻R(欧姆) 2 4 6 8 10 12
电流I(安培) 6 3 2 1.5 1.2 1
R
A
小明在做电学实验时,电路图如图所示.在保持电压不变的情况下,改换不同的电阻R,并用电流表测量出通过不同电阻的电流I,记录结果如下:
(1)建立适当的平面直角坐标系,在坐标系中描出表格中的各点,并画出该函数的近似图象;
(2)观察图象,猜想I与R之间的函数关系,并求出函数解析式;
(3)小明将一个未知电阻值的电阻串联到电路中,查得电流表的度数为0.5安培,你知道这个电阻的电阻值吗
8
4
12
O
R(欧姆)
2
4
6
I(安培)
解:(1)用描点法画出表格中的各点,可得函数的近似图象(如图所示),
设I与R之间的函数关系为:I=k/R
∵I=2时,R=6
∴k=2×6=12
电阻R(欧姆) 2 4 6 8 10 12
电流I(安培) 6 3 2 1.5 1.2 1
∴I=12/R
(3)当I=0.5时,R=12/0.5=24.
(2)由近似图象可知,是反比例函数.
随 堂 练 习
1.某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元,该店制定了两种优惠方案:①买一个书包赠送一个文具盒;②按总价九折付款,某班需购8个书包,文具盒若干个(不少于8个),如果设购文具盒为x个,付款y元.
(1)分别求出两种优惠方案中y与x之间的函数关系式。
(2)在同一平面直角坐标中画出函数图象,根据图象回答,购买多少个文具盒两种方案用钱相同。
解:(1)①y①=30×8+5(x-8)=5x+200,
②y②=(30×8+5x)×90%=4.5x+216.
(2)由图象可知,有交点,联立组成方程组求解x=32,y=360.
2.某公司到果园基地购买某种优质水果,慰问医务工作者.果园基地对购买量在3 000千克以上(含3 000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5 000元.
(1)分别写出该公司两种购买方案的付款y(元)与所买的水果量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.
解 :
(1) y甲=9x
(x≥3 000)
y乙=8x+5 000
(x≥3 000)
(2)当 y甲= y乙,即9x=8x+5000时,
解得x=5000.
所以当x=5000时,两种付款一样;
解得3000≤x<5000.
所以当3000≤x<5000时,选择甲方案付款最少;
解得x>5000.
所以当x>5000时,选择乙方案付款最少.
当 y甲< y乙时,有
x≥3000
9x<8x+5000
当 y甲> y乙时,
有9x>8x+5000
3.为了防止水灾后的疫情发生,决定将甲、乙两医药仓库的某药品的80箱和70箱,送给灾区A县100箱,B县50箱。从甲、乙两仓库运往A县和B县的运费情况如下表:
(1)若设甲仓库运往A县的药品箱数为x,总运费为y元,请写出y与x的函数关系式;
(2)这150箱药品如何调配运送,既能按要求的数量配发,又能使总费最低?
到 站 费用(元/桶)
甲库 乙库
A县 7 4
B县 5 10
到 站 费用(元/桶)
甲库 乙库
A县 7 4
B县 5 10
解:(1)设甲仓库运往A县的药品箱数为x,则甲仓库运往B县80-x,乙仓库运往A县100- x,乙仓库运往B 县70-(100- x)根据题意有:
甲库 乙库 A县 B县
80 70 100 50
x
80-x
100-x
70-(100-x)
(2)∵y =8x+500,
∴费用y随x增大而增大,减小而减小,
∴费用y要最少,箱数x必最少,
∵ 30≤x≤80,
∴ x=30时,费用y最少,
即y =760.
课 堂 小 结
1.将已知的这些有序数对作为点的坐标在坐标平面内描出相应的点;
2.对比已经学过的函数图象,确定这些点组成的图形类似于某一类函数图象,并写出这一函数的一般式;
3.通过已知点的坐标确定函数一般式中待定系数的值;
4.写实际问题中的函数关系;
5.根据函数关系和图象解决相关问题.
17.5 实践与探索
第2课时 一次函数的实际应用
学 习 目 标
1.能够使用一次函数思想解决实际问题.(重点)
2.会用一次函数与一元一次方程和一元一次不等式的关系解决实际问题.(难点)
2.一次函数与一元一次不等式的关系?
1.一次函数与一元方程(组)的关系?
情 境 导 入
复
习
回
顾
问题3
t(℃) -40 -20 -10 0 10 20 40 60
V(cm ) 998.3 999.2 999.6 1000 1 000.3 1 000.7 1 001.6 1 002.3
为了研究某合金材料的体积V(cm )随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系
10
20
30
40
50
O
-10
-20
-30
-40
t (℃)
60
V(cm )
998.5
999.0
999.5
1000.0
1000.5
1001.0
1001.5
1002.0
分析:在平面直角坐标系中描出这些数值所对应的点,我们发现,这些点大致位于同一条直线上,可知V和t之间近似地符合一次函数关系.我们可以用一条直线去尽可能地与这些点相贴近,求出近似的函数关系式.
如图所示的就是一条这样的直线,较接近的点可考虑取(10,1 000.3)和(60, 1 002.3).
根据图象得,
V与t的函数关系式:
V=kt+b(k≠0),
1000.3 =10k+b
1002.3 =60k+b
由表中数据可知,
t=10时, V=1000.3; t=60时, V=1002.3
∴
∴
k=0.04
b=999.9
∴ V=0.04t+999.9
解:
总结归纳
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
例 1
例 题 精 讲
电阻R(欧姆) 2 4 6 8 10 12
电流I(安培) 6 3 2 1.5 1.2 1
R
A
小明在做电学实验时,电路图如图所示.在保持电压不变的情况下,改换不同的电阻R,并用电流表测量出通过不同电阻的电流I,记录结果如下:
(1)建立适当的平面直角坐标系,在坐标系中描出表格中的各点,并画出该函数的近似图象;
(2)观察图象,猜想I与R之间的函数关系,并求出函数解析式;
(3)小明将一个未知电阻值的电阻串联到电路中,查得电流表的度数为0.5安培,你知道这个电阻的电阻值吗
8
4
12
O
R(欧姆)
2
4
6
I(安培)
解:(1)用描点法画出表格中的各点,可得函数的近似图象(如图所示),
设I与R之间的函数关系为:I=k/R
∵I=2时,R=6
∴k=2×6=12
电阻R(欧姆) 2 4 6 8 10 12
电流I(安培) 6 3 2 1.5 1.2 1
∴I=12/R
(3)当I=0.5时,R=12/0.5=24.
(2)由近似图象可知,是反比例函数.
随 堂 练 习
1.某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元,该店制定了两种优惠方案:①买一个书包赠送一个文具盒;②按总价九折付款,某班需购8个书包,文具盒若干个(不少于8个),如果设购文具盒为x个,付款y元.
(1)分别求出两种优惠方案中y与x之间的函数关系式。
(2)在同一平面直角坐标中画出函数图象,根据图象回答,购买多少个文具盒两种方案用钱相同。
解:(1)①y①=30×8+5(x-8)=5x+200,
②y②=(30×8+5x)×90%=4.5x+216.
(2)由图象可知,有交点,联立组成方程组求解x=32,y=360.
2.某公司到果园基地购买某种优质水果,慰问医务工作者.果园基地对购买量在3 000千克以上(含3 000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5 000元.
(1)分别写出该公司两种购买方案的付款y(元)与所买的水果量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.
解 :
(1) y甲=9x
(x≥3 000)
y乙=8x+5 000
(x≥3 000)
(2)当 y甲= y乙,即9x=8x+5000时,
解得x=5000.
所以当x=5000时,两种付款一样;
解得3000≤x<5000.
所以当3000≤x<5000时,选择甲方案付款最少;
解得x>5000.
所以当x>5000时,选择乙方案付款最少.
当 y甲< y乙时,有
x≥3000
9x<8x+5000
当 y甲> y乙时,
有9x>8x+5000
3.为了防止水灾后的疫情发生,决定将甲、乙两医药仓库的某药品的80箱和70箱,送给灾区A县100箱,B县50箱。从甲、乙两仓库运往A县和B县的运费情况如下表:
(1)若设甲仓库运往A县的药品箱数为x,总运费为y元,请写出y与x的函数关系式;
(2)这150箱药品如何调配运送,既能按要求的数量配发,又能使总费最低?
到 站 费用(元/桶)
甲库 乙库
A县 7 4
B县 5 10
到 站 费用(元/桶)
甲库 乙库
A县 7 4
B县 5 10
解:(1)设甲仓库运往A县的药品箱数为x,则甲仓库运往B县80-x,乙仓库运往A县100- x,乙仓库运往B 县70-(100- x)根据题意有:
甲库 乙库 A县 B县
80 70 100 50
x
80-x
100-x
70-(100-x)
(2)∵y =8x+500,
∴费用y随x增大而增大,减小而减小,
∴费用y要最少,箱数x必最少,
∵ 30≤x≤80,
∴ x=30时,费用y最少,
即y =760.
课 堂 小 结
1.将已知的这些有序数对作为点的坐标在坐标平面内描出相应的点;
2.对比已经学过的函数图象,确定这些点组成的图形类似于某一类函数图象,并写出这一函数的一般式;
3.通过已知点的坐标确定函数一般式中待定系数的值;
4.写实际问题中的函数关系;
5.根据函数关系和图象解决相关问题.
