18.1 平行四边形的性质 第1课时 课件(共25张PPT) 2023-2024学年数学华师大版八年级下册
文档属性
| 名称 | 18.1 平行四边形的性质 第1课时 课件(共25张PPT) 2023-2024学年数学华师大版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 714.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
18.1 平行四边形的性质
第1课时 平行四边形的性质定理1、2
学 习 目 标
1.理解并掌握平行四边形的概念.
2.探索平行四边形的中心对称性质.
3.探索并证明平行四边形的性质定理:对边相等,对角相等.(重点)
4.灵活运用平行四边形的性质解决简单的平行四边形的计算、证明问题.(难点)
情 境 导 入
平行四边形是随处可见的几何图形.生活中,你还见过哪些平行四边形?用自己的语言描述一下什么样的图形叫做平行四边形.
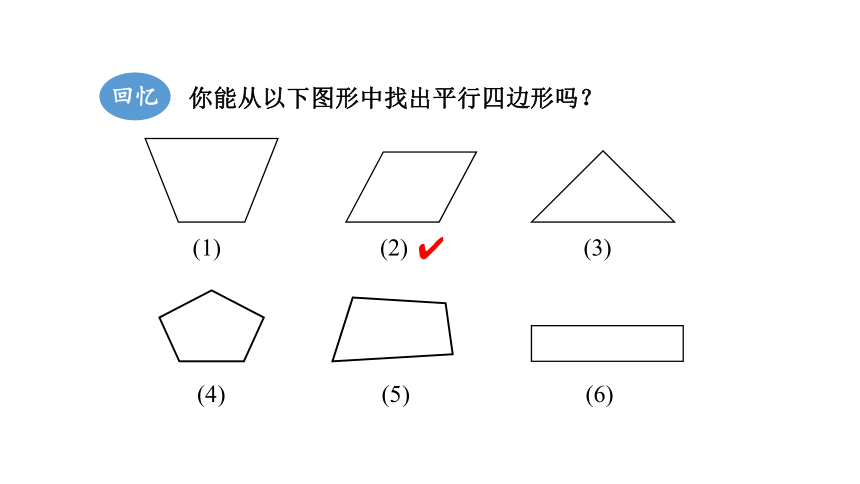
回忆
你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
(6)
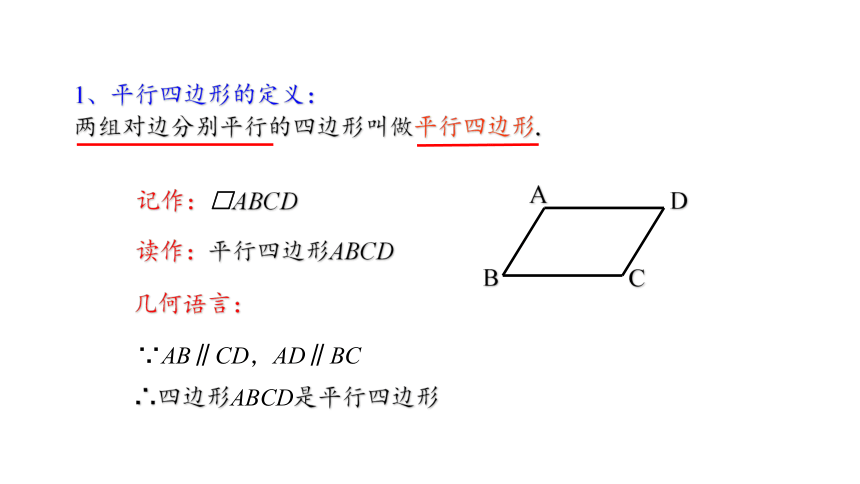
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
∴四边形ABCD是平行四边形
几何语言:
∵AB∥CD,AD∥BC
记作:□ABCD
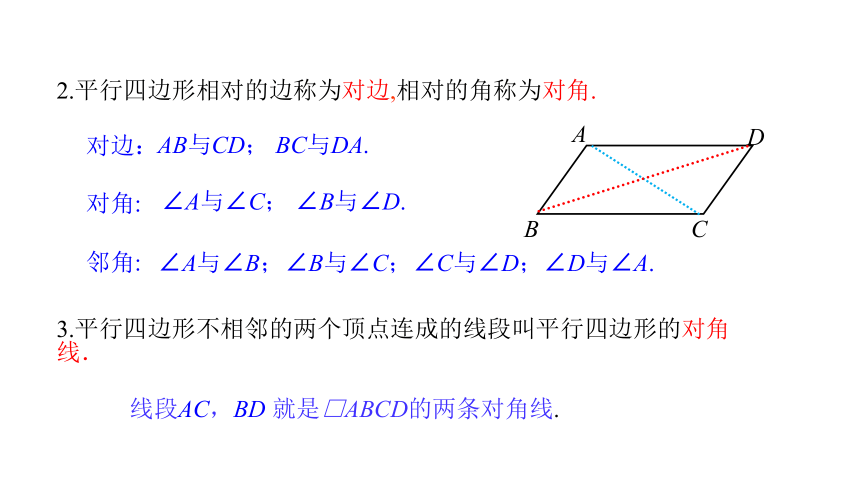
3.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
线段AC,BD 就是□ABCD的两条对角线.
A
D
C
B
2.平行四边形相对的边称为对边,相对的角称为对角.
对边:
对角:
邻角:
AB与CD; BC与DA.
∠A与∠C; ∠B与∠D.
∠A与∠B;∠B与∠C;∠C与∠D;∠D与∠A.
随 堂 练 习
1.
个
2.
个.
3
5
步骤:
(1)任意画一条直线m;
(2)在直线m上任取点A,在直线m外任取点B,连结AB;
(3)过点B作直线m的平行线n,在直线n上任取点C;
(4)过点C作直线AB的平行线,交直线m与点D,就得到□ABCD.
作一个平行四边形.
试一试
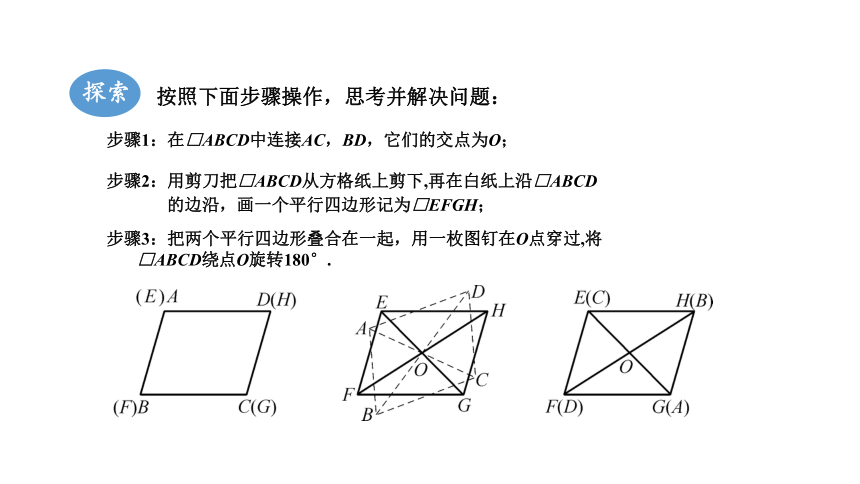
探索
步骤1:在□ABCD中连接AC,BD,它们的交点为O;
步骤3:把两个平行四边形叠合在一起,用一枚图钉在O点穿过,将
□ABCD绕点O旋转180°.
步骤2:用剪刀把□ABCD从方格纸上剪下,再在白纸上沿□ABCD
的边沿,画一个平行四边形记为□EFGH;
按照下面步骤操作,思考并解决问题:
思考以下问题:
(1)观察旋转后的□ABCD和画出来的□EFGH是否重合?平行四边形是什么样的对称图形?
(2)你能从中得出□ABCD的一些边、角关系吗?
平行四边形是中心对称图形,O是对称中心.
平行四边形的对边相等,对角相等
你能证明这些结论吗?
D
A
B
C
已知: 如图,□ABCD .
求证:AB=CD,AD=CB, ∠DAB= ∠DCB , ∠ADC= ∠ABC
证明:连结BD.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC,
∴ ∠ABD= ∠CDB, ∠ADB= ∠CBD.
∵ BD=DB,
∴ △ABD≌△CDB.
∴ AB=CD,AD=CB, ∠DAB= ∠DCB.
∵ ∠ABD= ∠CDB,∠ADB= ∠CBD,
∴ ∠ABD+ ∠CBD= ∠CDB + ∠ADB,
∴ ∠ABC= ∠ADC.
平行四边形问题可以转化为三角形问题来解决.
知 识 讲 解
知识点1 平行四边形的性质定理
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
几何语言:∵ 四边形ABCD是平行四边形,
∴ AD=BC ,AB=DC.
几何语言:∵ 四边形ABCD是平行四边形 ,
∴ ∠ A=∠C,∠ B=∠D.
B
A
D
C
例 1
例 题 精 讲
如图,在□ABCD中,∠A=40°,求其他各内角的大小.
B
C
D
A
解:在□ABCD中,
∴∠A =∠C,∠B=∠D(平行四边形的对角相等).
∵∠A=40°,
∴∠C=40°.
又∵AD∥BC,
∴∠A +∠B =180°.
∴∠B=180°-∠A=180°-140°= 140°,
∴∠D=∠B=140°.
平行四边形的邻角互补.
例 2
如图,在□ABCD中,AB=8,周长是24,求其余三条边的长.
解:在□ABCD中,
∴AB=DC,AD=BC(平行四边形的对边相等).
∵AB=8 ,
∴DC=8,
又∵AB+BC+CD+DA=24,
∴ AD=BC=4.
B
C
D
A
随 堂 练 习
B
C
D
A
30°
150°
150°
80°
100°
10 cm
12 cm2
如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.
试一试
你能发现什么结论?试用平行四边形的性质定理加以说明.
平行线之间的距离处处相等.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
随 堂 练 习
1.如图,如果直线l1//l2,那么△ABC的面积和△DBC的面积是相等的.你能说出理由吗 你还能在这两条平行线之间画出其他与△ABC面积相等的三角形吗
E
解:分别过点A,D作AM⊥l2,DN⊥l2.
∵l1//l2,
∴AM=DN(平行线之间的距离处处相等).
又∵S△ABC=BC·AM,S△DBC=BC·DN,
∴S△ABC=S△DBC.
M
N
A
D
C
B
l1
l2
如图,△EBC的面积等于△ABC的面积.(画法不一,只要两个三角形同底等高即可)
例 3
例 题 精 讲
C
D
A
B
已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解:如图,设AB的长为x,则BC的长为x +4.
根据已知,可得
2(AB + BC) = 24,
即 2(x +x +4) = 24,
4x+8=24,
解得 x=4.
所以,该平行四边形相邻两边的长分别为4和8.
例 4
B
C
D
A
E
已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE + BC = CD.
证明:∵四边形ABCD是平行四边形,
∴AB = CD (平行四边形的对边相等),
AB // CD (平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE =∠CDE,
∠ADE =∠AED,
∴ AD =AE.
又∵AD = BC(平行四边形的对边相等),
∴ AE= BC.
∴BE+BC=BE+AE=AB=CD.
随 堂 练 习
1.
4
2
4
2
2.如图:已知平行四边形ABCD周长等于16,AB:BC=3:5, 求平行四边形的各边长.
解:设AB=3x,则BC=5x,
在平行四边形ABCD中,
AB=CD=3x,AD=BC=5x,
(平行四边形的对边相等)
∵AB+CD+AD+BC=16,
∴3x+3x+5x+5x=16,
∴ x=1,
∴AB=CD=3,AD=BC=5.
当 堂 检 测
已知: □ABCD.
1.若AB+BC=10,则□ABCD的周长为 .
2.若∠A+∠C=100°,则∠B=____,∠C=____.
3.若AD∶CD =3∶4,周长是42,则AB=____,BC=____.
4.∠A:∠B=5:4,则∠C、∠D的度数分别为( )
A、100°和80° B、100°和50°
C、120°和60° D、135°和45°
20
130°
50°
12
9
A
5.如图,在平行四边形ABCD中, ∠B=120°,DE⊥AB,垂足为E,DF⊥BC,垂足为F.求∠ADE,∠EDF,∠FDC的度数.
解:在平行四边形ABCD中,
∠A+∠B= 180°,∠C+∠B=180°
(平行四边形的邻角互补).
∵∠B =120° ,
∴∠A= ∠C = 180°-120°=60°.
∵DE⊥AB,DF⊥BC,
∴∠ADE=90°-∠A =90°-60°=30°,
∠FDC=90°-∠A =90°-60°=30°,
∠EDF=180°-∠B =180°-120°=60°.
课 堂 小 结
平行
四边形
定义
两组对边分别平行的四边形
性质
平行四边形的对角相等
平行四边形是中心对称图形
平行四边形的对边相等
平行线之间的距离处处相等.
18.1 平行四边形的性质
第1课时 平行四边形的性质定理1、2
学 习 目 标
1.理解并掌握平行四边形的概念.
2.探索平行四边形的中心对称性质.
3.探索并证明平行四边形的性质定理:对边相等,对角相等.(重点)
4.灵活运用平行四边形的性质解决简单的平行四边形的计算、证明问题.(难点)
情 境 导 入
平行四边形是随处可见的几何图形.生活中,你还见过哪些平行四边形?用自己的语言描述一下什么样的图形叫做平行四边形.
回忆
你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
(6)
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
∴四边形ABCD是平行四边形
几何语言:
∵AB∥CD,AD∥BC
记作:□ABCD
3.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
线段AC,BD 就是□ABCD的两条对角线.
A
D
C
B
2.平行四边形相对的边称为对边,相对的角称为对角.
对边:
对角:
邻角:
AB与CD; BC与DA.
∠A与∠C; ∠B与∠D.
∠A与∠B;∠B与∠C;∠C与∠D;∠D与∠A.
随 堂 练 习
1.
个
2.
个.
3
5
步骤:
(1)任意画一条直线m;
(2)在直线m上任取点A,在直线m外任取点B,连结AB;
(3)过点B作直线m的平行线n,在直线n上任取点C;
(4)过点C作直线AB的平行线,交直线m与点D,就得到□ABCD.
作一个平行四边形.
试一试
探索
步骤1:在□ABCD中连接AC,BD,它们的交点为O;
步骤3:把两个平行四边形叠合在一起,用一枚图钉在O点穿过,将
□ABCD绕点O旋转180°.
步骤2:用剪刀把□ABCD从方格纸上剪下,再在白纸上沿□ABCD
的边沿,画一个平行四边形记为□EFGH;
按照下面步骤操作,思考并解决问题:
思考以下问题:
(1)观察旋转后的□ABCD和画出来的□EFGH是否重合?平行四边形是什么样的对称图形?
(2)你能从中得出□ABCD的一些边、角关系吗?
平行四边形是中心对称图形,O是对称中心.
平行四边形的对边相等,对角相等
你能证明这些结论吗?
D
A
B
C
已知: 如图,□ABCD .
求证:AB=CD,AD=CB, ∠DAB= ∠DCB , ∠ADC= ∠ABC
证明:连结BD.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC,
∴ ∠ABD= ∠CDB, ∠ADB= ∠CBD.
∵ BD=DB,
∴ △ABD≌△CDB.
∴ AB=CD,AD=CB, ∠DAB= ∠DCB.
∵ ∠ABD= ∠CDB,∠ADB= ∠CBD,
∴ ∠ABD+ ∠CBD= ∠CDB + ∠ADB,
∴ ∠ABC= ∠ADC.
平行四边形问题可以转化为三角形问题来解决.
知 识 讲 解
知识点1 平行四边形的性质定理
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
几何语言:∵ 四边形ABCD是平行四边形,
∴ AD=BC ,AB=DC.
几何语言:∵ 四边形ABCD是平行四边形 ,
∴ ∠ A=∠C,∠ B=∠D.
B
A
D
C
例 1
例 题 精 讲
如图,在□ABCD中,∠A=40°,求其他各内角的大小.
B
C
D
A
解:在□ABCD中,
∴∠A =∠C,∠B=∠D(平行四边形的对角相等).
∵∠A=40°,
∴∠C=40°.
又∵AD∥BC,
∴∠A +∠B =180°.
∴∠B=180°-∠A=180°-140°= 140°,
∴∠D=∠B=140°.
平行四边形的邻角互补.
例 2
如图,在□ABCD中,AB=8,周长是24,求其余三条边的长.
解:在□ABCD中,
∴AB=DC,AD=BC(平行四边形的对边相等).
∵AB=8 ,
∴DC=8,
又∵AB+BC+CD+DA=24,
∴ AD=BC=4.
B
C
D
A
随 堂 练 习
B
C
D
A
30°
150°
150°
80°
100°
10 cm
12 cm2
如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.
试一试
你能发现什么结论?试用平行四边形的性质定理加以说明.
平行线之间的距离处处相等.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
随 堂 练 习
1.如图,如果直线l1//l2,那么△ABC的面积和△DBC的面积是相等的.你能说出理由吗 你还能在这两条平行线之间画出其他与△ABC面积相等的三角形吗
E
解:分别过点A,D作AM⊥l2,DN⊥l2.
∵l1//l2,
∴AM=DN(平行线之间的距离处处相等).
又∵S△ABC=BC·AM,S△DBC=BC·DN,
∴S△ABC=S△DBC.
M
N
A
D
C
B
l1
l2
如图,△EBC的面积等于△ABC的面积.(画法不一,只要两个三角形同底等高即可)
例 3
例 题 精 讲
C
D
A
B
已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解:如图,设AB的长为x,则BC的长为x +4.
根据已知,可得
2(AB + BC) = 24,
即 2(x +x +4) = 24,
4x+8=24,
解得 x=4.
所以,该平行四边形相邻两边的长分别为4和8.
例 4
B
C
D
A
E
已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE + BC = CD.
证明:∵四边形ABCD是平行四边形,
∴AB = CD (平行四边形的对边相等),
AB // CD (平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE =∠CDE,
∠ADE =∠AED,
∴ AD =AE.
又∵AD = BC(平行四边形的对边相等),
∴ AE= BC.
∴BE+BC=BE+AE=AB=CD.
随 堂 练 习
1.
4
2
4
2
2.如图:已知平行四边形ABCD周长等于16,AB:BC=3:5, 求平行四边形的各边长.
解:设AB=3x,则BC=5x,
在平行四边形ABCD中,
AB=CD=3x,AD=BC=5x,
(平行四边形的对边相等)
∵AB+CD+AD+BC=16,
∴3x+3x+5x+5x=16,
∴ x=1,
∴AB=CD=3,AD=BC=5.
当 堂 检 测
已知: □ABCD.
1.若AB+BC=10,则□ABCD的周长为 .
2.若∠A+∠C=100°,则∠B=____,∠C=____.
3.若AD∶CD =3∶4,周长是42,则AB=____,BC=____.
4.∠A:∠B=5:4,则∠C、∠D的度数分别为( )
A、100°和80° B、100°和50°
C、120°和60° D、135°和45°
20
130°
50°
12
9
A
5.如图,在平行四边形ABCD中, ∠B=120°,DE⊥AB,垂足为E,DF⊥BC,垂足为F.求∠ADE,∠EDF,∠FDC的度数.
解:在平行四边形ABCD中,
∠A+∠B= 180°,∠C+∠B=180°
(平行四边形的邻角互补).
∵∠B =120° ,
∴∠A= ∠C = 180°-120°=60°.
∵DE⊥AB,DF⊥BC,
∴∠ADE=90°-∠A =90°-60°=30°,
∠FDC=90°-∠A =90°-60°=30°,
∠EDF=180°-∠B =180°-120°=60°.
课 堂 小 结
平行
四边形
定义
两组对边分别平行的四边形
性质
平行四边形的对角相等
平行四边形是中心对称图形
平行四边形的对边相等
平行线之间的距离处处相等.
