18.1 平行四边形的性质 第2课时 课件 (共19张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 18.1 平行四边形的性质 第2课时 课件 (共19张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
18.1 平行四边形的性质
第2课时 平行四边形的性质定理3
学 习 目 标
1.理解并掌握平行四边形的性质定理3.(重点)
2.运用平行四边形的性质定理3解决与对角线有关的计算、证明.(难点)
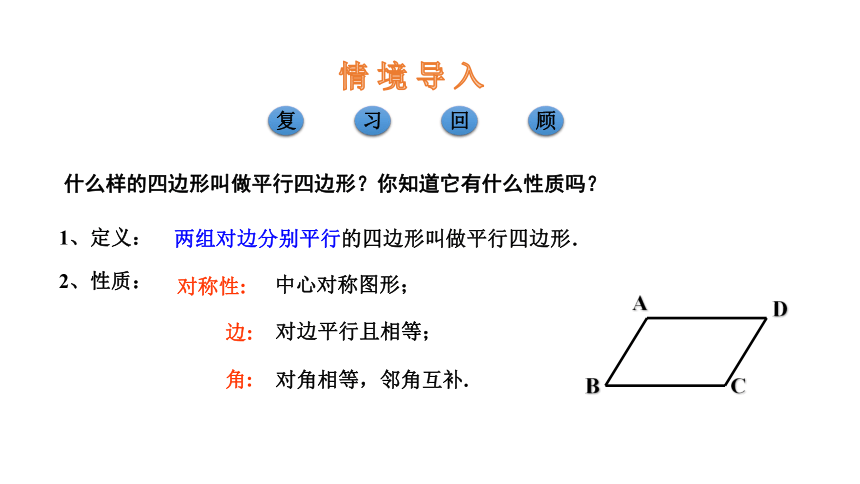
情 境 导 入
复
习
回
顾
A
D
B
C
1、定义:
两组对边分别平行的四边形叫做平行四边形.
边:
对边平行且相等;
角:
对角相等,邻角互补.
中心对称图形;
对称性:
2、性质:
什么样的四边形叫做平行四边形?你知道它有什么性质吗?
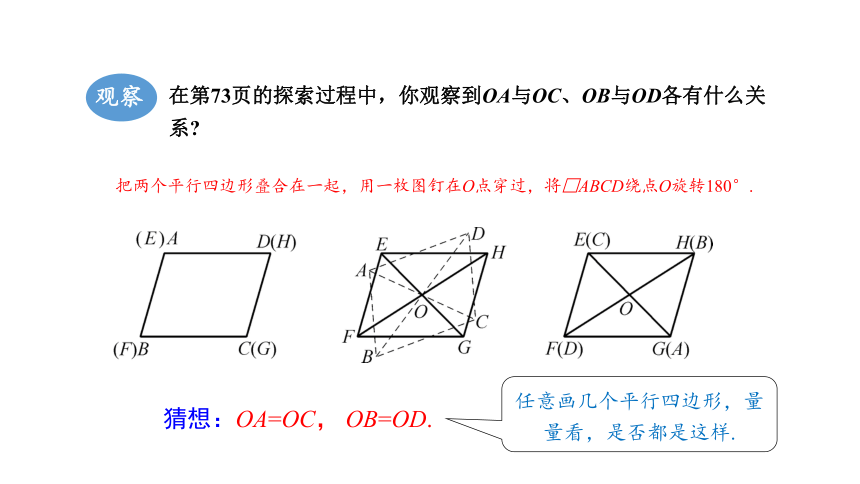
把两个平行四边形叠合在一起,用一枚图钉在O点穿过,将□ABCD绕点O旋转180°.
在第73页的探索过程中,你观察到OA与OC、OB与OD各有什么关系
观察
猜想:OA=OC, OB=OD.
任意画几个平行四边形,量量看,是否都是这样.
知 识 讲 解
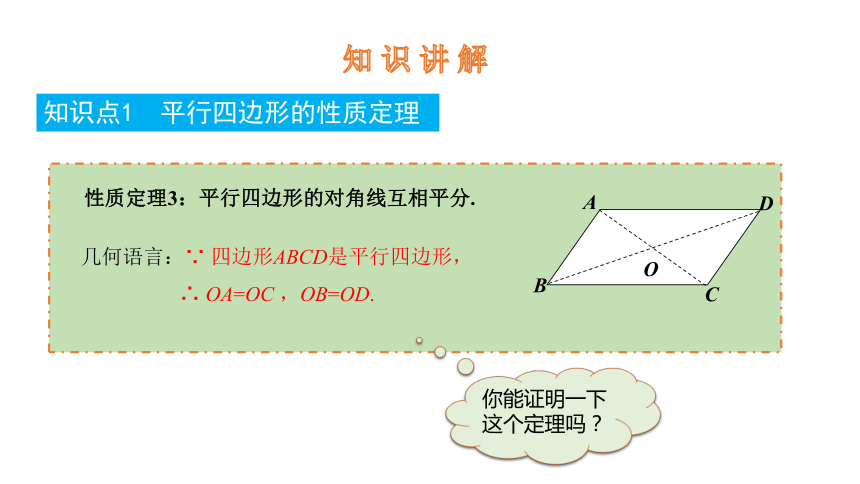
知识点1 平行四边形的性质定理
性质定理3:平行四边形的对角线互相平分.
几何语言:∵ 四边形ABCD是平行四边形,
∴ OA=OC ,OB=OD.
B
A
D
C
O
你能证明一下这个定理吗?
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
例 5
例 题 精 讲
如图, ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
解:在 ABCD中,
∵AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD(平行四边形的对角线互相平分),
∴AC+BD=2AO+2BO=2(AO+BO)=2×9=18.
例 6
如图, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
改变直线EF的位置,OE=OF还成立吗
成立
想一想
如图,在上述问题中,若直线EF与边AB,CD的延长线交于点E,F,上述结论是否仍然成立?试说明理由.
A
D
C
B
O
E
F
结论仍然成立.理由:
∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE, ∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD,OD=OB,
∴OE=OF.
过平行四边形对角线的交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
随 堂 练 习
1. 如图, ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.OB=OD D.AO⊥AB
C
2.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OAD的周长为( )
A.26 B.34 C.40 D.52
B
例 7
例 题 精 讲
如图, ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解:∵四边形ABCD是平行四边形,
∴OA = OC(平行四边形的对角线互相平分).
∵△AOB的周长+2=△BOC的周长,
∴AB+OA+OB+2=BC+OB+OC,
即AB +2 = BC.
又∵ ABCD的周长等于16,
∴2(AB + BC) = 16,
即4AB +4 = 16.
∴AB=3,BC=5.
例 8
如图,在 ABCD中,对角线AC=21 cm,BE⊥AC,垂足为点E,且BE = 5cm, AD = 7 cm.求AD和BC之间的距离.
解:设AD和BC之间的距离为x,则 ABCD的
面积等于AD·x.
∵S ABCD= 2S△ABC= AC· BE,
∴AD·x=AC·BE,
即7x = 21 ×5,
x= 15(cm).
即AD和BC之间的距离为15cm.
随 堂 练 习
1.如图, □ ABCD 的周长为60cm,对角线AC,BD相交于点O,三角形AOB的周长比三角形BOC的周长长8cm,求这个四边形各边长?
A
B
D
C
O
解: ∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边平行).
AO = CO,BO = DO (平行四边形的对角线互相平分).
∵AB + BC + CD + DA = 60,
(BC + BO + CO)-(AB + AO + BO)= 8,
∴ AB + BC =30,BC-AB = 8,
解得BC =19,AB =11.
当 堂 检 测
1.在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是( )
A. 24C.7B
C
D
A
O
C
2.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则OA的长是 .
2
3. 如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为____.
12
4.如图,在□ ABCD 中,已知对角线AC和BD相交于点O,三角形AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
A
D
B
C
解:在□ ABCD 中,已知AB=6,
AO+BO=15-6=9,
又因为AO=OC,BO=OD,(平行四边形对角线互相平分)
所以AC+BD=2AO+2BO
=2(AO+BO)
=2×9=18.
O
D
B
A
C
5.如图,在□ABCD中,对角线AC,BD相交于点O,且AC+BD=20,△AOB的周长等于15,求CD.
解: ∵四边形ABCD是平行四边形,
∴AB = CD(平行四边形的对边平行).
AO =AC, BO = BD(平行四边形的对角
线互相平分)
∵AB + BO + AO=15,
∴AB+AC+ BD =15,
∴AB+(AC+ BD )=15,
∵ AC+BD=20
∴AB+×20=15, 解得AB =5
∴ CD=AB=5.
课 堂 小 结
平行四边形对角线的性质
平行四边形对角线互相平分
拓展:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
18.1 平行四边形的性质
第2课时 平行四边形的性质定理3
学 习 目 标
1.理解并掌握平行四边形的性质定理3.(重点)
2.运用平行四边形的性质定理3解决与对角线有关的计算、证明.(难点)
情 境 导 入
复
习
回
顾
A
D
B
C
1、定义:
两组对边分别平行的四边形叫做平行四边形.
边:
对边平行且相等;
角:
对角相等,邻角互补.
中心对称图形;
对称性:
2、性质:
什么样的四边形叫做平行四边形?你知道它有什么性质吗?
把两个平行四边形叠合在一起,用一枚图钉在O点穿过,将□ABCD绕点O旋转180°.
在第73页的探索过程中,你观察到OA与OC、OB与OD各有什么关系
观察
猜想:OA=OC, OB=OD.
任意画几个平行四边形,量量看,是否都是这样.
知 识 讲 解
知识点1 平行四边形的性质定理
性质定理3:平行四边形的对角线互相平分.
几何语言:∵ 四边形ABCD是平行四边形,
∴ OA=OC ,OB=OD.
B
A
D
C
O
你能证明一下这个定理吗?
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
例 5
例 题 精 讲
如图, ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
解:在 ABCD中,
∵AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD(平行四边形的对角线互相平分),
∴AC+BD=2AO+2BO=2(AO+BO)=2×9=18.
例 6
如图, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
改变直线EF的位置,OE=OF还成立吗
成立
想一想
如图,在上述问题中,若直线EF与边AB,CD的延长线交于点E,F,上述结论是否仍然成立?试说明理由.
A
D
C
B
O
E
F
结论仍然成立.理由:
∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE, ∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD,OD=OB,
∴OE=OF.
过平行四边形对角线的交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
随 堂 练 习
1. 如图, ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.OB=OD D.AO⊥AB
C
2.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OAD的周长为( )
A.26 B.34 C.40 D.52
B
例 7
例 题 精 讲
如图, ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解:∵四边形ABCD是平行四边形,
∴OA = OC(平行四边形的对角线互相平分).
∵△AOB的周长+2=△BOC的周长,
∴AB+OA+OB+2=BC+OB+OC,
即AB +2 = BC.
又∵ ABCD的周长等于16,
∴2(AB + BC) = 16,
即4AB +4 = 16.
∴AB=3,BC=5.
例 8
如图,在 ABCD中,对角线AC=21 cm,BE⊥AC,垂足为点E,且BE = 5cm, AD = 7 cm.求AD和BC之间的距离.
解:设AD和BC之间的距离为x,则 ABCD的
面积等于AD·x.
∵S ABCD= 2S△ABC= AC· BE,
∴AD·x=AC·BE,
即7x = 21 ×5,
x= 15(cm).
即AD和BC之间的距离为15cm.
随 堂 练 习
1.如图, □ ABCD 的周长为60cm,对角线AC,BD相交于点O,三角形AOB的周长比三角形BOC的周长长8cm,求这个四边形各边长?
A
B
D
C
O
解: ∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边平行).
AO = CO,BO = DO (平行四边形的对角线互相平分).
∵AB + BC + CD + DA = 60,
(BC + BO + CO)-(AB + AO + BO)= 8,
∴ AB + BC =30,BC-AB = 8,
解得BC =19,AB =11.
当 堂 检 测
1.在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是( )
A. 24
C
D
A
O
C
2.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则OA的长是 .
2
3. 如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为____.
12
4.如图,在□ ABCD 中,已知对角线AC和BD相交于点O,三角形AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
A
D
B
C
解:在□ ABCD 中,已知AB=6,
AO+BO=15-6=9,
又因为AO=OC,BO=OD,(平行四边形对角线互相平分)
所以AC+BD=2AO+2BO
=2(AO+BO)
=2×9=18.
O
D
B
A
C
5.如图,在□ABCD中,对角线AC,BD相交于点O,且AC+BD=20,△AOB的周长等于15,求CD.
解: ∵四边形ABCD是平行四边形,
∴AB = CD(平行四边形的对边平行).
AO =AC, BO = BD(平行四边形的对角
线互相平分)
∵AB + BO + AO=15,
∴AB+AC+ BD =15,
∴AB+(AC+ BD )=15,
∵ AC+BD=20
∴AB+×20=15, 解得AB =5
∴ CD=AB=5.
课 堂 小 结
平行四边形对角线的性质
平行四边形对角线互相平分
拓展:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
