18.2 平行四边形的判定 第1课时 课件 (共20张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 18.2 平行四边形的判定 第1课时 课件 (共20张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
18.2 平行四边形的判定
第1课时 平行四边形的判定定理1、2
学 习 目 标
1.经历平行四边形判定定理的动手操作与证明过程,体会类比思想及探究图形判定的一般思路.(重点)
2.掌握平行四边形定义判定和判定定理1,2,能根据不同条件灵活选取适当的判定定理进行推理论证.(难点)
情 境 导 入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
只要使互相平行的夹在铁轨之间的枕木长度相等就可以了
那这是为什么呢?会不会跟我们学过的平行四边形有关呢?
把四根小棒首尾顺次相接,围成一个四边形,观察四边形具备什么条件?是否是平行四边形?为什么?
探究1
小组内展示一下你拼出来的图形.
里面有平行四边形吗?你能证明一下吗?
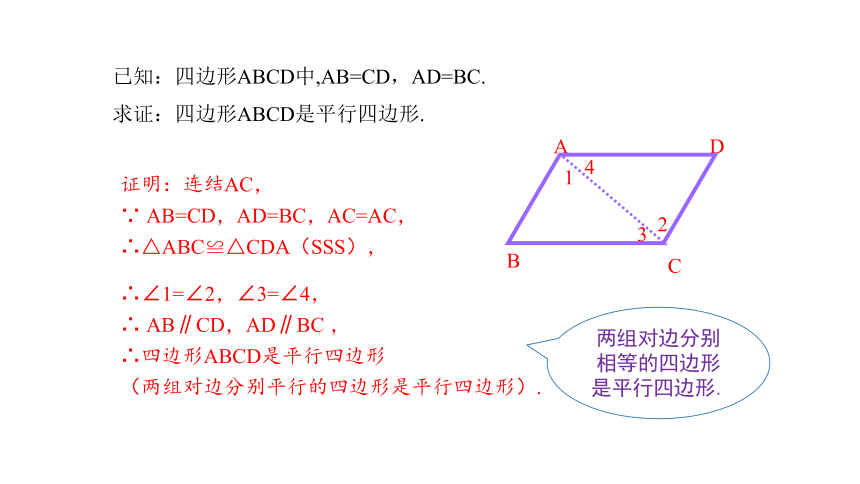
已知:四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
B
D
A
C
2
1
3
4
证明:连结AC,
∵ AB=CD,AD=BC,AC=AC,
∴△ABC≌△CDA(SSS),
∴∠1=∠2,∠3=∠4,
∴ AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形).
两组对边分别相等的四边形是平行四边形.
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想1:一组对边相等的四边形是平行四边形吗?
等腰梯形不是平行四边形,因而此猜想错误.
猜想2:一组对边平行的四边形是平行四边形吗?
梯形的上下底平行,但不是平行四边形,因而此猜想错误
探究2
B
A
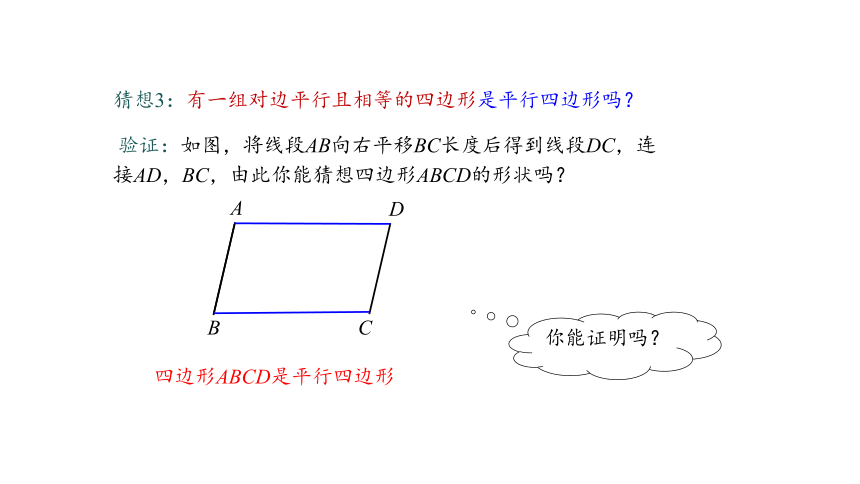
验证:如图,将线段AB向右平移BC长度后得到线段DC,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
你能证明吗?
猜想3:有一组对边平行且相等的四边形是平行四边形吗?
A
B
C
D
证明思路
作对角线构造全等三角形
一组对应边平行且相等
1、两组对边分别相等
2、两组对边分别平行
四边形ABCD是平行四边形
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:有一组对边平行且相等的四边形是平行四边形
知 识 讲 解
知识点1 平行四边形的判定定理
两组对边分别相等的四边形是平行四边形.
∵在四边形ABCD中,
AB=CD,AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1:
B
D
C
A
知 识 讲 解
知识点1 平行四边形的判定定理
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AD∥BC,AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2:
B
D
C
A
例 1
例 题 精 讲
证明:∵四边形 ABCD 是平行四边形,
∴AD∥CB(平行四边形的对边平行),
即AF∥CE.
又∵AF =CE,
∴四边形 AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形).
如图 ,在平行四边形 ABCD 中,点E,F 分别在对边BC和DA 上,且AF=CE.求证:四边形 AECF是平行四边形.
还可以用其他方法证明例1吗?
方法2:∵四边形 ABCD 是平行四边形,
∴AB=CD,AD=BC(平行四边形的对边相等),
∠B=∠D(平行四边形的对角相等).
又∵AF =CE,
∴AD-AF=BC-CE,即FD=BE.
∴△ABE≌△CDF(SAS).
∴AE=CF.
∴四边形 AECF 是平行四边形(两组对边分别相等的四边形是平行四边形).
如图 ,在平行四边形 ABCD 中,点E,F 分别在对边BC和DA 上,且AF=CE.求证:四边形 AECF是平行四边形.
试试能不能用定义来证明?哪种方法较为简捷?
随 堂 练 习
1、已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是( )
A.AB∥CD,AB=CD
B.AB∥CD,AD∥BC
C.AB∥CD,AB=BC
D.AB=CD,AD=BC
C
证明:∵ △ABC ≌ △CDA,
∴ AB = CD, BC = DA.
∴ 四边形 ABCD 是平行四边形
2.如图,在四边形ABCD中,△ABC ≌△ CDA.
求证:四边形 ABCD 是平行四边形.
当 堂 检 测
1. 如图所示,△ABC 是等边三角形,P 是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC 的周长为 24,则 PD + PE + PF = .
A
F
B
D
C
E
P
8
2.已知 AD∥BC ,要使这个四边形 ABCD 为平行四边形,需要增加条件 .
AD = BC 或 AB∥CD
∵E,F 分别是 AD,BC 的中点,
3. 已知:如图,E,F 分别是平行四边形 ABCD 的边 AD,BC 的中点.求证:BE = DF.
D
F
E
C
B
A
证明:
∵四边形 ABCD 是平行四边形,
∴AD∥BC,AD = BC.
∴ED = BF,即 ED BF.
∥
=
∴四边形 EBFD 是平行四边形(一组对边平行并且相等的四边形是平行四边形).
∴BE = DF (平行四边形的对边分别相等).
证明:在平行四边形 ABCD 中,∠A = ∠C,AD = BC,
又∵BF = DH,
∴AH = CF.
又∵AE = CG,
∴△AEH≌△CGF(SAS).
∴EH = GF.
同理得△BEF≌△DGH(S.A.S.)∴GH = EF.
∴四边形 EFGH 是平行四边形.
4. 如图,已知 E,F,G,H 分别是□ABCD 的边 AB,BC,CD,DA 上的点,且 AE = CG,BF = DH.求证:四边形 EFGH 是平行四边形.
课 堂 小 结
平行四边形的判定
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
18.2 平行四边形的判定
第1课时 平行四边形的判定定理1、2
学 习 目 标
1.经历平行四边形判定定理的动手操作与证明过程,体会类比思想及探究图形判定的一般思路.(重点)
2.掌握平行四边形定义判定和判定定理1,2,能根据不同条件灵活选取适当的判定定理进行推理论证.(难点)
情 境 导 入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
只要使互相平行的夹在铁轨之间的枕木长度相等就可以了
那这是为什么呢?会不会跟我们学过的平行四边形有关呢?
把四根小棒首尾顺次相接,围成一个四边形,观察四边形具备什么条件?是否是平行四边形?为什么?
探究1
小组内展示一下你拼出来的图形.
里面有平行四边形吗?你能证明一下吗?
已知:四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
B
D
A
C
2
1
3
4
证明:连结AC,
∵ AB=CD,AD=BC,AC=AC,
∴△ABC≌△CDA(SSS),
∴∠1=∠2,∠3=∠4,
∴ AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形).
两组对边分别相等的四边形是平行四边形.
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想1:一组对边相等的四边形是平行四边形吗?
等腰梯形不是平行四边形,因而此猜想错误.
猜想2:一组对边平行的四边形是平行四边形吗?
梯形的上下底平行,但不是平行四边形,因而此猜想错误
探究2
B
A
验证:如图,将线段AB向右平移BC长度后得到线段DC,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
你能证明吗?
猜想3:有一组对边平行且相等的四边形是平行四边形吗?
A
B
C
D
证明思路
作对角线构造全等三角形
一组对应边平行且相等
1、两组对边分别相等
2、两组对边分别平行
四边形ABCD是平行四边形
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:有一组对边平行且相等的四边形是平行四边形
知 识 讲 解
知识点1 平行四边形的判定定理
两组对边分别相等的四边形是平行四边形.
∵在四边形ABCD中,
AB=CD,AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1:
B
D
C
A
知 识 讲 解
知识点1 平行四边形的判定定理
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AD∥BC,AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2:
B
D
C
A
例 1
例 题 精 讲
证明:∵四边形 ABCD 是平行四边形,
∴AD∥CB(平行四边形的对边平行),
即AF∥CE.
又∵AF =CE,
∴四边形 AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形).
如图 ,在平行四边形 ABCD 中,点E,F 分别在对边BC和DA 上,且AF=CE.求证:四边形 AECF是平行四边形.
还可以用其他方法证明例1吗?
方法2:∵四边形 ABCD 是平行四边形,
∴AB=CD,AD=BC(平行四边形的对边相等),
∠B=∠D(平行四边形的对角相等).
又∵AF =CE,
∴AD-AF=BC-CE,即FD=BE.
∴△ABE≌△CDF(SAS).
∴AE=CF.
∴四边形 AECF 是平行四边形(两组对边分别相等的四边形是平行四边形).
如图 ,在平行四边形 ABCD 中,点E,F 分别在对边BC和DA 上,且AF=CE.求证:四边形 AECF是平行四边形.
试试能不能用定义来证明?哪种方法较为简捷?
随 堂 练 习
1、已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是( )
A.AB∥CD,AB=CD
B.AB∥CD,AD∥BC
C.AB∥CD,AB=BC
D.AB=CD,AD=BC
C
证明:∵ △ABC ≌ △CDA,
∴ AB = CD, BC = DA.
∴ 四边形 ABCD 是平行四边形
2.如图,在四边形ABCD中,△ABC ≌△ CDA.
求证:四边形 ABCD 是平行四边形.
当 堂 检 测
1. 如图所示,△ABC 是等边三角形,P 是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC 的周长为 24,则 PD + PE + PF = .
A
F
B
D
C
E
P
8
2.已知 AD∥BC ,要使这个四边形 ABCD 为平行四边形,需要增加条件 .
AD = BC 或 AB∥CD
∵E,F 分别是 AD,BC 的中点,
3. 已知:如图,E,F 分别是平行四边形 ABCD 的边 AD,BC 的中点.求证:BE = DF.
D
F
E
C
B
A
证明:
∵四边形 ABCD 是平行四边形,
∴AD∥BC,AD = BC.
∴ED = BF,即 ED BF.
∥
=
∴四边形 EBFD 是平行四边形(一组对边平行并且相等的四边形是平行四边形).
∴BE = DF (平行四边形的对边分别相等).
证明:在平行四边形 ABCD 中,∠A = ∠C,AD = BC,
又∵BF = DH,
∴AH = CF.
又∵AE = CG,
∴△AEH≌△CGF(SAS).
∴EH = GF.
同理得△BEF≌△DGH(S.A.S.)∴GH = EF.
∴四边形 EFGH 是平行四边形.
4. 如图,已知 E,F,G,H 分别是□ABCD 的边 AB,BC,CD,DA 上的点,且 AE = CG,BF = DH.求证:四边形 EFGH 是平行四边形.
课 堂 小 结
平行四边形的判定
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
