20.2 数据的集中趋势 第1课时 课件 (共23张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 20.2 数据的集中趋势 第1课时 课件 (共23张PPT) 2023-2024学年数学华师版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 20:53:44 | ||
图片预览






文档简介
(共23张PPT)
20.2 数据的集中趋势
第1课时 中位数和众数
学 习 目 标
1.理解数据的中位数和众数的概念.
2.会求一组数据的中位数和众数.(重点)
3.能利用中位数、众数分析数据信息做出决策.(难点)
情 境 导 入
第二天,小王上班了.
职员D
我的工资是4 000元,在公司算中等收入
我这里报酬不错,月平均工资是6 000元,你在这儿好好干!
你们公司员工收入到底怎样呢?
我们好几个人工资都是3 000元.
应聘者小王
经理
职员C
小王在公司工作了一周后……
你欺骗了我,我已问过其他职员,没有几个职员的工资超过 6000 元.
平均工资确实是每月 6000 元,你看看公司的工资报表.
应聘者小王
经理
日常生活中,我们面对一组数据,常常需要寻找一个表达这组数据总体面貌的代表:
(1)同学问小明:“你知道你妈妈的鞋号是多少码 ”小明在家里找到了9双妈妈的鞋,鞋号分别是:23,23,23,23.5,23,24,23,23,24.他的回答应该是 .
想一想
23
(2)同学问小红:“你每个月有多少零花钱 ”小红查了自己的记账本,发现去年每月得到的零花钱(单位:元)分别是:500,100,100,100,100,150,100,200,100,100,100,100.她的回答可以是 ;
(3)老师要评定每位学生的中文打字速度.李兵的三次中文打字速度检测结果(单位:字/分钟)分别是38,31,36,他的中文打字速度可评定为 ;
100
36
(4)一家小店有5名从业者,他们的月收入(单位:元)分别:8000,3200,2100,
2000,2000,该店员工的月收入可以认为是 .
2100
以上几组数的选择有什么特点?
(1)23,23,23,23.5,23,24,23,23,24
23
(2)500,100,100,100,100,150,100,200,100,100,100,100
100
(3)38,31,36
(4)8000,3200,2100,2000,2000
36
2100
出现次数最多:众数
按大小顺序排列在最中间:中位数
除了平均数之外,我们还用中位数和众数来刻画数据的集中趋势.
问题
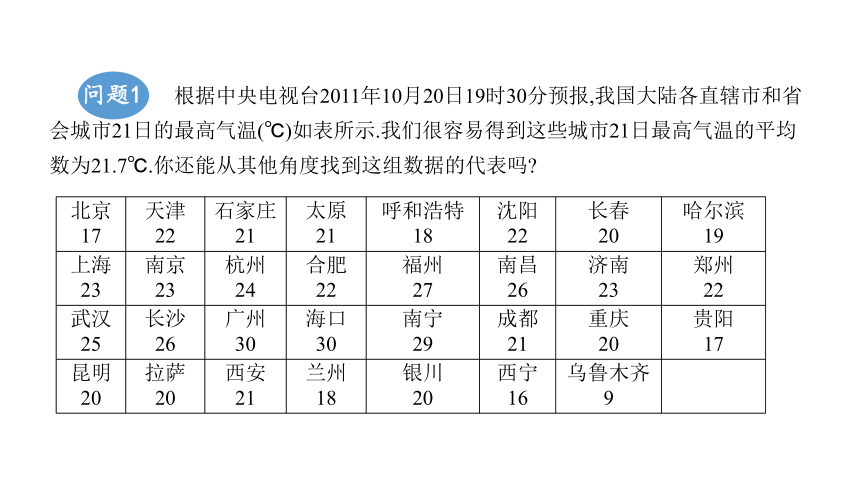
根据中央电视台2011年10月20日19时30分预报,我国大陆各直辖市和省会城市21日的最高气温(℃)如表所示.我们很容易得到这些城市21日最高气温的平均数为21.7℃.你还能从其他角度找到这组数据的代表吗
北京 17 天津 22 石家庄 21 太原 21 呼和浩特 18 沈阳 22 长春 20 哈尔滨
19
上海 23 南京 23 杭州 24 合肥 22 福州 27 南昌 26 济南 23 郑州
22
武汉 25 长沙 26 广州 30 海口 30 南宁 29 成都 21 重庆 20 贵阳
17
昆明 20 拉萨 20 西安 21 兰州 18 银川 20 西宁 16 乌鲁木齐 9
问题1
(1)如何用中位数来做这组数据的代表?
9 16 17 17 18 18 19 20 20 20 20 20 21 21 21 21 22 22 22 22 23 23 23 24 25 26 26 27 29 30 30
①将整组数据按升序排列;
②找到整组数据居于最中间的数;
用依次去掉两端逐步接近正中心的方法
21℃位于整组31个数据从小到大排序的第16位,即为31/2=15.5向上取整的位数上.
9 16 17 17 18 18 19 20 20 20 20 20 21 21 21 21 22 22 22 22 23 23 23 24 25 26 26 27 29 30 30
如果去掉一个数据,使整组数据个数为偶数个时,如何找到中位数?
如果用依次去掉两端逐步接近正中心的方法,发现中间没有数了,此时没有中位数吗?或者可以取21℃或22℃吗?
当整组数据个数为偶数个时,为了公平起见,我们会取最中间两个数的平均数作为中位数.
思考
(2)如何用众数来做这组数据的代表?
①找到每个数据出现的频数;
气温(℃) 9 16 17 18 19 20 21 22 23 24 25 26 27 29 30
频数 1 1 2 2 1 5 4 4 3 1 1 2 1 1 2
②找到频数最大的数据20℃,即为这组数据的众数.
9 16 17 17 18 18 19 20 20 20 20 20 21 21 21 21 22 22 22 22 23 23 23 24 25 26 26 27 29 30 30
若有两个气温值(如20℃和22℃)的频数并列最多,那么怎样确定众数呢?
与中位数不同,此时我们不是取20℃和22℃这两个数的平均数作为众数,而是说这两个气温值都是众数.
若每气温值都只出现一次,那么怎样确定众数呢?
此时没有众数.
思考
我们可以把问题1中的平均数、中位数和众数在统计图上表示出来.
频数
温度(℃)
众数
(20)
中位数
(21)
平均数
(21.7)
探究
知 识 讲 解
知识点 中位数与众数
问题1
②如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半,反映了一组数据的中间水平.
1、中位数的特征及意义:
①如果将一组数据按由小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
知 识 讲 解
知识点 中位数与众数
问题1
②一组数据的众数一定出现在这组数据中;
①众数是一组数据中出现次数最多的数据;
③一组数据可能有多个众数,也可能没有众数,众数反映了一组数据的多数水平.
2、众数的特征及意义:
例 1
例 题 精 讲
某商场进了一批苹果,每箱苹果的质量约为5千克.进入仓库前,从中随机抽出10箱称重,得到10箱苹果的质量如下:(单位:千克)
4.8,5.0, 5.1, 4.8, 4.9,4.8, 5.1, 4.9, 4.7, 4.7
请指出这10箱苹果质量的平均数、中位数和众数.
解:这10箱苹果质量的平均数为:
中位数为:4.85(千克);众数为:4.8(千克)
1.判断题(对的在括号内填“√”,错的在括号内填“×”)
(1)给定一组数据,那么这组数据的平均数一定只有一个. ( )
(2)给定一组数据,那么这组数据的中位数一定只有一个. ( )
(3)给定一组数据,那么这组数据的众数一定只有一个. ( )
(4)给定一组数据,那么这组数据的平均数一定位于最大值和最小值之间. ( )
(5)给定一组数据,那么这组数据的中位数一定等于最小值和最大值的平均数. ( )
(6)给定一组数据,如果找不到众数,那么众数一定就是 0. ( )
√
√
×
√
×
×
随 堂 练 习
2.一名警察在高速公路上随机观察了 6 辆过往车辆,它们的速度(单位: 千米/ 时)分别为: 66, 57, 71, 54, 69, 58. 那么,这 6 辆车的速度的中位数和众数分别是多少
解:这 6 辆车的速度的中位数为:62(千米/ 时)
这 6 辆车的速度的没有众数.
当 堂 检 测
1.数据 1,2, 8,5,3,9,5,4,5,4 的众数、中位数分别为( )
A.4.5、5 B.5、4.5 C.5、4 D.5、5
2.要调查多数同学们喜欢看的电视节目,应关注的是哪个数据的代表( )
A.平均数 B.中位数 C.众数
3.在演讲比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A.平均数 B.中位数 C.众数
B
C
B
4.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班 50 名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数 2 2 6 12 13 4 3
(1)填写图表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
2.44
(3)这组数据的中位数是 ,众数是 .
2.5
3
8
5.某校男子足球队的年龄分布如下面的条形图所示.请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
人数
13
14
15
16
17
18
年龄/岁
0
2
4
6
8
10
解:这些队员年龄的平均数为:(13×2+14×6+15×8+16×3+17×2+18×1)÷22 = 15,
队员年龄的众数为 15,队员年龄的中位数是 15.
意义:由平均数是 15 可说明
队员们的平均年龄为 15;
由众数是 15 可说明
大多数队员的年龄为 15 岁;
由中位数是 15 可说明有一半队员的年龄大于或等于 15 岁,有一半队员的年龄小于或等于 15 岁.
课 堂 小 结
中位数与
众数
中位数:表示一组数据的中间水平,中位数左右的数据一样多.
众数:表示一组数据的多数水平,众数可能有多个,也可能没有众数.
中位数求法三步:排序—判断(个数是奇还是偶)—确定或算出.
课 后 作 业
1.从课后习题中选取;
2.完成练习册本课时的习题.
20.2 数据的集中趋势
第1课时 中位数和众数
学 习 目 标
1.理解数据的中位数和众数的概念.
2.会求一组数据的中位数和众数.(重点)
3.能利用中位数、众数分析数据信息做出决策.(难点)
情 境 导 入
第二天,小王上班了.
职员D
我的工资是4 000元,在公司算中等收入
我这里报酬不错,月平均工资是6 000元,你在这儿好好干!
你们公司员工收入到底怎样呢?
我们好几个人工资都是3 000元.
应聘者小王
经理
职员C
小王在公司工作了一周后……
你欺骗了我,我已问过其他职员,没有几个职员的工资超过 6000 元.
平均工资确实是每月 6000 元,你看看公司的工资报表.
应聘者小王
经理
日常生活中,我们面对一组数据,常常需要寻找一个表达这组数据总体面貌的代表:
(1)同学问小明:“你知道你妈妈的鞋号是多少码 ”小明在家里找到了9双妈妈的鞋,鞋号分别是:23,23,23,23.5,23,24,23,23,24.他的回答应该是 .
想一想
23
(2)同学问小红:“你每个月有多少零花钱 ”小红查了自己的记账本,发现去年每月得到的零花钱(单位:元)分别是:500,100,100,100,100,150,100,200,100,100,100,100.她的回答可以是 ;
(3)老师要评定每位学生的中文打字速度.李兵的三次中文打字速度检测结果(单位:字/分钟)分别是38,31,36,他的中文打字速度可评定为 ;
100
36
(4)一家小店有5名从业者,他们的月收入(单位:元)分别:8000,3200,2100,
2000,2000,该店员工的月收入可以认为是 .
2100
以上几组数的选择有什么特点?
(1)23,23,23,23.5,23,24,23,23,24
23
(2)500,100,100,100,100,150,100,200,100,100,100,100
100
(3)38,31,36
(4)8000,3200,2100,2000,2000
36
2100
出现次数最多:众数
按大小顺序排列在最中间:中位数
除了平均数之外,我们还用中位数和众数来刻画数据的集中趋势.
问题
根据中央电视台2011年10月20日19时30分预报,我国大陆各直辖市和省会城市21日的最高气温(℃)如表所示.我们很容易得到这些城市21日最高气温的平均数为21.7℃.你还能从其他角度找到这组数据的代表吗
北京 17 天津 22 石家庄 21 太原 21 呼和浩特 18 沈阳 22 长春 20 哈尔滨
19
上海 23 南京 23 杭州 24 合肥 22 福州 27 南昌 26 济南 23 郑州
22
武汉 25 长沙 26 广州 30 海口 30 南宁 29 成都 21 重庆 20 贵阳
17
昆明 20 拉萨 20 西安 21 兰州 18 银川 20 西宁 16 乌鲁木齐 9
问题1
(1)如何用中位数来做这组数据的代表?
9 16 17 17 18 18 19 20 20 20 20 20 21 21 21 21 22 22 22 22 23 23 23 24 25 26 26 27 29 30 30
①将整组数据按升序排列;
②找到整组数据居于最中间的数;
用依次去掉两端逐步接近正中心的方法
21℃位于整组31个数据从小到大排序的第16位,即为31/2=15.5向上取整的位数上.
9 16 17 17 18 18 19 20 20 20 20 20 21 21 21 21 22 22 22 22 23 23 23 24 25 26 26 27 29 30 30
如果去掉一个数据,使整组数据个数为偶数个时,如何找到中位数?
如果用依次去掉两端逐步接近正中心的方法,发现中间没有数了,此时没有中位数吗?或者可以取21℃或22℃吗?
当整组数据个数为偶数个时,为了公平起见,我们会取最中间两个数的平均数作为中位数.
思考
(2)如何用众数来做这组数据的代表?
①找到每个数据出现的频数;
气温(℃) 9 16 17 18 19 20 21 22 23 24 25 26 27 29 30
频数 1 1 2 2 1 5 4 4 3 1 1 2 1 1 2
②找到频数最大的数据20℃,即为这组数据的众数.
9 16 17 17 18 18 19 20 20 20 20 20 21 21 21 21 22 22 22 22 23 23 23 24 25 26 26 27 29 30 30
若有两个气温值(如20℃和22℃)的频数并列最多,那么怎样确定众数呢?
与中位数不同,此时我们不是取20℃和22℃这两个数的平均数作为众数,而是说这两个气温值都是众数.
若每气温值都只出现一次,那么怎样确定众数呢?
此时没有众数.
思考
我们可以把问题1中的平均数、中位数和众数在统计图上表示出来.
频数
温度(℃)
众数
(20)
中位数
(21)
平均数
(21.7)
探究
知 识 讲 解
知识点 中位数与众数
问题1
②如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半,反映了一组数据的中间水平.
1、中位数的特征及意义:
①如果将一组数据按由小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
知 识 讲 解
知识点 中位数与众数
问题1
②一组数据的众数一定出现在这组数据中;
①众数是一组数据中出现次数最多的数据;
③一组数据可能有多个众数,也可能没有众数,众数反映了一组数据的多数水平.
2、众数的特征及意义:
例 1
例 题 精 讲
某商场进了一批苹果,每箱苹果的质量约为5千克.进入仓库前,从中随机抽出10箱称重,得到10箱苹果的质量如下:(单位:千克)
4.8,5.0, 5.1, 4.8, 4.9,4.8, 5.1, 4.9, 4.7, 4.7
请指出这10箱苹果质量的平均数、中位数和众数.
解:这10箱苹果质量的平均数为:
中位数为:4.85(千克);众数为:4.8(千克)
1.判断题(对的在括号内填“√”,错的在括号内填“×”)
(1)给定一组数据,那么这组数据的平均数一定只有一个. ( )
(2)给定一组数据,那么这组数据的中位数一定只有一个. ( )
(3)给定一组数据,那么这组数据的众数一定只有一个. ( )
(4)给定一组数据,那么这组数据的平均数一定位于最大值和最小值之间. ( )
(5)给定一组数据,那么这组数据的中位数一定等于最小值和最大值的平均数. ( )
(6)给定一组数据,如果找不到众数,那么众数一定就是 0. ( )
√
√
×
√
×
×
随 堂 练 习
2.一名警察在高速公路上随机观察了 6 辆过往车辆,它们的速度(单位: 千米/ 时)分别为: 66, 57, 71, 54, 69, 58. 那么,这 6 辆车的速度的中位数和众数分别是多少
解:这 6 辆车的速度的中位数为:62(千米/ 时)
这 6 辆车的速度的没有众数.
当 堂 检 测
1.数据 1,2, 8,5,3,9,5,4,5,4 的众数、中位数分别为( )
A.4.5、5 B.5、4.5 C.5、4 D.5、5
2.要调查多数同学们喜欢看的电视节目,应关注的是哪个数据的代表( )
A.平均数 B.中位数 C.众数
3.在演讲比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A.平均数 B.中位数 C.众数
B
C
B
4.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班 50 名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数 2 2 6 12 13 4 3
(1)填写图表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
2.44
(3)这组数据的中位数是 ,众数是 .
2.5
3
8
5.某校男子足球队的年龄分布如下面的条形图所示.请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
人数
13
14
15
16
17
18
年龄/岁
0
2
4
6
8
10
解:这些队员年龄的平均数为:(13×2+14×6+15×8+16×3+17×2+18×1)÷22 = 15,
队员年龄的众数为 15,队员年龄的中位数是 15.
意义:由平均数是 15 可说明
队员们的平均年龄为 15;
由众数是 15 可说明
大多数队员的年龄为 15 岁;
由中位数是 15 可说明有一半队员的年龄大于或等于 15 岁,有一半队员的年龄小于或等于 15 岁.
课 堂 小 结
中位数与
众数
中位数:表示一组数据的中间水平,中位数左右的数据一样多.
众数:表示一组数据的多数水平,众数可能有多个,也可能没有众数.
中位数求法三步:排序—判断(个数是奇还是偶)—确定或算出.
课 后 作 业
1.从课后习题中选取;
2.完成练习册本课时的习题.
