20.3 数据的离散程度 第1、2课时 课件 (共27张PPT) 2023-2024学年数学华师版八年级下册
文档属性
| 名称 | 20.3 数据的离散程度 第1、2课时 课件 (共27张PPT) 2023-2024学年数学华师版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 20:56:23 | ||
图片预览



文档简介
(共27张PPT)
20.3 数据的离散趋势
第1课时 方差
第2课时 用计算器求方差
学 习 目 标
1.了解方差的定义和计算公式.
2.理解方差概念的产生和形成的过程.(重点)
3.会用方差计算公式来比较两组数据的波动大小.(难点)
情 境 导 入
学校篮球联赛开始了……
教练
选 我
选 我
教练的烦恼
?
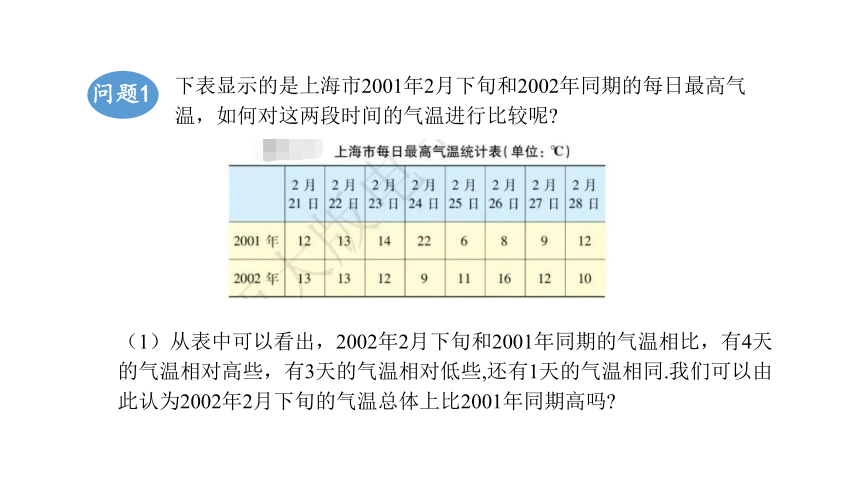
下表显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段时间的气温进行比较呢
问题1
(1)从表中可以看出,2002年2月下旬和2001年同期的气温相比,有4天的气温相对高些,有3天的气温相对低些,还有1天的气温相同.我们可以由此认为2002年2月下旬的气温总体上比2001年同期高吗
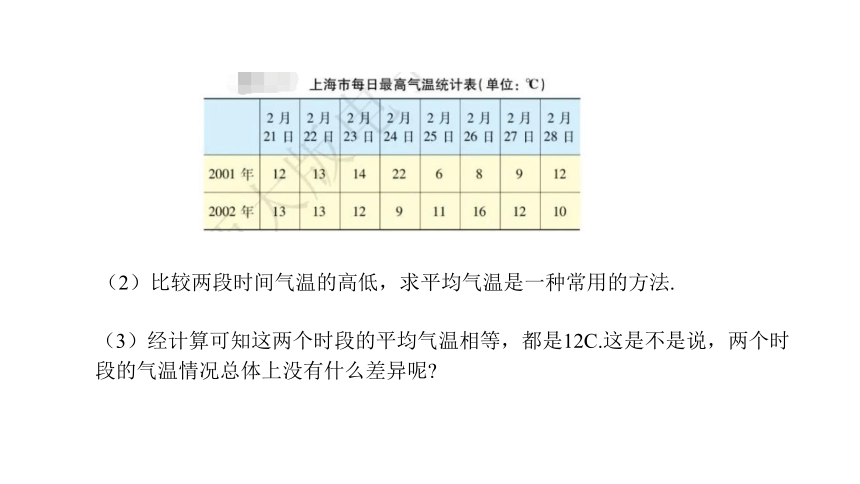
(3)经计算可知这两个时段的平均气温相等,都是12C.这是不是说,两个时段的气温情况总体上没有什么差异呢
(2)比较两段时间气温的高低,求平均气温是一种常用的方法.
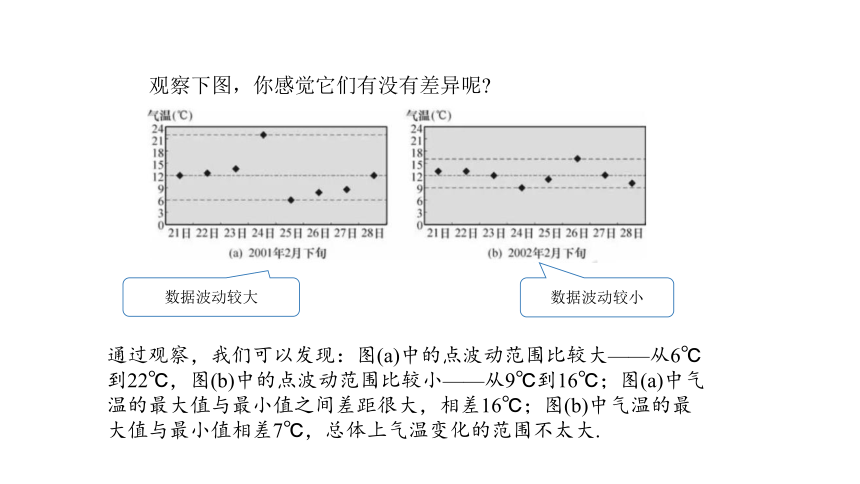
观察下图,你感觉它们有没有差异呢
数据波动较大
数据波动较小
通过观察,我们可以发现:图(a)中的点波动范围比较大——从6℃到22℃,图(b)中的点波动范围比较小——从9℃到16℃;图(a)中气温的最大值与最小值之间差距很大,相差16℃;图(b)中气温的最大值与最小值相差7℃,总体上气温变化的范围不太大.
问题2
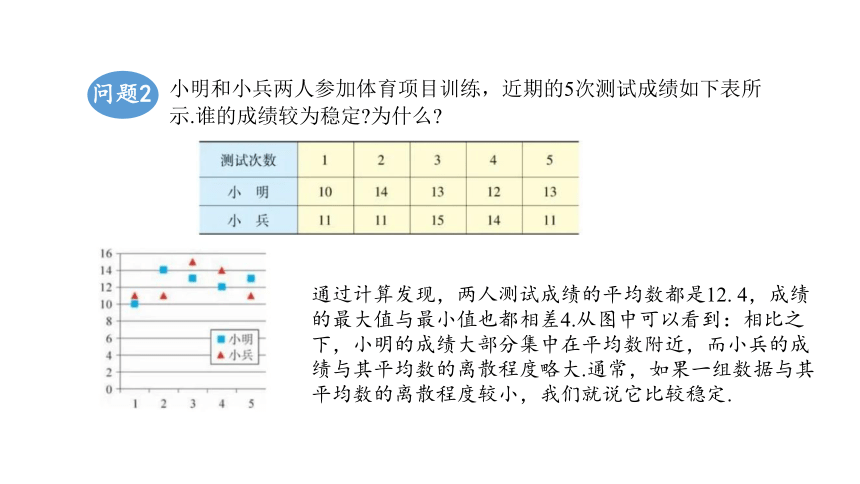
小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示.谁的成绩较为稳定 为什么
通过计算发现,两人测试成绩的平均数都是12. 4,成绩的最大值与最小值也都相差4.从图中可以看到:相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
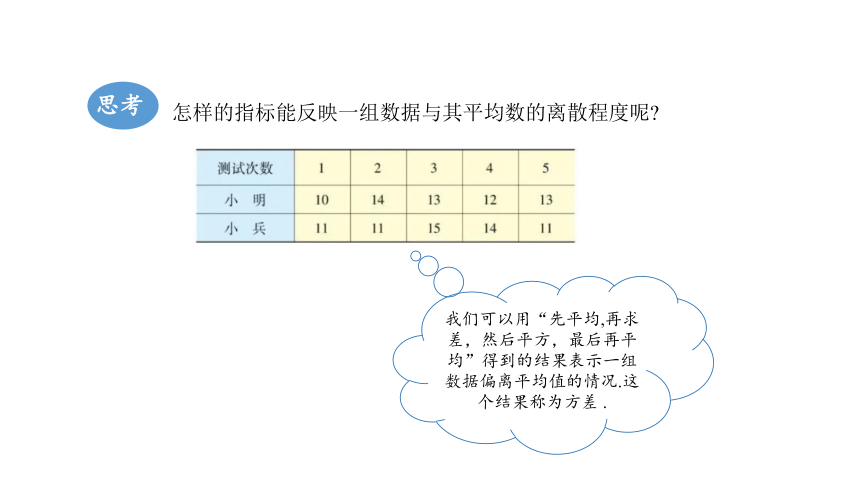
思考
怎样的指标能反映一组数据与其平均数的离散程度呢
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果称为方差 .
思考
怎样的指标能反映一组数据与其平均数的离散程度呢
∵1.84<3.04,∴小明的成绩更稳定.
知 识 讲 解
知识点1 方差
数学上,数据的离散程度还可以用方差或标准差来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
其中, 是x1,x2,……,xn的平均数,s2是方差.
一般而言,一组数据的方差越小,这组数据就越稳定.
方法拓展
任取一个基准数 a
将原数据减去 a,得到一组新数据
求新数据的方差
1
2
3
求一组较大数据的方差,有如下简便计算方法:
例 1
例 题 精 讲
人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
随 堂 练 习
1.一组数据6、4、a、3、2的平均数是5,这组数据的方差为( )
A.8 B.5 C.2 D.3
A
2.数据-2,-1,0,1,2的方差是___,标准差是___ .
3.五个数1,3,a,5,8的平均数是4,则a =_____,这五个数的方差_____.
2
3
5.6
知识点2 用计算器求方差
知 识 讲 解
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;
然后依次输入数据x1,x2,…,xn ;最后按动求方差的功能键(例如 键),计算器便会求出方差 的值.
例如:
4. SHIFT + S-Var + xσn += ;
5. 将求出的结果平方,就得到方差 .
1. MODE + 2-SD 进入SD模式;
2. SHIFT + CLR + = 清除统计存储器;
3. 输入数据,每输入一个数据后按 DT ;
例 2
例 题 精 讲
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有 .
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
①②③
随 堂 练 习
1.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 0.3
乙 84 84 34
84
90
0.5
14.4
当 堂 检 测
1.样本方差的作用是( )
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
D
① 对于数据 x1 - 3,x2 - 3,x3 - 3,…,xn - 3
平均数为 ,方差为 .
② 对于数据 x1 + 3,x2 + 3,x3 + 3,…,xn + 3
平均数为 ,方差为 .
2.若数据 x1、x2、…、xn 平均数为 ,方差为 s2,则
x
+ 3
x
- 3
x
s2
s2
结论(1): 数据 x1±b、x2±b、…、xn±b ,
平均数为 ,方差为 .
±b
x
s2
3. 小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图所示,则他这五次成绩的方差 为 .
100
4.为了考察甲、乙两种小麦的长势,分别从中抽取了10株麦苗,测得高度(单位:cm)如下:
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
哪种麦苗长势整齐?
x甲= ×(15+15+…+15)=13.9(cm),
s甲2= ×[(15-13.9)2+(15-13.9)2+…+(15-13.9)2]
=2.09,
x乙= ×(17+14+…+11)=14(cm),
s乙2= ×[(17-14)2+(14-14)2+…+(11-14)2]=2.8,
因为s甲2<s乙2,所以甲种麦苗长势整齐.
解:
-
-
5.甲、乙两名选手在相同条件下各射靶10次,每次射靶的成绩如图所示.
(1)请填写下表:
选手 平均数 方差 中位数 命中9环以上(包括9环)的次数
甲 7 1.2 1
乙 5.4
(2)请从下列三个不同的角度对这次测试结果进行分析.
①从平均数和方差相结合看,分析谁的成绩好些;
②从中位数和命中9环以上(包括9环)的次数相结合
看,分析谁的成绩好些;
③从折线图上两人射击命中的环数的走势看,分析
谁更有潜力.
解:(1)
选手 平均数 方差 中位数 命中9环以上(包括9环)的次数
甲 7 1.2 7 1
乙 7 5.4 7.5 3
(2)①从平均数上看,甲、乙射击的平均水平相同,而s甲2<s乙2,故甲射击环数的波动比乙射击环数的波动小,所以甲的成绩好些;
②由于甲、乙平均水平相同,而乙的中位数比甲大,命中9环以上(包括9环)的次数比甲多,所以乙的成绩好些;
③从折线图上看,乙的成绩基本上呈上升趋势,而甲的成绩仍在平均数附近上下波动,说明乙的竞技状态越来越好,而甲无明显提高,所以乙更有潜力.
课 堂 小 结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
课 后 作 业
1.从课后习题中选取;
2.完成练习册本课时的习题.
20.3 数据的离散趋势
第1课时 方差
第2课时 用计算器求方差
学 习 目 标
1.了解方差的定义和计算公式.
2.理解方差概念的产生和形成的过程.(重点)
3.会用方差计算公式来比较两组数据的波动大小.(难点)
情 境 导 入
学校篮球联赛开始了……
教练
选 我
选 我
教练的烦恼
?
下表显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段时间的气温进行比较呢
问题1
(1)从表中可以看出,2002年2月下旬和2001年同期的气温相比,有4天的气温相对高些,有3天的气温相对低些,还有1天的气温相同.我们可以由此认为2002年2月下旬的气温总体上比2001年同期高吗
(3)经计算可知这两个时段的平均气温相等,都是12C.这是不是说,两个时段的气温情况总体上没有什么差异呢
(2)比较两段时间气温的高低,求平均气温是一种常用的方法.
观察下图,你感觉它们有没有差异呢
数据波动较大
数据波动较小
通过观察,我们可以发现:图(a)中的点波动范围比较大——从6℃到22℃,图(b)中的点波动范围比较小——从9℃到16℃;图(a)中气温的最大值与最小值之间差距很大,相差16℃;图(b)中气温的最大值与最小值相差7℃,总体上气温变化的范围不太大.
问题2
小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示.谁的成绩较为稳定 为什么
通过计算发现,两人测试成绩的平均数都是12. 4,成绩的最大值与最小值也都相差4.从图中可以看到:相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
思考
怎样的指标能反映一组数据与其平均数的离散程度呢
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果称为方差 .
思考
怎样的指标能反映一组数据与其平均数的离散程度呢
∵1.84<3.04,∴小明的成绩更稳定.
知 识 讲 解
知识点1 方差
数学上,数据的离散程度还可以用方差或标准差来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
其中, 是x1,x2,……,xn的平均数,s2是方差.
一般而言,一组数据的方差越小,这组数据就越稳定.
方法拓展
任取一个基准数 a
将原数据减去 a,得到一组新数据
求新数据的方差
1
2
3
求一组较大数据的方差,有如下简便计算方法:
例 1
例 题 精 讲
人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
随 堂 练 习
1.一组数据6、4、a、3、2的平均数是5,这组数据的方差为( )
A.8 B.5 C.2 D.3
A
2.数据-2,-1,0,1,2的方差是___,标准差是___ .
3.五个数1,3,a,5,8的平均数是4,则a =_____,这五个数的方差_____.
2
3
5.6
知识点2 用计算器求方差
知 识 讲 解
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;
然后依次输入数据x1,x2,…,xn ;最后按动求方差的功能键(例如 键),计算器便会求出方差 的值.
例如:
4. SHIFT + S-Var + xσn += ;
5. 将求出的结果平方,就得到方差 .
1. MODE + 2-SD 进入SD模式;
2. SHIFT + CLR + = 清除统计存储器;
3. 输入数据,每输入一个数据后按 DT ;
例 2
例 题 精 讲
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有 .
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
①②③
随 堂 练 习
1.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 0.3
乙 84 84 34
84
90
0.5
14.4
当 堂 检 测
1.样本方差的作用是( )
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
D
① 对于数据 x1 - 3,x2 - 3,x3 - 3,…,xn - 3
平均数为 ,方差为 .
② 对于数据 x1 + 3,x2 + 3,x3 + 3,…,xn + 3
平均数为 ,方差为 .
2.若数据 x1、x2、…、xn 平均数为 ,方差为 s2,则
x
+ 3
x
- 3
x
s2
s2
结论(1): 数据 x1±b、x2±b、…、xn±b ,
平均数为 ,方差为 .
±b
x
s2
3. 小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图所示,则他这五次成绩的方差 为 .
100
4.为了考察甲、乙两种小麦的长势,分别从中抽取了10株麦苗,测得高度(单位:cm)如下:
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
哪种麦苗长势整齐?
x甲= ×(15+15+…+15)=13.9(cm),
s甲2= ×[(15-13.9)2+(15-13.9)2+…+(15-13.9)2]
=2.09,
x乙= ×(17+14+…+11)=14(cm),
s乙2= ×[(17-14)2+(14-14)2+…+(11-14)2]=2.8,
因为s甲2<s乙2,所以甲种麦苗长势整齐.
解:
-
-
5.甲、乙两名选手在相同条件下各射靶10次,每次射靶的成绩如图所示.
(1)请填写下表:
选手 平均数 方差 中位数 命中9环以上(包括9环)的次数
甲 7 1.2 1
乙 5.4
(2)请从下列三个不同的角度对这次测试结果进行分析.
①从平均数和方差相结合看,分析谁的成绩好些;
②从中位数和命中9环以上(包括9环)的次数相结合
看,分析谁的成绩好些;
③从折线图上两人射击命中的环数的走势看,分析
谁更有潜力.
解:(1)
选手 平均数 方差 中位数 命中9环以上(包括9环)的次数
甲 7 1.2 7 1
乙 7 5.4 7.5 3
(2)①从平均数上看,甲、乙射击的平均水平相同,而s甲2<s乙2,故甲射击环数的波动比乙射击环数的波动小,所以甲的成绩好些;
②由于甲、乙平均水平相同,而乙的中位数比甲大,命中9环以上(包括9环)的次数比甲多,所以乙的成绩好些;
③从折线图上看,乙的成绩基本上呈上升趋势,而甲的成绩仍在平均数附近上下波动,说明乙的竞技状态越来越好,而甲无明显提高,所以乙更有潜力.
课 堂 小 结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
课 后 作 业
1.从课后习题中选取;
2.完成练习册本课时的习题.
