8.4 三元一次方程组的解法 课件(共22张PPT)-七年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 8.4 三元一次方程组的解法 课件(共22张PPT)-七年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 811.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览







文档简介
第8.4 三元一次方程组的解法
人教版数学七年级下册
1.了解三元一次方程组的概念.能解简单的三元一次方程组,进一步体会“消元”思想.
2.会利用三元一次方程组解决实际问题,进一步提高分析问题、解决问题的能力.
学习目标
小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元的纸币的张数是2元纸币张数的4倍,求1元、2元、5元纸币各多少张.
问1:想一想题干中有哪些数量关系?
1元纸币张数+2元纸币张数+5元纸币张数=总张数
1元纸币金额+2元纸币金额+5元纸币金额=总金额
1元纸币张数= 2元纸币张数×4
问2:可以怎样设未知数列出方程?
情境引入
解:设1元纸币x张,2元纸币y张,5元纸币z张.
x+y+z=12
x+2y+5z=22
x=4y
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
如何求解三元一次方程组?
探究新知
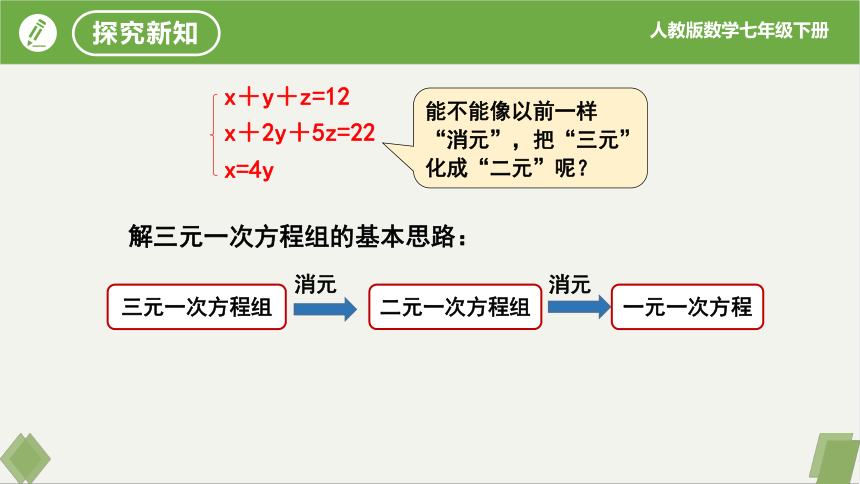
x+y+z=12
x+2y+5z=22
x=4y
解三元一次方程组的基本思路:
消元
消元
一元一次方程
二元一次方程组
三元一次方程组
能不能像以前一样“消元”,把“三元”化成“二元”呢?
探究新知
x+y+z=12 ①
x+2y+5z=22 ②
x=4y ③
解:把③带入①、②,得到关于y、z的方程组
5y+z=12 ④
6y+5z=22 ⑤
由④×5,得25y+5z=60 ⑥
由⑥-⑤,得19y=38,解得y=2
把y=2代入④,得z=2
把y=2代入③,得x=8
x=8
y=2
z=2
所以这个方程组的解为
探究新知
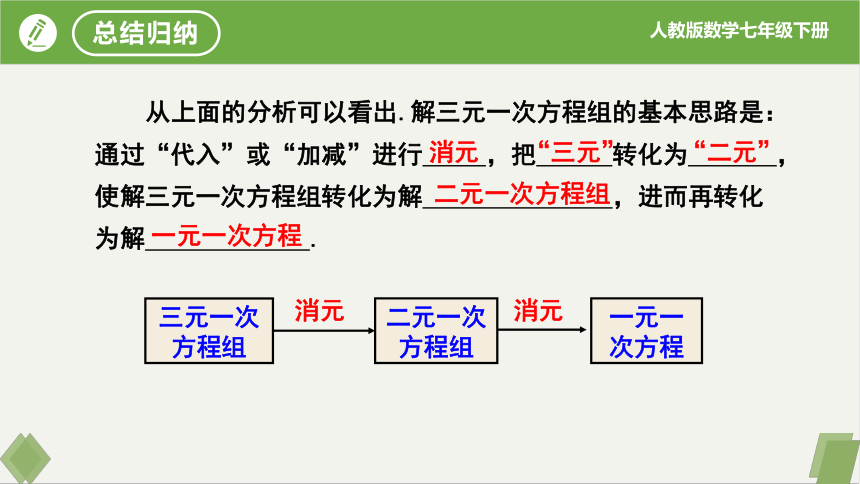
从上面的分析可以看出.解三元一次方程组的基本思路是:通过“代入”或“加减”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
“三元”
“二元”
二元一次方程组
一元一次方程
总结归纳
例1 解三元一次方程组
解:②×3+③,得11x+10z=35. ④
①与④组成方程组
解这个方程组,得
分析:方程①只含x,z,因此,可以由②③消去y, 得到一个只含x,z 的方程,与方程①组成一个二元一次方程组.
例题讲解
例1 解三元一次方程组
把x=5,z=-2代人②,得 2×5+3y-2=9,
所以?
因此,这个三元一次方程组的解为
例题讲解
例2 在等式y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60.求a,b,c的值.
分析:把a,b,c 看成三个未知数,分别把已知的x,y值代入原等式,就可以得到一个三元一次方程组.
解:根据题意,得三元一次方程组
例题讲解
②-①,得a+b=1; ④
③-①,得4a+b=10. ⑤
④与⑤组成二元一次方程组
解这个方程组,得
把 代入①,得c=-5.
因此 即a,b,c 的值分别为3,-2,-5.
例题讲解
1.变形:将三元一次方程组通过消元变为为二元一次方程组;
2.求解:解二元一次方程组;
3.回代:将求得的未知数的值代入原方程组的一个适当的方程中,得到一个一元一次方程;
4.求解:解一元一次方程,求出第三个未知数;
5.写解:用大括号将所求的的三个未知数的值联立起来,即得原方程组的解.
解三元一次方程组的基本步骤:
总结归纳
1.解方程组
解:由方程②得 x=y+1 ④
把④分别代入①③得 2y+z=22 ⑤
3y-z=18 ⑥
解由⑤⑥组成的二元一次方程组,得y=8,z=6
把y=8代入④,得x=9
所以原方程的解是
?
?
?
x=9
y=8
z=6
随堂检测
2.有甲、乙、丙三种文具,购买甲1件,乙2件比购买丙1件多花9元;购买甲2件,丙8件比购买乙1件多花18元.现在购买甲、乙、丙各一件文具,则共需花费 元.?
9
随堂检测
1.解方程组:
解:①+②+③,得2x+2y+2z=12,
所以x+y+z=6.④
④-①,得z=3.
④-②,得x=1.
④-③,得y=2.
所以原方程组的解为
巩固练习
2. 甲、乙、丙三个数的和是 35,甲数的 2 倍比乙数大 5,乙数的????????等于丙数的?????????,求这三个数.
?
解:设甲乙、丙三数分别为x、y、z,
则
解得
∴甲数是10,乙数是15,丙数是10.
巩固练习
1.某农场有300名职工耕种51公顷土 地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
已知该农场计划投入67万元,应该怎样安排这三种农作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
农作物品种
每公顷需劳动力
每公顷需设备资金
水稻
4人
1万元
棉花
8人
1万元
蔬菜
5人
2万元
拓展训练
解:设种植水稻、棉花和蔬菜的面积分别为x公顷、y公顷和z公顷.
根据题意,得????+????+????=????????,????????+????????+????????=????????????,????+????+????????=????????,解得????=????????,????=????????,????=????????.
答:种植水稻、棉花和蔬菜的面积分别为15公顷、20公顷和16公顷.
?
拓展训练
三元一次方程组
三元一次方程组的概念
三元一次方程组的解法
三元一次方程组的应用
课堂小结
1.三元一次方程组?????????=????,?????????=????,????+????=????的解是( )
A.????=????,????=????,????=???? B.????=????,????=????,????=???? C.????=????,????=????,????=???? D.????=????,????=????,????=????
?
D
课后作业
2.解下列三元一次方程组:
解:③-①,得2z+2y=56,即y+z=28 ④,
②+④,得2y=31,所以y=15.5.
把y=15.5代入①,得x=22.
把y=15.5代入②,得z=12.5.
所以原方程组的解为
课后作业
谢谢聆听
人教版数学七年级下册
1.了解三元一次方程组的概念.能解简单的三元一次方程组,进一步体会“消元”思想.
2.会利用三元一次方程组解决实际问题,进一步提高分析问题、解决问题的能力.
学习目标
小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元的纸币的张数是2元纸币张数的4倍,求1元、2元、5元纸币各多少张.
问1:想一想题干中有哪些数量关系?
1元纸币张数+2元纸币张数+5元纸币张数=总张数
1元纸币金额+2元纸币金额+5元纸币金额=总金额
1元纸币张数= 2元纸币张数×4
问2:可以怎样设未知数列出方程?
情境引入
解:设1元纸币x张,2元纸币y张,5元纸币z张.
x+y+z=12
x+2y+5z=22
x=4y
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
如何求解三元一次方程组?
探究新知
x+y+z=12
x+2y+5z=22
x=4y
解三元一次方程组的基本思路:
消元
消元
一元一次方程
二元一次方程组
三元一次方程组
能不能像以前一样“消元”,把“三元”化成“二元”呢?
探究新知
x+y+z=12 ①
x+2y+5z=22 ②
x=4y ③
解:把③带入①、②,得到关于y、z的方程组
5y+z=12 ④
6y+5z=22 ⑤
由④×5,得25y+5z=60 ⑥
由⑥-⑤,得19y=38,解得y=2
把y=2代入④,得z=2
把y=2代入③,得x=8
x=8
y=2
z=2
所以这个方程组的解为
探究新知
从上面的分析可以看出.解三元一次方程组的基本思路是:通过“代入”或“加减”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
“三元”
“二元”
二元一次方程组
一元一次方程
总结归纳
例1 解三元一次方程组
解:②×3+③,得11x+10z=35. ④
①与④组成方程组
解这个方程组,得
分析:方程①只含x,z,因此,可以由②③消去y, 得到一个只含x,z 的方程,与方程①组成一个二元一次方程组.
例题讲解
例1 解三元一次方程组
把x=5,z=-2代人②,得 2×5+3y-2=9,
所以?
因此,这个三元一次方程组的解为
例题讲解
例2 在等式y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60.求a,b,c的值.
分析:把a,b,c 看成三个未知数,分别把已知的x,y值代入原等式,就可以得到一个三元一次方程组.
解:根据题意,得三元一次方程组
例题讲解
②-①,得a+b=1; ④
③-①,得4a+b=10. ⑤
④与⑤组成二元一次方程组
解这个方程组,得
把 代入①,得c=-5.
因此 即a,b,c 的值分别为3,-2,-5.
例题讲解
1.变形:将三元一次方程组通过消元变为为二元一次方程组;
2.求解:解二元一次方程组;
3.回代:将求得的未知数的值代入原方程组的一个适当的方程中,得到一个一元一次方程;
4.求解:解一元一次方程,求出第三个未知数;
5.写解:用大括号将所求的的三个未知数的值联立起来,即得原方程组的解.
解三元一次方程组的基本步骤:
总结归纳
1.解方程组
解:由方程②得 x=y+1 ④
把④分别代入①③得 2y+z=22 ⑤
3y-z=18 ⑥
解由⑤⑥组成的二元一次方程组,得y=8,z=6
把y=8代入④,得x=9
所以原方程的解是
?
?
?
x=9
y=8
z=6
随堂检测
2.有甲、乙、丙三种文具,购买甲1件,乙2件比购买丙1件多花9元;购买甲2件,丙8件比购买乙1件多花18元.现在购买甲、乙、丙各一件文具,则共需花费 元.?
9
随堂检测
1.解方程组:
解:①+②+③,得2x+2y+2z=12,
所以x+y+z=6.④
④-①,得z=3.
④-②,得x=1.
④-③,得y=2.
所以原方程组的解为
巩固练习
2. 甲、乙、丙三个数的和是 35,甲数的 2 倍比乙数大 5,乙数的????????等于丙数的?????????,求这三个数.
?
解:设甲乙、丙三数分别为x、y、z,
则
解得
∴甲数是10,乙数是15,丙数是10.
巩固练习
1.某农场有300名职工耕种51公顷土 地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
已知该农场计划投入67万元,应该怎样安排这三种农作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
农作物品种
每公顷需劳动力
每公顷需设备资金
水稻
4人
1万元
棉花
8人
1万元
蔬菜
5人
2万元
拓展训练
解:设种植水稻、棉花和蔬菜的面积分别为x公顷、y公顷和z公顷.
根据题意,得????+????+????=????????,????????+????????+????????=????????????,????+????+????????=????????,解得????=????????,????=????????,????=????????.
答:种植水稻、棉花和蔬菜的面积分别为15公顷、20公顷和16公顷.
?
拓展训练
三元一次方程组
三元一次方程组的概念
三元一次方程组的解法
三元一次方程组的应用
课堂小结
1.三元一次方程组?????????=????,?????????=????,????+????=????的解是( )
A.????=????,????=????,????=???? B.????=????,????=????,????=???? C.????=????,????=????,????=???? D.????=????,????=????,????=????
?
D
课后作业
2.解下列三元一次方程组:
解:③-①,得2z+2y=56,即y+z=28 ④,
②+④,得2y=31,所以y=15.5.
把y=15.5代入①,得x=22.
把y=15.5代入②,得z=12.5.
所以原方程组的解为
课后作业
谢谢聆听
