9.2 多边形的内角和与外角和 课件(共36张PPT)-七年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 9.2 多边形的内角和与外角和 课件(共36张PPT)-七年级数学下册同步精品课堂(华东师大版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
(共36张PPT)
9.2 多边形的内角和与外角和
数学(华东师大版)
七年级 下册
第9章 多边形
学习目标
1、掌握多边形的相关概念.
2、会用分割法探索多边形的内角和计算公式;
3、运用多边形的内角和计算公式解决问题;
导入新课
生活中的平面图形
三角形
长方形
四边形
六边形
八边形
讲授新课
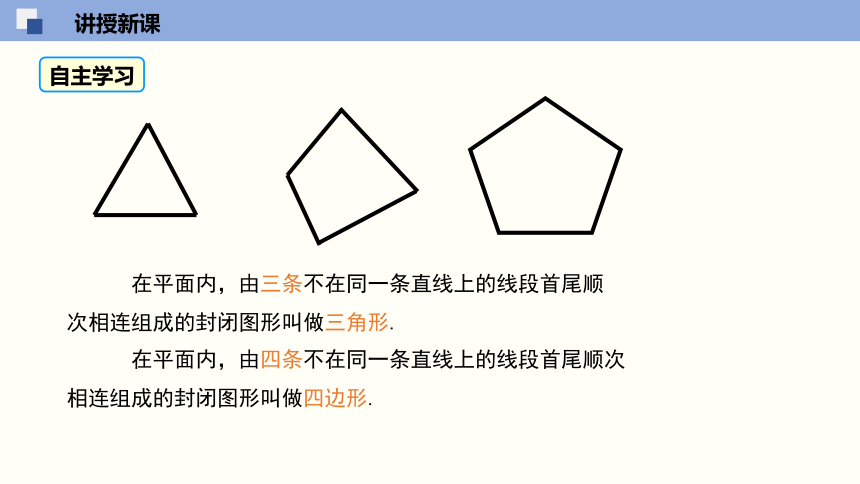
知识点一 多边形的相关概念
多边形的概念
回顾:
什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
思考:
你能根据三角形的定义归纳出什么叫做多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
讲授新课
自主学面内,由三条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做三角形.
在平面内,由四条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做四边形.
讲授新课
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
在平面内,由五条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做五边形.
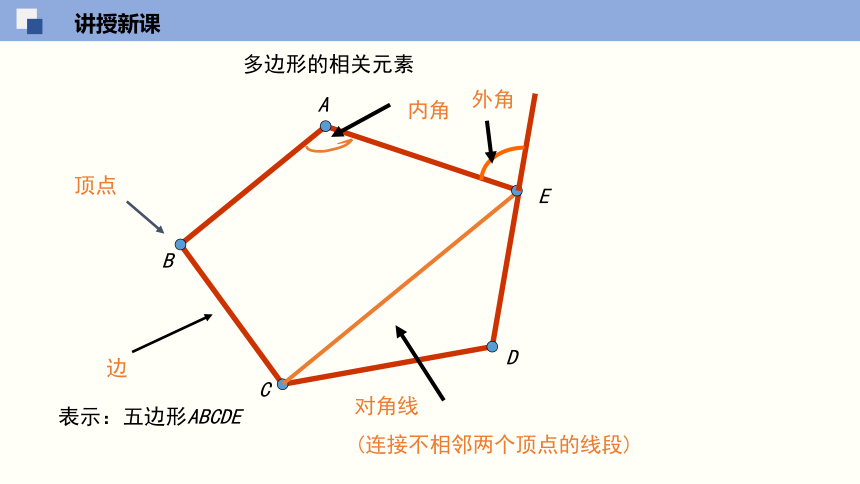
组成多边形的各条线段叫作多边形的边.
相邻两条边的公共端点叫作多边形的顶点.
连接不相邻的两个顶点的线段叫作多边形的对角线.
相邻两边组成的角叫作多边形的内角,简称多边形的角.
讲授新课
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
多边形的相关元素
外角
表示:五边形ABCDE
A
C
B
D
E
讲授新课
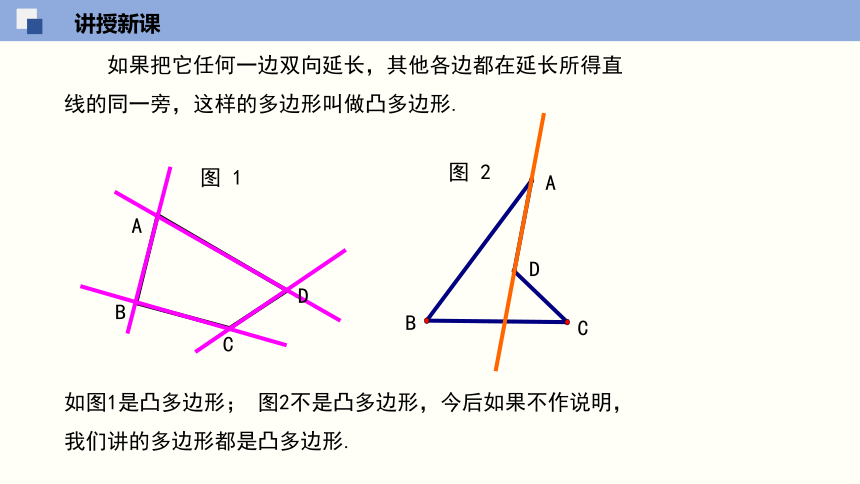
如图1是凸多边形; 图2不是凸多边形,今后如果不作说明,我们讲的多边形都是凸多边形.
图 2
如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
图 1
A
C
B
D
A
C
B
D
讲授新课
在平面内,边相等、角也都相等的多边形叫正多边形.
问题 观察下面多边形,它们的边、角有什么特点?
特点:
各边相等,各内角都相等的多边形.
讲授新课
典例精析
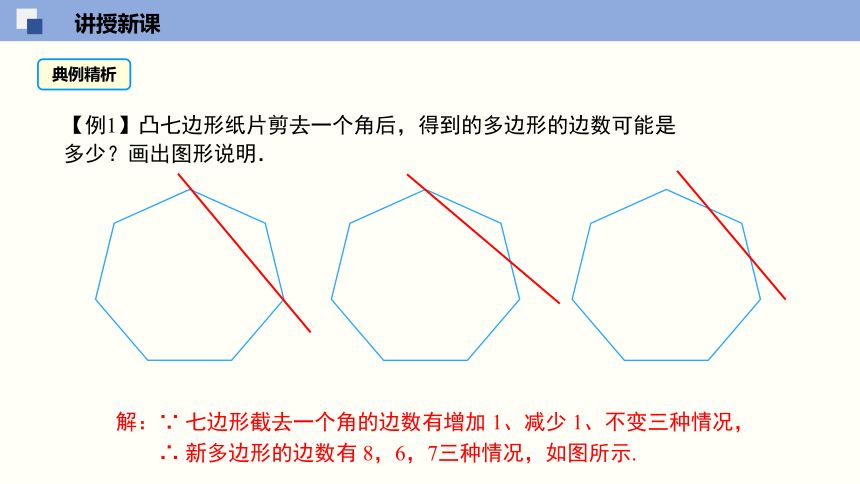
【例1】凸七边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵ 七边形截去一个角的边数有增加 1、减少 1、不变三种情况,
∴ 新多边形的边数有 8,6,7三种情况,如图所示.
讲授新课
练一练
2、已知多边形的某一个顶点可以做出2021条对角线,求这个多边形的边数.
解:设多边形有n 条边,则从一个顶点出发可以引出(n-3)对角线,
根据题意,得n-3=2021,解得n=2024.
1、九边形从一个顶点可以引出( )条对角线,分割出( )个
三角形,共有对角线( )条.
解:从一个顶点可以引出对角线条数为9-3=6.
分割出的三角形个数为9-2=7.
共有对角线条数为9×(9-3)/2=27 .
6
7
27
讲授新课
知识点二 多边形的内角和
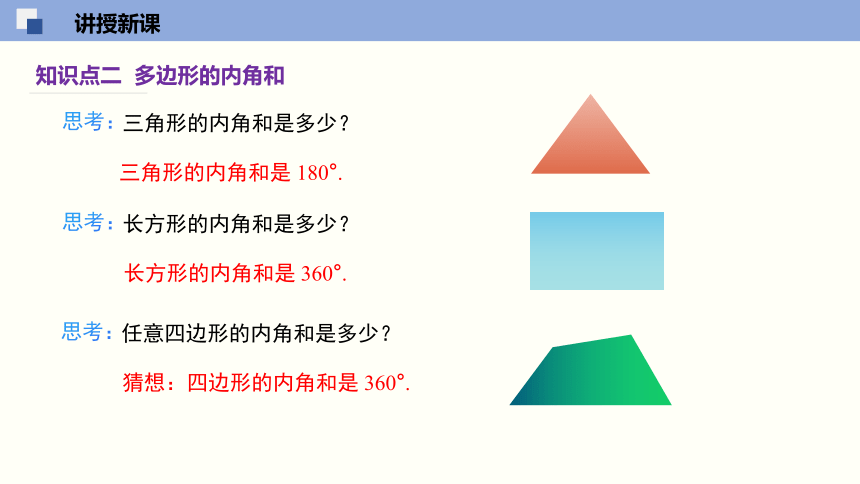
思考:
三角形的内角和是多少?
三角形的内角和是 180°.
思考:
长方形的内角和是多少?
长方形的内角和是 360°.
思考:
任意四边形的内角和是多少?
猜想:四边形的内角和是 360°.
讲授新课
思考:
如何证明四边形的内角和为360°?
法一
证明:如图,连接 AC.
则四边形被分为两个三角形,
所以四边形 ABCD 的内角和为
180°×2 = 360°.
A
B
C
D
提示:
四边形能否分成两个三角形?
讲授新课
思考:
你还能想出什么方法证明四边形的内角和为360°?
法二
提示:
四边形能否分成两三个三角形?
如图,在 BC 边上任取一点 E,
连接 AE,DE,
则该四边形被分成三个三角形,
所以四边形 ABCD 的内角和为
180°×3 - (∠AEB+∠AED+∠CED)
= 180°×3 - 180°
= 360°.
A
B
C
D
E
讲授新课
思考:
你还能想出什么方法证明四边形的内角和为360°?
法三
提示:
四边形能否分成两四个三角形?
如图,在四边形 ABCD 内部任取一点 E,
连接 AE,BE,CE,DE,
把四边形分成四个三角形:
△ABE,△ADE,△CDE,△CBE.
所以四边形 ABCD 的内角和为
180°×4 - (∠AEB + ∠AED
+∠CED +∠CEB)= 720° - 360° = 360°.
A
B
C
D
E
讲授新课
试一试 在下列各个多边形中,任取一个顶点,通过该顶点画出所有对角线,完成下表.
五边形
六边形
七边形
八边形
讲授新课
五边形 5 3
(5-2) × 180°
六边形 6
七边形 7
图形 边数
可分成三角形的个数
多边形的内角和
五边形
六边形
八边形 8
… … … …
n边形 n
4
(6-2) × 180°
(7-2) × 180°
5
(8-2) × 180°
6
n-2
(n-2)×180°
五边形
六边形
七边形
八边形
规律总结
讲授新课
n边形的内角和等于(n-2)· 180°.
归纳总结
讲授新课
典例精析
【例2】求下列图形中 的值.
∟
(1)
(2)
解:
(1)根据四边形的内角和为360°可得,
140+90+2x=360
解得x=65
(2)根据四边形的内角和为360°可得,
120+80+75+x=360
解得x=85
讲授新课
练一练
1、如图,在四边形 ABCD 中,∠A 与∠C 互补,BE 平分∠ABC,DF 平分∠ADC,若 BE∥DF,求证:△DCF 为直角三角形.
证明:∵ 在四边形 ABCD 中,∠A 与∠C 互补,
∴∠ABC +∠ADC = 180°.
∵ BE 平分∠ABC,DF 平分∠ADC,
∴∠CDF +∠EBF = 90°.
∵ BE∥DF,∴∠EBF = ∠CFD,
∴∠CDF +∠CFD = 90°.
∴△DCF 为直角三角形.
讲授新课
2、已知在一个十边形中,九个内角的和的度数是1290°,求这个十边形的另一个内角的度数.
解:这个十边形的内角和为
(10-2)×180° =1440 °
则十边形的另一个内角的度数为
1440 °- 1290° =150 °
讲授新课
3、一个同学在进行多边形的内角和计算时,求得内角和为 1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
解:设此多边形的内角和为 x,
则有 1125°<x<1125°+180°,
即 180°×6+45°<x<180°×7+45°.
∵ x 为多边形的内角和,所以它是 180° 的倍数,
∴ x=180°×7=1260°.
∴ 7+2=9,1260°-1125°=135°.
因此,漏加的这个内角是 135°,这个多边形是九边形.
讲授新课
知识点三 多边形的外角和
问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
讲授新课
E
B
C
D
1
2
3
4
5
A
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
讲授新课
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
E
B
C
D
1
2
3
4
n
A
任意多边形的外角和等于360°.
归纳总结
讲授新课
典例精析
【例3】已知一个多边形,它的内角和等于外角和的5倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360°,
∴ (n-2) 180°=5× 360 .
解得 n=12.
∴这个多边形的边数为12.
讲授新课
练一练
1、已知某正多边形的每个外角都是 72°,则这个多边形
是正____边形.
分析:因为正多边形的每一个外角都是72°,
则这个正多边形的每一个内角都是180°-72°=108°,
根据多边形内角和公式可得
解得n =5
因此这个多边形是正五边形.
( n - 2 )·180°=n ·108°
讲授新课
2、已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x °,外角为2x°,根据题意得
7x+2x=180,
解得x=20.
即每个内角是140 °,每个外角是40 °.
360° ÷40 °=9.
答:这个多边形是九边形.
当堂检测
1.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
A
2.过一个多边形的一个顶点的所有对角线把多边形分成5个三角形,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
C
3.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
6
当堂检测
4. 一个多边形从一个顶点可引对角线 3 条,则这个多边形的内角和等于 ( )
A. 360° B. 540° C. 720° D. 900°
C
当堂检测
5.求下列图形中的x的值.
∟
D
C
A
B
E
AB∥CD
解:
x=[(5-2)×180-90-150-120]÷3=60
解:
x=(5-2)×180-135-150-180=75
当堂检测
6.过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为 21,求这个多边形的边数.
解:设这个多边形为 n 边形,则有 (n - 3) 条对角线,所分得的三角形个数为 (n - 2),
∴ n - 3 + n - 2 = 21,
解得 n = 13.
答:该多边形的边数为 13.
当堂检测
7.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,在四边形 ABCD 中,
∠A +∠C = 180°.
∠A +∠B +∠C +∠D = 360°,
因为
∠B +∠D = 360° - (∠A +∠C )
= 360° - 180° = 180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角也互补.
当堂检测
8.如图,在五边形 ABCDE 中,∠C = 100°,∠D = 75°,∠E = 135°,AP 平分∠EAB,BP 平分∠ABC,求∠P 的度数.
解:∵∠EAB +∠ABC +∠C +∠D +∠E = 540°,
∠C = 100°,∠D = 75°,∠E = 135°,
∴∠EAB +∠ABC = 540° - 100° - 75° - 135° = 230°.
∵AP 平分∠EAB,
∴∠PAB = ∠EAB.
同理可得∠ABP = ∠ABC.
∵∠P +∠PAB +∠PBA = 180°,
∴∠P = 180°-∠PAB-∠PBA
= 180° (∠EAB+∠ABC) = 180° ×230° = 65°.
课堂小结
多边形的内角和与外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
多边形的相关概念
多边形的外角和等于360°
特别注意:与边数无关。
外角和计算公式
谢 谢~
9.2 多边形的内角和与外角和
数学(华东师大版)
七年级 下册
第9章 多边形
学习目标
1、掌握多边形的相关概念.
2、会用分割法探索多边形的内角和计算公式;
3、运用多边形的内角和计算公式解决问题;
导入新课
生活中的平面图形
三角形
长方形
四边形
六边形
八边形
讲授新课
知识点一 多边形的相关概念
多边形的概念
回顾:
什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
思考:
你能根据三角形的定义归纳出什么叫做多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
讲授新课
自主学面内,由三条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做三角形.
在平面内,由四条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做四边形.
讲授新课
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
在平面内,由五条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做五边形.
组成多边形的各条线段叫作多边形的边.
相邻两条边的公共端点叫作多边形的顶点.
连接不相邻的两个顶点的线段叫作多边形的对角线.
相邻两边组成的角叫作多边形的内角,简称多边形的角.
讲授新课
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
多边形的相关元素
外角
表示:五边形ABCDE
A
C
B
D
E
讲授新课
如图1是凸多边形; 图2不是凸多边形,今后如果不作说明,我们讲的多边形都是凸多边形.
图 2
如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
图 1
A
C
B
D
A
C
B
D
讲授新课
在平面内,边相等、角也都相等的多边形叫正多边形.
问题 观察下面多边形,它们的边、角有什么特点?
特点:
各边相等,各内角都相等的多边形.
讲授新课
典例精析
【例1】凸七边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵ 七边形截去一个角的边数有增加 1、减少 1、不变三种情况,
∴ 新多边形的边数有 8,6,7三种情况,如图所示.
讲授新课
练一练
2、已知多边形的某一个顶点可以做出2021条对角线,求这个多边形的边数.
解:设多边形有n 条边,则从一个顶点出发可以引出(n-3)对角线,
根据题意,得n-3=2021,解得n=2024.
1、九边形从一个顶点可以引出( )条对角线,分割出( )个
三角形,共有对角线( )条.
解:从一个顶点可以引出对角线条数为9-3=6.
分割出的三角形个数为9-2=7.
共有对角线条数为9×(9-3)/2=27 .
6
7
27
讲授新课
知识点二 多边形的内角和
思考:
三角形的内角和是多少?
三角形的内角和是 180°.
思考:
长方形的内角和是多少?
长方形的内角和是 360°.
思考:
任意四边形的内角和是多少?
猜想:四边形的内角和是 360°.
讲授新课
思考:
如何证明四边形的内角和为360°?
法一
证明:如图,连接 AC.
则四边形被分为两个三角形,
所以四边形 ABCD 的内角和为
180°×2 = 360°.
A
B
C
D
提示:
四边形能否分成两个三角形?
讲授新课
思考:
你还能想出什么方法证明四边形的内角和为360°?
法二
提示:
四边形能否分成两三个三角形?
如图,在 BC 边上任取一点 E,
连接 AE,DE,
则该四边形被分成三个三角形,
所以四边形 ABCD 的内角和为
180°×3 - (∠AEB+∠AED+∠CED)
= 180°×3 - 180°
= 360°.
A
B
C
D
E
讲授新课
思考:
你还能想出什么方法证明四边形的内角和为360°?
法三
提示:
四边形能否分成两四个三角形?
如图,在四边形 ABCD 内部任取一点 E,
连接 AE,BE,CE,DE,
把四边形分成四个三角形:
△ABE,△ADE,△CDE,△CBE.
所以四边形 ABCD 的内角和为
180°×4 - (∠AEB + ∠AED
+∠CED +∠CEB)= 720° - 360° = 360°.
A
B
C
D
E
讲授新课
试一试 在下列各个多边形中,任取一个顶点,通过该顶点画出所有对角线,完成下表.
五边形
六边形
七边形
八边形
讲授新课
五边形 5 3
(5-2) × 180°
六边形 6
七边形 7
图形 边数
可分成三角形的个数
多边形的内角和
五边形
六边形
八边形 8
… … … …
n边形 n
4
(6-2) × 180°
(7-2) × 180°
5
(8-2) × 180°
6
n-2
(n-2)×180°
五边形
六边形
七边形
八边形
规律总结
讲授新课
n边形的内角和等于(n-2)· 180°.
归纳总结
讲授新课
典例精析
【例2】求下列图形中 的值.
∟
(1)
(2)
解:
(1)根据四边形的内角和为360°可得,
140+90+2x=360
解得x=65
(2)根据四边形的内角和为360°可得,
120+80+75+x=360
解得x=85
讲授新课
练一练
1、如图,在四边形 ABCD 中,∠A 与∠C 互补,BE 平分∠ABC,DF 平分∠ADC,若 BE∥DF,求证:△DCF 为直角三角形.
证明:∵ 在四边形 ABCD 中,∠A 与∠C 互补,
∴∠ABC +∠ADC = 180°.
∵ BE 平分∠ABC,DF 平分∠ADC,
∴∠CDF +∠EBF = 90°.
∵ BE∥DF,∴∠EBF = ∠CFD,
∴∠CDF +∠CFD = 90°.
∴△DCF 为直角三角形.
讲授新课
2、已知在一个十边形中,九个内角的和的度数是1290°,求这个十边形的另一个内角的度数.
解:这个十边形的内角和为
(10-2)×180° =1440 °
则十边形的另一个内角的度数为
1440 °- 1290° =150 °
讲授新课
3、一个同学在进行多边形的内角和计算时,求得内角和为 1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
解:设此多边形的内角和为 x,
则有 1125°<x<1125°+180°,
即 180°×6+45°<x<180°×7+45°.
∵ x 为多边形的内角和,所以它是 180° 的倍数,
∴ x=180°×7=1260°.
∴ 7+2=9,1260°-1125°=135°.
因此,漏加的这个内角是 135°,这个多边形是九边形.
讲授新课
知识点三 多边形的外角和
问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
讲授新课
E
B
C
D
1
2
3
4
5
A
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
讲授新课
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
E
B
C
D
1
2
3
4
n
A
任意多边形的外角和等于360°.
归纳总结
讲授新课
典例精析
【例3】已知一个多边形,它的内角和等于外角和的5倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360°,
∴ (n-2) 180°=5× 360 .
解得 n=12.
∴这个多边形的边数为12.
讲授新课
练一练
1、已知某正多边形的每个外角都是 72°,则这个多边形
是正____边形.
分析:因为正多边形的每一个外角都是72°,
则这个正多边形的每一个内角都是180°-72°=108°,
根据多边形内角和公式可得
解得n =5
因此这个多边形是正五边形.
( n - 2 )·180°=n ·108°
讲授新课
2、已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x °,外角为2x°,根据题意得
7x+2x=180,
解得x=20.
即每个内角是140 °,每个外角是40 °.
360° ÷40 °=9.
答:这个多边形是九边形.
当堂检测
1.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
A
2.过一个多边形的一个顶点的所有对角线把多边形分成5个三角形,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
C
3.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
6
当堂检测
4. 一个多边形从一个顶点可引对角线 3 条,则这个多边形的内角和等于 ( )
A. 360° B. 540° C. 720° D. 900°
C
当堂检测
5.求下列图形中的x的值.
∟
D
C
A
B
E
AB∥CD
解:
x=[(5-2)×180-90-150-120]÷3=60
解:
x=(5-2)×180-135-150-180=75
当堂检测
6.过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为 21,求这个多边形的边数.
解:设这个多边形为 n 边形,则有 (n - 3) 条对角线,所分得的三角形个数为 (n - 2),
∴ n - 3 + n - 2 = 21,
解得 n = 13.
答:该多边形的边数为 13.
当堂检测
7.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,在四边形 ABCD 中,
∠A +∠C = 180°.
∠A +∠B +∠C +∠D = 360°,
因为
∠B +∠D = 360° - (∠A +∠C )
= 360° - 180° = 180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角也互补.
当堂检测
8.如图,在五边形 ABCDE 中,∠C = 100°,∠D = 75°,∠E = 135°,AP 平分∠EAB,BP 平分∠ABC,求∠P 的度数.
解:∵∠EAB +∠ABC +∠C +∠D +∠E = 540°,
∠C = 100°,∠D = 75°,∠E = 135°,
∴∠EAB +∠ABC = 540° - 100° - 75° - 135° = 230°.
∵AP 平分∠EAB,
∴∠PAB = ∠EAB.
同理可得∠ABP = ∠ABC.
∵∠P +∠PAB +∠PBA = 180°,
∴∠P = 180°-∠PAB-∠PBA
= 180° (∠EAB+∠ABC) = 180° ×230° = 65°.
课堂小结
多边形的内角和与外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
多边形的相关概念
多边形的外角和等于360°
特别注意:与边数无关。
外角和计算公式
谢 谢~
