2.2.1数轴课件 (14张PPT) 2023-2024学年七年级上学期数学青岛版
文档属性
| 名称 | 2.2.1数轴课件 (14张PPT) 2023-2024学年七年级上学期数学青岛版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 849.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 08:11:30 | ||
图片预览





文档简介
(共14张PPT)
2.2.1 数轴
学习目标:
1、理解数轴的意义,弄清数轴的三要素,能正确的画出数轴。
2、会由数轴的已知点,说出它所表示的数;能将有理数用数轴上的点表示出来。
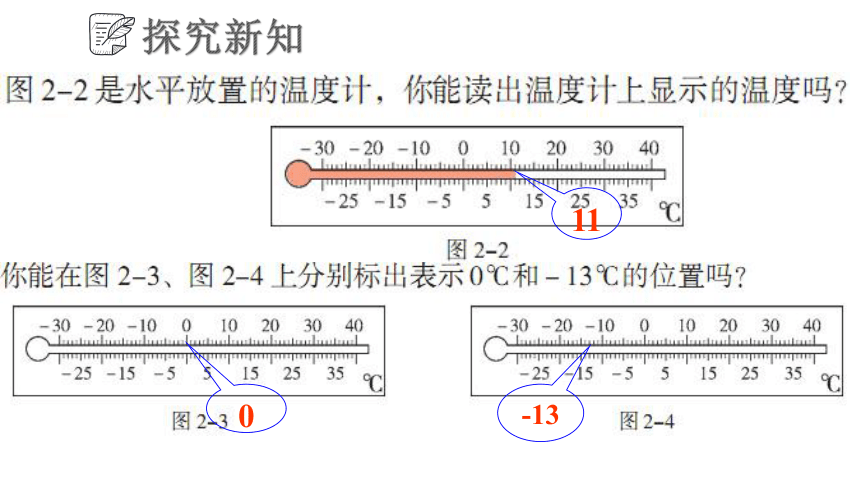
探究新知
11
0
-13
西
东
探究新知
汽
车
站
柳
树
杨
树
槐
树
电
线
杆
0
-3m
-4.8m
7.5m
3m
问题2、在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情景。
由实验探究中有刻度的温度计和带有距离数的笔直的马路,由此联想,我们能否可以用一条直线上的一些点表示有理数?
探究新知
在数学中,通常用一条直线上的点表示数,这条直线叫做数轴,它需满足以下要求:
1
0
1、画一条直线,在直线上取一点0作为原点;
2、规定直线上向右的方向为正方向;
3、根据需要选取适当长度作为单位长度,就得到了数轴。
数轴
这时我们把直线向右的方向(标上箭头)成为正方向,像这样规定了原点、单位长度和正方向的直线叫做数轴。如下图所示:
-3 -2 -1 0 1 2 3
数轴三要素:原点、正方向和单位长度。
由此可知:任何有理数都可以用数轴上唯一的一个点来表示。
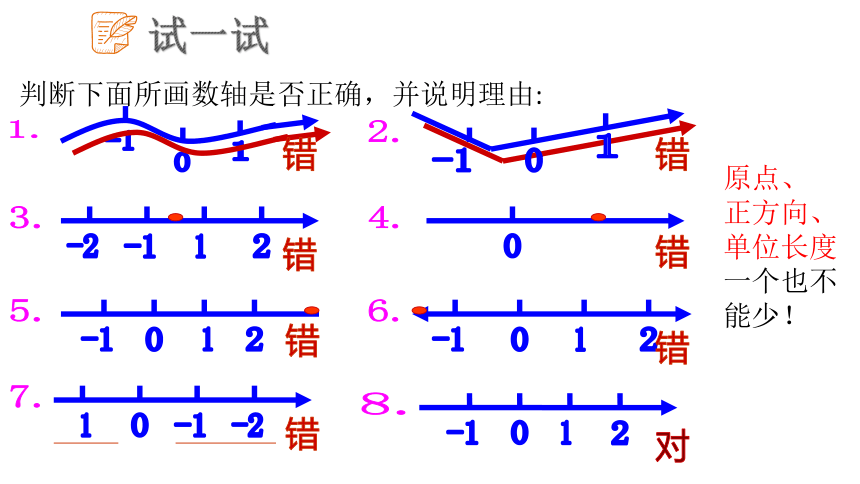
试一试
判断下面所画数轴是否正确,并说明理由:
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、
正方向、单位长度一个也不能少!
典型例题
例1 、 画出数轴,并在数轴上的点表示下列各数:
2, -1.5, 0, 3.5, -4.
0
1
2
3
4
-1
-2
-3
-4
解:
2
-1.5
0
3.5
-4
例2、 指出下图中数轴上的点A,B,C,D,E分别表示的有理数:
-4 -3 -2 -1 0 1 2 3 4 5
A B C D E
A:-4 B:-1.5 C:0 D:1.5 E :5
解:
试一试
1、在数轴上,
(1)原点右边距原点3个单位长度的点表示哪个数?
(2)原点左边距原点3.5个单位长度的点表示哪个数?
(3)原点右边距原点个单位长度的点表示哪个数?
(4)原点表示什么数?
3
-3.5
0
即学即练
2、数轴上表示-2的点在原点的( )侧,距原点的距离是( ),表示-6的点在原点的( )侧,距原点的距离是( )。
左
2个单位长
左
6个单位长
3、(判断)数轴上的两个点可以表示同一个有理数( )
错
即学即练
4、在数轴上距离原点2.5个单位长度的点所表示的数是 .
±2.5
5、如图,点A表示的数是4,那么点B表示的数是 .
-6
6、如图,数轴上点A表示的数为+3,把点A先向右平移5个单位,再向左平移10个单位到点B,则点B表示的数为 .
-2
即学即练
7、下列命题正确的是( )
A:数轴上的点都表示整数。
B:数轴上表示5与-5的点分别在原点的两侧,并且到原点的距 离都等于5个单位长度。
C:数轴只有原点与正方向两个要素。
D:数轴上的点只能表示正数和零。
B
课堂小结
1、数轴的三要素:
原点、单位长度和正方向.
2、任意一个有理数都可以用数轴上的点表示,但数轴上的点不一定都能用有理数表示!
课后作业
作业:
P35 习题 2、1
P33 练习
2.2.1 数轴
学习目标:
1、理解数轴的意义,弄清数轴的三要素,能正确的画出数轴。
2、会由数轴的已知点,说出它所表示的数;能将有理数用数轴上的点表示出来。
探究新知
11
0
-13
西
东
探究新知
汽
车
站
柳
树
杨
树
槐
树
电
线
杆
0
-3m
-4.8m
7.5m
3m
问题2、在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情景。
由实验探究中有刻度的温度计和带有距离数的笔直的马路,由此联想,我们能否可以用一条直线上的一些点表示有理数?
探究新知
在数学中,通常用一条直线上的点表示数,这条直线叫做数轴,它需满足以下要求:
1
0
1、画一条直线,在直线上取一点0作为原点;
2、规定直线上向右的方向为正方向;
3、根据需要选取适当长度作为单位长度,就得到了数轴。
数轴
这时我们把直线向右的方向(标上箭头)成为正方向,像这样规定了原点、单位长度和正方向的直线叫做数轴。如下图所示:
-3 -2 -1 0 1 2 3
数轴三要素:原点、正方向和单位长度。
由此可知:任何有理数都可以用数轴上唯一的一个点来表示。
试一试
判断下面所画数轴是否正确,并说明理由:
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、
正方向、单位长度一个也不能少!
典型例题
例1 、 画出数轴,并在数轴上的点表示下列各数:
2, -1.5, 0, 3.5, -4.
0
1
2
3
4
-1
-2
-3
-4
解:
2
-1.5
0
3.5
-4
例2、 指出下图中数轴上的点A,B,C,D,E分别表示的有理数:
-4 -3 -2 -1 0 1 2 3 4 5
A B C D E
A:-4 B:-1.5 C:0 D:1.5 E :5
解:
试一试
1、在数轴上,
(1)原点右边距原点3个单位长度的点表示哪个数?
(2)原点左边距原点3.5个单位长度的点表示哪个数?
(3)原点右边距原点个单位长度的点表示哪个数?
(4)原点表示什么数?
3
-3.5
0
即学即练
2、数轴上表示-2的点在原点的( )侧,距原点的距离是( ),表示-6的点在原点的( )侧,距原点的距离是( )。
左
2个单位长
左
6个单位长
3、(判断)数轴上的两个点可以表示同一个有理数( )
错
即学即练
4、在数轴上距离原点2.5个单位长度的点所表示的数是 .
±2.5
5、如图,点A表示的数是4,那么点B表示的数是 .
-6
6、如图,数轴上点A表示的数为+3,把点A先向右平移5个单位,再向左平移10个单位到点B,则点B表示的数为 .
-2
即学即练
7、下列命题正确的是( )
A:数轴上的点都表示整数。
B:数轴上表示5与-5的点分别在原点的两侧,并且到原点的距 离都等于5个单位长度。
C:数轴只有原点与正方向两个要素。
D:数轴上的点只能表示正数和零。
B
课堂小结
1、数轴的三要素:
原点、单位长度和正方向.
2、任意一个有理数都可以用数轴上的点表示,但数轴上的点不一定都能用有理数表示!
课后作业
作业:
P35 习题 2、1
P33 练习
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
