专题07 三角形的有关计算与证明 课件(共84张PPT)-2024年中考数学二轮复习讲练测(浙江新中考专用)
文档属性
| 名称 | 专题07 三角形的有关计算与证明 课件(共84张PPT)-2024年中考数学二轮复习讲练测(浙江新中考专用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览









文档简介
(共84张PPT)
专题07
三角形的有关计算与证明
2024年中考数学二轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
考点要求 命题预测
三角形的基础 近几年浙江省数学中考中,三角形相关的考查主要集中在三角形的性质、三角形的边角关系、三角形的全等和相似等方面。选择题和填空题主要考查学生对三角形基本性质和定理的理解和应用,而解答题则更注重对学生综合应用能力和解题技巧的考查,同时,题目中也经常出现一些需要结合其他知识点进行综合应用的情况,增加了题目的难度和复杂性。因此,在备考过程中,学生需要充分理解三角形的性质和定理,熟练掌握相关的计算方法和证明技巧,同时还需要注重培养自己的逻辑思维能力和空间想象能力。
特殊三角形的性质与判定 相似三角形
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
考点一 三角形的基础
考点一 三角形的基础
C
8
B
题型01 三角形的三边关系
提分笔记
1. 三角形三边关系定理及推论:
(1)定理:三角形的两边之和大于第三边.
(2)推论:三角形的两边之差小于第三边.
2. 解题技巧:
(1)判断三条已知线段能否组成三角形,只需检验最短的两边之和大于第三边,则可说明能组成三角形.
(2)若三角形两边的长度分别为a,b,则第三边的长度范围为:|a-b|(3)所有通过周长相加减求三角形的边,求出两个答案的,要注意检查每个答案能否组成三角形.
题型01 三角形的三边关系
A
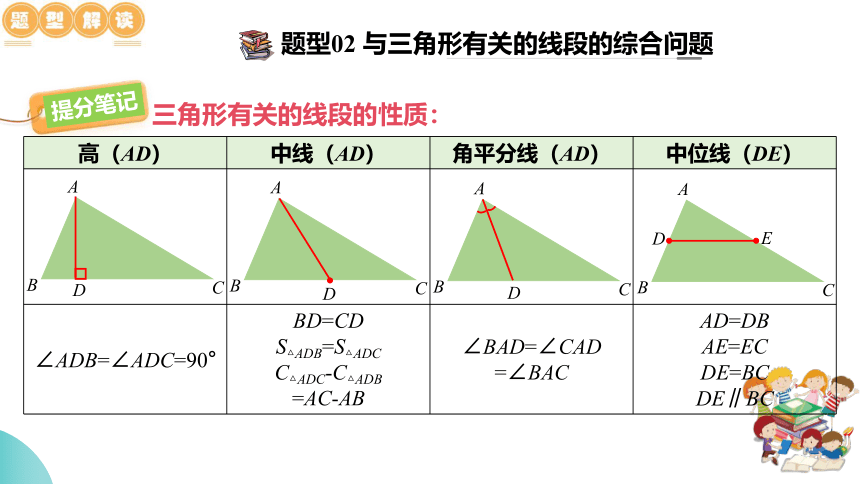
题型02 与三角形有关的线段的综合问题
提分笔记
三角形有关的线段的性质:
高(AD) 中线(AD) 角平分线(AD) 中位线(DE)
∠ADB=∠ADC=90° BD=CD S△ADB=S△ADC C△ADC-C△ADB =AC-AB ∠BAD=∠CAD =∠BAC AD=DB
AE=EC
DE=BC
DE∥BC
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
D
题型02 与三角形有关的线段的综合问题
B
A
题型03 三角形内角和定理与外角和定理综合问题
提分笔记
1. 三角形的内角和定理及推论:
(1)定理:三角形三个内角和等于180°.(2)推论:直角三角形的两个锐角互余.
(1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数.
(2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数.
(3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数.
2. 三角形的内角和定理的应用:
3. 三角形的外角和定理及性质:
(1)定理:三角形的外角和等于360°.
(2)性质:①三角形的一个外角等于和它不相邻的两个内角的和;
②三角形的一个外角大于任何一个和它不相邻的内角.
题型03 三角形内角和定理与外角和定理综合问题
D
题型03 三角形内角和定理与外角和定理综合问题
B
题型03 三角形内角和定理与外角和定理综合问题
题型03 三角形内角和定理与外角和定理综合问题
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
4
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
5a+5b=7c
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
F
H
G
A
题型01 线段垂直平分线的性质与判定
提分笔记
1. 垂直平分线的概念:
过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线).
2. 垂直平分线的性质与判定:
(1)性质:线段的垂直平分线上的点到这条线段两个端点的距离相等.
(2)判定:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
3. 解题技巧:
对于含有垂直平分线的题目,首先考虑将垂直平分线上的点与线段两端点连接起来.
题型01 线段垂直平分线的性质与判定
A
A
题型01 线段垂直平分线的性质与判定
A
题型02 角平分线的性质与判定
提分笔记
1. 垂直平分线的性质定理与判定定理:
(1)性质:角的平分线上的点到这个角的两边的距离相等.
(2)判定:角的内部,与角的两边的距离相等的点在这个角的平分线上.
2. 解题技巧:
看到角平分线的题目,可考虑作“两垂线”.
题型02 角平分线的性质与判定
C
F
G
题型02 角平分线的性质与判定
E
D
题型03 等腰三角形的性质与判定
提分笔记
等腰三角形的性质与判定:
(1)性质:
①等腰三角形的两个底角相等(简称“等边对等角”);
②等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”).
(2)判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称“等角对等边”).
题型03 等腰三角形的性质与判定
D
题型03 等腰三角形的性质与判定
题型04 等边三角形的性质与判定
提分笔记
等边三角形的性质与判定:
(1)性质:
①等边三角形的三条边相等;
②三个内角都相等,并且每个内角都是60°.
(2)判定:
①三边相等或三个内角都相等的三角形是等边三角形;
②有一个角是60°的等腰三角形是等边三角形.
题型04 等边三角形的性质与判定
B
题型04 等边三角形的性质与判定
题型04 等边三角形的性质与判定
题型05 全等三角形的性质与判定
提分笔记
1. 判定两个三角形全等常用的思路方法如下:
题型05 全等三角形的性质与判定
提分笔记
2. 找等角的常用方法证三角形全等时,常见的隐含等角有:
(1)公共角.
(2)对顶角相等.
(3)等角加(或减)等角仍得等角.
(4)角平分线得两等角.
(5)同角(或等角)的余角或补角相等.
(6)平行线得同位角、内错角相等.
(7)垂直定义得两角相等.
(8)一些自然规律:“太阳光线可以看作是平行线”“光的入射角等于反射角”等也是常见的隐含条件.
题型05 全等三角形的性质与判定
提分笔记
3. 根据对应顶点的字母写在对应位置上准确确定出全等三角形的对应边和对应角是解题关键.
(1)全等三角形性质的应用:可用来证明两条线段相等,两个角相等.
(2)平移、折叠、旋转属于全等变换,都能产生全等图形,利用全等的性质得到对应边相等、对应角相等解决问题.
4. 全等三角形的性质:
题型05 全等三角形的性质与判定
B
题型05 全等三角形的性质与判定
C
题型05 全等三角形的性质与判定
题型05 全等三角形的性质与判定
题型06 勾股定理﹑勾股定理逆定理与网格问题
提分笔记
1. 已知直角三角形的两边长,求第三边长,关键是先明确所求边是斜边还是直角边,再决定用勾股定理的原式还是变式.
2. 勾股定理的证明是通过拼图法或割补法完成的,探索时利用面积关系,将“形”的问题转化为“数”的问题.
3. 勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,因而在应用勾股定理时,必须明了所考察的对象是直角三角形.
4. 利用勾股定理解应用题的关键是寻找直角三角形,若不存在直角三角形,可通过添加辅助线构造出直角三角形.
题型06 勾股定理﹑勾股定理逆定理与网格问题
提分笔记
5. 利用勾股定理的逆定理判断一个三角形是不是直角三角形的一般步骤:
(1)确定三角形的最长边.(2)分别计算出最长边的平方与另两边的平方和.
(3)通过比较来判断最长边的平方与另两边的平方和是否相等.
(4)作出结论,若相等,则说明这个三角形是直角三角形,否则不是直角三角形.
6. 勾股数
(1)常见的勾股数有:
①3,4,5;②6,8,10;③8,15,17;④7,24,25;⑤5,12,13;⑥9,12,15.
常见的勾股数需牢记,平时在解决问题时常用,有利于打开思路.
(2)用含字母n的代数式表示组勾股数:n2-1,2n,n2+1(n≥2,n为正整数).
题型06 勾股定理﹑勾股定理逆定理与网格问题
C
题型06 勾股定理﹑勾股定理逆定理与网格问题
题型07 赵爽弦图
提分笔记
赵爽弦图的几何意义:
(1)证明勾股定理:c2=a2+b2.
(2)IJ=b-a.
(3)S正方形EFGH=c2=a2+b2,S正方形IJKL=(b-a)2.
(4)S阴影= S正方形EFGH- S正方形IJKL=2ab.
题型07 赵爽弦图
C
题型08 利用勾股定理解决实际问题
提分笔记
利用勾股定理解决实际问题的一般步骤:
(1)将实际问题转化为数学问题.
(2)明确已知条件及结论.
(3)利用勾股定理解答,并确定实际问题的答案.
题型08 利用勾股定理解决实际问题
14
题型08 利用勾股定理解决实际问题
题型08 利用勾股定理解决实际问题
题型08 利用勾股定理解决实际问题
考点三 相似三角形
考点三 相似三角形
C
考点三 相似三角形
M
T
9
考点三 相似三角形
T
考点三 相似三角形
考点三 相似三角形
N
N
考点三 相似三角形
考点三 相似三角形
题型01 比例线段
提分笔记
1. 比例:如果两个数的比值与另两个数的比值相等,就说这四个数成比例,通常我们把a,b,c,d四个实数成比例表示成或者a:b=c:d,其中b,c称为比例内项,a,d称为比例外项.
等式两边同乘以bd,可得ad=bc,反过来等式ad=bc同除以bd,可得.
2. 比例线段:在四条线段a,b,c,d中,如果a和b的比等于c和d的比,即,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
题型01 比例线段
提分笔记
3. 比例中项:如果三个数a,b,c满足比例式,那么b叫做a、c的比例中项, 此时有b2=ac.
4. 黄金分割:如果点P把线段AB分成两条线段AP和PB,使,那么称线段AB被点P黄金分割,点P叫做线段的黄金分割点,比值叫做黄金比.≈.
5. 比例式变形:;.
题型01 比例线段
D
D
4
题型01 比例线段
题型02 相似三角形的性质和判定
提分笔记
1. 判定定理:
判定定理1:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
判定定理2:三边成比例的两个三角形相似.
判定定理3:两边成比例且夹角相等的两个三角形相似.
判定定理4:两角分别相等的两个三角形相似.
2. 判定三角形相似的几条思路:
(1)条件中若有平行线,可采用相似三角形的判定定理1;
(2)条件中若有一对等角,可再找一对等角[用判定定理1]
或再找夹边成比例[用判定定理2];
(3)条件中若有两边对应成比例,可找夹角相等;
(4)条件中若有一对直角,可考虑再找一对等角或证明斜边、直角边对应成比例;
(5)条件中若有等腰条件,可找顶角相等,或找一个底角相等,也可找底和腰对应成比例.
题型02 相似三角形的性质和判定
提分笔记
3. 性质定理:
(1)相似三角形对应角相等,对应边成比例.
(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(3)相似三角形周长的比等于相似比.
(4)相似三角形面积的比等于相似比的平方.
题型02 相似三角形的性质和判定
B
A
B
题型02 相似三角形的性质和判定
C
题型02 相似三角形的性质和判定
题型02 相似三角形的性质和判定
题型03 相似三角形的实际应用
提分笔记
1. 利用投影、平行线、标杆等构造相似三角形求解.
2. 测量底部可以到达的物体的高度.
3. 测量底部不可以到达的物体的高度.
4. 测量河的宽度.
题型03 相似三角形的实际应用
B
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
5
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
感谢观看
THANK YOU
专题07
三角形的有关计算与证明
2024年中考数学二轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
考点要求 命题预测
三角形的基础 近几年浙江省数学中考中,三角形相关的考查主要集中在三角形的性质、三角形的边角关系、三角形的全等和相似等方面。选择题和填空题主要考查学生对三角形基本性质和定理的理解和应用,而解答题则更注重对学生综合应用能力和解题技巧的考查,同时,题目中也经常出现一些需要结合其他知识点进行综合应用的情况,增加了题目的难度和复杂性。因此,在备考过程中,学生需要充分理解三角形的性质和定理,熟练掌握相关的计算方法和证明技巧,同时还需要注重培养自己的逻辑思维能力和空间想象能力。
特殊三角形的性质与判定 相似三角形
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
考点一 三角形的基础
考点一 三角形的基础
C
8
B
题型01 三角形的三边关系
提分笔记
1. 三角形三边关系定理及推论:
(1)定理:三角形的两边之和大于第三边.
(2)推论:三角形的两边之差小于第三边.
2. 解题技巧:
(1)判断三条已知线段能否组成三角形,只需检验最短的两边之和大于第三边,则可说明能组成三角形.
(2)若三角形两边的长度分别为a,b,则第三边的长度范围为:|a-b|
题型01 三角形的三边关系
A
题型02 与三角形有关的线段的综合问题
提分笔记
三角形有关的线段的性质:
高(AD) 中线(AD) 角平分线(AD) 中位线(DE)
∠ADB=∠ADC=90° BD=CD S△ADB=S△ADC C△ADC-C△ADB =AC-AB ∠BAD=∠CAD =∠BAC AD=DB
AE=EC
DE=BC
DE∥BC
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
D
题型02 与三角形有关的线段的综合问题
B
A
题型03 三角形内角和定理与外角和定理综合问题
提分笔记
1. 三角形的内角和定理及推论:
(1)定理:三角形三个内角和等于180°.(2)推论:直角三角形的两个锐角互余.
(1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数.
(2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数.
(3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数.
2. 三角形的内角和定理的应用:
3. 三角形的外角和定理及性质:
(1)定理:三角形的外角和等于360°.
(2)性质:①三角形的一个外角等于和它不相邻的两个内角的和;
②三角形的一个外角大于任何一个和它不相邻的内角.
题型03 三角形内角和定理与外角和定理综合问题
D
题型03 三角形内角和定理与外角和定理综合问题
B
题型03 三角形内角和定理与外角和定理综合问题
题型03 三角形内角和定理与外角和定理综合问题
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
4
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
5a+5b=7c
考点二 特殊三角形的性质与判定
考点二 特殊三角形的性质与判定
F
H
G
A
题型01 线段垂直平分线的性质与判定
提分笔记
1. 垂直平分线的概念:
过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线).
2. 垂直平分线的性质与判定:
(1)性质:线段的垂直平分线上的点到这条线段两个端点的距离相等.
(2)判定:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
3. 解题技巧:
对于含有垂直平分线的题目,首先考虑将垂直平分线上的点与线段两端点连接起来.
题型01 线段垂直平分线的性质与判定
A
A
题型01 线段垂直平分线的性质与判定
A
题型02 角平分线的性质与判定
提分笔记
1. 垂直平分线的性质定理与判定定理:
(1)性质:角的平分线上的点到这个角的两边的距离相等.
(2)判定:角的内部,与角的两边的距离相等的点在这个角的平分线上.
2. 解题技巧:
看到角平分线的题目,可考虑作“两垂线”.
题型02 角平分线的性质与判定
C
F
G
题型02 角平分线的性质与判定
E
D
题型03 等腰三角形的性质与判定
提分笔记
等腰三角形的性质与判定:
(1)性质:
①等腰三角形的两个底角相等(简称“等边对等角”);
②等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”).
(2)判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称“等角对等边”).
题型03 等腰三角形的性质与判定
D
题型03 等腰三角形的性质与判定
题型04 等边三角形的性质与判定
提分笔记
等边三角形的性质与判定:
(1)性质:
①等边三角形的三条边相等;
②三个内角都相等,并且每个内角都是60°.
(2)判定:
①三边相等或三个内角都相等的三角形是等边三角形;
②有一个角是60°的等腰三角形是等边三角形.
题型04 等边三角形的性质与判定
B
题型04 等边三角形的性质与判定
题型04 等边三角形的性质与判定
题型05 全等三角形的性质与判定
提分笔记
1. 判定两个三角形全等常用的思路方法如下:
题型05 全等三角形的性质与判定
提分笔记
2. 找等角的常用方法证三角形全等时,常见的隐含等角有:
(1)公共角.
(2)对顶角相等.
(3)等角加(或减)等角仍得等角.
(4)角平分线得两等角.
(5)同角(或等角)的余角或补角相等.
(6)平行线得同位角、内错角相等.
(7)垂直定义得两角相等.
(8)一些自然规律:“太阳光线可以看作是平行线”“光的入射角等于反射角”等也是常见的隐含条件.
题型05 全等三角形的性质与判定
提分笔记
3. 根据对应顶点的字母写在对应位置上准确确定出全等三角形的对应边和对应角是解题关键.
(1)全等三角形性质的应用:可用来证明两条线段相等,两个角相等.
(2)平移、折叠、旋转属于全等变换,都能产生全等图形,利用全等的性质得到对应边相等、对应角相等解决问题.
4. 全等三角形的性质:
题型05 全等三角形的性质与判定
B
题型05 全等三角形的性质与判定
C
题型05 全等三角形的性质与判定
题型05 全等三角形的性质与判定
题型06 勾股定理﹑勾股定理逆定理与网格问题
提分笔记
1. 已知直角三角形的两边长,求第三边长,关键是先明确所求边是斜边还是直角边,再决定用勾股定理的原式还是变式.
2. 勾股定理的证明是通过拼图法或割补法完成的,探索时利用面积关系,将“形”的问题转化为“数”的问题.
3. 勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,因而在应用勾股定理时,必须明了所考察的对象是直角三角形.
4. 利用勾股定理解应用题的关键是寻找直角三角形,若不存在直角三角形,可通过添加辅助线构造出直角三角形.
题型06 勾股定理﹑勾股定理逆定理与网格问题
提分笔记
5. 利用勾股定理的逆定理判断一个三角形是不是直角三角形的一般步骤:
(1)确定三角形的最长边.(2)分别计算出最长边的平方与另两边的平方和.
(3)通过比较来判断最长边的平方与另两边的平方和是否相等.
(4)作出结论,若相等,则说明这个三角形是直角三角形,否则不是直角三角形.
6. 勾股数
(1)常见的勾股数有:
①3,4,5;②6,8,10;③8,15,17;④7,24,25;⑤5,12,13;⑥9,12,15.
常见的勾股数需牢记,平时在解决问题时常用,有利于打开思路.
(2)用含字母n的代数式表示组勾股数:n2-1,2n,n2+1(n≥2,n为正整数).
题型06 勾股定理﹑勾股定理逆定理与网格问题
C
题型06 勾股定理﹑勾股定理逆定理与网格问题
题型07 赵爽弦图
提分笔记
赵爽弦图的几何意义:
(1)证明勾股定理:c2=a2+b2.
(2)IJ=b-a.
(3)S正方形EFGH=c2=a2+b2,S正方形IJKL=(b-a)2.
(4)S阴影= S正方形EFGH- S正方形IJKL=2ab.
题型07 赵爽弦图
C
题型08 利用勾股定理解决实际问题
提分笔记
利用勾股定理解决实际问题的一般步骤:
(1)将实际问题转化为数学问题.
(2)明确已知条件及结论.
(3)利用勾股定理解答,并确定实际问题的答案.
题型08 利用勾股定理解决实际问题
14
题型08 利用勾股定理解决实际问题
题型08 利用勾股定理解决实际问题
题型08 利用勾股定理解决实际问题
考点三 相似三角形
考点三 相似三角形
C
考点三 相似三角形
M
T
9
考点三 相似三角形
T
考点三 相似三角形
考点三 相似三角形
N
N
考点三 相似三角形
考点三 相似三角形
题型01 比例线段
提分笔记
1. 比例:如果两个数的比值与另两个数的比值相等,就说这四个数成比例,通常我们把a,b,c,d四个实数成比例表示成或者a:b=c:d,其中b,c称为比例内项,a,d称为比例外项.
等式两边同乘以bd,可得ad=bc,反过来等式ad=bc同除以bd,可得.
2. 比例线段:在四条线段a,b,c,d中,如果a和b的比等于c和d的比,即,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
题型01 比例线段
提分笔记
3. 比例中项:如果三个数a,b,c满足比例式,那么b叫做a、c的比例中项, 此时有b2=ac.
4. 黄金分割:如果点P把线段AB分成两条线段AP和PB,使,那么称线段AB被点P黄金分割,点P叫做线段的黄金分割点,比值叫做黄金比.≈.
5. 比例式变形:;.
题型01 比例线段
D
D
4
题型01 比例线段
题型02 相似三角形的性质和判定
提分笔记
1. 判定定理:
判定定理1:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
判定定理2:三边成比例的两个三角形相似.
判定定理3:两边成比例且夹角相等的两个三角形相似.
判定定理4:两角分别相等的两个三角形相似.
2. 判定三角形相似的几条思路:
(1)条件中若有平行线,可采用相似三角形的判定定理1;
(2)条件中若有一对等角,可再找一对等角[用判定定理1]
或再找夹边成比例[用判定定理2];
(3)条件中若有两边对应成比例,可找夹角相等;
(4)条件中若有一对直角,可考虑再找一对等角或证明斜边、直角边对应成比例;
(5)条件中若有等腰条件,可找顶角相等,或找一个底角相等,也可找底和腰对应成比例.
题型02 相似三角形的性质和判定
提分笔记
3. 性质定理:
(1)相似三角形对应角相等,对应边成比例.
(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(3)相似三角形周长的比等于相似比.
(4)相似三角形面积的比等于相似比的平方.
题型02 相似三角形的性质和判定
B
A
B
题型02 相似三角形的性质和判定
C
题型02 相似三角形的性质和判定
题型02 相似三角形的性质和判定
题型03 相似三角形的实际应用
提分笔记
1. 利用投影、平行线、标杆等构造相似三角形求解.
2. 测量底部可以到达的物体的高度.
3. 测量底部不可以到达的物体的高度.
4. 测量河的宽度.
题型03 相似三角形的实际应用
B
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
5
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
题型03 相似三角形的实际应用
感谢观看
THANK YOU
同课章节目录
