专题08 特殊平行四边形的计算与证明 课件(共43张PPT)-2024年中考数学二轮复习讲练测(浙江新中考专用)
文档属性
| 名称 | 专题08 特殊平行四边形的计算与证明 课件(共43张PPT)-2024年中考数学二轮复习讲练测(浙江新中考专用) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:20:57 | ||
图片预览










文档简介
(共43张PPT)
专题08
特殊平行四边形的计算与证明
2024年中考数学二轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
考点要求 命题预测
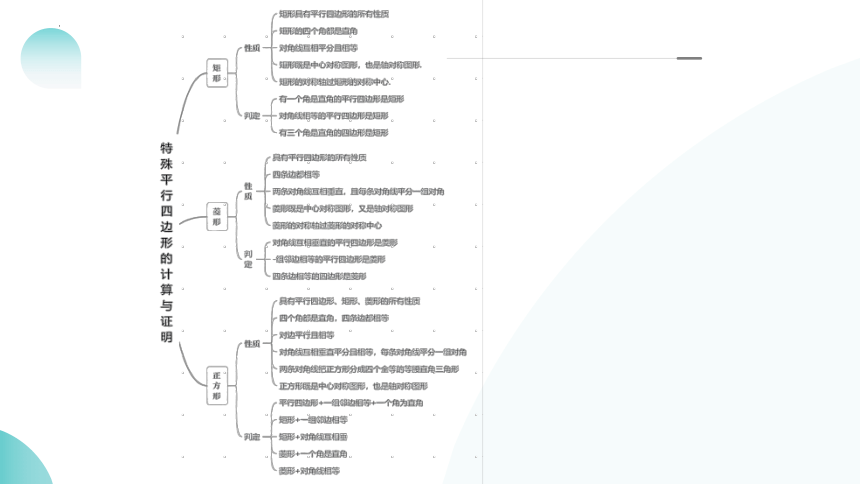
特殊平行四边形 特殊平行四边形是矩形、菱形、正方形的合集,在浙江中考中通常以综合题出现,其中,矩形还经常成为综合压轴题的问题背景来考察,矩形其他出题类型还有选择、填空题的压轴题,难度都比较大,需要加以重视。菱形的考察类型也比较多样,选择、填空题常考察菱形的基本性质,综合题中也常以压轴题出现。正方形整体考察的较少,但是出现时也基本都是选择题的压轴题,难度也较大。所以考生在这块知识点的复习上,必须都要特别的重视,熟练掌握特殊平行四边的性质与判定,以及其应用。
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
考点一 特殊平行四边形
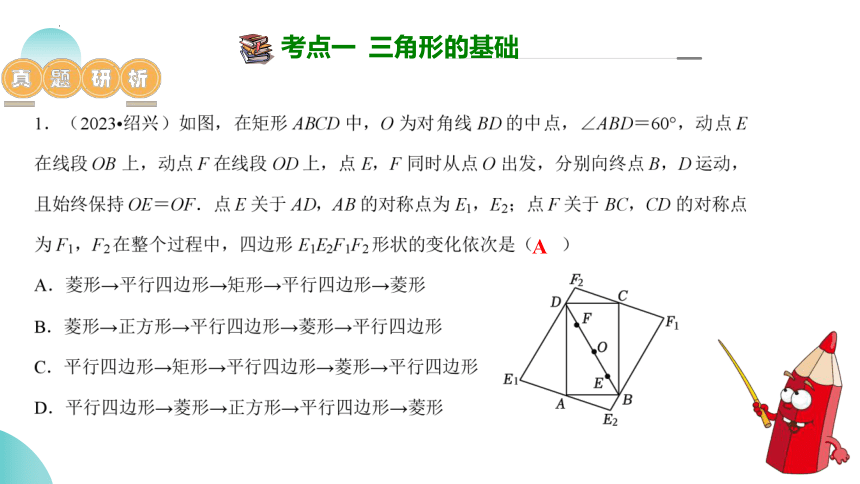
考点一 三角形的基础
A
考点一 三角形的基础
考点一 三角形的基础
4
考点一 三角形的基础
考点一 三角形的基础
O
考点一 三角形的基础
考点一 三角形的基础
考点一 三角形的基础
题型01 利用矩形的性质与判定求解
提分笔记
1. 矩形的性质:
(1)矩形的定义:有一个角是直角的平行四边形叫矩形,矩形是特殊的平行四边形.
(2)矩形的性质:①具有平行四边形的性质;②对角线相等;③四个角都是直角.
注意:矩形是轴对称图形,有两条对称轴.
2. 直角三角形斜边上的中线等于斜边的一半
(1)有一个内角是直角的平行四边形叫矩形(根据定义).
(2)对角线相等的平行四边形是矩形.
(3)四个角都相等的四边形是矩形.
3. 矩形的判定:
题型01 利用矩形的性质与判定求解
C
题型01 利用矩形的性质与判定求解
M
N
C
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
矩形(正方形)的折叠问题的常用解题思路:
(1)对折叠前后的图形进行细致分析,折叠后的图形与原图形全等,对应边、对应角分别相等,找出各相等的边或角.
(2)折痕可看作角平分线(对称线段所在的直线与折痕的夹角相等).
(3)折痕可看作垂直平分线(互相重合的两点之间的连线被折痕垂直平分).
(4)选择一个直角三角形(不找以折痕为边长的直角三角形),利用未知数表示其它直角三角形三边,通过勾股定理/相似三角形知识求解.
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
题型02 与矩形(或正方形)有关的折叠问题
题型02 与矩形(或正方形)有关的折叠问题
题型02 与矩形(或正方形)有关的折叠问题
题型03 根据矩形的性质与判定解决多结论问题
题型03 根据矩形的性质与判定解决多结论问题
题型04 根据菱形的性质与判定求解
提分笔记
1. 菱形的性质:
(1)菱形的定义:一组邻边相等的平行四边形叫做菱形.
(2)菱形的性质:①具有平行四边形的性质;②四条边都相等;③两条对角线互相垂直平分,每一条对角线平分一组对角.
注意:菱形是轴对称图形,每条对角线所在的直线都是对称轴.
(1)一组邻边相等的平行四边形是菱形.
(2)对角线互相垂直的平行四边形是菱形.
(3)四条边都相等的四边形是菱形.
2. 菱形的判定:
3. 菱形的面积:
菱形的面积等于两条对角线长的乘积的一半.
题型04 根据菱形的性质与判定求解
E
F
12-6
题型04 根据菱形的性质与判定求解
题型04 根据菱形的性质与判定求解
题型04 根据菱形的性质与判定求解
题型05 根据正方形的性质与判定求解
提分笔记
1. 正方形的概念与性质:
(1)正方形的定义:一组邻边相等的矩形叫做正方形.
(2)正方形的性质:正方形具有平行四边形、矩形、菱形的一切性质.
注意:正方形是轴对称图形,有四条对称轴.
2. 正方形的判定:
(1)有一个内角是直角的菱形是正方形.
(2)邻边相等的矩形是正方形.
(3)对角线相等的菱形是正方形.
(4)对角线互相垂直的矩形是正方形.
题型05 根据正方形的性质与判定求解
题型05 根据正方形的性质与判定求解
H
题型05 根据正方形的性质与判定求解
H
题型05 根据正方形的性质与判定求解
题型06 正方形与函数的相关问题
C
题型07 与特殊四边形有关的新定义问题
D
题型07 与特殊四边形有关的新定义问题
H
F
E
题型07 与特殊四边形有关的新定义问题
感谢观看
THANK YOU
专题08
特殊平行四边形的计算与证明
2024年中考数学二轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
考点要求 命题预测
特殊平行四边形 特殊平行四边形是矩形、菱形、正方形的合集,在浙江中考中通常以综合题出现,其中,矩形还经常成为综合压轴题的问题背景来考察,矩形其他出题类型还有选择、填空题的压轴题,难度都比较大,需要加以重视。菱形的考察类型也比较多样,选择、填空题常考察菱形的基本性质,综合题中也常以压轴题出现。正方形整体考察的较少,但是出现时也基本都是选择题的压轴题,难度也较大。所以考生在这块知识点的复习上,必须都要特别的重视,熟练掌握特殊平行四边的性质与判定,以及其应用。
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
考点一 特殊平行四边形
考点一 三角形的基础
A
考点一 三角形的基础
考点一 三角形的基础
4
考点一 三角形的基础
考点一 三角形的基础
O
考点一 三角形的基础
考点一 三角形的基础
考点一 三角形的基础
题型01 利用矩形的性质与判定求解
提分笔记
1. 矩形的性质:
(1)矩形的定义:有一个角是直角的平行四边形叫矩形,矩形是特殊的平行四边形.
(2)矩形的性质:①具有平行四边形的性质;②对角线相等;③四个角都是直角.
注意:矩形是轴对称图形,有两条对称轴.
2. 直角三角形斜边上的中线等于斜边的一半
(1)有一个内角是直角的平行四边形叫矩形(根据定义).
(2)对角线相等的平行四边形是矩形.
(3)四个角都相等的四边形是矩形.
3. 矩形的判定:
题型01 利用矩形的性质与判定求解
C
题型01 利用矩形的性质与判定求解
M
N
C
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
矩形(正方形)的折叠问题的常用解题思路:
(1)对折叠前后的图形进行细致分析,折叠后的图形与原图形全等,对应边、对应角分别相等,找出各相等的边或角.
(2)折痕可看作角平分线(对称线段所在的直线与折痕的夹角相等).
(3)折痕可看作垂直平分线(互相重合的两点之间的连线被折痕垂直平分).
(4)选择一个直角三角形(不找以折痕为边长的直角三角形),利用未知数表示其它直角三角形三边,通过勾股定理/相似三角形知识求解.
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
题型02 与矩形(或正方形)有关的折叠问题
提分笔记
题型02 与矩形(或正方形)有关的折叠问题
题型02 与矩形(或正方形)有关的折叠问题
题型02 与矩形(或正方形)有关的折叠问题
题型03 根据矩形的性质与判定解决多结论问题
题型03 根据矩形的性质与判定解决多结论问题
题型04 根据菱形的性质与判定求解
提分笔记
1. 菱形的性质:
(1)菱形的定义:一组邻边相等的平行四边形叫做菱形.
(2)菱形的性质:①具有平行四边形的性质;②四条边都相等;③两条对角线互相垂直平分,每一条对角线平分一组对角.
注意:菱形是轴对称图形,每条对角线所在的直线都是对称轴.
(1)一组邻边相等的平行四边形是菱形.
(2)对角线互相垂直的平行四边形是菱形.
(3)四条边都相等的四边形是菱形.
2. 菱形的判定:
3. 菱形的面积:
菱形的面积等于两条对角线长的乘积的一半.
题型04 根据菱形的性质与判定求解
E
F
12-6
题型04 根据菱形的性质与判定求解
题型04 根据菱形的性质与判定求解
题型04 根据菱形的性质与判定求解
题型05 根据正方形的性质与判定求解
提分笔记
1. 正方形的概念与性质:
(1)正方形的定义:一组邻边相等的矩形叫做正方形.
(2)正方形的性质:正方形具有平行四边形、矩形、菱形的一切性质.
注意:正方形是轴对称图形,有四条对称轴.
2. 正方形的判定:
(1)有一个内角是直角的菱形是正方形.
(2)邻边相等的矩形是正方形.
(3)对角线相等的菱形是正方形.
(4)对角线互相垂直的矩形是正方形.
题型05 根据正方形的性质与判定求解
题型05 根据正方形的性质与判定求解
H
题型05 根据正方形的性质与判定求解
H
题型05 根据正方形的性质与判定求解
题型06 正方形与函数的相关问题
C
题型07 与特殊四边形有关的新定义问题
D
题型07 与特殊四边形有关的新定义问题
H
F
E
题型07 与特殊四边形有关的新定义问题
感谢观看
THANK YOU
同课章节目录
