人教版六年级数学下册 《正比例 》课件(共20张PPT)
文档属性
| 名称 | 人教版六年级数学下册 《正比例 》课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第1课时 :正比例
第四单元:比例
已知路程和时间,怎样求速度?
路程÷时间
已知总价和数量,怎样求单价?
总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作总量÷工作时间
文具店有一种彩带,销售的数量与总价的关系如下表。
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)总价是怎样随着数量的变化而变化的?
(3)相应的总价与数量的比分别是多少?比值是多少?
1、 两种相关联的量,一种量变化,另一种量也随着变化。
2、这两种量中相对应的两个数的比值一定。
3、这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
(一定)
如果汽车行驶速度一定,路程与时间成正比例关系。
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
已知路程和时间,求速度。
速度 = 路程÷时间
已知总价和数量,求单价。
单价 = 总价÷数量
已知工作总量和工作时间,求工作效率。
工作效率 = 工作总量÷工作时间
它们的关系是正比例关系
横轴表示什么?纵轴表示什么?
A
A点表示什么?
你能根据表中的每组数据,在方格中找出对应的点,并一次描出这些点吗?
表示1m彩带需要3.5元
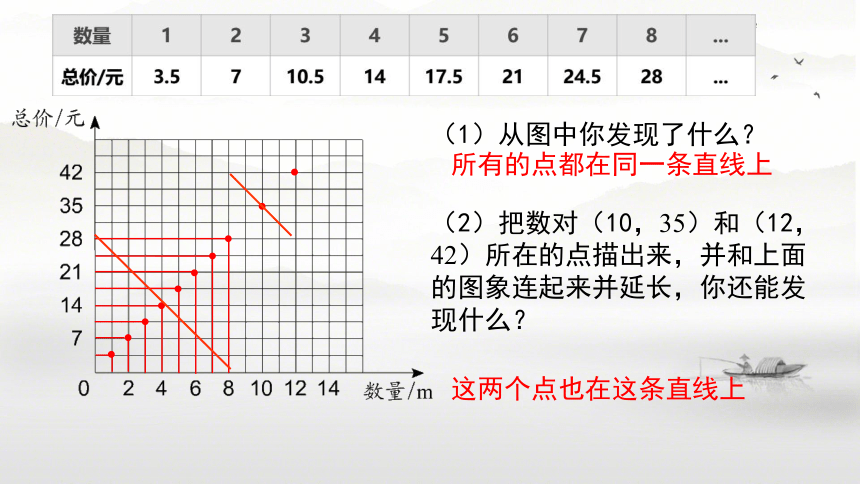
(1)从图中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么?
所有的点都在同一条直线上
这两个点也在这条直线上
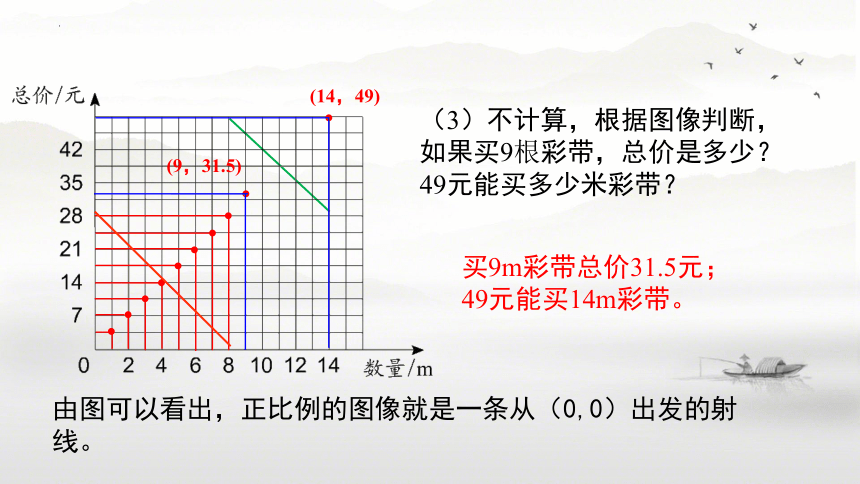
(3)不计算,根据图像判断,如果买9根彩带,总价是多少?49元能买多少米彩带?
(9,31.5)
(14,49)
买9m彩带总价31.5元;
49元能买14m彩带。
由图可以看出,正比例的图像就是一条从(0,0)出发的射线。
1.一辆汽车行驶的时间和路程如下表。
(1)写出几组路程与相对的时间的比,并比较比值的大小。
(2)说一说这个比值表示什么。
这个比值表示汽车行驶的速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
路程和时间成正比例关系;因为路程和时间对应的比值一定,都等于80。
120
1.5
行驶120km大约要用1.5小时。
(4)在图中描出表示路程和时间相对应的点,然后把它们按顺序连接起来。并估计一下行驶120km大约要用多少时间。
直线经过0点,那么0点表示什么意思呢?
思考
2.下面是小林家去年上半年每月用电量情况。
(1)分别写出各月电费与用电量的比,比较比值的大小。
60:120=65:130=55:110=60:120=65:130=75:150=0.5
(2)说明这个比值所表示的意义。
比值表示每千瓦时的电费。
(3)电费与相应的用电量成正比例关系?为什么?
成正比例关系,因为电费÷用电量=单价(一定),比值一定。
长沙造纸厂的生产情况如下表,根据表回答问题。
时间(天)
生产量(吨)
1
2
3
4
5
6
7
8
70
140
210
280
350
420
490
560
…
…
时间和生产量成正比例关系吗?
生产量
时间
=
每天生产的质量(一定)
所以 生产量和时间成正比例。
1. 表示x和y成正比例关系的式子是( )。
2. 甲数是乙数的2倍,甲数与乙数成( )关系。
正比例
如果两个数的商一定,那么这两个数就成正比例关系。
典题精讲
总价
质量
=
单价(一定)
所以购买苹果的质量和总价成正比例。
判断下面每题中的两种量是不是成正比例,并说明理由。
(1)苹果的单价一定,购买苹果的质量和总价。
苹果的质量和总价是两种相关联的量,
学以致用
判断下面每题中的两种量是不是成正比例,并说明由。
路程
时间
=
速度(一定)
所以行驶的路程和时间成正比例。
(2)轮船行驶的速度一定,行驶的路程和时间。
行驶的路程和时间是两种相关联的量,
学以致用
判断下面每题中的两种量是不是成正比例,并说明理由。
织布总长度
时间
=
每小时织布长度(一定)
所以织布总长度和时间成正比例。
(3)每小时织布长度一定,织布总长度和时间。
织布总长度和时间是两种相关联的量,
学以致用
判断下面每题中的两种量是不是成正比例,并说明理由。
所以 小新跳高的高度和他的身高不成正比例。
(4)小新跳高的高度和他的身高。
跳高的高度和身高不是两种相关联的量,
学以致用
成正比例的量的三要素:
①两种相关联的量。
②其中一个量增加,另一个量也增加;一个量减少,另一个量也减少。
③两个量的比值一定。
1.判断下面每组中的量是否成正比例关系。
(1)平行四边形的高一定,它的面积和底。
(2)小明的身高和体重。
(3)长方形的周长一定,长和宽。
(4)收入一定,支出和结余。
√
×
×
×
( )
( )
( )
( )
第1课时 :正比例
第四单元:比例
已知路程和时间,怎样求速度?
路程÷时间
已知总价和数量,怎样求单价?
总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作总量÷工作时间
文具店有一种彩带,销售的数量与总价的关系如下表。
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)总价是怎样随着数量的变化而变化的?
(3)相应的总价与数量的比分别是多少?比值是多少?
1、 两种相关联的量,一种量变化,另一种量也随着变化。
2、这两种量中相对应的两个数的比值一定。
3、这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
(一定)
如果汽车行驶速度一定,路程与时间成正比例关系。
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
已知路程和时间,求速度。
速度 = 路程÷时间
已知总价和数量,求单价。
单价 = 总价÷数量
已知工作总量和工作时间,求工作效率。
工作效率 = 工作总量÷工作时间
它们的关系是正比例关系
横轴表示什么?纵轴表示什么?
A
A点表示什么?
你能根据表中的每组数据,在方格中找出对应的点,并一次描出这些点吗?
表示1m彩带需要3.5元
(1)从图中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么?
所有的点都在同一条直线上
这两个点也在这条直线上
(3)不计算,根据图像判断,如果买9根彩带,总价是多少?49元能买多少米彩带?
(9,31.5)
(14,49)
买9m彩带总价31.5元;
49元能买14m彩带。
由图可以看出,正比例的图像就是一条从(0,0)出发的射线。
1.一辆汽车行驶的时间和路程如下表。
(1)写出几组路程与相对的时间的比,并比较比值的大小。
(2)说一说这个比值表示什么。
这个比值表示汽车行驶的速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
路程和时间成正比例关系;因为路程和时间对应的比值一定,都等于80。
120
1.5
行驶120km大约要用1.5小时。
(4)在图中描出表示路程和时间相对应的点,然后把它们按顺序连接起来。并估计一下行驶120km大约要用多少时间。
直线经过0点,那么0点表示什么意思呢?
思考
2.下面是小林家去年上半年每月用电量情况。
(1)分别写出各月电费与用电量的比,比较比值的大小。
60:120=65:130=55:110=60:120=65:130=75:150=0.5
(2)说明这个比值所表示的意义。
比值表示每千瓦时的电费。
(3)电费与相应的用电量成正比例关系?为什么?
成正比例关系,因为电费÷用电量=单价(一定),比值一定。
长沙造纸厂的生产情况如下表,根据表回答问题。
时间(天)
生产量(吨)
1
2
3
4
5
6
7
8
70
140
210
280
350
420
490
560
…
…
时间和生产量成正比例关系吗?
生产量
时间
=
每天生产的质量(一定)
所以 生产量和时间成正比例。
1. 表示x和y成正比例关系的式子是( )。
2. 甲数是乙数的2倍,甲数与乙数成( )关系。
正比例
如果两个数的商一定,那么这两个数就成正比例关系。
典题精讲
总价
质量
=
单价(一定)
所以购买苹果的质量和总价成正比例。
判断下面每题中的两种量是不是成正比例,并说明理由。
(1)苹果的单价一定,购买苹果的质量和总价。
苹果的质量和总价是两种相关联的量,
学以致用
判断下面每题中的两种量是不是成正比例,并说明由。
路程
时间
=
速度(一定)
所以行驶的路程和时间成正比例。
(2)轮船行驶的速度一定,行驶的路程和时间。
行驶的路程和时间是两种相关联的量,
学以致用
判断下面每题中的两种量是不是成正比例,并说明理由。
织布总长度
时间
=
每小时织布长度(一定)
所以织布总长度和时间成正比例。
(3)每小时织布长度一定,织布总长度和时间。
织布总长度和时间是两种相关联的量,
学以致用
判断下面每题中的两种量是不是成正比例,并说明理由。
所以 小新跳高的高度和他的身高不成正比例。
(4)小新跳高的高度和他的身高。
跳高的高度和身高不是两种相关联的量,
学以致用
成正比例的量的三要素:
①两种相关联的量。
②其中一个量增加,另一个量也增加;一个量减少,另一个量也减少。
③两个量的比值一定。
1.判断下面每组中的量是否成正比例关系。
(1)平行四边形的高一定,它的面积和底。
(2)小明的身高和体重。
(3)长方形的周长一定,长和宽。
(4)收入一定,支出和结余。
√
×
×
×
( )
( )
( )
( )
