平行线的性质
图片预览





文档简介
课件18张PPT。5.3 平行线的性质复习回顾一下!问题1:判定两条直线平行,我们学过的方法有哪几种?方法1:同位角相等,两直线平行.方法2:内错角相等,两直线平行.方法3:同旁内角互补,两直线平行.方法4:如果两条直线都与第三条直线平行。
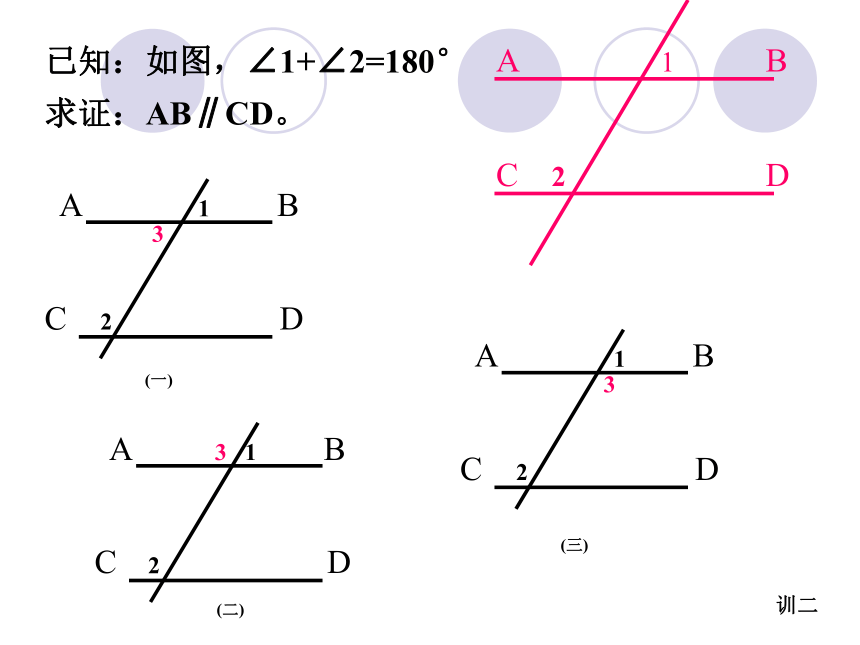
那么这两条直线也互相平行.方法5:同垂直一条直线的两条直线互相平行已知:如图,∠1+∠2=180°
求证:AB∥CD。(一)(二)(三)训二问题2:根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢?内错角,同旁内角之间又有什么关系呢?
动手画一画! (1)用直尺和三角尺画出两条平行线 a∥b,再画一条截线c,使之与直线 a,b相交,并标出所形成的八个角.
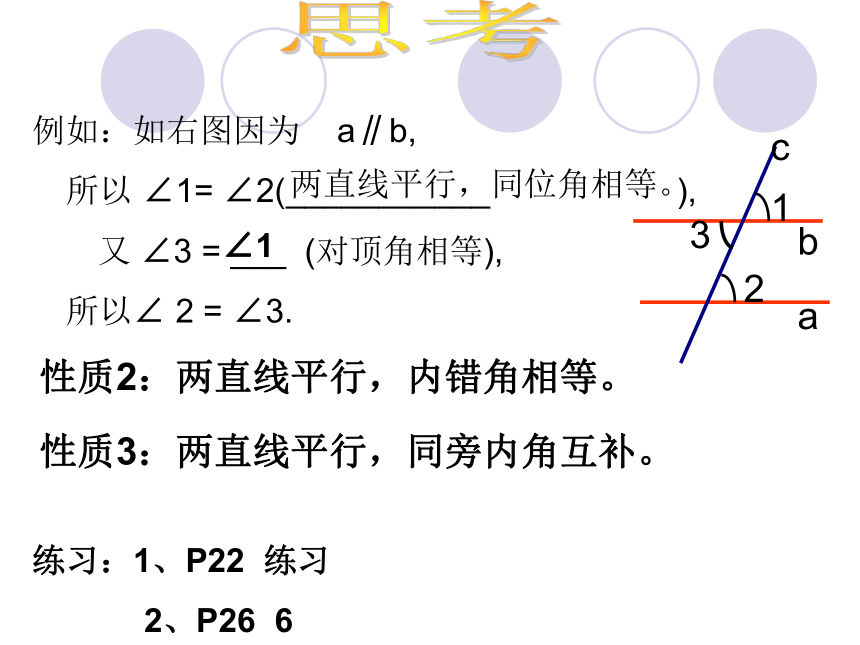
(2)测量上面八个角的大小,记录下来.从中你能发现什么?性质1:两直线平行,同位角相等.平行线的性质:思考例如:如右图因为 a∥b,
所以 ∠1= ∠2(___________ ),
又 ∠3 = ___ (对顶角相等),
所以∠ 2 = ∠3.两直线平行,同位角相等。∠1练习:1、P22 练习
2、P26 6性质2:两直线平行,内错角相等。性质3:两直线平行,同旁内角互补。图形已知结果结论同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc平行线的判定小结a//b同位角相等
两直线平行a//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行平行线的性质你能区别平行线的判定与性质吗?判定性质平行线的判定是先知道角相等或互补,后知道两直线平行。平行线的性质是先知道两直线平行,后知道角相等或互补。平行线的判定与平行线 的性质的比较:平行线的判定与平行线的性质是因果互换的两类不同的定理,判定是说:满足了什么条件(性质)的两条直线是互相平行的性质是说:如果两条直线平行,就应该具有什么性质。例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯
形上底的一部分(如图)。要订造一块新的玻璃,已经
量得 ,你想一想,梯形另外两个角
各是多少度?解:因为梯形上.下底互相平行,所以
梯形的另外两个 角分别是ADBC1.如图1,AB∥CD, ∠1=45°, ∠D= ∠C,依次求出∠D, ∠C, ∠B的度数.
2.在下图所示的3个图中,a∥b,分别计算∠1的度数.DCAB1aaabbb11136°120°练一练!看看你会多少?如图:直线a、b被直线c、d所截,∠1=∠2, ∠4=110°求∠5的度数67∠BAD+∠D=180o如图,已知∵AB∥CD (已知)
∴∠1=∠2(两直线平行,内错角相等)
∠BAD+∠B=180o(两直线平行,同旁内角互补)
∠3=∠444、判断:下列推理过程对吗?若不对请改正。5、已知:如图, AB∥CD, CD∥EF, CH//DG
求证: ∠1=∠4 。 证明:
∵ AB∥CD ( )
∴ ∠1=∠2 ( )
∵ CD ∥ EF( )
∴∠3=∠4 ( )
∵ CH//DG ( )
∴∠2=∠3( )
∴∠1=∠4 ( )
已知已知两直线平行,同位角相等。两直线平行,内错角相等。等量代换已知两直线平行,内错角相等。(1)∵∠ADE=∠B=60o(已知)
∴DE∥BC(同位角相等,两直线平行)(2)∵DE∥BC(已证)
∴∠C=∠AED=40o(两直线平行,同位角相等) 6、如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么? 4、 如图,平行线AB、CD被直线AE所截,已知∠1=110o,则∠2、∠3、∠4分别是多少度?为什么?答: ∠ 2=110o,因为两直线平行,内错角相等, ∠ 2 = ∠ 1∠3= 110o,因为两直线平行,同位角相等, ∠3= ∠1∠4= 180o-110o=70o,因为两直线平行,同旁内角互补。归纳总结谈一谈:本节课你有何收获?
求证:AB∥CD。(一)(二)(三)训二问题2:根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢?内错角,同旁内角之间又有什么关系呢?
动手画一画! (1)用直尺和三角尺画出两条平行线 a∥b,再画一条截线c,使之与直线 a,b相交,并标出所形成的八个角.
(2)测量上面八个角的大小,记录下来.从中你能发现什么?性质1:两直线平行,同位角相等.平行线的性质:思考例如:如右图因为 a∥b,
所以 ∠1= ∠2(___________ ),
又 ∠3 = ___ (对顶角相等),
所以∠ 2 = ∠3.两直线平行,同位角相等。∠1练习:1、P22 练习
2、P26 6性质2:两直线平行,内错角相等。性质3:两直线平行,同旁内角互补。图形已知结果结论同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc平行线的判定小结a//b同位角相等
两直线平行a//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行平行线的性质你能区别平行线的判定与性质吗?判定性质平行线的判定是先知道角相等或互补,后知道两直线平行。平行线的性质是先知道两直线平行,后知道角相等或互补。平行线的判定与平行线 的性质的比较:平行线的判定与平行线的性质是因果互换的两类不同的定理,判定是说:满足了什么条件(性质)的两条直线是互相平行的性质是说:如果两条直线平行,就应该具有什么性质。例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯
形上底的一部分(如图)。要订造一块新的玻璃,已经
量得 ,你想一想,梯形另外两个角
各是多少度?解:因为梯形上.下底互相平行,所以
梯形的另外两个 角分别是ADBC1.如图1,AB∥CD, ∠1=45°, ∠D= ∠C,依次求出∠D, ∠C, ∠B的度数.
2.在下图所示的3个图中,a∥b,分别计算∠1的度数.DCAB1aaabbb11136°120°练一练!看看你会多少?如图:直线a、b被直线c、d所截,∠1=∠2, ∠4=110°求∠5的度数67∠BAD+∠D=180o如图,已知∵AB∥CD (已知)
∴∠1=∠2(两直线平行,内错角相等)
∠BAD+∠B=180o(两直线平行,同旁内角互补)
∠3=∠444、判断:下列推理过程对吗?若不对请改正。5、已知:如图, AB∥CD, CD∥EF, CH//DG
求证: ∠1=∠4 。 证明:
∵ AB∥CD ( )
∴ ∠1=∠2 ( )
∵ CD ∥ EF( )
∴∠3=∠4 ( )
∵ CH//DG ( )
∴∠2=∠3( )
∴∠1=∠4 ( )
已知已知两直线平行,同位角相等。两直线平行,内错角相等。等量代换已知两直线平行,内错角相等。(1)∵∠ADE=∠B=60o(已知)
∴DE∥BC(同位角相等,两直线平行)(2)∵DE∥BC(已证)
∴∠C=∠AED=40o(两直线平行,同位角相等) 6、如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么? 4、 如图,平行线AB、CD被直线AE所截,已知∠1=110o,则∠2、∠3、∠4分别是多少度?为什么?答: ∠ 2=110o,因为两直线平行,内错角相等, ∠ 2 = ∠ 1∠3= 110o,因为两直线平行,同位角相等, ∠3= ∠1∠4= 180o-110o=70o,因为两直线平行,同旁内角互补。归纳总结谈一谈:本节课你有何收获?
