6.3 实践与探索 第3课时 课件 (共24张PPT) 2023-2024学年数学华师版七年级下册
文档属性
| 名称 | 6.3 实践与探索 第3课时 课件 (共24张PPT) 2023-2024学年数学华师版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 20:56:47 | ||
图片预览








文档简介
(共24张PPT)
6.3 实践与探索
第3课时 工程问题及行程问题
学 习 目 标
1.通过分析具体问题中的工程关系,建立方程解决问题.(重点)
2.通过分析具体问题中的行程关系,建立方程解决问题.(重点)
3.进一步了解一元一次方程在解决实际问题中的应用,感受具体问题中数量之间的关系和变化规律(难点)
情 境 导 入
复
习
回
顾
1.做某件工作,甲单独做要8时才能完成,乙单独做要12时才能完成,问:
①甲做1时完成全部工作量的几分之几?___.
②乙做1时完成全部工作量的几分之几?___.
③甲、乙合做1时完成全部工作量的几分之几? .
④甲做x时完成全部工作量的几分之几? .
问题3
分析:设两人合作需x天完成.
效率之和
合作时间
工作总量
学校校办厂需制作一块广告牌,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
1
由题意,得方程
解得x=2.4
即两人合作要2.4天.
问题补充1:两人合作几天完成?
问题3
解:设两人合作需x天完成.
学校校办厂需制作一块广告牌,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
由题意,得方程
解得x=2
所以师傅和徒弟各分得225元.
问题补充2:现由徒弟先做1天,再两人合作,完成后共得报酬450元,如果按个人完成的工作量计算报酬,那么该如何分配?
所以
各部分工作量之和 = 工作总量
工程问题常见基本关系:
工作量=工作效率×工作时间
工作时间=
工作量
工作效率
基本等量关系:
工作效率=
工作量
工作时间
总结归纳
例 1
例 题 精 讲
将一批会计报表输入电脑,甲单独做需20h完成,乙单独做需12h完成,现在先由甲单独做4h,剩下的部分甲、乙合做完成,甲、乙两人合做的时间是多少?
效率 时间(小时) 工作量
甲
乙
1.如果利用表格解法,你能求出结果吗?
x+4
x
x=6
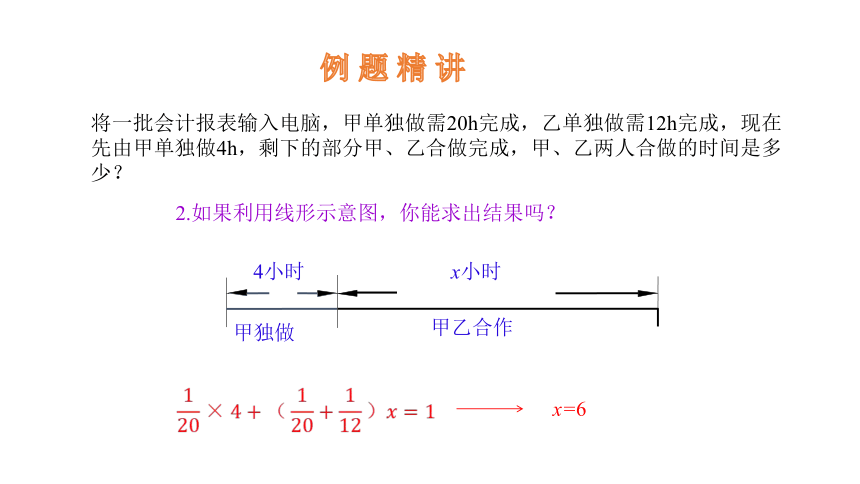
例 题 精 讲
将一批会计报表输入电脑,甲单独做需20h完成,乙单独做需12h完成,现在先由甲单独做4h,剩下的部分甲、乙合做完成,甲、乙两人合做的时间是多少?
2.如果利用线形示意图,你能求出结果吗?
x小时
4小时
甲独做
甲乙合作
x=6
随 堂 练 习
1.某人用三天做零件330个,已知第二天比第一天多做3个,第三天做的是第二天的2倍少3个,则他第一天做了多少个零件?
解:设他第一天做零件 x 个,则他第二天做零件 个, 第三天做零件________个,根据“某人用三天做零件330个”
列出方程得:__________________________.
解这个方程得:______________.
答:他第一天做零件 ________ 个.
x+3
2(x+3)-3
x+2x+3+(x+3)-3=330
x=81
81
2.一件工程,甲独做40天完成,乙独30天可以完成,丙独做24天可以完成,甲乙丙合做3天后,乙丙因事离开几天,乙离开的天数比丙多3天,结果前后共花费14天完成,问乙丙中途离开几天?
例 2
例 题 精 讲
分析:此问题是相遇问题,
等量关系为:汽车行程+摩托车行程=甲,乙两地之间路程。
240km
相遇地
甲
乙
汽车所行路程:36x km
甲乙两地相距240 km,汽车从甲地开往乙地,速度为36/km,摩托车从乙地开往甲地,速度是汽车的 .摩托车从乙地出发2小时30分钟后,汽车从甲地开往乙地,问汽车开出几小时后遇到摩托车?
摩托车先行的路程:
36× ×2.5 km
摩托车后来所行路程:
36× x km
解:设汽车开出x小时后遇到摩托车,
根据题意,得
36x+36×2/3·x+36×2/3×2.5=240,
解得x=2.
所以汽车开出2小时后遇到摩托车.
甲乙两地相距240 km,汽车从甲地开往乙地,速度为36/km,摩托车从乙地开往甲地,速度是汽车的 .摩托车从乙地出发2小时30分钟后,汽车从甲地开往乙地,问汽车开出几小时后遇到摩托车?
例 3
例 题 精 讲
若明明以每小时4千米的速度步行上学,哥哥半小时后发现明明忘了带作业,就骑车以每小时8千米追赶,问哥哥需要多长时间才可以送到作业?
此问题为追及问题,可通过画线段图理解题意、分析数量关系.
家
学 校
追 及 地
明明先走的路程:4×0.5
明明后走的路程:4x
哥哥所走的路程:8x
等量关系:
明明先走的路程
明明后走的路程
哥哥所走的路程
+
=
解:设哥哥要x小时才可以送到作业,
8x = 4x + 4×0.5.
解得 x = 0.5,
经检验符合题意.
答:哥哥要0.5小时才可以把作业送到.
行程问题常见基本关系:
总结归纳
1.基本题型
(1)同时出发(两段)
2.等量关系
(2)不同时出发 (三段 )
相遇问题
相遇问题:快行距+慢行距=原距
行程问题常见基本关系:
总结归纳
追及问题
1.基本题型:
(1)同时不同地出发
(2)不同时但同地出发
(3)不同时也不同地出发
2、等量关系:
(1)快者的路程=慢者的路程+原来的距离
(2)快者的路程=慢者先走的路程+慢着后走的路程
(3)快者的路程=慢者先走的路程+慢着后走的路程+原来的距离
追及问题:快行距-慢行距=原距
随 堂 练 习
1.甲、乙两车自西向东行驶,甲车的速度是每小时48千米,乙车的速度是每小时72千米,甲车开出25分钟后乙车开出,问几小时后乙车追上甲车?
答:乙开出 小时后追上甲车.
解:设乙车开出x小时后追上甲车,根据题意,得
×48+ 48x = 72x,
x= ,
解这个方 程,得
经检验,符合题意.
2.甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
15x+3×15x=180,
解得:x=3.
经检验符合题意,
答:经 3 小时两车相遇.
依题有:
解:设经x小时两人相遇.
当 堂 检 测
1.一项工程,甲单独做要10天完成,乙单独做要15天完成,甲单独做5天,然后甲、乙合作完成,共得到1000元,如果按照每人完成工作量计算报酬,那么甲、乙两人该如何分配?
解:设甲乙合作x天,由题意,得
(5+x) +x=1,
解得x=3.
甲分得1000×=800(元),
乙分得1000× =200(元).
所以甲乙分得800元,乙分得200元.
2.有一架飞机,最多能在空中飞行4小时,飞出时的速度是600千米/时,返回时的速度是550千米/时,这架飞机最多飞出多少千米就应返回?(精确到1千米)飞机本身的速度是多少?
解:设飞机最多飞出 x km.依题意,得
解得x=1 147.
经检验,符合题意.
答:飞机最多飞出 1 147千米.
3.甲、乙俩人在同一条路上前进,甲每小时行3km,乙每小时行5 km,甲于中午12时经过A地,乙于下午2点时经过A地,问乙下午几点能追上甲?
解:设经 x 小时乙追上甲,依题意,得
解得x=3.
经检验符合题意 .
答:乙下午5点能追上甲.
2×3+3x=5x,
则2+3=5 (小时),所以为下午5点.
4.甲、乙两人在400米长的环形跑道上跑步,甲分钟跑240米,乙每分钟
跑200米,二人同时同地同向出发,几分钟后二人相遇?若背向跑,几
分钟后相遇?
解:设x分钟后相遇,根据题意,得
(240-200)x=400,
解得x=10.
经检验,符合题意.
答:10分钟后相遇.
课 堂 小 结
实际问题
工程问题
行程问题
相遇问题
追及问题
行船问题
环形跑道问题
6.3 实践与探索
第3课时 工程问题及行程问题
学 习 目 标
1.通过分析具体问题中的工程关系,建立方程解决问题.(重点)
2.通过分析具体问题中的行程关系,建立方程解决问题.(重点)
3.进一步了解一元一次方程在解决实际问题中的应用,感受具体问题中数量之间的关系和变化规律(难点)
情 境 导 入
复
习
回
顾
1.做某件工作,甲单独做要8时才能完成,乙单独做要12时才能完成,问:
①甲做1时完成全部工作量的几分之几?___.
②乙做1时完成全部工作量的几分之几?___.
③甲、乙合做1时完成全部工作量的几分之几? .
④甲做x时完成全部工作量的几分之几? .
问题3
分析:设两人合作需x天完成.
效率之和
合作时间
工作总量
学校校办厂需制作一块广告牌,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
1
由题意,得方程
解得x=2.4
即两人合作要2.4天.
问题补充1:两人合作几天完成?
问题3
解:设两人合作需x天完成.
学校校办厂需制作一块广告牌,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
由题意,得方程
解得x=2
所以师傅和徒弟各分得225元.
问题补充2:现由徒弟先做1天,再两人合作,完成后共得报酬450元,如果按个人完成的工作量计算报酬,那么该如何分配?
所以
各部分工作量之和 = 工作总量
工程问题常见基本关系:
工作量=工作效率×工作时间
工作时间=
工作量
工作效率
基本等量关系:
工作效率=
工作量
工作时间
总结归纳
例 1
例 题 精 讲
将一批会计报表输入电脑,甲单独做需20h完成,乙单独做需12h完成,现在先由甲单独做4h,剩下的部分甲、乙合做完成,甲、乙两人合做的时间是多少?
效率 时间(小时) 工作量
甲
乙
1.如果利用表格解法,你能求出结果吗?
x+4
x
x=6
例 题 精 讲
将一批会计报表输入电脑,甲单独做需20h完成,乙单独做需12h完成,现在先由甲单独做4h,剩下的部分甲、乙合做完成,甲、乙两人合做的时间是多少?
2.如果利用线形示意图,你能求出结果吗?
x小时
4小时
甲独做
甲乙合作
x=6
随 堂 练 习
1.某人用三天做零件330个,已知第二天比第一天多做3个,第三天做的是第二天的2倍少3个,则他第一天做了多少个零件?
解:设他第一天做零件 x 个,则他第二天做零件 个, 第三天做零件________个,根据“某人用三天做零件330个”
列出方程得:__________________________.
解这个方程得:______________.
答:他第一天做零件 ________ 个.
x+3
2(x+3)-3
x+2x+3+(x+3)-3=330
x=81
81
2.一件工程,甲独做40天完成,乙独30天可以完成,丙独做24天可以完成,甲乙丙合做3天后,乙丙因事离开几天,乙离开的天数比丙多3天,结果前后共花费14天完成,问乙丙中途离开几天?
例 2
例 题 精 讲
分析:此问题是相遇问题,
等量关系为:汽车行程+摩托车行程=甲,乙两地之间路程。
240km
相遇地
甲
乙
汽车所行路程:36x km
甲乙两地相距240 km,汽车从甲地开往乙地,速度为36/km,摩托车从乙地开往甲地,速度是汽车的 .摩托车从乙地出发2小时30分钟后,汽车从甲地开往乙地,问汽车开出几小时后遇到摩托车?
摩托车先行的路程:
36× ×2.5 km
摩托车后来所行路程:
36× x km
解:设汽车开出x小时后遇到摩托车,
根据题意,得
36x+36×2/3·x+36×2/3×2.5=240,
解得x=2.
所以汽车开出2小时后遇到摩托车.
甲乙两地相距240 km,汽车从甲地开往乙地,速度为36/km,摩托车从乙地开往甲地,速度是汽车的 .摩托车从乙地出发2小时30分钟后,汽车从甲地开往乙地,问汽车开出几小时后遇到摩托车?
例 3
例 题 精 讲
若明明以每小时4千米的速度步行上学,哥哥半小时后发现明明忘了带作业,就骑车以每小时8千米追赶,问哥哥需要多长时间才可以送到作业?
此问题为追及问题,可通过画线段图理解题意、分析数量关系.
家
学 校
追 及 地
明明先走的路程:4×0.5
明明后走的路程:4x
哥哥所走的路程:8x
等量关系:
明明先走的路程
明明后走的路程
哥哥所走的路程
+
=
解:设哥哥要x小时才可以送到作业,
8x = 4x + 4×0.5.
解得 x = 0.5,
经检验符合题意.
答:哥哥要0.5小时才可以把作业送到.
行程问题常见基本关系:
总结归纳
1.基本题型
(1)同时出发(两段)
2.等量关系
(2)不同时出发 (三段 )
相遇问题
相遇问题:快行距+慢行距=原距
行程问题常见基本关系:
总结归纳
追及问题
1.基本题型:
(1)同时不同地出发
(2)不同时但同地出发
(3)不同时也不同地出发
2、等量关系:
(1)快者的路程=慢者的路程+原来的距离
(2)快者的路程=慢者先走的路程+慢着后走的路程
(3)快者的路程=慢者先走的路程+慢着后走的路程+原来的距离
追及问题:快行距-慢行距=原距
随 堂 练 习
1.甲、乙两车自西向东行驶,甲车的速度是每小时48千米,乙车的速度是每小时72千米,甲车开出25分钟后乙车开出,问几小时后乙车追上甲车?
答:乙开出 小时后追上甲车.
解:设乙车开出x小时后追上甲车,根据题意,得
×48+ 48x = 72x,
x= ,
解这个方 程,得
经检验,符合题意.
2.甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
15x+3×15x=180,
解得:x=3.
经检验符合题意,
答:经 3 小时两车相遇.
依题有:
解:设经x小时两人相遇.
当 堂 检 测
1.一项工程,甲单独做要10天完成,乙单独做要15天完成,甲单独做5天,然后甲、乙合作完成,共得到1000元,如果按照每人完成工作量计算报酬,那么甲、乙两人该如何分配?
解:设甲乙合作x天,由题意,得
(5+x) +x=1,
解得x=3.
甲分得1000×=800(元),
乙分得1000× =200(元).
所以甲乙分得800元,乙分得200元.
2.有一架飞机,最多能在空中飞行4小时,飞出时的速度是600千米/时,返回时的速度是550千米/时,这架飞机最多飞出多少千米就应返回?(精确到1千米)飞机本身的速度是多少?
解:设飞机最多飞出 x km.依题意,得
解得x=1 147.
经检验,符合题意.
答:飞机最多飞出 1 147千米.
3.甲、乙俩人在同一条路上前进,甲每小时行3km,乙每小时行5 km,甲于中午12时经过A地,乙于下午2点时经过A地,问乙下午几点能追上甲?
解:设经 x 小时乙追上甲,依题意,得
解得x=3.
经检验符合题意 .
答:乙下午5点能追上甲.
2×3+3x=5x,
则2+3=5 (小时),所以为下午5点.
4.甲、乙两人在400米长的环形跑道上跑步,甲分钟跑240米,乙每分钟
跑200米,二人同时同地同向出发,几分钟后二人相遇?若背向跑,几
分钟后相遇?
解:设x分钟后相遇,根据题意,得
(240-200)x=400,
解得x=10.
经检验,符合题意.
答:10分钟后相遇.
课 堂 小 结
实际问题
工程问题
行程问题
相遇问题
追及问题
行船问题
环形跑道问题
