7.3 三元一次方程组及其解法 课件 (共18张PPT) 2023-2024学年数学华师版七年级下册
文档属性
| 名称 | 7.3 三元一次方程组及其解法 课件 (共18张PPT) 2023-2024学年数学华师版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 285.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 21:02:06 | ||
图片预览





文档简介
(共18张PPT)
7.3 三元一次方程组及其解法
学 习 目 标
1.了解三元一次方程组的概念,会解简单的三元一次方程组.(重点)
2.针对方程组的特点,选择最合适最简便的解法.(难点)
情 境 导 入
复
习
回
顾
问题1:什么叫二元一次方程组?
把两个二元一次方程合在一起,就组成了二元一次方程组.
二元一次方程组
消元
一元一次方程
代入消元法和加减消元法
消元法
问题2:解二元一次方程组的基本思路是什么?
问题3:解二元一次方程组有哪几种方法?
在7.1节中,我们应用二元一次方程组,求出了勇士队在“我们的小世界杯”足球赛第一轮比赛中胜与平的场数.
在第二轮比赛中,勇士队参加了10场比赛,按同样的记分规则,共得18分.已知勇士队在比赛中胜的场数正好等于平与负的场数之和,那么勇士队在第二轮比赛中胜、平、负的场数各是多少?
问题
思考:这个问题可以用哪些方法求解
算术方法
列出一元一次方程
列二元一次方程组
试一试,并对不同的方法进行比较?
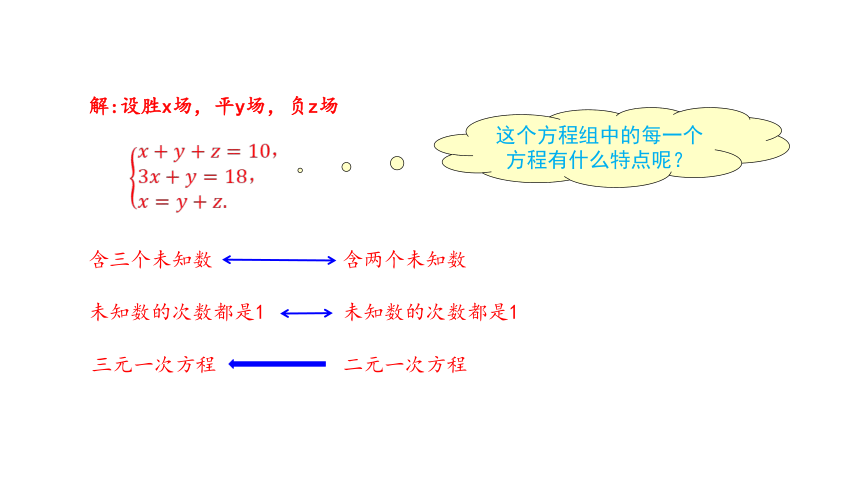
问题中有三个未知数,如果设这个队在第二轮比赛中胜、平、负的场数分别为x、y、z,又将怎样呢?
分析:审题,可得数量关系.
胜的场数+平的场数+负的场数=10
胜的得分+平的得分+负的得分=18
胜的场数=平的场数+负的场数
二元一次方程
三元一次方程
含两个未知数
未知数的次数都是1
含三个未知数
未知数的次数都是1
解:设胜x场,平y场,负z场
这个方程组中的每一个方程有什么特点呢?
知 识 讲 解
知识点 三元一次方程组
含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
思考
怎样解三元一次方程组呢?
回忆一下二元一次方程组的解法,从中能得到什么启示?
①
②
③
分析:方程③中,x是用含y和z的代数式来表示的,将它分别代入方程①、②,得到
解这个关于y、z的二元一次方程组,得
将y=3,z=2代入方程组,得x=5.
所以这个三元一次方程组的解是
试一试
下面的三元一次方程组能否应用加减消元法求解?或者能否利用方程③,直接消去方程①中的y+z?比较一下,哪种方法更简便?
①
②
③
解:3×①-②,得2y+3z=12. ④
①-③,得2y+2z=10. ⑤
④-⑤,得z=2.
将z=2代入①、③,得
解得
所以
解:由③,得y+z=x. ④
将④代入①,得2x=10,即x=5.
将x=5代入②,得15+y=18,
即y=3.
将x=5、y=3代入③,得5=3+z,
即z=2.
所以
例 题 精 讲
例 1
解方程组:
解:由方程②,得z=7-3x+2y. ④
代入④,得z=7-3-6=-2.
所以原方程组的解是
将④分别代入方程①和③,得
整理,得
解这个二元一次方程组,得
概括
这里,我们用的是代入消元法:先由方程②,用含x、y的代数式表示z,再分别代入方程①和③,消去未知数z,转化为只含有x、y的二元一次方程组求解.
能否先消去x(或y)?怎么做?比较一下,哪个更简便?
例 题 精 讲
例 2
解方程组:
解:③-②,得3x+6z=-24,即x+2z=-8.
所以原方程组的解是
得方程组
解得
①×3+②×4,得17x-17z=17,即x-z=1.
将x=-2,z=-3代入方程②,得y=0.
通过“加减”,先消去y,得到关于x、z的二元一次方程,然后解方程组!
能否先消去z(或x)?怎么做?比较一下,哪个更简便?
概括
上述例1和例2的解答分别应用了代入消元法和加减消元法,先消去某一个未知数,将三元一次方程组转化为二元一次方程组,然后解所得的二元一次方程组,得到两个未知数的值,进而求出第三个未知数的值,从而得到原方程组的解.
注意
(1)三个方程中若有一个未知项的系数是1或-1时,可以考虑用代入消元法.
(2)如果三元一次方程组中有一个方程是二元一次方程,则可以先通过对另外两个方程进行消元,消去缺少的那个元.缺某元,消某元.
(3)若三个方程均为三元一次方程,一般选取系数较小或成倍数的未知数消元,两次消元必须是消同一个未知数.
1.下列方程组不是三元一次方程组的是( )
D
A
随 堂 练 习
2.三元一次方程组 的解是( )
A.
B.
C.
D.
B.
C.
D.
A.
1.运用加减消元法解方程组 较简单的方法是( )
A.①+②,②×2+③ 消去未知数z
B.①-②,②×2+3 消去未知数z
C.①×2+②×3,②×3+③×2 消去未知数y
D.①×2+②×3,②×3-③×2消去未知数y
A
2.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
D
当 堂 检 测
3.解下列方程组:
(1)
解:由②,得y=5z-11. ④
所以原方程组的解是
由③和⑤,解得
把④代入①,得3x-2(5z-11)=5,
即3x-10z=-17. ⑤
将z=2代入方程④,得y=-1.
所以原方程组的解是
(2)
解:①+②,得4x+3z=18. ④
由④和⑤,解得
②-③,得2x+5z=16. ⑤
将x=3,z=2代入①,得y=1.
1.三元一次方程组的定义:
只含有三个未知数,并且含有未知数项的次数都是1的整式方程组叫做三元一次方程组.
2.解三元一次方程组的基本思想:
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
代入法加减法
代入法加减法
课 堂 小 结
7.3 三元一次方程组及其解法
学 习 目 标
1.了解三元一次方程组的概念,会解简单的三元一次方程组.(重点)
2.针对方程组的特点,选择最合适最简便的解法.(难点)
情 境 导 入
复
习
回
顾
问题1:什么叫二元一次方程组?
把两个二元一次方程合在一起,就组成了二元一次方程组.
二元一次方程组
消元
一元一次方程
代入消元法和加减消元法
消元法
问题2:解二元一次方程组的基本思路是什么?
问题3:解二元一次方程组有哪几种方法?
在7.1节中,我们应用二元一次方程组,求出了勇士队在“我们的小世界杯”足球赛第一轮比赛中胜与平的场数.
在第二轮比赛中,勇士队参加了10场比赛,按同样的记分规则,共得18分.已知勇士队在比赛中胜的场数正好等于平与负的场数之和,那么勇士队在第二轮比赛中胜、平、负的场数各是多少?
问题
思考:这个问题可以用哪些方法求解
算术方法
列出一元一次方程
列二元一次方程组
试一试,并对不同的方法进行比较?
问题中有三个未知数,如果设这个队在第二轮比赛中胜、平、负的场数分别为x、y、z,又将怎样呢?
分析:审题,可得数量关系.
胜的场数+平的场数+负的场数=10
胜的得分+平的得分+负的得分=18
胜的场数=平的场数+负的场数
二元一次方程
三元一次方程
含两个未知数
未知数的次数都是1
含三个未知数
未知数的次数都是1
解:设胜x场,平y场,负z场
这个方程组中的每一个方程有什么特点呢?
知 识 讲 解
知识点 三元一次方程组
含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
思考
怎样解三元一次方程组呢?
回忆一下二元一次方程组的解法,从中能得到什么启示?
①
②
③
分析:方程③中,x是用含y和z的代数式来表示的,将它分别代入方程①、②,得到
解这个关于y、z的二元一次方程组,得
将y=3,z=2代入方程组,得x=5.
所以这个三元一次方程组的解是
试一试
下面的三元一次方程组能否应用加减消元法求解?或者能否利用方程③,直接消去方程①中的y+z?比较一下,哪种方法更简便?
①
②
③
解:3×①-②,得2y+3z=12. ④
①-③,得2y+2z=10. ⑤
④-⑤,得z=2.
将z=2代入①、③,得
解得
所以
解:由③,得y+z=x. ④
将④代入①,得2x=10,即x=5.
将x=5代入②,得15+y=18,
即y=3.
将x=5、y=3代入③,得5=3+z,
即z=2.
所以
例 题 精 讲
例 1
解方程组:
解:由方程②,得z=7-3x+2y. ④
代入④,得z=7-3-6=-2.
所以原方程组的解是
将④分别代入方程①和③,得
整理,得
解这个二元一次方程组,得
概括
这里,我们用的是代入消元法:先由方程②,用含x、y的代数式表示z,再分别代入方程①和③,消去未知数z,转化为只含有x、y的二元一次方程组求解.
能否先消去x(或y)?怎么做?比较一下,哪个更简便?
例 题 精 讲
例 2
解方程组:
解:③-②,得3x+6z=-24,即x+2z=-8.
所以原方程组的解是
得方程组
解得
①×3+②×4,得17x-17z=17,即x-z=1.
将x=-2,z=-3代入方程②,得y=0.
通过“加减”,先消去y,得到关于x、z的二元一次方程,然后解方程组!
能否先消去z(或x)?怎么做?比较一下,哪个更简便?
概括
上述例1和例2的解答分别应用了代入消元法和加减消元法,先消去某一个未知数,将三元一次方程组转化为二元一次方程组,然后解所得的二元一次方程组,得到两个未知数的值,进而求出第三个未知数的值,从而得到原方程组的解.
注意
(1)三个方程中若有一个未知项的系数是1或-1时,可以考虑用代入消元法.
(2)如果三元一次方程组中有一个方程是二元一次方程,则可以先通过对另外两个方程进行消元,消去缺少的那个元.缺某元,消某元.
(3)若三个方程均为三元一次方程,一般选取系数较小或成倍数的未知数消元,两次消元必须是消同一个未知数.
1.下列方程组不是三元一次方程组的是( )
D
A
随 堂 练 习
2.三元一次方程组 的解是( )
A.
B.
C.
D.
B.
C.
D.
A.
1.运用加减消元法解方程组 较简单的方法是( )
A.①+②,②×2+③ 消去未知数z
B.①-②,②×2+3 消去未知数z
C.①×2+②×3,②×3+③×2 消去未知数y
D.①×2+②×3,②×3-③×2消去未知数y
A
2.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
D
当 堂 检 测
3.解下列方程组:
(1)
解:由②,得y=5z-11. ④
所以原方程组的解是
由③和⑤,解得
把④代入①,得3x-2(5z-11)=5,
即3x-10z=-17. ⑤
将z=2代入方程④,得y=-1.
所以原方程组的解是
(2)
解:①+②,得4x+3z=18. ④
由④和⑤,解得
②-③,得2x+5z=16. ⑤
将x=3,z=2代入①,得y=1.
1.三元一次方程组的定义:
只含有三个未知数,并且含有未知数项的次数都是1的整式方程组叫做三元一次方程组.
2.解三元一次方程组的基本思想:
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
代入法加减法
代入法加减法
课 堂 小 结
