平行线的性质及平移例题精析及练习(含答案)2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 平行线的性质及平移例题精析及练习(含答案)2023-2024学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 19:51:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
平行线的性质及平移例题精析及练习
思维导图
重 难点分析
重点分析:
1.平行线的性质:(1)两直线平行,同位角相等.(2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.
2.利用命题的定义来判断语句是否为命题,关键看是否为一个判断句.命题由题设和结论两部分组成,可以写成“如果……,那么……”的形式,其中“如果”后写题设,“那么”后写结论.
3.经过推理证实的真命题叫做定理,定理可以作为继续推理的依据.
4.证明一个命题是真命题,主要依据已知的定理、公理或相关数学性质;而判断一个命题是假命题,只要举一个反例即可.
5.平移的概念:一个图形沿着某个方向运动,在移动过程中,原图形上的每一个点都沿着同一个方向移动相等的距离,这样的图形运动叫做图形的平移.
6.平移的性质:平移不改变图形的形状和大小.一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
难点分析:
1.注意平行的性质与判定的区别与联系:区别是条件与结论不同,联系是条件与结论互换位置;性质是由平行线得到角的关系,判定是由角的关系得到平行线.
2.连接平移前后两个图形的对应点的线段平行(或在同一条直线上)且相等,注意一定要对应点相连,连线的平行是指它们的位置关系,相等是指它们的数量关系.
例题精析
例1 如图,把边长为2的正方形的局部进行图1~图4的变换,拼成图5,则图5的面积是( ).
A.18 B.16 C.12 D.8
思路点拨 根据平移的基本性质,平移不改变图形的形状和大小,即图形平移后面积不变,则图5的面积可求.
解题过程 一个正方形的面积为4,而把一个正方形从图1~图4进行变换,面积并没有改变,图5由4个图4构成,故图5的面积为4×4=16.
故选B.
方法归纳 本题考查图形拼接与平移的变换,解决本题的关键是要知道平移不改变图形的形状和大小,即面积没有改变.
易错误区 图5由4个图4构成,没有多也没有少,本题易误认为图5有残缺.
例2 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题,甲同学认为该命题是真命题,并作图如图1所示,已知AB∥DE,BC∥DF,BC与DE交于点 G.
(1)根据甲同学的作图及题设,求证:
(2)乙同学对甲同学的判断提出质疑,认为该命题不一定成立,是假命题,并作图如图2所示,题设与甲同学相同,得到∠B≠∠D.根据乙同学的作图,试判断∠B与∠D的数量关系,并说明理由.
(3)请你根据以上内容,总结出一个真命题.
思路点拨 (1)根据平行线的性质得 那么∠B=∠D.(2)根据平行线的性质得. ∠DGB,那么∠B+∠D=180°.(3)综合(1)(2)的结论可知,两边分别平行的两个角相等或互补.
解题过程 (1)∵AB∥DE,BC∥DF,
∴∠B=∠CGE,∠D=∠CGE(两直线平行,同位角相等).
∴∠B=∠D(等量代换).
(2)∠B+∠D=180°.理由如下:
∵AB∥DE,BC∥DF,
∴∠B+∠DGB=180°(两直线平行,同旁内角互补),
∠D=∠DGB(两直线平行,内错角相等).
∴∠B+∠D=180°(等量代换).
(3)两边分别平行的两个角相等或互补.
方法归纳 本题考查了命题的真假、推理论证及平行线的相关知识,熟练掌握平行线的性质是解题的关键.
易错误区 要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.推理证明的过程中需要全面考虑各种情况,才能得出正确结论.
例3 如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,P是BC上的一点.
(1)求∠EFC与∠E的度数.
(2)若∠BFP=46°,请判断CE与PF是否平行 并说明理由.
思路点拨 (1)由. 可得出AB∥CD,根据平行线的性质可得出∠1=∠DFE,再结合∠1=3∠2,∠2=24°,通过角的计算即可得出∠EFC与∠E的度数.(2)由(1)中∠E的度数结合. 即可得出∠E≠∠BFP,从而得出CE与PF不平行.
解题过程 (1)∵∠A+∠D=180°,∴AB∥CD.∴∠1=∠DFE.
∵∠1=3∠2,∠2=24°,∴∠1=∠DFE=72°.
(2)不平行.理由如下:
∵∠E=48°,∠BFP=46°,∴∠E≠∠BFP.
∴CE与PF不平行.
方法归纳 本题考查平行线的判定与性质,解题的关键是:(1)得出AB∥CD.(2)熟悉平行线的判定定理.解决该类型题目时,根据相等(或互补)的角证出两直线平行是关键.
易错误区 判定两条直线平行,需要根据角的关系来判断,不能只凭观察得出结果.
例4 珠江流域某江段江水流向经过B,C,D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,求∠CDE的度数.
思路点拨 由已知可得AB∥DE,过点C作CF∥AB,由平行线的性质可得∠BCF+∠ABC=180°,所以能求出∠BCF,继而求出. 又由平行线的传递性得CF∥DE,所以∠CDE=∠DCF.
解题过程 如图,过点C作CF∥AB.∴∠BCF+∠ABC=180°.
∵∠ABC=120°,∴∠BCF=60°.
又∵∠BCD=80°,∴∠DCF=∠BCD-∠BCF=20°.
∵江水流向经过B,C,D三点拐弯后与原来相同,
∴AB∥DE.∴CF∥DE.∴∠CDE=∠DCF=20°.
方法归纳 本题考查的知识点是平行线的性质,关键是过点C先作AB的平行线,由平行线的性质求解.
易错误区 作辅助线只能作其中一条直线的平行线,然后利用传递性说明三条直线平行,不能出现过点C作CF∥AB∥DE的错误.
例5 如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD.
(2)若∠B=100°,点E,F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图2,求∠FAC的度数.
(3)若点 E 在直线 CD上,且满足 求∠ACD:∠AED的值(用含n的代数式表示).(请自己画出正确的图形,并解答)
思路点拨 (1)依据平行线的性质以及判定,即可得到AB∥CD.
(2)依据AC平分∠BAE,AF平分∠DAE,即可得到 进而得出 (3)分两种情况讨论:当点E在线段CD上时;当点E在DC的延长线上时,分别依据AB∥CD,得到 的值.
解题过程 (1)∵AD∥BC,∴∠A+∠B=180°.
又∵∠B=∠D,∴∠D+∠A=180°.∴AB∥CD.
∵AC平分∠BAE,AF平分∠DAE,
(3)分两种情况:
当点E在线段CD上时,如图3.
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又
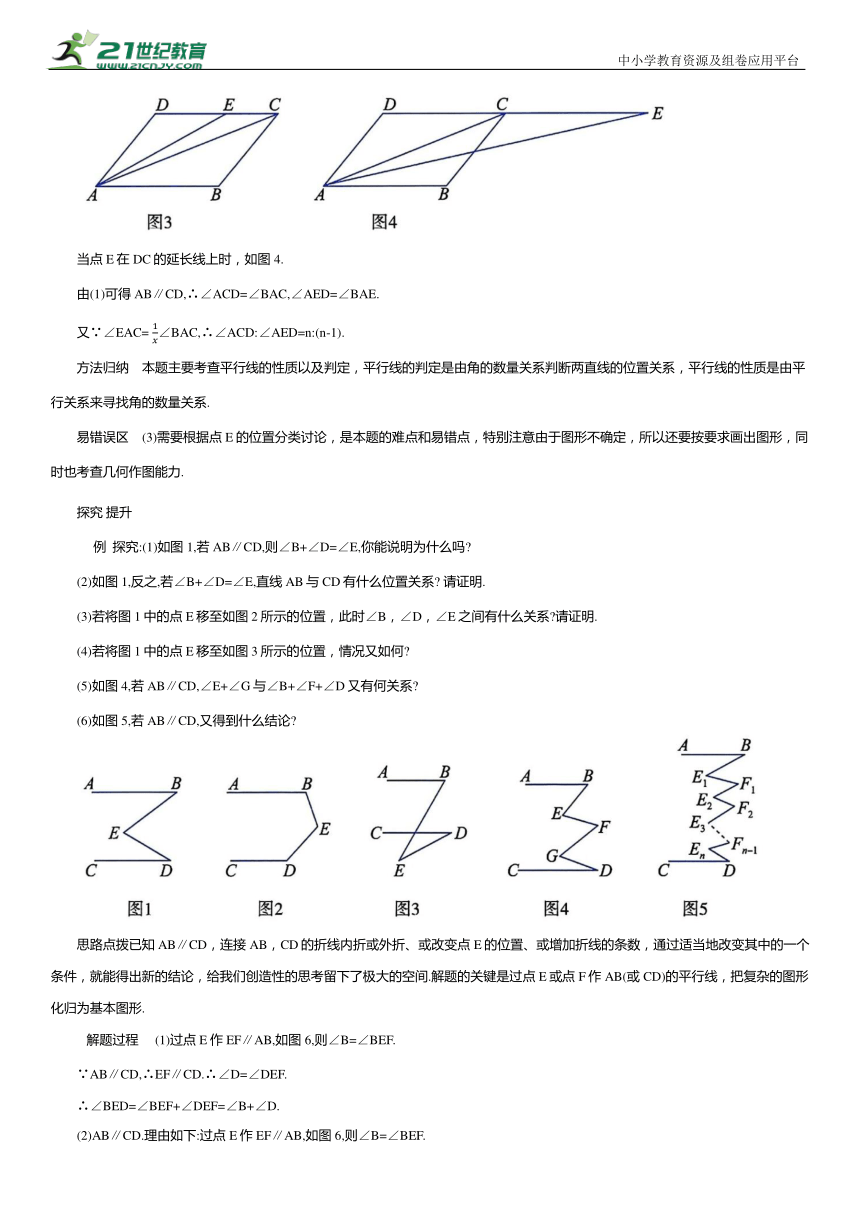
当点E在DC的延长线上时,如图4.
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又∵∠EAC= ∠BAC,∴∠ACD:∠AED=n:(n-1).
方法归纳 本题主要考查平行线的性质以及判定,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
易错误区 (3)需要根据点E的位置分类讨论,是本题的难点和易错点,特别注意由于图形不确定,所以还要按要求画出图形,同时也考查几何作图能力.
探究 提升
例 探究:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗
(2)如图1,反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系 请证明.
(3)若将图1中的点E移至如图2所示的位置,此时∠B,∠D,∠E之间有什么关系 请证明.
(4)若将图1中的点E移至如图3所示的位置,情况又如何
(5)如图4,若AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系
(6)如图5,若AB∥CD,又得到什么结论
思路点拨已知AB∥CD,连接AB,CD的折线内折或外折、或改变点E的位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间.解题的关键是过点E或点F作AB(或CD)的平行线,把复杂的图形化归为基本图形.
解题过程 (1)过点E作EF∥AB,如图6,则∠B=∠BEF.
∵AB∥CD,∴EF∥CD.∴∠D=∠DEF.
∴∠BED=∠BEF+∠DEF=∠B+∠D.
(2)AB∥CD.理由如下:过点E作EF∥AB,如图6,则∠B=∠BEF.
∵∠BED=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF.∴EF∥CD.∴AB∥CD.
(3)∠BED+∠B+∠D=360°.理由如下:
若将点E移至如图2所示位置,过点E作EF∥AB,如图7.
∵AB∥CD,∴EF∥CD.
∴∠D+∠DEF=180°,∠B+∠BEF=180°.∴∠BED+∠B+∠D=360°.
(4)如图8,∵AB∥CD,∴∠B=∠BFD.
∵∠D+∠E+∠EFD=180°,∠BFD+∠EFD=180°,
∴∠D+∠E=∠BFD.∴∠D+∠E=∠B.
(5)如图9,过点F作. ,则由(1)的结论可知.
又∵∠EFG=∠EFH+∠HFG,∴∠E+∠G=∠B+∠EFG+∠D.
(6)由以上可知. .
方法归纳 本题考查了平行线的性质与判定,关键是添加适当的辅助线,把复杂的图形化归为基本图形,使问题得以简化.
易错误区 为了合理应用平行线的性质定理,过折点作平行线时画射线比较好,但要注意射线的方向,尽量避免添加辅助线后的图形复杂化.
专项训 练
拓展训练
A组
1.如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( ).
A.36° B.72°
C. 108° D. 118°
2.如图,三角形DEF经过怎样的平移可得三角形ABC( ).
A.先向左平移4个单位,再向下平移2个单位
B.先向右平移4个单位,再向下平移2个单位
C.先向右平移4个单位,再向上平移2个单位
D.先向左平移4个单位,再向上平移2个单位
3.【济南】如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( ).
A.20° B.35° C.55° D.70°
4.如图,. ,则∠4的度数为 .
5.将一副三角尺按如图所示摆放,边DE∥AB,则∠1= .
6.将一张长方形纸片折叠成如图的图形,若∠ABC=26°,则∠
7.如图,图1为北斗七星的位置图,图2将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=105°,则∠B-∠CGF= .
8.在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°(已知),
∴∠B=∠DCE( ).
又∵∠B=∠D( ),
∴∠DCE=∠D( ).
∴AD∥BE( ).
∴∠E=∠DFE( ).
9.潜望镜中的两面镜子MN和PQ是互相平行的,如图,光线AB经镜面反射后, 射入的光线AB与射出的光线CD平行吗 为什么
10.如图,已知AE⊥BC,FG⊥BC,∠1=∠2.
(1)求证:AE∥FG.
(2)求证:AB∥CD.
(3)若∠D=∠3+50°,∠CBD=80°,求∠C的度数.
B 组
11.如图,有两条长分别为a,b的铁丝,其中长为a的铁丝恰好围成一个大正方形;AB是大正方形的对角线,把AB分成n条相等的线段,再以每条线段作为小正方形的对角线,长为b的铁丝恰好能围成n个这样的小正方形.若均不考虑接口情况,则a,b的大小关系是( ).
A. a>b B. a12.【莱芜】如图,AB∥CD,∠BED=61°,∠ABE的平分线与∠CDE的平分线交于点F,则∠DFB等于( ).
A.149° B.149.5° C.150°
13.下列命题:①在同一平面内,过一点有且只有一条直线与已知直线垂直;②过一点有且只有一条直线与已知直线平行;③若b∥c,a∥c,则b∥a;④若∠1=40°,∠2的两边与∠1的两边分别平行,则∠2=40°或140°;⑤若b⊥c,a⊥c,则b∥a.其中是真命题的有 .(填序号)
14.如图,已知. CE平分 则 的度数为 .
15.如图, .求证:
16.如图,已知AB∥CD,点C在点D的右侧,BE平分. ,DE平分 BE,DE所在的直线交于点E,.
(1)求 的度数.
(2)若 ,求∠BED的度数(用含n的代数式表示).
(3)将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若 求∠BED的度数(用含n的代数式表示).
走进重高
1.【鞍山】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( ).
A.50° B.55° C.60° D.65°
2.【襄阳】如图,直线BC∥AE,CD⊥AB于点D,若∠BCD=40°,则∠1的度数是( ).
A.60° B.50° C.40° D.30°
3.【通辽】如图,∠AOB的一边OA为平面镜,∠AOB=37°45',在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
4.将一两边互相平行的纸带沿EF折叠,如图1, ,设∠AED'=x°.
(1)∠EFB= (用含x的代数式表示).
(2)若将图1继续沿BF折叠成图2,则. (用含x的代数式表示).
5.【武汉】如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
高分夺冠
1.如图,a∥b,设 下列说法中,正确的是( ).
A.若∠2=∠3,则.
B.若∠1=∠4,则.
C.若∠1=2∠2=2∠3,则.
D.若∠1=∠2=∠3,则.
2.如图,已知直线AB,CD被直线AC所截, E是平面内任意一点(点E不在直线AB,CD,AC上),设 β.下列各式:①α+β;②α-β;③β-α;④α/ -β;⑤360°-α-β.其中可以表示∠AEC度数的是 (填序号).
3.如图是某公园里一处长方形风景欣赏区ABCD,长AB=50m,宽BC=25m.为方便游人观赏,公园特意修建了如图所示的小路(图中非涂色部分),小路的宽均为1m,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为 m.
4.已知E,F分别是AB,CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD.
(2)如图2,若∠P=∠PFD-∠BEP,求证:AB∥CD.
(3)如图3,AB∥CD,移动点E,F使∠EPF=90°,作∠PEG=∠BEP,求 的值.
拓展训练
A组
1. C 2. A 3. B 4.78°5.105° 6.128°
7.115° 8.同旁内角互补,两直线平行 两直线平行,同位角相等 已知 等量代换 内错角相等,两直线平行 两直线平行,内错角相等
9.射入的光线AB与射出的光线CD平行.理由如下:∵MN∥PQ,
∴∠2=∠3(两直线平行,内错角相等).
又∵∠1=∠2,∠3=∠4,∴∠1+∠2=∠3+∠4.
,即∠5=∠6.
∴AB∥CD(内错角相等,两直线平行).
10.(1)∵AE⊥BC,FG⊥BC,∴AE∥FG.
(2)∵AE∥FG,∴∠1=∠CFG.
∵∠1=∠2,∴∠CFG=∠2.∴AB∥CD.
(3)∵AB∥CD,∴∠D+∠ABD=180°.
∴∠D+∠3+∠CBD=180°.
∵AB∥CD,∴∠C=∠3=25°.
B组
11. C 12. B 13.①③④ 14.100°
15.∵∠BAP+∠APD=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行).
∴∠BAP=∠APC(两直线平行,内错角相等).
又∵∠1=∠2(已知),∴∠FPA=∠EAP.
∴AE∥PF(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
16.(1)∵DE平分∠ADC,∠ADC=70°,
(2)∵BE平分∠ABC,
∵AB∥CD,∴∠BCD=∠ABC=n°.
∵∠CBE+∠BED=∠EDC+∠BCD,即
(3)如图,∵BE平分∠ABC,DE平分∠ADC,
∵AB∥CD,∴∠BAD+∠ADC=180°.
在四边形ADEB中,
走进重高
1. D 2. B 3.75°30′(或75.5°)
平行线的性质及平移例题精析及练习
思维导图
重 难点分析
重点分析:
1.平行线的性质:(1)两直线平行,同位角相等.(2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.
2.利用命题的定义来判断语句是否为命题,关键看是否为一个判断句.命题由题设和结论两部分组成,可以写成“如果……,那么……”的形式,其中“如果”后写题设,“那么”后写结论.
3.经过推理证实的真命题叫做定理,定理可以作为继续推理的依据.
4.证明一个命题是真命题,主要依据已知的定理、公理或相关数学性质;而判断一个命题是假命题,只要举一个反例即可.
5.平移的概念:一个图形沿着某个方向运动,在移动过程中,原图形上的每一个点都沿着同一个方向移动相等的距离,这样的图形运动叫做图形的平移.
6.平移的性质:平移不改变图形的形状和大小.一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
难点分析:
1.注意平行的性质与判定的区别与联系:区别是条件与结论不同,联系是条件与结论互换位置;性质是由平行线得到角的关系,判定是由角的关系得到平行线.
2.连接平移前后两个图形的对应点的线段平行(或在同一条直线上)且相等,注意一定要对应点相连,连线的平行是指它们的位置关系,相等是指它们的数量关系.
例题精析
例1 如图,把边长为2的正方形的局部进行图1~图4的变换,拼成图5,则图5的面积是( ).
A.18 B.16 C.12 D.8
思路点拨 根据平移的基本性质,平移不改变图形的形状和大小,即图形平移后面积不变,则图5的面积可求.
解题过程 一个正方形的面积为4,而把一个正方形从图1~图4进行变换,面积并没有改变,图5由4个图4构成,故图5的面积为4×4=16.
故选B.
方法归纳 本题考查图形拼接与平移的变换,解决本题的关键是要知道平移不改变图形的形状和大小,即面积没有改变.
易错误区 图5由4个图4构成,没有多也没有少,本题易误认为图5有残缺.
例2 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题,甲同学认为该命题是真命题,并作图如图1所示,已知AB∥DE,BC∥DF,BC与DE交于点 G.
(1)根据甲同学的作图及题设,求证:
(2)乙同学对甲同学的判断提出质疑,认为该命题不一定成立,是假命题,并作图如图2所示,题设与甲同学相同,得到∠B≠∠D.根据乙同学的作图,试判断∠B与∠D的数量关系,并说明理由.
(3)请你根据以上内容,总结出一个真命题.
思路点拨 (1)根据平行线的性质得 那么∠B=∠D.(2)根据平行线的性质得. ∠DGB,那么∠B+∠D=180°.(3)综合(1)(2)的结论可知,两边分别平行的两个角相等或互补.
解题过程 (1)∵AB∥DE,BC∥DF,
∴∠B=∠CGE,∠D=∠CGE(两直线平行,同位角相等).
∴∠B=∠D(等量代换).
(2)∠B+∠D=180°.理由如下:
∵AB∥DE,BC∥DF,
∴∠B+∠DGB=180°(两直线平行,同旁内角互补),
∠D=∠DGB(两直线平行,内错角相等).
∴∠B+∠D=180°(等量代换).
(3)两边分别平行的两个角相等或互补.
方法归纳 本题考查了命题的真假、推理论证及平行线的相关知识,熟练掌握平行线的性质是解题的关键.
易错误区 要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.推理证明的过程中需要全面考虑各种情况,才能得出正确结论.
例3 如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,P是BC上的一点.
(1)求∠EFC与∠E的度数.
(2)若∠BFP=46°,请判断CE与PF是否平行 并说明理由.
思路点拨 (1)由. 可得出AB∥CD,根据平行线的性质可得出∠1=∠DFE,再结合∠1=3∠2,∠2=24°,通过角的计算即可得出∠EFC与∠E的度数.(2)由(1)中∠E的度数结合. 即可得出∠E≠∠BFP,从而得出CE与PF不平行.
解题过程 (1)∵∠A+∠D=180°,∴AB∥CD.∴∠1=∠DFE.
∵∠1=3∠2,∠2=24°,∴∠1=∠DFE=72°.
(2)不平行.理由如下:
∵∠E=48°,∠BFP=46°,∴∠E≠∠BFP.
∴CE与PF不平行.
方法归纳 本题考查平行线的判定与性质,解题的关键是:(1)得出AB∥CD.(2)熟悉平行线的判定定理.解决该类型题目时,根据相等(或互补)的角证出两直线平行是关键.
易错误区 判定两条直线平行,需要根据角的关系来判断,不能只凭观察得出结果.
例4 珠江流域某江段江水流向经过B,C,D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,求∠CDE的度数.
思路点拨 由已知可得AB∥DE,过点C作CF∥AB,由平行线的性质可得∠BCF+∠ABC=180°,所以能求出∠BCF,继而求出. 又由平行线的传递性得CF∥DE,所以∠CDE=∠DCF.
解题过程 如图,过点C作CF∥AB.∴∠BCF+∠ABC=180°.
∵∠ABC=120°,∴∠BCF=60°.
又∵∠BCD=80°,∴∠DCF=∠BCD-∠BCF=20°.
∵江水流向经过B,C,D三点拐弯后与原来相同,
∴AB∥DE.∴CF∥DE.∴∠CDE=∠DCF=20°.
方法归纳 本题考查的知识点是平行线的性质,关键是过点C先作AB的平行线,由平行线的性质求解.
易错误区 作辅助线只能作其中一条直线的平行线,然后利用传递性说明三条直线平行,不能出现过点C作CF∥AB∥DE的错误.
例5 如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD.
(2)若∠B=100°,点E,F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图2,求∠FAC的度数.
(3)若点 E 在直线 CD上,且满足 求∠ACD:∠AED的值(用含n的代数式表示).(请自己画出正确的图形,并解答)
思路点拨 (1)依据平行线的性质以及判定,即可得到AB∥CD.
(2)依据AC平分∠BAE,AF平分∠DAE,即可得到 进而得出 (3)分两种情况讨论:当点E在线段CD上时;当点E在DC的延长线上时,分别依据AB∥CD,得到 的值.
解题过程 (1)∵AD∥BC,∴∠A+∠B=180°.
又∵∠B=∠D,∴∠D+∠A=180°.∴AB∥CD.
∵AC平分∠BAE,AF平分∠DAE,
(3)分两种情况:
当点E在线段CD上时,如图3.
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又
当点E在DC的延长线上时,如图4.
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又∵∠EAC= ∠BAC,∴∠ACD:∠AED=n:(n-1).
方法归纳 本题主要考查平行线的性质以及判定,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
易错误区 (3)需要根据点E的位置分类讨论,是本题的难点和易错点,特别注意由于图形不确定,所以还要按要求画出图形,同时也考查几何作图能力.
探究 提升
例 探究:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗
(2)如图1,反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系 请证明.
(3)若将图1中的点E移至如图2所示的位置,此时∠B,∠D,∠E之间有什么关系 请证明.
(4)若将图1中的点E移至如图3所示的位置,情况又如何
(5)如图4,若AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系
(6)如图5,若AB∥CD,又得到什么结论
思路点拨已知AB∥CD,连接AB,CD的折线内折或外折、或改变点E的位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间.解题的关键是过点E或点F作AB(或CD)的平行线,把复杂的图形化归为基本图形.
解题过程 (1)过点E作EF∥AB,如图6,则∠B=∠BEF.
∵AB∥CD,∴EF∥CD.∴∠D=∠DEF.
∴∠BED=∠BEF+∠DEF=∠B+∠D.
(2)AB∥CD.理由如下:过点E作EF∥AB,如图6,则∠B=∠BEF.
∵∠BED=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF.∴EF∥CD.∴AB∥CD.
(3)∠BED+∠B+∠D=360°.理由如下:
若将点E移至如图2所示位置,过点E作EF∥AB,如图7.
∵AB∥CD,∴EF∥CD.
∴∠D+∠DEF=180°,∠B+∠BEF=180°.∴∠BED+∠B+∠D=360°.
(4)如图8,∵AB∥CD,∴∠B=∠BFD.
∵∠D+∠E+∠EFD=180°,∠BFD+∠EFD=180°,
∴∠D+∠E=∠BFD.∴∠D+∠E=∠B.
(5)如图9,过点F作. ,则由(1)的结论可知.
又∵∠EFG=∠EFH+∠HFG,∴∠E+∠G=∠B+∠EFG+∠D.
(6)由以上可知. .
方法归纳 本题考查了平行线的性质与判定,关键是添加适当的辅助线,把复杂的图形化归为基本图形,使问题得以简化.
易错误区 为了合理应用平行线的性质定理,过折点作平行线时画射线比较好,但要注意射线的方向,尽量避免添加辅助线后的图形复杂化.
专项训 练
拓展训练
A组
1.如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( ).
A.36° B.72°
C. 108° D. 118°
2.如图,三角形DEF经过怎样的平移可得三角形ABC( ).
A.先向左平移4个单位,再向下平移2个单位
B.先向右平移4个单位,再向下平移2个单位
C.先向右平移4个单位,再向上平移2个单位
D.先向左平移4个单位,再向上平移2个单位
3.【济南】如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( ).
A.20° B.35° C.55° D.70°
4.如图,. ,则∠4的度数为 .
5.将一副三角尺按如图所示摆放,边DE∥AB,则∠1= .
6.将一张长方形纸片折叠成如图的图形,若∠ABC=26°,则∠
7.如图,图1为北斗七星的位置图,图2将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=105°,则∠B-∠CGF= .
8.在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°(已知),
∴∠B=∠DCE( ).
又∵∠B=∠D( ),
∴∠DCE=∠D( ).
∴AD∥BE( ).
∴∠E=∠DFE( ).
9.潜望镜中的两面镜子MN和PQ是互相平行的,如图,光线AB经镜面反射后, 射入的光线AB与射出的光线CD平行吗 为什么
10.如图,已知AE⊥BC,FG⊥BC,∠1=∠2.
(1)求证:AE∥FG.
(2)求证:AB∥CD.
(3)若∠D=∠3+50°,∠CBD=80°,求∠C的度数.
B 组
11.如图,有两条长分别为a,b的铁丝,其中长为a的铁丝恰好围成一个大正方形;AB是大正方形的对角线,把AB分成n条相等的线段,再以每条线段作为小正方形的对角线,长为b的铁丝恰好能围成n个这样的小正方形.若均不考虑接口情况,则a,b的大小关系是( ).
A. a>b B. a12.【莱芜】如图,AB∥CD,∠BED=61°,∠ABE的平分线与∠CDE的平分线交于点F,则∠DFB等于( ).
A.149° B.149.5° C.150°
13.下列命题:①在同一平面内,过一点有且只有一条直线与已知直线垂直;②过一点有且只有一条直线与已知直线平行;③若b∥c,a∥c,则b∥a;④若∠1=40°,∠2的两边与∠1的两边分别平行,则∠2=40°或140°;⑤若b⊥c,a⊥c,则b∥a.其中是真命题的有 .(填序号)
14.如图,已知. CE平分 则 的度数为 .
15.如图, .求证:
16.如图,已知AB∥CD,点C在点D的右侧,BE平分. ,DE平分 BE,DE所在的直线交于点E,.
(1)求 的度数.
(2)若 ,求∠BED的度数(用含n的代数式表示).
(3)将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若 求∠BED的度数(用含n的代数式表示).
走进重高
1.【鞍山】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( ).
A.50° B.55° C.60° D.65°
2.【襄阳】如图,直线BC∥AE,CD⊥AB于点D,若∠BCD=40°,则∠1的度数是( ).
A.60° B.50° C.40° D.30°
3.【通辽】如图,∠AOB的一边OA为平面镜,∠AOB=37°45',在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
4.将一两边互相平行的纸带沿EF折叠,如图1, ,设∠AED'=x°.
(1)∠EFB= (用含x的代数式表示).
(2)若将图1继续沿BF折叠成图2,则. (用含x的代数式表示).
5.【武汉】如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
高分夺冠
1.如图,a∥b,设 下列说法中,正确的是( ).
A.若∠2=∠3,则.
B.若∠1=∠4,则.
C.若∠1=2∠2=2∠3,则.
D.若∠1=∠2=∠3,则.
2.如图,已知直线AB,CD被直线AC所截, E是平面内任意一点(点E不在直线AB,CD,AC上),设 β.下列各式:①α+β;②α-β;③β-α;④α/ -β;⑤360°-α-β.其中可以表示∠AEC度数的是 (填序号).
3.如图是某公园里一处长方形风景欣赏区ABCD,长AB=50m,宽BC=25m.为方便游人观赏,公园特意修建了如图所示的小路(图中非涂色部分),小路的宽均为1m,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为 m.
4.已知E,F分别是AB,CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD.
(2)如图2,若∠P=∠PFD-∠BEP,求证:AB∥CD.
(3)如图3,AB∥CD,移动点E,F使∠EPF=90°,作∠PEG=∠BEP,求 的值.
拓展训练
A组
1. C 2. A 3. B 4.78°5.105° 6.128°
7.115° 8.同旁内角互补,两直线平行 两直线平行,同位角相等 已知 等量代换 内错角相等,两直线平行 两直线平行,内错角相等
9.射入的光线AB与射出的光线CD平行.理由如下:∵MN∥PQ,
∴∠2=∠3(两直线平行,内错角相等).
又∵∠1=∠2,∠3=∠4,∴∠1+∠2=∠3+∠4.
,即∠5=∠6.
∴AB∥CD(内错角相等,两直线平行).
10.(1)∵AE⊥BC,FG⊥BC,∴AE∥FG.
(2)∵AE∥FG,∴∠1=∠CFG.
∵∠1=∠2,∴∠CFG=∠2.∴AB∥CD.
(3)∵AB∥CD,∴∠D+∠ABD=180°.
∴∠D+∠3+∠CBD=180°.
∵AB∥CD,∴∠C=∠3=25°.
B组
11. C 12. B 13.①③④ 14.100°
15.∵∠BAP+∠APD=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行).
∴∠BAP=∠APC(两直线平行,内错角相等).
又∵∠1=∠2(已知),∴∠FPA=∠EAP.
∴AE∥PF(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
16.(1)∵DE平分∠ADC,∠ADC=70°,
(2)∵BE平分∠ABC,
∵AB∥CD,∴∠BCD=∠ABC=n°.
∵∠CBE+∠BED=∠EDC+∠BCD,即
(3)如图,∵BE平分∠ABC,DE平分∠ADC,
∵AB∥CD,∴∠BAD+∠ADC=180°.
在四边形ADEB中,
走进重高
1. D 2. B 3.75°30′(或75.5°)
