浙教版(2019)高中信息技术 选修1 第3章 3.3.1 栈的概念、特性与基本操作 课件(共29张PPT)
文档属性
| 名称 | 浙教版(2019)高中信息技术 选修1 第3章 3.3.1 栈的概念、特性与基本操作 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
基础教育精品课
栈
2 栈的基本操作
1 栈的概念与特性
3 栈的应用实例
学习内容
大学
论语
中庸
孟子
将4本书依次放入收纳箱
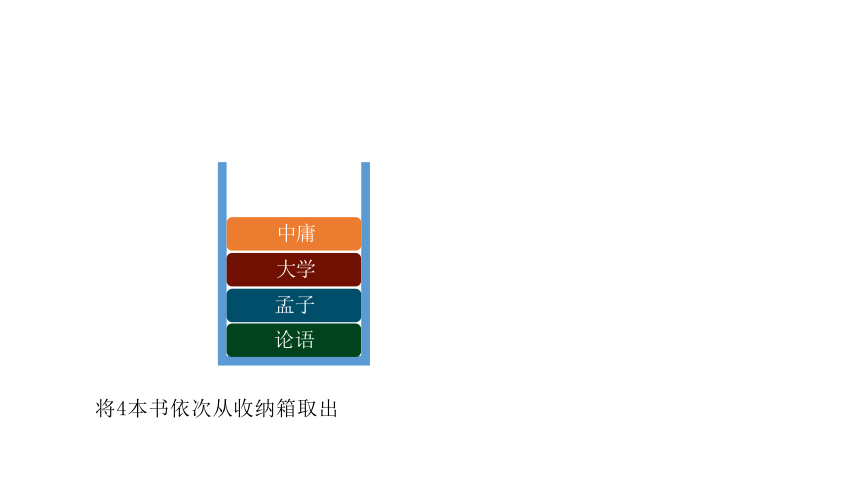
中庸
大学
孟子
论语
将4本书依次从收纳箱取出
弹匣中子弹装弹过程(入栈)
文字处理软件的“撤销 ”操作
网页浏览器的“ 后退 ”键
消毒桶中餐盘的取放
中庸
大学
孟子
论语
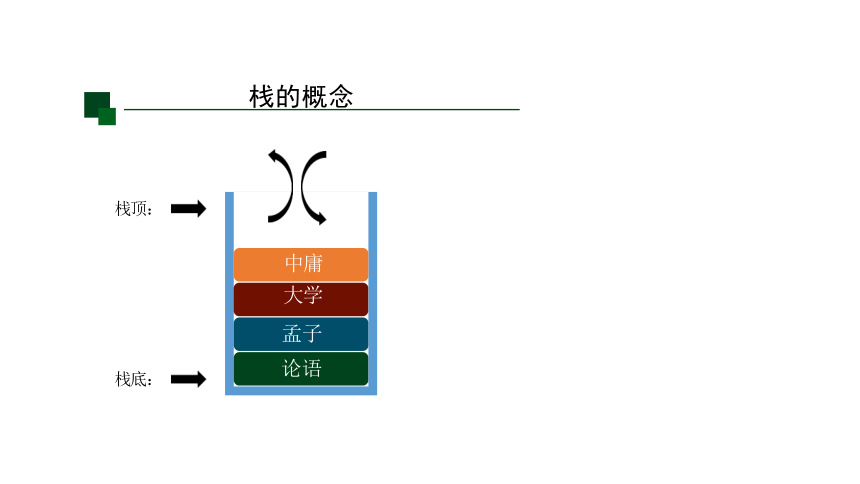
栈的概念
栈底:
栈顶:
中庸
大学
孟子
论语
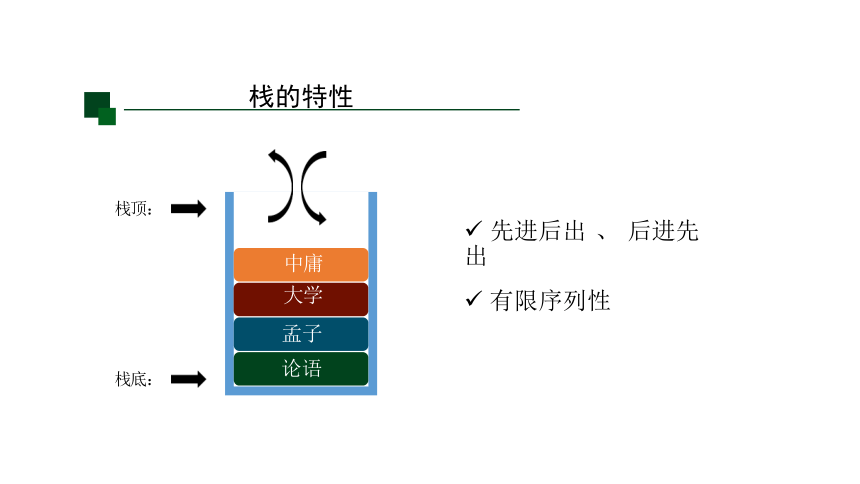
ü 先进后出 、 后进先出
ü 有限序列性
栈的特性
栈底:
栈顶:
相同点
有限序列, 线性表结构, 元素个数是有限的, 可以 是空的, 也可以包含多个 元素。
栈是“ 先进后出 ”, 仅在 栈顶 一 端进行入栈或出栈操作;
队列是“ 先进先出 ”, 可 以在两端进行操作, 其中队尾 一 端入队, 队首 一 端出队。
问题与讨论:栈与队列有什么相同点与不同点?
不同点
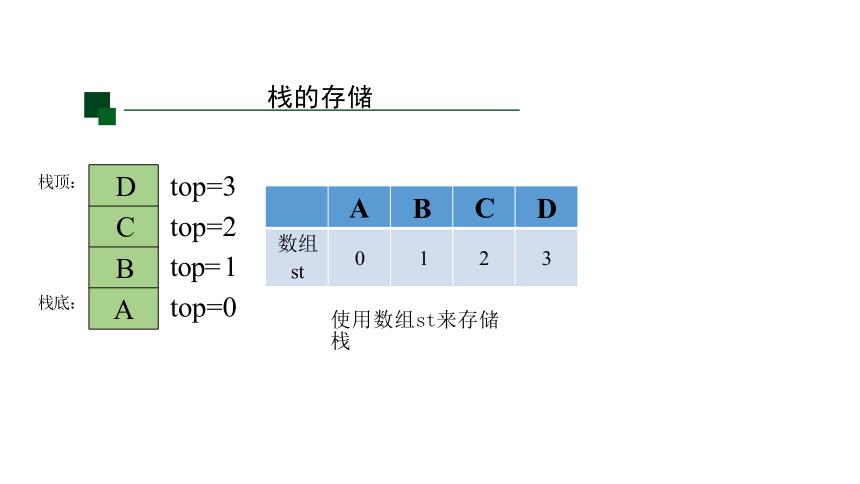
A B C
D
数组 st 0 1 2
3
D
C
B
A
栈的存储
top=3 top=2 top= 1 top=0
使用数组st来存储栈
栈底:
栈顶:
D
C
D
C
B
A
栈的存储
top=3 top=2 top= 1 top=0
B
A
^
栈的链式存储结构
栈底:
栈顶:
top
top = - 1
st = ['']*4
栈的基本操作:建栈
3
2
1
0
下标
空栈
top = top + 1 st[top] = 'A' top = top + 1 st[top] = 'B' top = top + 1 st[top] = 'C' top = top + 1 st[top] = 'D'
下标
3 2 1
top→ 0
栈的基本操作:入栈
D
C
B
A
C
B
A
B
A
A
3
top→ 2
1 0
top→ 3
2 1 0
3
2
top→ 1 0
① ② ③ ④
a = ['A','B','C','D'] for i in a:
=
D
C
B
A
栈的基本操作:入栈
3
2
1
0
下标
思考:
若栈空则不能出栈, 判断栈空的条件是什么?
下标
top→ 3
2
1
0
D
C
B
A
出栈时栈顶元素取出, 同时top值减1
栈的基本操作:出栈
出栈和取出栈顶元素有什么区别?
输出栈顶元素代码如何实现?
print(st[top])
top == - 1
while top > - 1:
print(st[top],end="") top = top - 1
下标
top→ 3
2
1
0
D
C
B
A
栈的基本操作:出栈
运行结果:
DCBA
问题与讨论:
字母A,B,C按顺序入栈, 请问出栈的顺序可能有哪几种?
A,B,C
A,C,B
B,A,C
B,C,A
C,B,A
C,A,B
A
B
C
问题与讨论:
字母A,B,C按顺序入栈, 请问出栈的顺序可能有哪几种?
B,C,A
C,B,A
C,A,B
A,B,C
A,C,B
B,A,C
A
B
C
第 一章项目挑战中的“ 用户角色特征值 ”, 把该值 (十进制) 转换成二进制, 采用“ 除 二取余法 ”, 利用
栈来存储每次计算得到的余数 。 (6)10 = (110)2
22
2
1
1
0
…
…
…
…
…
…
栈的实例:进制转换
2 top→1 0 入栈过程 top→2 1 0
2 6 2 3 2 1
0
栈的实例:进制转换
特征值的变化: 6→3→ 1→0
… …0
……1 ……1
2
1 top→ 0
0
1
0
1
1
0
n= 1 ②
n=0 ③
n=3 ①
2 2
1 1
top→ 0 0
top = - 1
② ③ ④
出栈过程
1 0
top→2
1
0
①
1
栈的实例:进制转换
1
0
0
1
1
0
2
top→1
0
stack = [- 1]* 100
top = - 1
n = int(input("请输入十进制整数:")) while :
x = n % 2
top = top + 1
n = n // 2
while top >= 0:
print(stack[top],end="")
=
栈的实例:进制转换
(6×(3+2)-4)÷2
6×(3+2)-4)÷2 (6×(3+2-4)÷2 )6×)3+2(-4(÷2
判断 一 个数学计算式中的括号(只有小括号) 是否匹配。
匹配
不匹配
不匹配
不匹配
栈的实例:括号匹配
括号的数量
括号的位置
从左往右遍历, 遇到左括号, 入栈, 遇到右括号, 出栈。
① 栈空, 出现右括号, 不匹配
② 遍历结束, 栈中还有左括号(栈不空), 不匹配 ③ 遍历结束, 栈空, 匹配
1.计算式中只关注括号, 忽略其他字符 ( ( ) ) 2.判断左右括号的数量与位置时, 采用栈结构来设计
栈的实例:括号匹配
第 一 步: 抽象与建模
(6×(3+2)-4)÷2
top = - 1
① ② ③ ④
栈的实例:括号匹配
第 二 步: 设计算法
( ( )
)
(
(
(
(
1
top→ 0
1
top→ 0
top→1
0
1
0
该字符是
右括号?
从左往右遍历
结束?
该字符是
左括号?
栈的实例:括号匹配
栈空?
栈空?
N Y
不匹配
不匹配
匹配
出栈
入栈
N
N
N
N
Y
Y
Y
Y
第三步: 编写程序
st = [""]* 100; top = - 1 #建栈 flag= True #标记是否有不匹配的情况 s = input("输入计算式:") for i in range(len(s)): #完善代码 if top >= 0: #栈中还有左括号 flag = False if flag: print("括号匹配") else: print("括号不匹配")
栈的实例:括号匹配
stacklist[] #建立 一 个空栈
stacklist.append("A") #字母A入栈
stacklist.append("B") #字母B入栈
print(stacklist[1]) #输出栈顶元素, 为字母B
print(len(stacklist)) #输出栈中元素个数, 为2
stacklist.pop() #弹出栈顶元素
print(len(stacklist)) #输出栈中元素个数, 为1, 是字母A
拓展:用列表自带函数和方法实现栈
小结与练习
1. 编号为1 、 2 、 3 、 4的4列火车, 按顺序开进 一 个栈式 结构的站点 。 开出火车站的顺序有多少种? 请写出所
有可能的出栈序列。
2. 元素a,b,c,d,e按序入栈, 在所有的出栈序列中, 以d 开 头的出栈序列有哪些?
3. 参照十进制转二进制的方法, 编写 一 个将十进制数N 转换为r进制数的程序。
4. 如果括号匹配问题中, 既有小括号 、 又有中括号和大 括号, 请你设计算法并编写程序判断括号是否匹配。
小结与练习
基础教育精品课
栈
2 栈的基本操作
1 栈的概念与特性
3 栈的应用实例
学习内容
大学
论语
中庸
孟子
将4本书依次放入收纳箱
中庸
大学
孟子
论语
将4本书依次从收纳箱取出
弹匣中子弹装弹过程(入栈)
文字处理软件的“撤销 ”操作
网页浏览器的“ 后退 ”键
消毒桶中餐盘的取放
中庸
大学
孟子
论语
栈的概念
栈底:
栈顶:
中庸
大学
孟子
论语
ü 先进后出 、 后进先出
ü 有限序列性
栈的特性
栈底:
栈顶:
相同点
有限序列, 线性表结构, 元素个数是有限的, 可以 是空的, 也可以包含多个 元素。
栈是“ 先进后出 ”, 仅在 栈顶 一 端进行入栈或出栈操作;
队列是“ 先进先出 ”, 可 以在两端进行操作, 其中队尾 一 端入队, 队首 一 端出队。
问题与讨论:栈与队列有什么相同点与不同点?
不同点
A B C
D
数组 st 0 1 2
3
D
C
B
A
栈的存储
top=3 top=2 top= 1 top=0
使用数组st来存储栈
栈底:
栈顶:
D
C
D
C
B
A
栈的存储
top=3 top=2 top= 1 top=0
B
A
^
栈的链式存储结构
栈底:
栈顶:
top
top = - 1
st = ['']*4
栈的基本操作:建栈
3
2
1
0
下标
空栈
top = top + 1 st[top] = 'A' top = top + 1 st[top] = 'B' top = top + 1 st[top] = 'C' top = top + 1 st[top] = 'D'
下标
3 2 1
top→ 0
栈的基本操作:入栈
D
C
B
A
C
B
A
B
A
A
3
top→ 2
1 0
top→ 3
2 1 0
3
2
top→ 1 0
① ② ③ ④
a = ['A','B','C','D'] for i in a:
=
D
C
B
A
栈的基本操作:入栈
3
2
1
0
下标
思考:
若栈空则不能出栈, 判断栈空的条件是什么?
下标
top→ 3
2
1
0
D
C
B
A
出栈时栈顶元素取出, 同时top值减1
栈的基本操作:出栈
出栈和取出栈顶元素有什么区别?
输出栈顶元素代码如何实现?
print(st[top])
top == - 1
while top > - 1:
print(st[top],end="") top = top - 1
下标
top→ 3
2
1
0
D
C
B
A
栈的基本操作:出栈
运行结果:
DCBA
问题与讨论:
字母A,B,C按顺序入栈, 请问出栈的顺序可能有哪几种?
A,B,C
A,C,B
B,A,C
B,C,A
C,B,A
C,A,B
A
B
C
问题与讨论:
字母A,B,C按顺序入栈, 请问出栈的顺序可能有哪几种?
B,C,A
C,B,A
C,A,B
A,B,C
A,C,B
B,A,C
A
B
C
第 一章项目挑战中的“ 用户角色特征值 ”, 把该值 (十进制) 转换成二进制, 采用“ 除 二取余法 ”, 利用
栈来存储每次计算得到的余数 。 (6)10 = (110)2
22
2
1
1
0
…
…
…
…
…
…
栈的实例:进制转换
2 top→1 0 入栈过程 top→2 1 0
2 6 2 3 2 1
0
栈的实例:进制转换
特征值的变化: 6→3→ 1→0
… …0
……1 ……1
2
1 top→ 0
0
1
0
1
1
0
n= 1 ②
n=0 ③
n=3 ①
2 2
1 1
top→ 0 0
top = - 1
② ③ ④
出栈过程
1 0
top→2
1
0
①
1
栈的实例:进制转换
1
0
0
1
1
0
2
top→1
0
stack = [- 1]* 100
top = - 1
n = int(input("请输入十进制整数:")) while :
x = n % 2
top = top + 1
n = n // 2
while top >= 0:
print(stack[top],end="")
=
栈的实例:进制转换
(6×(3+2)-4)÷2
6×(3+2)-4)÷2 (6×(3+2-4)÷2 )6×)3+2(-4(÷2
判断 一 个数学计算式中的括号(只有小括号) 是否匹配。
匹配
不匹配
不匹配
不匹配
栈的实例:括号匹配
括号的数量
括号的位置
从左往右遍历, 遇到左括号, 入栈, 遇到右括号, 出栈。
① 栈空, 出现右括号, 不匹配
② 遍历结束, 栈中还有左括号(栈不空), 不匹配 ③ 遍历结束, 栈空, 匹配
1.计算式中只关注括号, 忽略其他字符 ( ( ) ) 2.判断左右括号的数量与位置时, 采用栈结构来设计
栈的实例:括号匹配
第 一 步: 抽象与建模
(6×(3+2)-4)÷2
top = - 1
① ② ③ ④
栈的实例:括号匹配
第 二 步: 设计算法
( ( )
)
(
(
(
(
1
top→ 0
1
top→ 0
top→1
0
1
0
该字符是
右括号?
从左往右遍历
结束?
该字符是
左括号?
栈的实例:括号匹配
栈空?
栈空?
N Y
不匹配
不匹配
匹配
出栈
入栈
N
N
N
N
Y
Y
Y
Y
第三步: 编写程序
st = [""]* 100; top = - 1 #建栈 flag= True #标记是否有不匹配的情况 s = input("输入计算式:") for i in range(len(s)): #完善代码 if top >= 0: #栈中还有左括号 flag = False if flag: print("括号匹配") else: print("括号不匹配")
栈的实例:括号匹配
stacklist[] #建立 一 个空栈
stacklist.append("A") #字母A入栈
stacklist.append("B") #字母B入栈
print(stacklist[1]) #输出栈顶元素, 为字母B
print(len(stacklist)) #输出栈中元素个数, 为2
stacklist.pop() #弹出栈顶元素
print(len(stacklist)) #输出栈中元素个数, 为1, 是字母A
拓展:用列表自带函数和方法实现栈
小结与练习
1. 编号为1 、 2 、 3 、 4的4列火车, 按顺序开进 一 个栈式 结构的站点 。 开出火车站的顺序有多少种? 请写出所
有可能的出栈序列。
2. 元素a,b,c,d,e按序入栈, 在所有的出栈序列中, 以d 开 头的出栈序列有哪些?
3. 参照十进制转二进制的方法, 编写 一 个将十进制数N 转换为r进制数的程序。
4. 如果括号匹配问题中, 既有小括号 、 又有中括号和大 括号, 请你设计算法并编写程序判断括号是否匹配。
小结与练习
