浙教版(2019)高中信息技术 选修1 第5章 5.2.1 迭代 课件(共27张PPT)
文档属性
| 名称 | 浙教版(2019)高中信息技术 选修1 第5章 5.2.1 迭代 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2024-05-08 10:30:40 | ||
图片预览






文档简介
(共27张PPT)
5.2 迭 代 与 递 归 (一)
—— 迭 代
册 别:选择性必修1
学 科:高中信息技术(浙教版)
学习目标:
能理解迭代的算法思想。
能合理选用数据结构,理清迭代初值,迭代式及结束迭代。
能用自然语言、流程图、Python语言描述迭代算法。
能分析迭代算法的效率高低。
能熟练应用迭代算法,解决生活、学习中的问题。
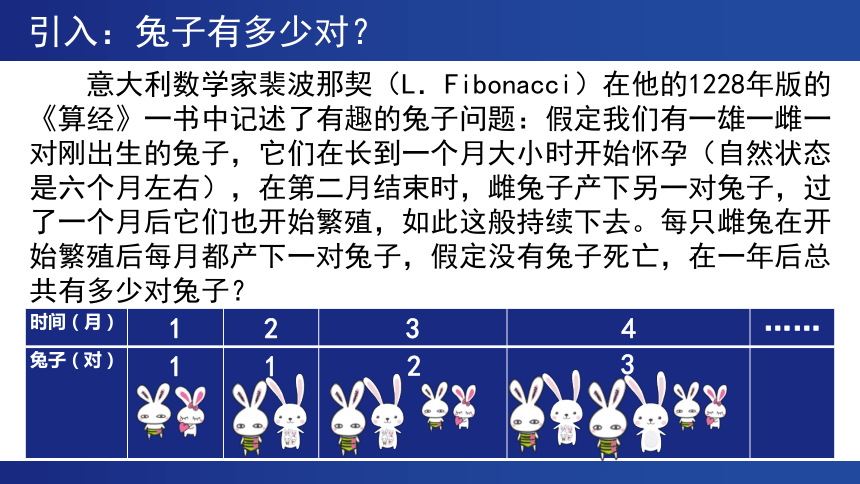
引入:兔子有多少对?
意大利数学家裴波那契(L.Fibonacci)在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定我们有一雄一雌一对刚出生的兔子,它们在长到一个月大小时开始怀孕(自然状态是六个月左右),在第二月结束时,雌兔子产下另一对兔子,过了一个月后它们也开始繁殖,如此这般持续下去。每只雌兔在开始繁殖后每月都产下一对兔子,假定没有兔子死亡,在一年后总共有多少对兔子?
时间(月) 1 2 3 4 ……
兔子(对) 1 1
2
3
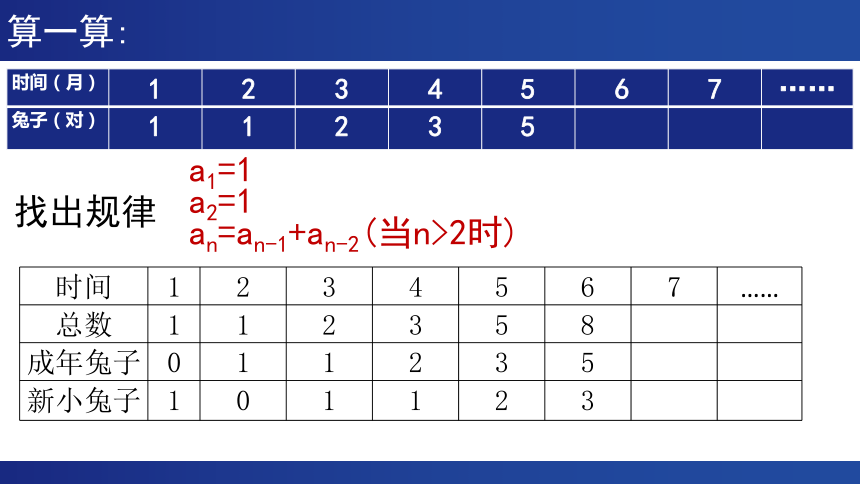
算一算:
时间(月) 1 2 3 4 5 6 7 ……
兔子(对) 1 1 2 3 5
找出规律
时间 1 2 3 4 5 6 7 ……
总数 1 1 2 3 5 8
成年兔子 0 1 1 2 3 5
新小兔子 1 0 1 1 2 3
a1=1
a2=1
an=an-1+an-2(当n>2时)
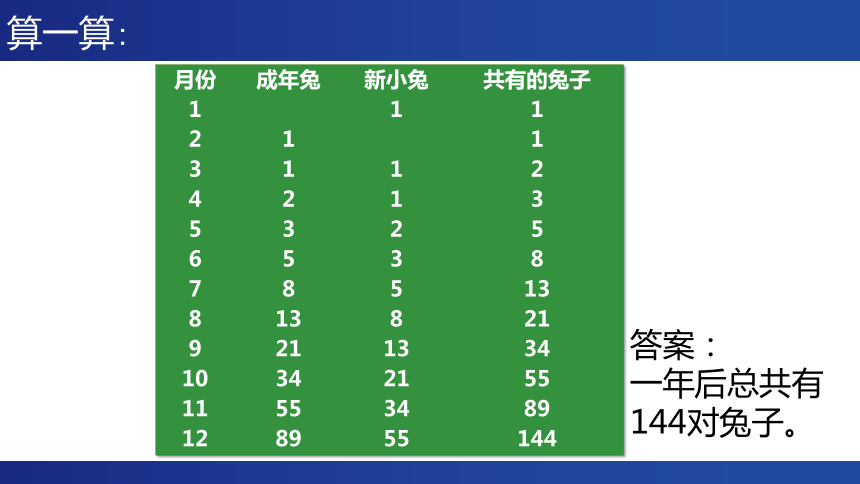
算一算:
月份 成年兔 新小兔 共有的兔子
1 1 1
2 1 1
3 1 1 2
4 2 1 3
5 3 2 5
6 5 3 8
7 8 5 13
8 13 8 21
9 21 13 34
10 34 21 55
11 55 34 89
12 89 55 144
答案:
一年后总共有144对兔子。
裴波那契数列:
裴波那契数为:1,1,2,3,5,8,13 其规律是:数列中第1,2个数都是1,从第三个数起,该数是前面2个数之和,此数列称为Fibonacci数列。
第n项计算公式为:Fib(n)=1 (n<=2)
Fib(n)=Fib(n-1)+Fib(n-2) (n>2)
因此从第三个元素开始循环,
Fib(3)=Fib(1)+Fib(2)
Fib(4)=Fib(2)+Fib(3)
Fib(5)=Fib(3)+Fib(4)
……
程序实现(一):
a=[1,1]
for i in range(2,12):
a.append(0)
a[i]=a[i-1]+a[i-2]
print(a[11])
#定义列表a为每个月的兔子对数,第1,2月的兔子数量为1对
#对第3个月至第12月逐一计算兔子对数
#a最后添加一个初值为0的元素,存第i个月兔子数
#求出第i个月的兔子对数(迭代表达式)
#输出第12月的兔子对数
12个月的兔子对数用a数组(a列表)来存储
程序实现(二):
a = 1
b = 1
for i in range(2,12):
c = a + b
a = b
b = c
print(c)
#定义a,b为第1月,第2月的兔子数量为1对
#对第3个月至第12月每月计算兔子对数
#当前一个月的值b迭代前两个月的值a
#当月的值c迭代前一个月的值b
#输出第12月的兔子对数
#从第3个月起兔子对数为前面两个月的兔子对数之和
a,b,c三个变量存储近三个月的兔子数
迭代算法的概念:
迭代是重复反馈的活动,其目的通常是为了使结果符合目标需求。
开发产品
反复修改
符合客户需求
让计算机重复执行一组指令(或步骤),这组指令(或步骤)每执行一次时,都会让变量从原值递推出一个新值。
迭代算法三个方面:
1、确定迭代变量
2、建立迭代关系
3、控制迭代过程
一个直接或间接地不断由旧值递推出新值的变量;
将变量从前一个值推出其下一个值的公式(或关系);
设定迭代结束的条件。
a = 1
b = 1
for i in range(3,13):
c = a + b
a = b
b = c
print(c)
1、确定迭代变量
a( 前2个月),b(前1个月)
2、建立迭代关系:从第3个月
起兔子对数为前面两个月的兔
子对数之和。
1、确定迭代变量
a( 前2个月),b(前1个月)
3、设定迭代第3至第12月
迭代法求a的平方根: 教材P119
基本思路:先估测一个近似值x,然后不断令x等于x和的平均数(迭代公式为: (n≥0)),经过若干次迭代后,x的值将逐渐接近a的平方根(当与值无限接近时,可看作= ,则公式 可以化简为=, 就是a的平方根)
迭代式:是什么
可终止的条件是什么
1、确定迭代变量:
2、建立迭代关系:
3、控制迭代过程:
X,初始值:是什么
迭代法求a的平方根: 教材P119
基本思路:先估测一个近似值x,然后不断令x等于x和的平均数(迭代公式为: (n≥0)),经过若干次迭代后,x的值将逐渐接近a的平方根(当与值无限接近时,可看作= ,则公式 可以化简为=, 就是a的平方根)
迭代式:是什么
可终止的条件是什么
1、确定迭代变量:
2、建立迭代关系:
3、控制迭代过程:
X,初始值:是什么
=
迭代变量x的迭代过程:
迭代次数 xn xn+1 ▏xn+1-xn ▏
1 1 1.5 0.5
2 1.5 1.416667 0.083333
3 1.416667 1.414216 0.002451
4 1.414216 1.414214 0.000002
当前后两次求出的x值(xn+1和xn)的差的绝对值( ▏xn+1-xn ▏)
为0.000002时(即 ▏xn+1-xn ▏<=0.00001) 停止迭代,得出结果。如2的平方根约为1.414214。
(1)抽象建模
x0
x1
x1
x2
x2
x3
x3
x4
(2)设计算法
求平方根迭代程序流程图
开始
(1)输入a, 求x估测近似值
x0=a;x1=(x0+a/x0)/2
①若〡x1-x0〡>10-5
②迭代式x0=x1
x1=(x0+a/x0)/2
③否则〡x1-x0〡<=10-5
④输出a 的平方根x1
〡x1-x0〡>0.00001
输入a
输出平方根x1
x0=x1;x1=(x0+a/x0)/2
结束
N
Y
(2)迭代求平方根
x0=a;x1=(x0+a/x0)/2
编写求平方根迭代程序并上机调试:
#程序一:
a=int(input("请输入一个需要求其平方根的数:"))
x0=a
x1=(x0+a/x0)/2
while (abs(x1-x0))>0.00001:
x0=x1
x1=(x0+a/x0)/2
print(a,"的平方根约为",round(x1,6))
(3)编写程序并调试
牛顿迭代法计算正数a的算术根
#X0,初始值a
#X1,迭代式
#X1与x0无限接近,相差0.00001
#X0由X1迭代
#X1,迭代式
#X1为a的平方根
在保留小数位数不同的情况下,程序效率差异也大
#程序二:
a=int(input("请输入一个需要求其平方根的数:"))
x=a/2
while ((abs((x+a/x)/2-x))>0.00001):
x=(x+a/x)/2
print(a,"的平方根约为",round((x+a/x)/2,6))
(3)编写程序并调试
#X0,初始值a/2
#X1与x0无限接近,相差0.00001
#X0迭代式
#(x+a/x)/2为a的平方根
编写求平方根迭代程序并上机调试:
#程序三:
a=int(input("请输入一个需要求其平方根的数:"))
x=a/2
while abs(x*x-a) > 1e-5:
x=(x+a/x)/2
print(a,"的平方根约为",round((x+a/x)/2,6))
(3)编写程序并调试
#平方根X的初始值a/2
#X*X与a无限接近,相差0.00001
#X迭代式
#(x+a/x)/2为a的平方根
影响迭代算法的因素:
终止条件的设置
初始值不同
x0=a或x0=a/2
(abs(x1-x0))>0.00001
(保留5位小数位数)
(abs(x1-x0))>0.000001
(保留6位小数位数)
初始值、终止条件等直接影响算法效率
课堂小练:
利用欧几里得算法求最大公约数的python程序,其中m和n是迭代变量,迭代关系是n→m和m%n→n,由旧值推出新值,然后循环执行,直到余数为0,结束迭代。
m=int(input("请输入数m:"))
n=int(input("请输入数n:"))
while n!=0:
t=n
m=t
print( )
1.完善划线处代码:
n=m%n
m
课堂小练:
一个楼梯有n阶,上楼可以一步上一阶,也可以一步上二阶。要求:编写一个程序,输入一个正整数n(表示楼梯阶数),输出共有多少种不同的走法可以到达第n阶。
2.程序设计并调试:
f(n)=
1 n=1
2 n=2
f(n-1)+f(n-2) n>=3
课堂小练:
2.程序设计并调试:
n=int(input("请输入台阶数量:"))
a=1;b=2
for i in range(3,n+1):
c=a+b
a=b
b=c
if n==1 or n==2:
print(n)
else:
print(c)
生活实战应用:秋游安排车辆
某班家委会根据参加秋游的同学到达指定上车点时间和每位同学可以等待的时间信息,安排车辆接送参加秋游活动同学去秋游点白云山脚(考虑车子座位数量<=4人)。参加秋游活动同学到达上车点的时间和可以等待的时间用长度为7的字符串表示,例如out.txt中第一行“ 08:11 4 xixi”表示xixi同学当天8点11分到达上车点,最多等待4分钟(每个同学的等待时间都小于10),那么最晚8点23分出发去秋游点(若8点23分刚到的同学也一同出发)。编写 Python 程序,统计接送n个参加秋游活动同学所需的最少车辆数。运行程序,显示所有同学提交的信息,数据已经按到达时间先后排列,程序运行结果显示所需的最少车辆数。
A
(1)若将图中第 1 行“08:11 4”数据改为“08:11 2”,程序输出的结果是否会发生改变 (A.会改变 B.不会改变)
生活实战应用:安排车辆
(2)实现上述功能的部分 Python 程序如下,请在划线处填入合适的代码。
a=[];b=[];c=[];xz=4 #每辆车最多坐4人
#从文件out.txt中读取每一行数据在列表a中,n为参加秋游人数,代码略
for i in range(n):
b.append(0);c.append(0)
b[i]=int(a[i][:2])*60+int(a[i][3:5])
c[i]=b[i]+int(a[i][6:8])
tot=0;i=0;k=1
while i#①
j=i+1
while jif b[j]<=t:
k+=1;j+=1
else:
break
if k==xz:k=0;break
#②
tot+=1
for i in range(n):print(a[i])
print("接送所有参加秋游同学最少需要",tot,"辆车")
②i=j
①t=c[i]
这个for循环求出到指定地点的时间b列表,最迟离开时间c列表
tot为接送所有参加秋游同学最少需要车辆数
外循环求出当前i同学最迟离开时间c[i]前与最早离开j同学同一辆车拼车过程
内循环求出当前i同学最迟离开时间c[i]前与最早离开j同学b[j]同一辆车不超过4人的拼车过程,若拼不成,j同学为另起一辆车
课堂小结
迭代算法的概念
算法思想 算法描述
迭代算法的三要素
迭代算法的数学原理与注意事项
程序实现
学习评价
对自己的表现进行客观的评价,并思考后续完善的方向。(3=优秀,2=一般,1=仍需加油)
评分项 自我评价
能计算兔子对数问题并总结迭代算法的基本思想 3 2 1
掌握迭代算法的三要素 3 2 1
能自主学习教材并用自然语言、流程图描述迭代算法 3 2 1
能够用Python语言描述迭代算法 3 2 1
能够编程实现牛顿迭代法求根 3 2 1
能理解牛顿迭代法的数学原理、注意事项 3 2 1
能用迭代算法完成学习、生活中的应用 3 2 1
课后作业
1.操作系统从win xp、win7、win10……,不断更新过程可以看出,一款产品是不断试错,不断根据用户体验反馈,快速调整和完善得到的。这个例子体现的算法思想是 ( )
A.枚举 B.迭代 C.解析 D.递归
2.利用迭代算法处理问题,需要考虑以下三个方面:
①确定迭代变量:一个直接或间接地不断由旧值递推出新值的变量;
② :将变量从前一个值推出其下一个值的公式(或关系);
③控制迭代过程:设定迭代结束的条件。
建立迭代关系式
B
课后作业
3.在程序划线处填空题:圆周率其实就是一个圆周长与直径的比值我们通常用希腊字母π表示,其中用莱布尼茨公式是这样的:
小新用迭代法编写了一个Python程序用于求圆周率Pi,请完善程序(精确到小数点后6位)。
i=1;s=0;k=1
ans=0
while ① :
ans+=1
s+=k*1/i
i+=2
②
print("pi=",s*4)
print(迭代次数:",ans)
1/i>=0.00000001
1/i>=0.000001
k=-k
若要精确到小数点后8位,①空如何填写?
5.2 迭 代 与 递 归 (一)
—— 迭 代
册 别:选择性必修1
学 科:高中信息技术(浙教版)
学习目标:
能理解迭代的算法思想。
能合理选用数据结构,理清迭代初值,迭代式及结束迭代。
能用自然语言、流程图、Python语言描述迭代算法。
能分析迭代算法的效率高低。
能熟练应用迭代算法,解决生活、学习中的问题。
引入:兔子有多少对?
意大利数学家裴波那契(L.Fibonacci)在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定我们有一雄一雌一对刚出生的兔子,它们在长到一个月大小时开始怀孕(自然状态是六个月左右),在第二月结束时,雌兔子产下另一对兔子,过了一个月后它们也开始繁殖,如此这般持续下去。每只雌兔在开始繁殖后每月都产下一对兔子,假定没有兔子死亡,在一年后总共有多少对兔子?
时间(月) 1 2 3 4 ……
兔子(对) 1 1
2
3
算一算:
时间(月) 1 2 3 4 5 6 7 ……
兔子(对) 1 1 2 3 5
找出规律
时间 1 2 3 4 5 6 7 ……
总数 1 1 2 3 5 8
成年兔子 0 1 1 2 3 5
新小兔子 1 0 1 1 2 3
a1=1
a2=1
an=an-1+an-2(当n>2时)
算一算:
月份 成年兔 新小兔 共有的兔子
1 1 1
2 1 1
3 1 1 2
4 2 1 3
5 3 2 5
6 5 3 8
7 8 5 13
8 13 8 21
9 21 13 34
10 34 21 55
11 55 34 89
12 89 55 144
答案:
一年后总共有144对兔子。
裴波那契数列:
裴波那契数为:1,1,2,3,5,8,13 其规律是:数列中第1,2个数都是1,从第三个数起,该数是前面2个数之和,此数列称为Fibonacci数列。
第n项计算公式为:Fib(n)=1 (n<=2)
Fib(n)=Fib(n-1)+Fib(n-2) (n>2)
因此从第三个元素开始循环,
Fib(3)=Fib(1)+Fib(2)
Fib(4)=Fib(2)+Fib(3)
Fib(5)=Fib(3)+Fib(4)
……
程序实现(一):
a=[1,1]
for i in range(2,12):
a.append(0)
a[i]=a[i-1]+a[i-2]
print(a[11])
#定义列表a为每个月的兔子对数,第1,2月的兔子数量为1对
#对第3个月至第12月逐一计算兔子对数
#a最后添加一个初值为0的元素,存第i个月兔子数
#求出第i个月的兔子对数(迭代表达式)
#输出第12月的兔子对数
12个月的兔子对数用a数组(a列表)来存储
程序实现(二):
a = 1
b = 1
for i in range(2,12):
c = a + b
a = b
b = c
print(c)
#定义a,b为第1月,第2月的兔子数量为1对
#对第3个月至第12月每月计算兔子对数
#当前一个月的值b迭代前两个月的值a
#当月的值c迭代前一个月的值b
#输出第12月的兔子对数
#从第3个月起兔子对数为前面两个月的兔子对数之和
a,b,c三个变量存储近三个月的兔子数
迭代算法的概念:
迭代是重复反馈的活动,其目的通常是为了使结果符合目标需求。
开发产品
反复修改
符合客户需求
让计算机重复执行一组指令(或步骤),这组指令(或步骤)每执行一次时,都会让变量从原值递推出一个新值。
迭代算法三个方面:
1、确定迭代变量
2、建立迭代关系
3、控制迭代过程
一个直接或间接地不断由旧值递推出新值的变量;
将变量从前一个值推出其下一个值的公式(或关系);
设定迭代结束的条件。
a = 1
b = 1
for i in range(3,13):
c = a + b
a = b
b = c
print(c)
1、确定迭代变量
a( 前2个月),b(前1个月)
2、建立迭代关系:从第3个月
起兔子对数为前面两个月的兔
子对数之和。
1、确定迭代变量
a( 前2个月),b(前1个月)
3、设定迭代第3至第12月
迭代法求a的平方根: 教材P119
基本思路:先估测一个近似值x,然后不断令x等于x和的平均数(迭代公式为: (n≥0)),经过若干次迭代后,x的值将逐渐接近a的平方根(当与值无限接近时,可看作= ,则公式 可以化简为=, 就是a的平方根)
迭代式:是什么
可终止的条件是什么
1、确定迭代变量:
2、建立迭代关系:
3、控制迭代过程:
X,初始值:是什么
迭代法求a的平方根: 教材P119
基本思路:先估测一个近似值x,然后不断令x等于x和的平均数(迭代公式为: (n≥0)),经过若干次迭代后,x的值将逐渐接近a的平方根(当与值无限接近时,可看作= ,则公式 可以化简为=, 就是a的平方根)
迭代式:是什么
可终止的条件是什么
1、确定迭代变量:
2、建立迭代关系:
3、控制迭代过程:
X,初始值:是什么
=
迭代变量x的迭代过程:
迭代次数 xn xn+1 ▏xn+1-xn ▏
1 1 1.5 0.5
2 1.5 1.416667 0.083333
3 1.416667 1.414216 0.002451
4 1.414216 1.414214 0.000002
当前后两次求出的x值(xn+1和xn)的差的绝对值( ▏xn+1-xn ▏)
为0.000002时(即 ▏xn+1-xn ▏<=0.00001) 停止迭代,得出结果。如2的平方根约为1.414214。
(1)抽象建模
x0
x1
x1
x2
x2
x3
x3
x4
(2)设计算法
求平方根迭代程序流程图
开始
(1)输入a, 求x估测近似值
x0=a;x1=(x0+a/x0)/2
①若〡x1-x0〡>10-5
②迭代式x0=x1
x1=(x0+a/x0)/2
③否则〡x1-x0〡<=10-5
④输出a 的平方根x1
〡x1-x0〡>0.00001
输入a
输出平方根x1
x0=x1;x1=(x0+a/x0)/2
结束
N
Y
(2)迭代求平方根
x0=a;x1=(x0+a/x0)/2
编写求平方根迭代程序并上机调试:
#程序一:
a=int(input("请输入一个需要求其平方根的数:"))
x0=a
x1=(x0+a/x0)/2
while (abs(x1-x0))>0.00001:
x0=x1
x1=(x0+a/x0)/2
print(a,"的平方根约为",round(x1,6))
(3)编写程序并调试
牛顿迭代法计算正数a的算术根
#X0,初始值a
#X1,迭代式
#X1与x0无限接近,相差0.00001
#X0由X1迭代
#X1,迭代式
#X1为a的平方根
在保留小数位数不同的情况下,程序效率差异也大
#程序二:
a=int(input("请输入一个需要求其平方根的数:"))
x=a/2
while ((abs((x+a/x)/2-x))>0.00001):
x=(x+a/x)/2
print(a,"的平方根约为",round((x+a/x)/2,6))
(3)编写程序并调试
#X0,初始值a/2
#X1与x0无限接近,相差0.00001
#X0迭代式
#(x+a/x)/2为a的平方根
编写求平方根迭代程序并上机调试:
#程序三:
a=int(input("请输入一个需要求其平方根的数:"))
x=a/2
while abs(x*x-a) > 1e-5:
x=(x+a/x)/2
print(a,"的平方根约为",round((x+a/x)/2,6))
(3)编写程序并调试
#平方根X的初始值a/2
#X*X与a无限接近,相差0.00001
#X迭代式
#(x+a/x)/2为a的平方根
影响迭代算法的因素:
终止条件的设置
初始值不同
x0=a或x0=a/2
(abs(x1-x0))>0.00001
(保留5位小数位数)
(abs(x1-x0))>0.000001
(保留6位小数位数)
初始值、终止条件等直接影响算法效率
课堂小练:
利用欧几里得算法求最大公约数的python程序,其中m和n是迭代变量,迭代关系是n→m和m%n→n,由旧值推出新值,然后循环执行,直到余数为0,结束迭代。
m=int(input("请输入数m:"))
n=int(input("请输入数n:"))
while n!=0:
t=n
m=t
print( )
1.完善划线处代码:
n=m%n
m
课堂小练:
一个楼梯有n阶,上楼可以一步上一阶,也可以一步上二阶。要求:编写一个程序,输入一个正整数n(表示楼梯阶数),输出共有多少种不同的走法可以到达第n阶。
2.程序设计并调试:
f(n)=
1 n=1
2 n=2
f(n-1)+f(n-2) n>=3
课堂小练:
2.程序设计并调试:
n=int(input("请输入台阶数量:"))
a=1;b=2
for i in range(3,n+1):
c=a+b
a=b
b=c
if n==1 or n==2:
print(n)
else:
print(c)
生活实战应用:秋游安排车辆
某班家委会根据参加秋游的同学到达指定上车点时间和每位同学可以等待的时间信息,安排车辆接送参加秋游活动同学去秋游点白云山脚(考虑车子座位数量<=4人)。参加秋游活动同学到达上车点的时间和可以等待的时间用长度为7的字符串表示,例如out.txt中第一行“ 08:11 4 xixi”表示xixi同学当天8点11分到达上车点,最多等待4分钟(每个同学的等待时间都小于10),那么最晚8点23分出发去秋游点(若8点23分刚到的同学也一同出发)。编写 Python 程序,统计接送n个参加秋游活动同学所需的最少车辆数。运行程序,显示所有同学提交的信息,数据已经按到达时间先后排列,程序运行结果显示所需的最少车辆数。
A
(1)若将图中第 1 行“08:11 4”数据改为“08:11 2”,程序输出的结果是否会发生改变 (A.会改变 B.不会改变)
生活实战应用:安排车辆
(2)实现上述功能的部分 Python 程序如下,请在划线处填入合适的代码。
a=[];b=[];c=[];xz=4 #每辆车最多坐4人
#从文件out.txt中读取每一行数据在列表a中,n为参加秋游人数,代码略
for i in range(n):
b.append(0);c.append(0)
b[i]=int(a[i][:2])*60+int(a[i][3:5])
c[i]=b[i]+int(a[i][6:8])
tot=0;i=0;k=1
while i
j=i+1
while j
k+=1;j+=1
else:
break
if k==xz:k=0;break
#②
tot+=1
for i in range(n):print(a[i])
print("接送所有参加秋游同学最少需要",tot,"辆车")
②i=j
①t=c[i]
这个for循环求出到指定地点的时间b列表,最迟离开时间c列表
tot为接送所有参加秋游同学最少需要车辆数
外循环求出当前i同学最迟离开时间c[i]前与最早离开j同学同一辆车拼车过程
内循环求出当前i同学最迟离开时间c[i]前与最早离开j同学b[j]同一辆车不超过4人的拼车过程,若拼不成,j同学为另起一辆车
课堂小结
迭代算法的概念
算法思想 算法描述
迭代算法的三要素
迭代算法的数学原理与注意事项
程序实现
学习评价
对自己的表现进行客观的评价,并思考后续完善的方向。(3=优秀,2=一般,1=仍需加油)
评分项 自我评价
能计算兔子对数问题并总结迭代算法的基本思想 3 2 1
掌握迭代算法的三要素 3 2 1
能自主学习教材并用自然语言、流程图描述迭代算法 3 2 1
能够用Python语言描述迭代算法 3 2 1
能够编程实现牛顿迭代法求根 3 2 1
能理解牛顿迭代法的数学原理、注意事项 3 2 1
能用迭代算法完成学习、生活中的应用 3 2 1
课后作业
1.操作系统从win xp、win7、win10……,不断更新过程可以看出,一款产品是不断试错,不断根据用户体验反馈,快速调整和完善得到的。这个例子体现的算法思想是 ( )
A.枚举 B.迭代 C.解析 D.递归
2.利用迭代算法处理问题,需要考虑以下三个方面:
①确定迭代变量:一个直接或间接地不断由旧值递推出新值的变量;
② :将变量从前一个值推出其下一个值的公式(或关系);
③控制迭代过程:设定迭代结束的条件。
建立迭代关系式
B
课后作业
3.在程序划线处填空题:圆周率其实就是一个圆周长与直径的比值我们通常用希腊字母π表示,其中用莱布尼茨公式是这样的:
小新用迭代法编写了一个Python程序用于求圆周率Pi,请完善程序(精确到小数点后6位)。
i=1;s=0;k=1
ans=0
while ① :
ans+=1
s+=k*1/i
i+=2
②
print("pi=",s*4)
print(迭代次数:",ans)
1/i>=0.00000001
1/i>=0.000001
k=-k
若要精确到小数点后8位,①空如何填写?
