1.3 二元一次方程组的应用 课件 (共24张PPT) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 1.3 二元一次方程组的应用 课件 (共24张PPT) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 21:09:23 | ||
图片预览








文档简介
(共24张PPT)
第1章 有理数
1.3(第1课时) 二元一次方程组
的应用(1)
学习目标
1.会根据问题情境及条件列出二元一次方程组,解方 组,并检验解是否合理;(重点)
2.通过解决实际问题进一步体会方程建模的过程和作用.
3.寻找等量关系.(难点)
新课导入
动脑筋
“鸡兔同笼”是我国古代著名的数学趣题之一. 大约在1500年前成书的《孙子算经》中就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?” 这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有 35 个头;从下面数,有 94 条腿. 问笼中各有几只鸡和兔?
本题涉及的等量关系有:
鸡头数+兔头数=35,
鸡的腿数+兔子的腿数=94.
设鸡有x只,兔有y只.
根据等量关系,得
解这个方程组,得
答:笼中有23只鸡,12只兔.
【例1】某业余运动员针对自行车和长跑项目进行专项训练.某次训练中,他骑自行车的平均速度为10m/s,跑步的平均速度为 m/s,自行车路段和长跑路段共5km,共用时15min.求自行车路段和长跑路段的长度.
分析 本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
解 设自行车路段的长度为x m,长跑路段的长度为y m.
根据等量关系,得
解这个方程组,得
因此自行车路段长度为3000m,长跑路段的长度为2000m.
【例2】某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的甲乙两种配料. 用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克
分析 本问题涉及的等量关系有:
甲配料质量+乙配料质量=总质量,
甲配料含蛋白质质量+乙配料含蛋白质质量=总蛋白质质量.
解 设含蛋白质20%的配料需用x kg,含蛋白质12%的配料需用y kg.
根据等量关系,得
解这个方程组,得
答:可以配制出所要求的食品,其中含蛋白质20%的配料需用37.5kg,含蛋白质12%的配料需用62.5kg.
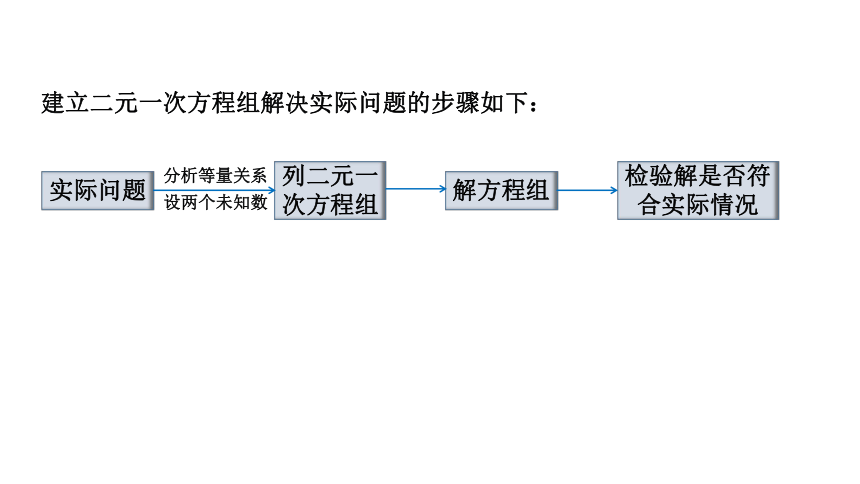
建立二元一次方程组解决实际问题的步骤如下:
实际问题
列二元一次方程组
解方程组
检验解是否符合实际情况
分析等量关系
设两个未知数
练习
1.植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵,求男生、女生各有多少人?
解:设男生有x人,女生有y人.
根据等量关系,得
解这个方程组,得
答:男生有12人,女生有8人.
2.某班去看演出,甲种票每张24元,乙种票每张18元,如果35名同学购票恰好用去750元,求甲、乙两种票各买了多少张?
解:设甲种票买了x张,乙种票买了y张.
根据等量关系,得
解这个方程组,得
答:甲种票买了20张,乙种票买了15张.
课堂小结
列方程组解决问题
关键:找等量关系
一般步骤:
审、设、列、解、验、答
第1章 有理数
1.3(第2课时) 二元一次方程组的应用(2)
学习目标
1.会根据问题情境及条件列出二元一次方程组,解方 组,并检验解是否合理;(重点)
2.通过解决实际问题进一步体会方程建模的过程和作用.
3.寻找等量关系.(难点)
新课导入
动脑筋
小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需要10min,从学校到家里需15min.问小华家离学校多远?
小华家到学校的路程分为两段:平路与坡路(回家所走的上坡路长即为去学校的下坡路长).根据问题中涉及的路程、速度与时间的数量关系,可得
从家到学校
从学校到家
走平路的时间+走下坡路的时间=10min,
走上坡路的时间+走平路的时间=15min.
设小华家到学校平路长xm,下坡长ym.
根据等量关系得
解这个方程组,得
因此,平路长为300m,下坡长为400m,小华家离学校700m.
【例3】某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.甲说:“我乘这种出租车走了11km,付了17元.”乙说:“我乘这种出租车走了23km,付了35元.”请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
即
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
【例4】某装订车间的工人要将一批书打包后送往邮局,其中每包书的数目相等.第一次它们领来这批书的 ,结果打了14个包还多35本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了11包.那么这批书共有多少本?
解 设这批书共有x本,每包书有y本.
根据等量关系,得
解这个方程组,得
答:这批书共有1500本.
练习
1.甲、乙两地相距360千米,一船往返鱼于甲、乙两地,顺流用了18小时,逆流用了24小时。若设船在静水中的速度为x千米/时,水流速度为y千米/时,可列方程组为
解:本问题涉及的等量关系有
(船在静水中的速度+水流速度)×18=360,
(船在静水中的速度-水流速度)×24=360.
根据等量关系,得
顺流
逆流
2.为了合理使用电力资源,缓解用电紧张状况,我国电力部门出台了使用“峰谷电”的政策及收费标准(如下表).已知王老师家4月份使用“峰谷电”95千瓦时,缴电费43.40元,问王老师家4月份“峰电”和“谷电”各用了多少千瓦时?
解:设王老师家4月份“峰电”用了x千瓦时,“谷电”用了y千瓦时.
根据等量关系,得
用电时间段 收费标准
峰电 8:00~22:00 0.56元/千瓦时
谷电 22:00~8:00 0.28元/千瓦时
解这个方程组,得
答:王老师家4月份“峰电”用了60千瓦时,“谷电”用了35千瓦时.
3.用一根绳子环绕一棵大树,若环绕大树3周,绳子还多4尺;若环绕大树4周,绳子又少了3尺,则这根绳子长多少尺?
解:设环绕大树一周需要x尺,这根绳子长y尺.
根据等量关系,得
解这个方程组,得
答:这根绳子长25尺.
课堂小结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
2.这种处理问题的过程可以进一步概括为:
第1章 有理数
1.3(第1课时) 二元一次方程组
的应用(1)
学习目标
1.会根据问题情境及条件列出二元一次方程组,解方 组,并检验解是否合理;(重点)
2.通过解决实际问题进一步体会方程建模的过程和作用.
3.寻找等量关系.(难点)
新课导入
动脑筋
“鸡兔同笼”是我国古代著名的数学趣题之一. 大约在1500年前成书的《孙子算经》中就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?” 这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有 35 个头;从下面数,有 94 条腿. 问笼中各有几只鸡和兔?
本题涉及的等量关系有:
鸡头数+兔头数=35,
鸡的腿数+兔子的腿数=94.
设鸡有x只,兔有y只.
根据等量关系,得
解这个方程组,得
答:笼中有23只鸡,12只兔.
【例1】某业余运动员针对自行车和长跑项目进行专项训练.某次训练中,他骑自行车的平均速度为10m/s,跑步的平均速度为 m/s,自行车路段和长跑路段共5km,共用时15min.求自行车路段和长跑路段的长度.
分析 本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
解 设自行车路段的长度为x m,长跑路段的长度为y m.
根据等量关系,得
解这个方程组,得
因此自行车路段长度为3000m,长跑路段的长度为2000m.
【例2】某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的甲乙两种配料. 用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克
分析 本问题涉及的等量关系有:
甲配料质量+乙配料质量=总质量,
甲配料含蛋白质质量+乙配料含蛋白质质量=总蛋白质质量.
解 设含蛋白质20%的配料需用x kg,含蛋白质12%的配料需用y kg.
根据等量关系,得
解这个方程组,得
答:可以配制出所要求的食品,其中含蛋白质20%的配料需用37.5kg,含蛋白质12%的配料需用62.5kg.
建立二元一次方程组解决实际问题的步骤如下:
实际问题
列二元一次方程组
解方程组
检验解是否符合实际情况
分析等量关系
设两个未知数
练习
1.植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵,求男生、女生各有多少人?
解:设男生有x人,女生有y人.
根据等量关系,得
解这个方程组,得
答:男生有12人,女生有8人.
2.某班去看演出,甲种票每张24元,乙种票每张18元,如果35名同学购票恰好用去750元,求甲、乙两种票各买了多少张?
解:设甲种票买了x张,乙种票买了y张.
根据等量关系,得
解这个方程组,得
答:甲种票买了20张,乙种票买了15张.
课堂小结
列方程组解决问题
关键:找等量关系
一般步骤:
审、设、列、解、验、答
第1章 有理数
1.3(第2课时) 二元一次方程组的应用(2)
学习目标
1.会根据问题情境及条件列出二元一次方程组,解方 组,并检验解是否合理;(重点)
2.通过解决实际问题进一步体会方程建模的过程和作用.
3.寻找等量关系.(难点)
新课导入
动脑筋
小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需要10min,从学校到家里需15min.问小华家离学校多远?
小华家到学校的路程分为两段:平路与坡路(回家所走的上坡路长即为去学校的下坡路长).根据问题中涉及的路程、速度与时间的数量关系,可得
从家到学校
从学校到家
走平路的时间+走下坡路的时间=10min,
走上坡路的时间+走平路的时间=15min.
设小华家到学校平路长xm,下坡长ym.
根据等量关系得
解这个方程组,得
因此,平路长为300m,下坡长为400m,小华家离学校700m.
【例3】某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.甲说:“我乘这种出租车走了11km,付了17元.”乙说:“我乘这种出租车走了23km,付了35元.”请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
即
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
【例4】某装订车间的工人要将一批书打包后送往邮局,其中每包书的数目相等.第一次它们领来这批书的 ,结果打了14个包还多35本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了11包.那么这批书共有多少本?
解 设这批书共有x本,每包书有y本.
根据等量关系,得
解这个方程组,得
答:这批书共有1500本.
练习
1.甲、乙两地相距360千米,一船往返鱼于甲、乙两地,顺流用了18小时,逆流用了24小时。若设船在静水中的速度为x千米/时,水流速度为y千米/时,可列方程组为
解:本问题涉及的等量关系有
(船在静水中的速度+水流速度)×18=360,
(船在静水中的速度-水流速度)×24=360.
根据等量关系,得
顺流
逆流
2.为了合理使用电力资源,缓解用电紧张状况,我国电力部门出台了使用“峰谷电”的政策及收费标准(如下表).已知王老师家4月份使用“峰谷电”95千瓦时,缴电费43.40元,问王老师家4月份“峰电”和“谷电”各用了多少千瓦时?
解:设王老师家4月份“峰电”用了x千瓦时,“谷电”用了y千瓦时.
根据等量关系,得
用电时间段 收费标准
峰电 8:00~22:00 0.56元/千瓦时
谷电 22:00~8:00 0.28元/千瓦时
解这个方程组,得
答:王老师家4月份“峰电”用了60千瓦时,“谷电”用了35千瓦时.
3.用一根绳子环绕一棵大树,若环绕大树3周,绳子还多4尺;若环绕大树4周,绳子又少了3尺,则这根绳子长多少尺?
解:设环绕大树一周需要x尺,这根绳子长y尺.
根据等量关系,得
解这个方程组,得
答:这根绳子长25尺.
课堂小结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
2.这种处理问题的过程可以进一步概括为:
