2.1.4 单项式与多项式相乘 课件 (共22张PPT) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 2.1.4 单项式与多项式相乘 课件 (共22张PPT) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 481.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 21:11:12 | ||
图片预览



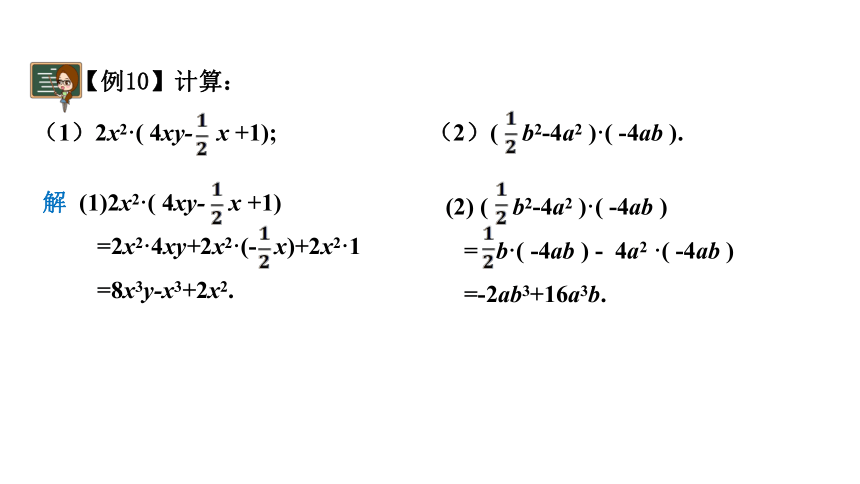


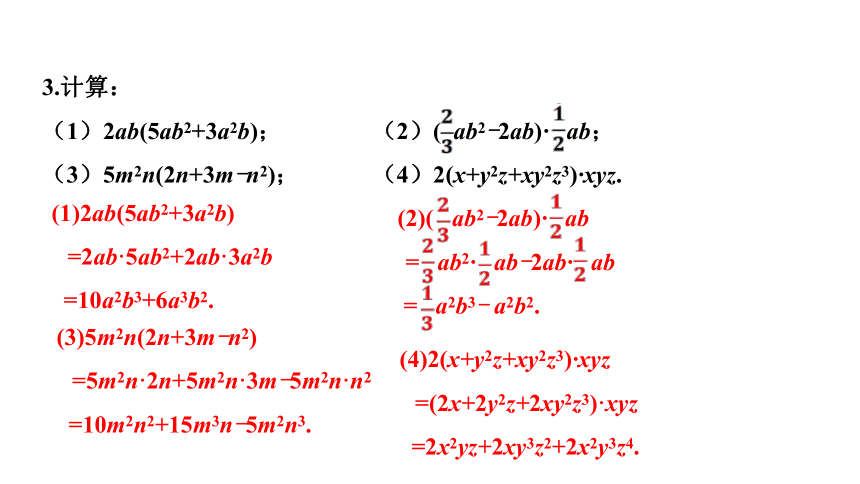


文档简介
(共22张PPT)
第2章 整式的乘法
2.1.4(第1课时) 单项式与多项式相乘
学习目标
能根据分配律和单项式与单项式相乘的法则探究得到单项式与多项式相乘的法则.(重、难点)
新课导入
动脑筋
怎样计算单项式2x与多项式3x2-x-5的积?
2x·(3x2-x-5)
= 2x·3x2+2x·(-x)+2x·(-5)
= 6x3-2x2-10x.
一般地,单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的每一项相加.
可以运用乘法对加法的分配律.
【例10】计算:
(1)2x2·( 4xy- x +1); (2)( b2-4a2 )·( -4ab ).
解 (1)2x2·( 4xy- x +1)
=2x2·4xy+2x2·(- x)+2x2·1
=8x3y-x3+2x2.
(2) ( b2-4a2 )·( -4ab )
= b·( -4ab ) - 4a2 ·( -4ab )
=-2ab3+16a3b.
【例11】求- x2·( 2xy-4y2)-4x2·( -xy)的值,其中x=2,y=-1.
解 - x2·( 2xy-4y2)-4x2·( -xy)
=( - x2)· 2xy- x2·( -4y2)-4x2·( -xy)
=-x3y+2x2y2+4x3y
=3x3y+2x2y2.
当x=2,y=-1时,
原式的值是3×23×(-1)+2×22×(-1)2=-24+8=-16.
先化简,再求值.
练习
1.计算-ab(2a2b-3ab2-4ab)的结果是( )
A.5a3b2 B.2a3b2-3a2b3-4a2b2 C.-2a3b2+3a2b3+4a2b2 D.-5a3b2
C
解析:-ab(2a2b-3ab2-4ab)
=-ab·2a2b+ab·3ab2+ab·4ab
=-2a3b2+3a2b3+4a2b2.
解析:3a·(2a2-3a-2)
=3a·2a2-3a·3a-3a·2
=6a3-6a2-6a.
2.3a·(2a2-3a-2)=
6a3-6a2-6a
3.计算:
(1)2ab(5ab2+3a2b); (2)( ab2-2ab)· ab;
(3)5m2n(2n+3m-n2); (4)2(x+y2z+xy2z3)·xyz.
(1)2ab(5ab2+3a2b)
=2ab·5ab2+2ab·3a2b
=10a2b3+6a3b2.
(2)( ab2-2ab)· ab
= ab2· ab-2ab· ab
= a2b3- a2b2.
(3)5m2n(2n+3m-n2)
=5m2n·2n+5m2n·3m-5m2n·n2
=10m2n2+15m3n-5m2n3.
(4)2(x+y2z+xy2z3)·xyz
=(2x+2y2z+2xy2z3)·xyz
=2x2yz+2xy3z2+2x2y3z4.
4.先化简,再求值:5a(2a2-5a+3)-2a2(5a+5)+7a2,其中a=2.
解析:5a(2a2-5a+3)-2a2(5a+5)+7a2
=5a·2a2-5a·5a+5a·3-2a2·5a-2a2·5+7a2
=10a3-25a2+15a-10a3-10a2+7a2
=-28a2+15a.
当a=2时,原式的值为 -28×22+15×2=-82.
课堂小结
单项式乘多项式的法则
(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
注意
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
第2章 整式的乘法
2.1.4(第2课时) 多项式与多项式相乘
学习目标
通过具体实例并结合单项式与多项式相乘的法则,总结多项式与多项式相乘的法则.(重、难点)
新课导入
动脑筋
有一套居室的平面图如图所示,怎样用代数表示它的总面积呢?
a
b
m
n
南北向总长为a+b,东西向总长为m+n,所以居室的总面积为: ( a+b )·( m+n ); ①
N
北边两间房的面积和为a(m+n),南边两间房的面积和为b(m+n),所以居室的总面积为:a( m+n )+b( m+n ); ②
四间房(厅)的面积分别为am,an,bm,bn,所以居室的总面积为:
am+an+bm+bn. ③
这三个代数式之间有什么关系呢?
上面三个代数式都正确表示了该居室的总面积,因此有:
( a+b )( m+n ) = a(m+n) +b( m+n ) = am+an+bm+bn.
撇开上述式子的实际意义,想一想,这几个代数式为什么相等呢?它们利用了乘法运算的什么性质?事实上,由代数式①到代数式②,是把m+n看成一个整体,利用乘法分配律得到a( m+n )+b( m+n ),继续利用乘法分配律,就得到结果am+an+bm+bn.这个运算过程可表示为:
( a+b )( m+n )=am+an+bm+bn.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
【例12】计算:
(1)(2x+y)( x-3y); (2)(2x+1)(x2-x-5); (3)(x+a)(x+b).
解 (1)(2x+y)( x-3y)
=2x·x+2x·(-3y)+y·x-y·(-3y)
=2x2-6xy+yx-3y2
=2x2-5xy-3y2.
(2) (2x+1)(x2-x-5)
=6x3 -2x2-10x+3x2-x-5
=6x3 +x2-11x-5.
(3)(x+a)(x+b)
=x2 +bx+ax+ab
=x2+(a+b)x+ab.
运算熟练后,第一步可以省略.
ax
ab
x2
bx
x
x
a
b
第(3)小题的直观意义如右图所示.
【例13】计算:
(1)( a+b )( a-b ); (2)( a+b )2; (3)( a-b )2.
解 (1)( a+b )( a-b )
=a2-ab+ba-b2
=a2-b2.
(2)( a+b )2
=( a+b )( a+b )
=a2+ab+ba+b2
=a2+2ab+b2.
(3)( a-b )2
=( a-b )( a-b )
=a2-ab-ba+b2
=a2-2ab+b2.
练习
1.计算:
(1)(x-2)(x+3); (2)(x+1)(x+5); (3)(x-3)2; (4)(m-2n)(2m+n).
(1)(x-2)(x+3)
=x2+3x-2x-6
=x2+x-6.
(2)(x+1)(x+5)
=x2+x+5x+5
=x2+6x+5.
(3)(x-3)2
=(x-3)·(x-3)
=x2-6x+9.
(4)(m-2n)(2m+n)
=m·2m+mn-2n·2m-2n·n
=2m2-3mn-2n2.
解析:(2x+3)(x+m)
=2x·x+2x·m+3x+3m
=2x2+(2m+3)x+3m.
2.若(2x+3)(x+m)=2x2+5x-n,则m= ,n= .
因为(2x+3)(x+m)=2x2+5x-n,
所以2x2+(2m+3)x+3m=2x2+5x-n,
所以 2m+3=5,所以 m=1,
3m=-n, n=-3.
1
-3
解析:(2m-3)(3m+4)
=2m·3m+2m·4-3·3m-3×4
=6m2-m-12.
当m=-3时,原式的值为
6×(-3)2-(-3)-12=45.
解析:(2x+5)(x+1)-(x-3)(x+1)
=2x·x+2x·1+5·x+5×1-(x·x+x·1-3·x-3×1)
=2x2+7x+5-(x2-2x-3)
=x2+9x+8.
当x=-7时,原式的值为(-7)2+9×(-7)+8=-6.
-6
3.(1)当m=-3时,(2m-3)(3m+4)的值是_______.
(2)当x=-7时,(2x+5)(x+1)-(x-3)(x+1)的值为_________.
45
4.计算:(a2+3)(a-2)-a(a2-2a-2).
解析: (a2+3)(a-2)-a(a2-2a-2)
=a3-2a2+3a-6-a3+2a2+2a
= 5a-6.
5.有一块长方形耕地,其中长为a,宽为b,现要在该耕地上种植两块防风带,如图所示的绿色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
A. bc-ab+ac+c2
B. ab-bc-ac+c2
C. a2+ab+bc-ac
D.b2-bc+a2-ab
c
a
b
c
解析:耕地面积为ab,横向防风带面积为ac,纵向防风带面积为bc,两者重合部分的面积为c2,所以剩余耕地的面积为ab-ac-bc+c2.
B
课堂小结
多项式乘多项式的法则
(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类 项之前),检验项数常常作为检验解题过程是否的有效方法;
(3)多项式与多项式相乘的结果中,要把同类项合并.
注意
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
第2章 整式的乘法
2.1.4(第1课时) 单项式与多项式相乘
学习目标
能根据分配律和单项式与单项式相乘的法则探究得到单项式与多项式相乘的法则.(重、难点)
新课导入
动脑筋
怎样计算单项式2x与多项式3x2-x-5的积?
2x·(3x2-x-5)
= 2x·3x2+2x·(-x)+2x·(-5)
= 6x3-2x2-10x.
一般地,单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的每一项相加.
可以运用乘法对加法的分配律.
【例10】计算:
(1)2x2·( 4xy- x +1); (2)( b2-4a2 )·( -4ab ).
解 (1)2x2·( 4xy- x +1)
=2x2·4xy+2x2·(- x)+2x2·1
=8x3y-x3+2x2.
(2) ( b2-4a2 )·( -4ab )
= b·( -4ab ) - 4a2 ·( -4ab )
=-2ab3+16a3b.
【例11】求- x2·( 2xy-4y2)-4x2·( -xy)的值,其中x=2,y=-1.
解 - x2·( 2xy-4y2)-4x2·( -xy)
=( - x2)· 2xy- x2·( -4y2)-4x2·( -xy)
=-x3y+2x2y2+4x3y
=3x3y+2x2y2.
当x=2,y=-1时,
原式的值是3×23×(-1)+2×22×(-1)2=-24+8=-16.
先化简,再求值.
练习
1.计算-ab(2a2b-3ab2-4ab)的结果是( )
A.5a3b2 B.2a3b2-3a2b3-4a2b2 C.-2a3b2+3a2b3+4a2b2 D.-5a3b2
C
解析:-ab(2a2b-3ab2-4ab)
=-ab·2a2b+ab·3ab2+ab·4ab
=-2a3b2+3a2b3+4a2b2.
解析:3a·(2a2-3a-2)
=3a·2a2-3a·3a-3a·2
=6a3-6a2-6a.
2.3a·(2a2-3a-2)=
6a3-6a2-6a
3.计算:
(1)2ab(5ab2+3a2b); (2)( ab2-2ab)· ab;
(3)5m2n(2n+3m-n2); (4)2(x+y2z+xy2z3)·xyz.
(1)2ab(5ab2+3a2b)
=2ab·5ab2+2ab·3a2b
=10a2b3+6a3b2.
(2)( ab2-2ab)· ab
= ab2· ab-2ab· ab
= a2b3- a2b2.
(3)5m2n(2n+3m-n2)
=5m2n·2n+5m2n·3m-5m2n·n2
=10m2n2+15m3n-5m2n3.
(4)2(x+y2z+xy2z3)·xyz
=(2x+2y2z+2xy2z3)·xyz
=2x2yz+2xy3z2+2x2y3z4.
4.先化简,再求值:5a(2a2-5a+3)-2a2(5a+5)+7a2,其中a=2.
解析:5a(2a2-5a+3)-2a2(5a+5)+7a2
=5a·2a2-5a·5a+5a·3-2a2·5a-2a2·5+7a2
=10a3-25a2+15a-10a3-10a2+7a2
=-28a2+15a.
当a=2时,原式的值为 -28×22+15×2=-82.
课堂小结
单项式乘多项式的法则
(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
注意
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
第2章 整式的乘法
2.1.4(第2课时) 多项式与多项式相乘
学习目标
通过具体实例并结合单项式与多项式相乘的法则,总结多项式与多项式相乘的法则.(重、难点)
新课导入
动脑筋
有一套居室的平面图如图所示,怎样用代数表示它的总面积呢?
a
b
m
n
南北向总长为a+b,东西向总长为m+n,所以居室的总面积为: ( a+b )·( m+n ); ①
N
北边两间房的面积和为a(m+n),南边两间房的面积和为b(m+n),所以居室的总面积为:a( m+n )+b( m+n ); ②
四间房(厅)的面积分别为am,an,bm,bn,所以居室的总面积为:
am+an+bm+bn. ③
这三个代数式之间有什么关系呢?
上面三个代数式都正确表示了该居室的总面积,因此有:
( a+b )( m+n ) = a(m+n) +b( m+n ) = am+an+bm+bn.
撇开上述式子的实际意义,想一想,这几个代数式为什么相等呢?它们利用了乘法运算的什么性质?事实上,由代数式①到代数式②,是把m+n看成一个整体,利用乘法分配律得到a( m+n )+b( m+n ),继续利用乘法分配律,就得到结果am+an+bm+bn.这个运算过程可表示为:
( a+b )( m+n )=am+an+bm+bn.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
【例12】计算:
(1)(2x+y)( x-3y); (2)(2x+1)(x2-x-5); (3)(x+a)(x+b).
解 (1)(2x+y)( x-3y)
=2x·x+2x·(-3y)+y·x-y·(-3y)
=2x2-6xy+yx-3y2
=2x2-5xy-3y2.
(2) (2x+1)(x2-x-5)
=6x3 -2x2-10x+3x2-x-5
=6x3 +x2-11x-5.
(3)(x+a)(x+b)
=x2 +bx+ax+ab
=x2+(a+b)x+ab.
运算熟练后,第一步可以省略.
ax
ab
x2
bx
x
x
a
b
第(3)小题的直观意义如右图所示.
【例13】计算:
(1)( a+b )( a-b ); (2)( a+b )2; (3)( a-b )2.
解 (1)( a+b )( a-b )
=a2-ab+ba-b2
=a2-b2.
(2)( a+b )2
=( a+b )( a+b )
=a2+ab+ba+b2
=a2+2ab+b2.
(3)( a-b )2
=( a-b )( a-b )
=a2-ab-ba+b2
=a2-2ab+b2.
练习
1.计算:
(1)(x-2)(x+3); (2)(x+1)(x+5); (3)(x-3)2; (4)(m-2n)(2m+n).
(1)(x-2)(x+3)
=x2+3x-2x-6
=x2+x-6.
(2)(x+1)(x+5)
=x2+x+5x+5
=x2+6x+5.
(3)(x-3)2
=(x-3)·(x-3)
=x2-6x+9.
(4)(m-2n)(2m+n)
=m·2m+mn-2n·2m-2n·n
=2m2-3mn-2n2.
解析:(2x+3)(x+m)
=2x·x+2x·m+3x+3m
=2x2+(2m+3)x+3m.
2.若(2x+3)(x+m)=2x2+5x-n,则m= ,n= .
因为(2x+3)(x+m)=2x2+5x-n,
所以2x2+(2m+3)x+3m=2x2+5x-n,
所以 2m+3=5,所以 m=1,
3m=-n, n=-3.
1
-3
解析:(2m-3)(3m+4)
=2m·3m+2m·4-3·3m-3×4
=6m2-m-12.
当m=-3时,原式的值为
6×(-3)2-(-3)-12=45.
解析:(2x+5)(x+1)-(x-3)(x+1)
=2x·x+2x·1+5·x+5×1-(x·x+x·1-3·x-3×1)
=2x2+7x+5-(x2-2x-3)
=x2+9x+8.
当x=-7时,原式的值为(-7)2+9×(-7)+8=-6.
-6
3.(1)当m=-3时,(2m-3)(3m+4)的值是_______.
(2)当x=-7时,(2x+5)(x+1)-(x-3)(x+1)的值为_________.
45
4.计算:(a2+3)(a-2)-a(a2-2a-2).
解析: (a2+3)(a-2)-a(a2-2a-2)
=a3-2a2+3a-6-a3+2a2+2a
= 5a-6.
5.有一块长方形耕地,其中长为a,宽为b,现要在该耕地上种植两块防风带,如图所示的绿色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
A. bc-ab+ac+c2
B. ab-bc-ac+c2
C. a2+ab+bc-ac
D.b2-bc+a2-ab
c
a
b
c
解析:耕地面积为ab,横向防风带面积为ac,纵向防风带面积为bc,两者重合部分的面积为c2,所以剩余耕地的面积为ab-ac-bc+c2.
B
课堂小结
多项式乘多项式的法则
(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类 项之前),检验项数常常作为检验解题过程是否的有效方法;
(3)多项式与多项式相乘的结果中,要把同类项合并.
注意
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
