2.2.2 完全平方公式 课件 (共18张PPT) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 2.2.2 完全平方公式 课件 (共18张PPT) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 323.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 21:13:05 | ||
图片预览






文档简介
第2章 整式的乘法
2.2.2(第1课时) 完全平方公式
学习目标
1.能根据多项式的乘法发现规律,进一步归纳出完全平方公式,了解公式的几何背景,并能进行简单的计算;
2.掌握完全平方公式的结构特征,理解公式中字母的含义,并能正确的运用公式.(重、难点)
新课导入
动脑筋
计算下列各式,你能发现什么规律:
( a+1 )2=( a+1 )( a+1 )=a2+a+a+12=a2+2·a·1+12,
( a+2 )2=( a+2 )( a+2 )=a2+2a+2a+22=a2+2·a·2+22,
( a+3 )2=( a+3 )( a+3 )=a2+3a+3a+32=a2+2·a·3+32,
( a+4 )2=( a+4 )( a+4 )=a2+4a+4a+42=a2+2·a·4+42.
我们用多项式乘法来推导一般情况
( a+b )2=( a+b )( a-b )
=a2+ab+ab+b2
=a2+2ab+b2.
做一做
( a-b )2= ?
把( a+b )2=a2+2ab+b2中的“b”换做“-b”,试试看.
( a-b )2=[a+( -b )]2=a2+2a( -b )+( -b )2
=a2-2ab+b2.
我们把
( a+b )2=a2+2ab+b2,( a-b )2=a2-2ab+b2.
都叫做完全平方公式.即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.
说一说
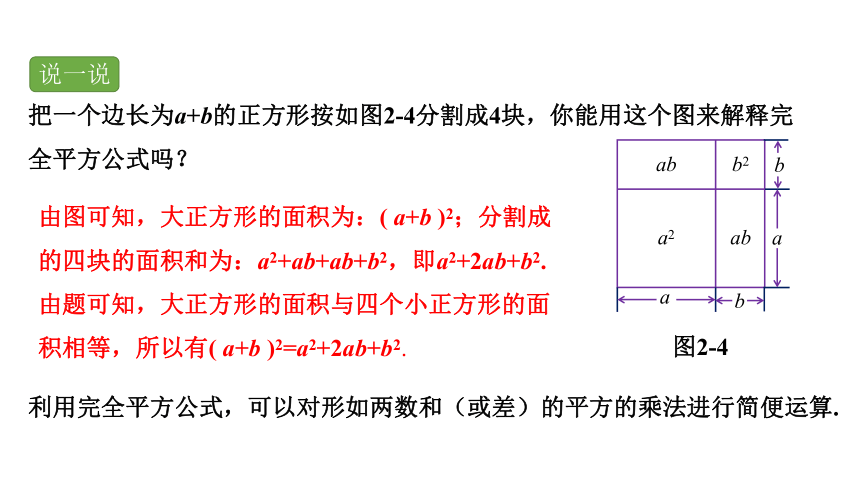
把一个边长为a+b的正方形按如图2-4分割成4块,你能用这个图来解释完全平方公式吗?
图2-4
由图可知,大正方形的面积为:( a+b )2;分割成的四块的面积和为:a2+ab+ab+b2,即a2+2ab+b2.由题可知,大正方形的面积与四个小正方形的面积相等,所以有( a+b )2=a2+2ab+b2.
利用完全平方公式,可以对形如两数和(或差)的平方的乘法进行简便运算.
ab
ab
a2
b2
a
b
a
b
【例4】运用完全平方公式计算:
(1)( 3m+n )2; (2)( x- y ).
解 (1)( 3m+n )2
=( 3m )2+2·3m·n+n2
=9m2+6mn+n2.
(2)( x- y )
=x2- 2·x· +( )2
=x2-x+ .
把“3m”看成完全平方公式中的“a”.
练习
1.下面各式的计算对不对?如果不对,应怎样改正?
(1)(x -y)2 =x2 -y2; (2)(x+y)2 = x2+xy+y2.
解 (1)不对 (x -y)2=x2 -2xy+y2.
(2)不对 (x +y)2=x2 +2xy+y2.
2.若x+mx+16=(x+n)2,其中m、n为常数,则n的值是( )
A.n=8 B.n= C.n=4 D.n=
解析: 令m=8,则x+mx+16可以写成(x+4)2,所以n=4;
令m=-8,则x+mx+16可以写成(x-4)2,所以n=-4.
综上,n= .
3.已知a2+b2=12,ab=-3,则(a+b)2的值是( )
A. 3 B. 6 C. 12 D. 18
解析:因为(a+b)2
=a2+2ab+b2
=a2+b2+2ab.
所以(a+b)2 =12+2×(-3)=6.
解析:因为a=b+3,
所以a-b=3,
所以a2-2ab+b2=(a-b)2=32=9.
B
4.若a=b+3,则a2-2ab+b2的值是( )
A. 3 B. 6 C. 9 D. 12
C
课堂小结
a2 +b2=(a+b)2- 2ab
=(a-b)2+ 2ab
4ab=(a+b)2-(a-b)2
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1.完全平方公式:
2.注意:项数、符号、字母及其指数;
3.解题时常用结论:
第2章 整式的乘法
2.2.2(第2课时) 完全平方公式的运用
学习目标
掌握完全平方公式的结构特征,理解公式中字母的含义,并能正确的运用公式.(重、难点)
新课导入
说一说
( a-b )2与( b-a )2,( a+b )2与( -a-b )2相等吗?为什么?
相等.
因为( b-a )2=[-( a-b )]2=( a-b )2,所以( a-b )2=( b-a )2;
又因为( -a-b )2=[-( a+b )]2=( a+b )2,所以( a+b )2=( -a-b )2.
用完全平方公式将它们分别展开,也可得到相等.
【例5】运用完全平方公式计算:
(1)( -x+1 )2; (2)( -2x-3 )2.
解 (1)( -x+1 )2
=( -x )2+2( -x )·1+12
=x2-2x+1.
(2)( -2x-3 )2.
=[-( 2x+3 )]2.
=( 2x+3 )2.
=4x2+12x+9.
第(1)题这样做,对吗?
( -x+1 )2
=( 1-x )2
=12-2·1·x+x2
=1-2x+x2.
【例6】计算:
(1)( a+b )2-( a-b )2; (2)( a+b+1 )2.
解 (1)( a+b )2-( a-b )2
=a2+2ab+b2-( a2-2ab+b2 )
=a2+2ab+b2- a2+2ab-b2 )
=4ab.
(2)( a+b+1 )2
=[( a+b)+1 ]2
=( a+b )2+2( a+b )+1
=a2+2ab+b2+2a+2b+1.
【例7】计算:
(1)1042; (2)1982.
解 (1)1042=( 100+4 )2
=1002+2×100×4+42
=10000+800+16
=10816.
(2)1982=( 200-2 )2
=2002-2×200×2+22
=40000-800+4
=39204.
运用完全平方公式可以简化一些运算.
练习
1.已知 (m-n)2=8,(m+n)2=2,则m2+n2=( )
A. 10 B. 6 C. 5 D. 3
解析:因为 (m-n)2=8,所以m2-2mn+n2=8①,因为(m+n)2=2,
所以m2+2mn+n2=2②,①+②,得2m2+2n2=10,所以m2+n2=5.
2.已知xy=5,x+y=6,则x-y= .
解析: 因为(x+y)2=x2+2xy+y2=36,xy=5,所以x2+y2=26;
因为(x-y)2=x2-2xy+y2=26-2×5=16,所以x-y=4.
C
4
3.已知a+b=3,ab=-12,求下列各式的值.
(1)a2+b2, (2)a2-ab+b2.
解:(1)a2+b2
=(a+b)2 -2ab
=32-2×(-12)
=33.
(2)a2-ab+b2
=a2+b2-ab
=33-(-12)
=45.
解:(1)10022=( 100+2 )2
=1002+2×100×2+22
=10000+400+4
=10404.
4.计算:
(1)10022; (2)992.
(2)992=( 100-1 )2
=1002-2×100×1+12
=10000-200+1
=9801.
在解题过程中要准确确定a和b,对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键.
课堂小结
(a±b)2= a2 ±2ab+b2
法则
运用
完全平方公式
2.2.2(第1课时) 完全平方公式
学习目标
1.能根据多项式的乘法发现规律,进一步归纳出完全平方公式,了解公式的几何背景,并能进行简单的计算;
2.掌握完全平方公式的结构特征,理解公式中字母的含义,并能正确的运用公式.(重、难点)
新课导入
动脑筋
计算下列各式,你能发现什么规律:
( a+1 )2=( a+1 )( a+1 )=a2+a+a+12=a2+2·a·1+12,
( a+2 )2=( a+2 )( a+2 )=a2+2a+2a+22=a2+2·a·2+22,
( a+3 )2=( a+3 )( a+3 )=a2+3a+3a+32=a2+2·a·3+32,
( a+4 )2=( a+4 )( a+4 )=a2+4a+4a+42=a2+2·a·4+42.
我们用多项式乘法来推导一般情况
( a+b )2=( a+b )( a-b )
=a2+ab+ab+b2
=a2+2ab+b2.
做一做
( a-b )2= ?
把( a+b )2=a2+2ab+b2中的“b”换做“-b”,试试看.
( a-b )2=[a+( -b )]2=a2+2a( -b )+( -b )2
=a2-2ab+b2.
我们把
( a+b )2=a2+2ab+b2,( a-b )2=a2-2ab+b2.
都叫做完全平方公式.即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.
说一说
把一个边长为a+b的正方形按如图2-4分割成4块,你能用这个图来解释完全平方公式吗?
图2-4
由图可知,大正方形的面积为:( a+b )2;分割成的四块的面积和为:a2+ab+ab+b2,即a2+2ab+b2.由题可知,大正方形的面积与四个小正方形的面积相等,所以有( a+b )2=a2+2ab+b2.
利用完全平方公式,可以对形如两数和(或差)的平方的乘法进行简便运算.
ab
ab
a2
b2
a
b
a
b
【例4】运用完全平方公式计算:
(1)( 3m+n )2; (2)( x- y ).
解 (1)( 3m+n )2
=( 3m )2+2·3m·n+n2
=9m2+6mn+n2.
(2)( x- y )
=x2- 2·x· +( )2
=x2-x+ .
把“3m”看成完全平方公式中的“a”.
练习
1.下面各式的计算对不对?如果不对,应怎样改正?
(1)(x -y)2 =x2 -y2; (2)(x+y)2 = x2+xy+y2.
解 (1)不对 (x -y)2=x2 -2xy+y2.
(2)不对 (x +y)2=x2 +2xy+y2.
2.若x+mx+16=(x+n)2,其中m、n为常数,则n的值是( )
A.n=8 B.n= C.n=4 D.n=
解析: 令m=8,则x+mx+16可以写成(x+4)2,所以n=4;
令m=-8,则x+mx+16可以写成(x-4)2,所以n=-4.
综上,n= .
3.已知a2+b2=12,ab=-3,则(a+b)2的值是( )
A. 3 B. 6 C. 12 D. 18
解析:因为(a+b)2
=a2+2ab+b2
=a2+b2+2ab.
所以(a+b)2 =12+2×(-3)=6.
解析:因为a=b+3,
所以a-b=3,
所以a2-2ab+b2=(a-b)2=32=9.
B
4.若a=b+3,则a2-2ab+b2的值是( )
A. 3 B. 6 C. 9 D. 12
C
课堂小结
a2 +b2=(a+b)2- 2ab
=(a-b)2+ 2ab
4ab=(a+b)2-(a-b)2
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1.完全平方公式:
2.注意:项数、符号、字母及其指数;
3.解题时常用结论:
第2章 整式的乘法
2.2.2(第2课时) 完全平方公式的运用
学习目标
掌握完全平方公式的结构特征,理解公式中字母的含义,并能正确的运用公式.(重、难点)
新课导入
说一说
( a-b )2与( b-a )2,( a+b )2与( -a-b )2相等吗?为什么?
相等.
因为( b-a )2=[-( a-b )]2=( a-b )2,所以( a-b )2=( b-a )2;
又因为( -a-b )2=[-( a+b )]2=( a+b )2,所以( a+b )2=( -a-b )2.
用完全平方公式将它们分别展开,也可得到相等.
【例5】运用完全平方公式计算:
(1)( -x+1 )2; (2)( -2x-3 )2.
解 (1)( -x+1 )2
=( -x )2+2( -x )·1+12
=x2-2x+1.
(2)( -2x-3 )2.
=[-( 2x+3 )]2.
=( 2x+3 )2.
=4x2+12x+9.
第(1)题这样做,对吗?
( -x+1 )2
=( 1-x )2
=12-2·1·x+x2
=1-2x+x2.
【例6】计算:
(1)( a+b )2-( a-b )2; (2)( a+b+1 )2.
解 (1)( a+b )2-( a-b )2
=a2+2ab+b2-( a2-2ab+b2 )
=a2+2ab+b2- a2+2ab-b2 )
=4ab.
(2)( a+b+1 )2
=[( a+b)+1 ]2
=( a+b )2+2( a+b )+1
=a2+2ab+b2+2a+2b+1.
【例7】计算:
(1)1042; (2)1982.
解 (1)1042=( 100+4 )2
=1002+2×100×4+42
=10000+800+16
=10816.
(2)1982=( 200-2 )2
=2002-2×200×2+22
=40000-800+4
=39204.
运用完全平方公式可以简化一些运算.
练习
1.已知 (m-n)2=8,(m+n)2=2,则m2+n2=( )
A. 10 B. 6 C. 5 D. 3
解析:因为 (m-n)2=8,所以m2-2mn+n2=8①,因为(m+n)2=2,
所以m2+2mn+n2=2②,①+②,得2m2+2n2=10,所以m2+n2=5.
2.已知xy=5,x+y=6,则x-y= .
解析: 因为(x+y)2=x2+2xy+y2=36,xy=5,所以x2+y2=26;
因为(x-y)2=x2-2xy+y2=26-2×5=16,所以x-y=4.
C
4
3.已知a+b=3,ab=-12,求下列各式的值.
(1)a2+b2, (2)a2-ab+b2.
解:(1)a2+b2
=(a+b)2 -2ab
=32-2×(-12)
=33.
(2)a2-ab+b2
=a2+b2-ab
=33-(-12)
=45.
解:(1)10022=( 100+2 )2
=1002+2×100×2+22
=10000+400+4
=10404.
4.计算:
(1)10022; (2)992.
(2)992=( 100-1 )2
=1002-2×100×1+12
=10000-200+1
=9801.
在解题过程中要准确确定a和b,对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键.
课堂小结
(a±b)2= a2 ±2ab+b2
法则
运用
完全平方公式
